一種改進鯨魚算法及其在短時交通流預測中的應用研究

胡 松，成 衛，李 艾

1(昆明理工大學 交通工程學院 ，昆明 650500)

2(玉溪市公安局交通警察支隊，云南 玉溪 653100)

1 引 言

群智能算法是對自然環境中一些生物的群體行為特征進行模擬而得出的一類算法，如觀察鳥類捕食方式模擬出的粒子群算法，根據生物進化得到的遺傳算法[1]等在現在的眾多領域如電力調度、資源配置、計算機應用、醫學分析等有著廣泛應用.鯨魚優化算法(Whale Optimization Algorithm,WOA)[2]在2016年由澳大利亞學者Mirjalili通過對座頭鯨覓食行為的研究，得到的一種新的群智能算法，WOA主要是模擬鯨魚在捕獵過程中的靠近獵物的行為，從而找到復雜尋優問題的最優解.標準WOA具有參數少，全局收斂性好等優點，因此大量學者開始將該算法用于實際應用當中.如D.B.Prakash[3]等將WOA應用于徑向網絡中電容的選址問題，證明了WOA在維持電壓的穩定性和優化運行成本上的優越性.Pradeep Jangir[4]等使用WOA訓練多層感知器，解決了局部最優問題，獲得了較高的尋優精度；但是同傳統的群智能算法一樣容易陷入局部極值及收斂速率慢這些問題，學者們提出了一些改進的方法,例如閆旭[5]等將量子算法加入WOA中并用來解決TSP問題;郭振洲[6]等使用自適應權重和柯西變異改進WOA.

在以前學者的研究基礎上，本文針對WOA前期收斂速度較慢以及容易陷入局部最優解的問題，提出一種基于自適應權重和天牛須搜索[7，8](Beetle Antennae Search,BAS)的鯨魚優化算法.改進的算法通過將鯨魚優化算法中的搜索捕食策略使用天牛須搜索策略代替，加快前期的搜索能力和提升搜索精度；同時在包圍捕食和氣泡網攻擊中引入了自適應權重增強后期的局部搜索能力，通過測試函數仿真表明，改進后的自適應天牛須鯨魚混合優化算法(ABOA)相較于粒子群算法(PSO)、遺傳算法(GA)以及標準鯨魚優化算法(WOA)在收斂速度及收斂精度上有了明顯提升.

智能交通系統被認為是緩解道路擁堵，加強交通安全，促進節能減排的有效方法之一，可以幫助出行者帶來實時有效的交通信息從而在交通路徑選擇上作出更有效的判斷，緩解城市交通壓力，提高出行者的出行效率.隨著海量的交通數據被人們獲取，短時交通流的預測也變得越來越可靠，對智能交通系統的幫助也日益增大.在交通流預測上前人已經有了大量的研究，錢偉[9]使用相空間重構優化Kalman濾波進行短時交通流預測，解決了Kalman濾波模型時間滯后性的問題；Kumar[10]把季節性的影響結合進了車流的變化中，提出了一種基于季節的SARIMA模型，將原本的ARIMA模型進行預測時的適用范圍進行了擴大；Wu[11]等使用改進K-近鄰預測模型對短時交通流作出了預測，并在不同時間點和條件下驗證了其預測的適用性.傅貴等[12]引入核函數，把屬于非線性回歸的短時交通流預測問題轉化為Hilbert空間中的線性回歸問題，建立了基于SVMR的短時交通流預測模型.LSSVM是SVM的改進，可以有效地對處理非線性數據，并且其訓練時間短，適用性強.王賀[13]等使用聚類經驗模態分解和LSSVM組合進行短時風能預測；Liu[14]等使用改進的GSA算法優化LSSVM構建汽輪機熱耗率預測模型，并證明了其有效性；Sun[15]等使用LSSVM進行了PM2.5濃度預測.LSSVM進行回歸預測時主要依賴參數選擇，直接影響模型的性能.前人已有使用粒子群算法，遺傳算法等進行參數尋優[16,17]，并取得了較好的效果.文中采用改進的WOA算法將LSSVM中的兩個參數(核函數參數和懲罰系數)進行自動搜索確定,得到了一種ABOA-LSSVM短期交通流預測模型，并進行了實驗驗證其有效性.

2 鯨魚優化算法

鯨魚優化算法具有原理簡單、操作簡易，易于實現，需調整的參數少及魯棒性強等特點.在函數優化方面，WOA算法在求解精度和穩定性上要明顯優于粒子群(PSO)、差分進(DE)和引力搜索(GSA)等算法.通過模擬座頭鯨的捕食獵物的過程中的一系列行為，從而獲得優化的數學模型，從而完成的算法.該算法主要包含有3個階段：包圍獵物(encircling prey)、氣泡網攻擊(bubble-net attacking)、搜尋獵物(search for prey)3種方式.下面是3種方式的簡單介紹.

2.1 包圍獵物階段

在鯨魚捕食開始時，算法假設當前的最優捕食個體的位置是最佳捕食位置，然后剩余個體朝著最有位置靠攏，其數學模型表示為:

(1)

(2)

式中:A和C為系數向量;X*(t)為當前最佳個體位置，X(t)表示當前個體位置，t表示迭代次數.系數向量A和C用來控制鯨魚的游走方式，計算公式如下:

(3)

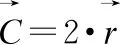
(4)

2.2 氣泡網攻擊階段

在WOA算法中，群體中個體的位置更新方式是根據生成使得隨機數的取值來在螺旋式位置更新和縮小包圍范圍(shrinking en-circling mechanism)這兩種更新方式中選取.

1)收縮包圍 即減少式(3)中的a值.在這個過程中，A在區間[-a，a]內進行取值，如果這個區間范圍發生改變，那么a的值也會隨之發生變化，若A在區間[-1，1]內進行取值，則鯨魚的游動位置將處于當前位置和獵物位置中間某個位置，這種方式體現出了鯨魚個體的局部搜索能力.包圍過程根據式(1)進行更新.

2)螺旋式位置更新 即鯨魚個體通過螺旋形的運動方式靠近群體中的最優位置，螺旋式位置更新的數學模型表示如下:

(5)

(6)

式中:D′為第i頭鯨魚當下位置與當前最佳個體間的間距，參數b則表示一個定義對數螺旋形狀的常數;l是[-1，1]上的隨機數.座頭鯨在圍捕獵物時一邊以螺旋形態游向獵物一邊縮小包圍圈，以0.5作為臨界值進行自身位置的更新.更新位置的公式為:

(7)

式中p為[0,1]區間上的隨機數.

2.3 搜索捕食

除使用氣泡網法搜索策略以外，鯨魚個體還能夠隨機游走搜索獵物，更新時依據系數A的變換進行選擇.式(8)、式(9)表示當|A|不小于1時，鯨魚個體隨機向別的鯨魚靠攏，距離值D則隨機更新，從而擴大搜索范圍，使捕食能力提升，這樣WOA就擁有一定程度的全局搜索能力.數學模型表示如下:

(8)

(9)

3 鯨魚群優化算法的改進

本文將WOA與天牛須搜索算法結合在一起，將WOA的隨機搜索行為用天牛須搜索來代替，加快算法的前期收斂效率，并保證WOA的遍歷性增強算法的全局搜索能力，避免陷入局部最優.加上自適應權重使得算法在后期的局部搜索時提高搜索精度，保證算法后期的收斂精度.

3.1 自適應權重

WOA實現局部尋優的操作是按照公式(2)和公式(5)進行局部搜索的，這時當鯨魚按照公式(2)朝著局部最優解逼近時，這時只能逼近局部最優解，而不能進行更好的局部尋優，如果當鯨魚接近食物的時候，采用較小的自適應權重改變此時最優的鯨魚的位置，則會提升WOA的局部尋優能力.自適應權值公式如(10)所示；改進后的自適應更新公式如(11)所示:

(10)

(11)

式中，t表示當前迭代次數，而T表示最大迭代次數.

3.2 天牛須搜索策略

天牛須搜索算法(BAS)是2017年由研究人員通過觀察天牛覓食的行為而得到的智能算法,它是根據天牛左右觸角接受到的食物氣味濃度的差別來決定位置更新的方向，從而到達食物位置.天牛須搜索算法屬于個體智能算法，只需要一個個體，算法的運算速度快,算法個體的位置定義如式(12)、式(13)所示.

1)天牛的朝向是隨機的，通過以下公式定義為:

(12)

2)天牛左右須的空間坐標按如下所示創建:

(13)

式中：t是算法循環次數；d是天牛左右須間的距離.

3)天牛的位置按照以下公式更新:

x(t+1)=x(t)+σtbsign[fr-fl]

(14)

式中，fr和fl表示的是適應度；σt表示在第t次更新時的距離；sign()表示符號函數.在進行尋優時使用δt=αδt-1，其中α為步長因子，通常設成0.95，這樣可以通過α來逐漸減小更新時的步長，能大大提升BAS算法的尋優能力及收斂速率.

改進算法的主要步驟如下:

步驟1.初始化.設置鯨魚群的種群大小、鯨魚優化算法迭代的次數以及天牛須算法步長等參數.

步驟2.設定鯨魚群的迭代次數t=0，比較初始種群中全部個體的適應度值，將鯨魚群中適應度值最好的個體所代表的狀態記錄到公告板中，記錄最好的適應度值.

步驟3.將迭代次數加1，對每一個個體下一步的的位置進行評價，根據評價選擇下一步所要執行的操作，包括：收縮包圍，螺旋位置更新或者隨機位置更新.將算法中的隨機位置更新方式用天牛須搜索算法代替，即將式(9)使用式(14)代替進行一次天牛須算法尋優，然后則將最優適應度的值輸出.當評價完3種行為得到的適應度之后，將適應度值進行比較，從而選取鯨魚個體的下一步位置.同時將更新后的鯨魚群中的最好適應度與公告板中記錄的最好適應度進行對比，及時更新公告板.

步驟4.判斷混合算法的迭代次數是否已經達上限，若沒達到則返回步驟3，如果滿足則選取適應度值最好的個體進行輸出.

4 算法的實例測試與分析

本文通過對選取的18個不同類型的基準測試函數進行仿真實驗來驗證ABOA算法的尋優能力.表1-表3給出了18個基準測試函數的詳細相關信息.其中，F1-F7選取的是單峰函數，F8-F12選取的是多峰函數，F13-F18為固定維函數.函數仿真實驗結果與分析

表1 單峰函數

表2 多峰函數

表3 固定維函數

將ABOA算法與PSO算法、GA算法以及WOA算法進行對比試驗,每種算法進行50次實驗，把50次尋優的結果取平均值以及計算最優解的標準差放在表4中(表中部分數據來自文獻[4,8]).

根據對單峰、多峰、固定維函數的測試比較，從表4可以看出ABOA在函數F1、F3、F9、F11、F17都收斂到了最小值，而且標準差為0或者接近0；在測試函數F2、F4、F7、F10迭代結束后沒有收斂到最優解，但是在收斂精度上，穩定性上都優于其他3種算法；F5的求解精度優于GA,PSO算法，相對WOA算法略差；對函數F6的求解精度僅次于PSO算法；對函數F14的求解精度僅次于GA算法；對F15，F16、F18來說和其它3種算法相比，優化前后差距不明顯;僅對F8進行優化時結果相對較差.整體上來說，ABOA在收斂精度和穩定性上都有提升，特別是在單峰和多峰函數，其全局尋優能力明顯較強.本文選取了4個函數的迭代進化圖，來直觀的展示函數的優化效果對比，可以看出ABOA算法在收斂精度及收斂速率上都占優，如圖1～圖4所示.

表4 測試結果

圖1 F1迭代圖

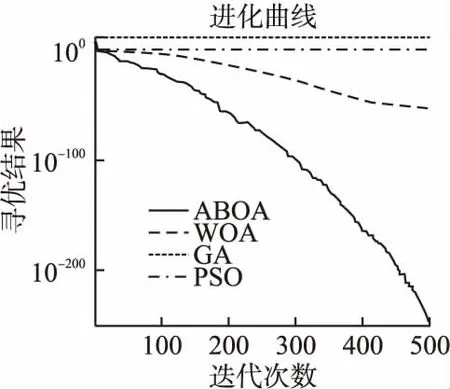
圖2 F2迭代圖

圖3 F9迭代圖

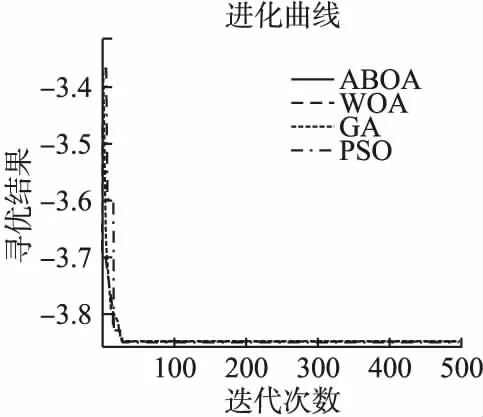
圖4 F18迭代圖

5 最小二乘支持向量機模型

最小二乘支持相機模型是對支持向量機的一種改進，通過把SVM不等式約束變為等式約束來降低求解二次規劃問題時的計算難度，該模型算法在進行非線性問題求解方面十分有效，而短時交通流預測就是要在復雜的交通系統中進行非線性求解，因此本文選取LSSVM進行短時交通流預測，該模型對短時交通流進行預測的基本描述如下.給定訓練樣本數據集:

S={(xi,yi),xi∈Rn,yi∈R},i=1,2,…,l

(15)

式中：xi表示與交通預測模型的預測量密切相關的一些影響因素，如交通流量，道路占有率等，n表示輸入數據的維數；yi為短時交通流預測的期望值；l為獲取的歷史樣本個數.由于道路上的流量是根據時間序列變化的，所以當前的交通流量與前一段時間的交通流量存在著關聯性.因此，前面一段時間的流量序列數據可以用來預測未來的交通流.通常把輸入的交通參數xi與輸出的交通流y二者的非線性關系轉變成φ(x)與y之間的線性關系,非線性短時交通流預測的決策函數可以定義為:

f(x)=(ω,φ(x))+b

(16)

其中，φ(x)是LSSVM的核函數，可以將輸入的歷史流量數據映射到更高維的空間進行求解.b為偏差量，ω為權值向量.使用LSSVM的優化函數對目標函數值進行優化可轉化為：

(17)

式中：ei表示真實值與預測值二者的擬合誤差,γ為LSSVM模型的懲罰因子，用來控制誤差的懲罰力度大小及調整模型復雜度，加上拉格朗日乘子αi并構造拉格朗日函數進行求解如下:

(18)

根據KKT條件得:

(19)

消去ω和ei，并且改寫成矩陣形式為:

(20)

式中：K表示核函數矩陣；I表示相應維數的單位矩陣.通過LSSVM進行預測的函數形式如下:

(21)

式中：k(xi,xj)表示訓練過程中的核函數，本文采用高斯(Gauss)徑向基核函數，其函數形式如下:

K(xi,xj)=exp(-‖xi-xj‖/2δ2)

(22)

式中：其中δ為核函數帶寬.在基于徑向基函數的LSSVM預測模型中，參數δ決定了訓練樣本數據分布特性，而懲罰系數γ的值能影響訓練數據的誤差以及模型的泛化能力.在進行LSSVM交通流預測時，這兩個參數的選取不當會導致預測模型過渡學習或者過擬合現象，因此有必要使用智能優化算法對δ和γ的取值進行選擇優化從而提高模型的預測性能.

6 ABOA_LSSVM短時交通流預測模型的建立

6.1 算法的基本流程

第一步搜集交通流數據，對數據做預處理，再利用ABOA對LSSVM進行參數尋優得到優化后的短時交通流預測模型，最后依據最優模型，進行短時交通預測，并輸出預測結果，具體步驟如圖5所示.

圖5 ABOA化LSSVM模型的流程框架圖

6.2 算例仿真

為了驗證提出的ABOA-LSSVM組合預測模型的有效性.選取云南省某高速5月7號-11號5天的實際交通流量數據(每10分鐘一個)，用歷史數據補齊缺失數據，然后對獲取的數據使用小波閾值降噪[18]減少異常數據對預測結果的干擾，將母小波函數ψ(x)進行變換生成一組基本小波函數:

(23)

式中a為縮放因子，b為平移因子.定義信號f(x)的連續小波變換為:

(24)

將處理后的數據采用前4天的流量作為訓練樣本集，最后一天的流量數據作為測試集進行，然后分別使用ABOA-LSSVM、WOA-、PSO-LSSVM、LSSVM這4種模型對流量數據進行預測，并與預測日的實際流量數據進行對比.文中種群大小為20，迭代次數為50代，ABOA的預測結果圖如圖6所示.

圖6 ABOA優化LSSVM短時交通流預測值與實際值對比

6.3 預測結果對比

對于3種不同算法的預測結果，為了體現其有效性，本文通過使用采用均方誤差(MSE)、平均絕對百分比誤差(MAPE)這兩個值作為評價指標，指標的表達式如下所示:

(25)

(26)

本文將不同模型計算的預測值和真實值的均方誤差、平均絕對百分比誤差結果放在表5中，由表5本文可以看出使用ABOA-LSSVM模型做短時交通流預測預測結果上整體優于其他幾種模型，說明使用的ABOA-LSSVM模型在進行短時交通流預測是可行的.

表5 模型誤差

7 結 論

本文提出了使用自適應權重和天牛須搜索的策略對鯨魚優化算法進行了改進，在進行搜索捕食將鯨魚個體看做天牛個體，使用天牛須搜索的策略避免了搜索捕食的隨機性大大加快了前期的全局搜索速度，同時使用自適應權重策略使得算法后期的搜索精度.通過對18個標準測試函數的仿真實驗可得改進后的算法在收斂精度，穩定性及收斂速度上相對于標準WOA、PSO、GA 3種算法均有著明顯的優勢，證明了改進策略的有效性.然后將改進后的算法結合LSSVM進行短時交通流預測，并與標準WOA,PSO優化LSSVM以及LSSVM短時交通流預測進行對比,結果表明改進后的算法在LSSVM短時交通流預測上的有效性.