基于FLUENT扭王字塊體護面斜坡堤越浪量的數值研究
孫大鵬,修富義,王 鍵,趙沛泓,董 勝,李玉成
(1.大連理工大學 海岸和近海工程國家重點實驗室,大連 116024;2.大連軟件園榮泰開發有限公司,大連 116024;3.中交第一航務工程勘察設計院有限公司,天津 300222;4.中國海洋大學,青島 266100)
越浪量關系著斜坡堤自身結構和堤后陸域的安全性,是斜坡堤設計中重點關注的指標之一。關于斜坡堤越浪量的估算,目前主要采用物理模型試驗和數值模擬計算兩種方法。由于數值模擬方法不受場地限制,能夠克服模型比尺影響等優點,近些年,有很多學者對斜坡堤越浪進行數值研究。Kobayashi[1]和Hu[2]均應用NLSW模型模擬光滑混凝土板護面斜坡堤的越浪過程;Losada[3]和Guanche[4]采用COBRAS-UC模型對斜坡堤越浪量和胸墻受力進行數值計算;王鍵[5]、楊錦凌[6]均應用FLUENT軟件,數值研究光滑混凝土板護面斜坡堤越浪過程,并對坡肩寬度這一影響因素進行了探討。張九山[7]通過添加多孔介質區模擬護面塊體,數值研究護面塊體在斜坡堤不同位置時對越浪的影響;王鵬[8]應用FLUENT軟件,通過添加多孔介質區,數值研究塊體護面斜坡堤爬高過程,建立了慣性阻力系數與糙滲系數的關系;王鑫玨和張慶河[9]以曼寧系數作為等效摩阻系數,研究了人工塊體護面斜坡堤越浪的變化;李東洋[10]基于OpenFOAM,通過網格劃分工具對斜坡堤外層扭王護面塊體進行全尺度精細劃分模擬,研究了正相入射不規則波與扭王字塊體護面斜坡堤的相互作用;黃寧[11]利用FLUENT軟件,基于質量源造波和動量源消波的方法,研究了平臺寬度、斜坡坡度對越浪量的影響。前人的數模研究多數是對光滑混凝土板護面斜坡堤越浪量的研究,對塊體護面斜坡堤研究較少;在應用FLUENT軟件數值模擬塊體護面斜坡堤越浪量的過程中,如何簡便準確地確定多孔介質區的慣性阻力系數取值一直是該數值方法難以突破的瓶頸。
針對現行《港口與航道水文規范》[12]中尚未給出扭王字塊體護面斜坡堤越浪量計算方法的現狀,本文應用FLUENT軟件,建立多孔介質區數值模型,綜合考慮波陡、相對水深、相對堤頂超高、相對坡肩寬度、相對胸墻高度和相對塊體尺寸等多種影響因素,數值模擬坡度m=1.5的扭王字塊體護面斜坡堤越浪過程,并結合物理模型試驗,給出了扭王字護面塊體慣性阻力系數C的計算公式。應用該公式,可以較為準確地確定慣性阻力系數,使得FLUENT軟件能夠獨立開展數值模擬,并可以較為精確地計算扭王字塊體護面斜坡堤越浪量,為斜坡堤越浪量進一步的數值研究提供了參考。
1 數值波浪水槽
1.1 水槽概況
本文基于唐蔚[13]和王鍵[5]的主動吸收式造波理論,構建如圖1所示的波浪數值水槽,其中水槽全長25 m,高0.8 m,左端為造波邊界,右端為6 m長的消波區。

圖1 數值波浪水槽(單位:m)Fig.1 Numerical wave sink
1.2 性能驗證
不規則波采用JONSWAP譜(γ=3.3),模擬的試驗波況如下:有效波高Hs為0.112 6 m,譜峰周期Tp為1.55 s,水深d為0.45 m。在水槽中x=15.0 m和19.0 m兩處采集波面數據并對其分析,模擬譜與靶譜的對比見圖2,對比模擬波浪與目標波浪的統計波浪要素見表1。

2-a x=15.0 m2-b x=19.0 m圖2 靶譜與模擬譜的對比Fig.2 Comparison between the target spectrum and simulated spectrum
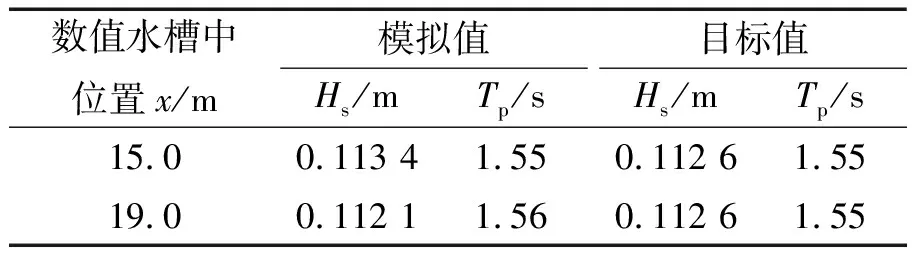
表1 有效波高、譜峰周期模擬值與目標值的對比Tab.1 Comparisons of simulated and the target values of significant wave height and peak period
由表1和圖2可以看出,模擬波浪與目標波浪的統計波要素及頻譜均吻合良好,表明該數值波浪水槽能夠有效地模擬不規則波。
2 多孔介質區中慣性阻力系數C的率定
2.1 數模工況組合
采用上一節介紹的數值波浪水槽,運用FLUENT軟件,建立多孔介質區模型,模擬計算扭王字塊體護面斜坡堤(m=1.5)越浪量,多孔介質模型的方程和邊界條件參照王鵬[8],在考慮波浪不破碎的情況下,數值模擬工況組合參照孫大鵬[14]物理模型試驗確定,如表2所示,試驗斷面如圖3所示。不同重量的扭王字塊體以尺寸h區分,h如圖4所示,試驗中采用的滿足穩定性要求的扭王字塊體尺寸h為4.2 cm、6.0 cm和7.8 cm。
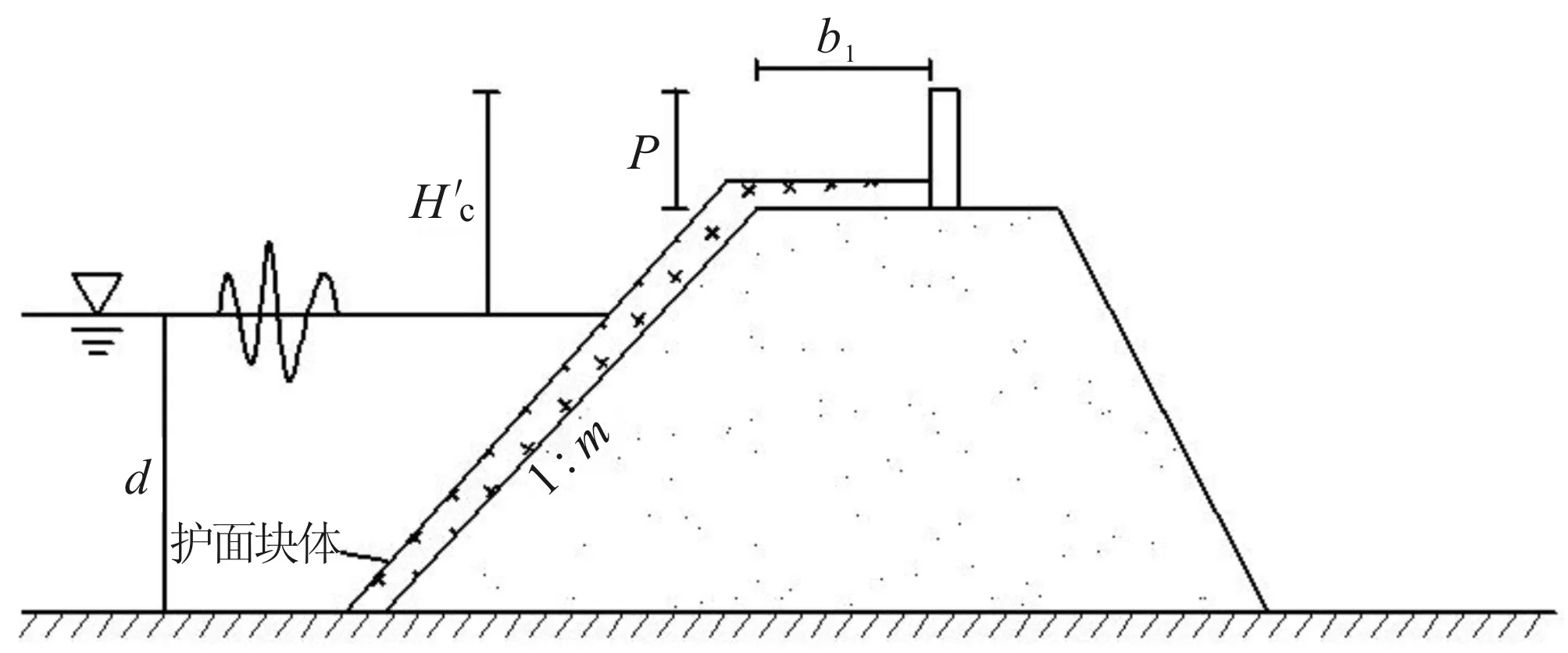
圖3 試驗斷面圖Fig.3 Shape of test section

圖4 扭王字塊體尺寸圖Fig.4 Shape of the accropode blocks
2.2 慣性阻力系數與越浪量的關系
采用表2中的15種工況組合(參照孫大鵬[14]),h為4.2 cm、6.0 cm和7.8 cm三種扭王字塊體,共計數值模擬45組。針對每種工況和不同的扭王字塊體尺寸h,建立對應的多孔介質區模型,確定C值的方法如下:
在FLUENT軟件中,運用上述建立的數值模型,設定不同的C值,計算出不同C值下的越浪量。以C為橫軸,對應C值下的斜坡堤越浪量為縱軸,采用指數函數擬合,得出C與相應越浪量的關系圖,本文慣性阻力系數C取值為0.1、0.5、1、2和5。當h=4.2 cm時,表2中不同工況慣性阻力系數C與越浪量的關系如圖5中(1)~(15)所示,采用孫大鵬[14]一文中的物模試驗值,按圖5中虛線所示,查找不同工況下越浪量對應的慣性阻力系數C,得到C值如表3所示。

表2 試驗工況組合Tab.2 Combination of the experimental conditions
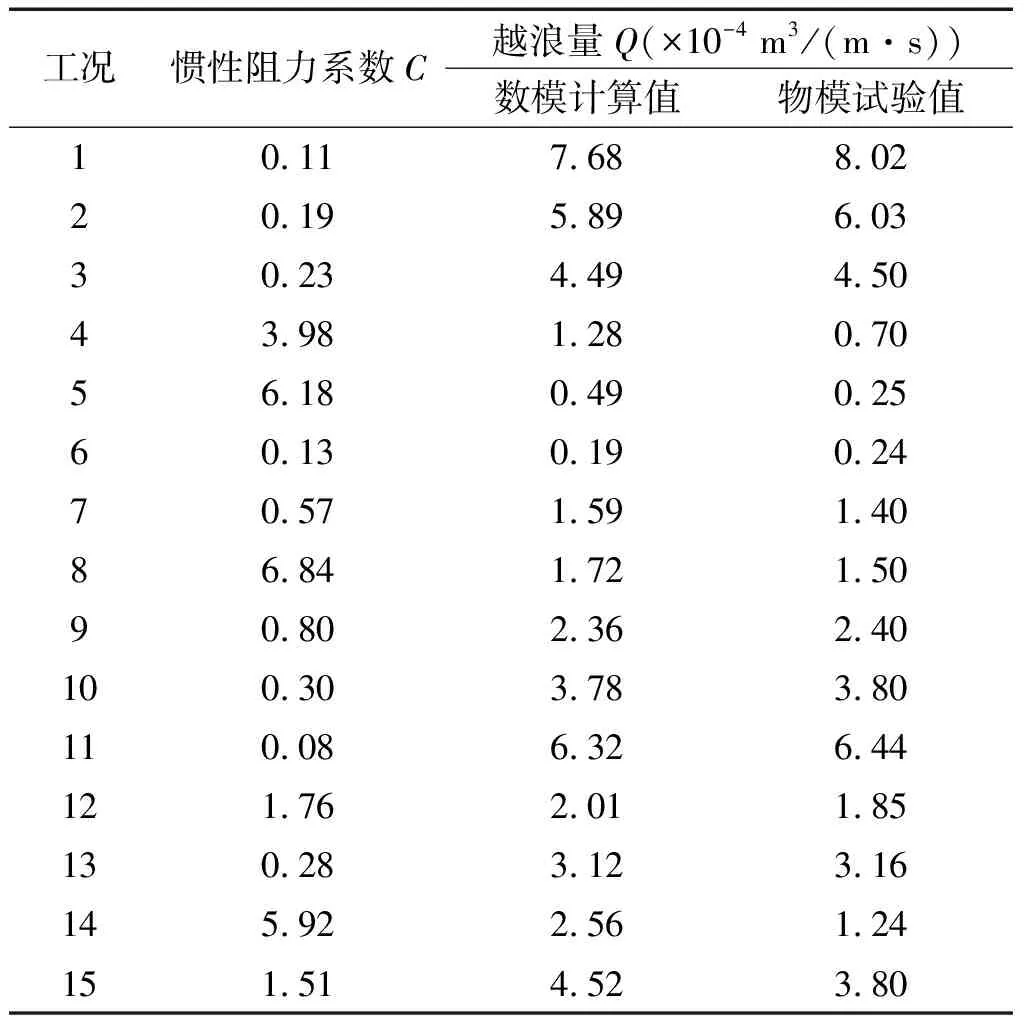
表3 慣性阻力系數C和數值計算越浪量值(h=4.2 cm)Tab.3 The inertia resistance coefficient and mean overtopping numerical results(h=4.2 cm)

5-a 工況15-b 工況25-c 工況3
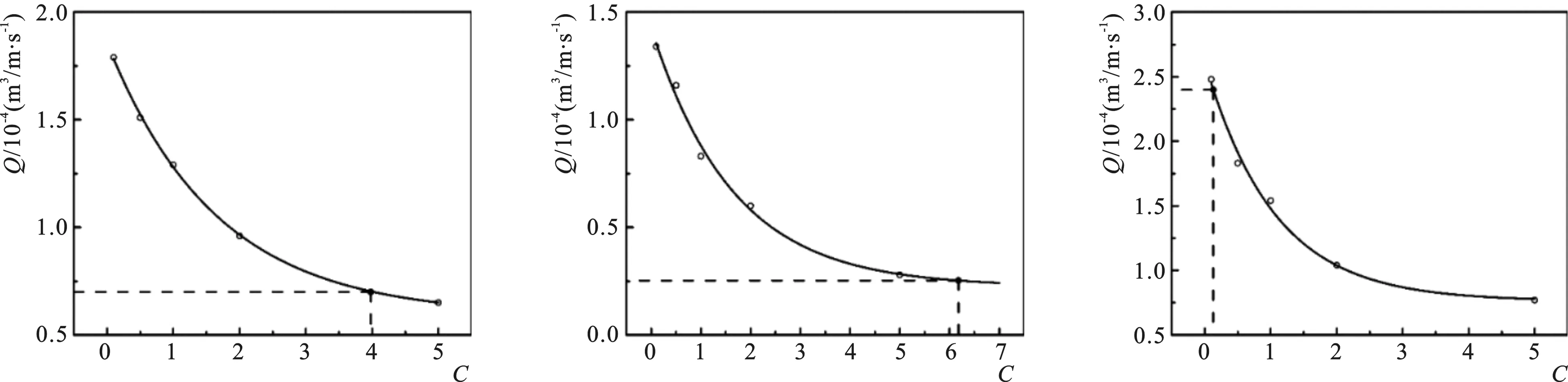
5-d 工況45-e 工況55-f 工況6

5-g 工況75-h 工況85-i 工況9
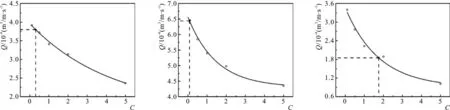
5-j 工況105-k 工況115-l 工況12
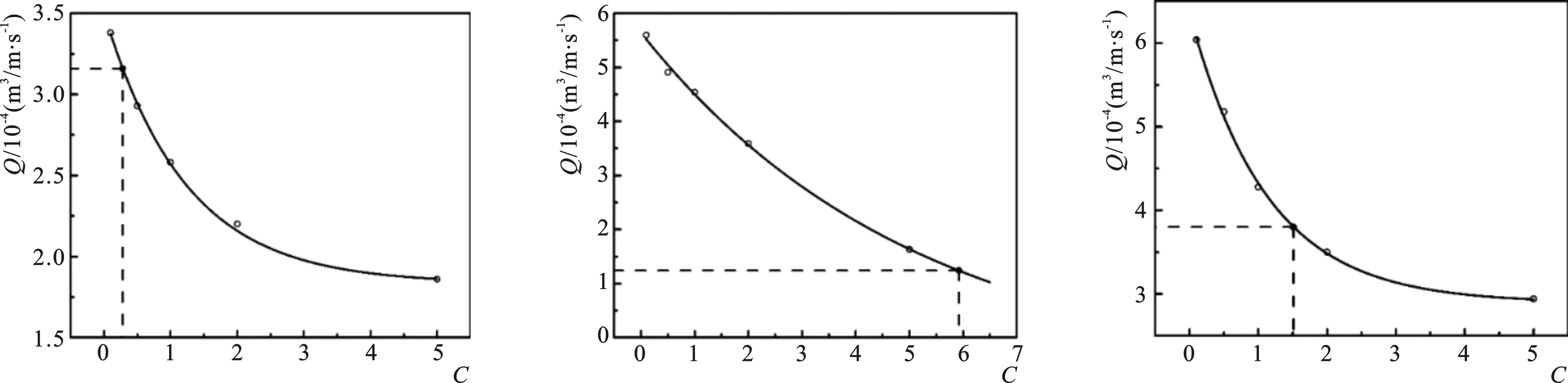
5-m 工況135-n 工況145-o 工況15圖5 越浪量Q與慣性阻力系數C的關系曲線(h=4.2 cm)Fig.5 Relational graph of Q versus C (h=4.2 cm)
采用同樣方法,分別確定出h=6.0 cm和h=7.8 cm時,每種工況下扭王字護面塊體的慣性阻力系數C如表4、5所示。
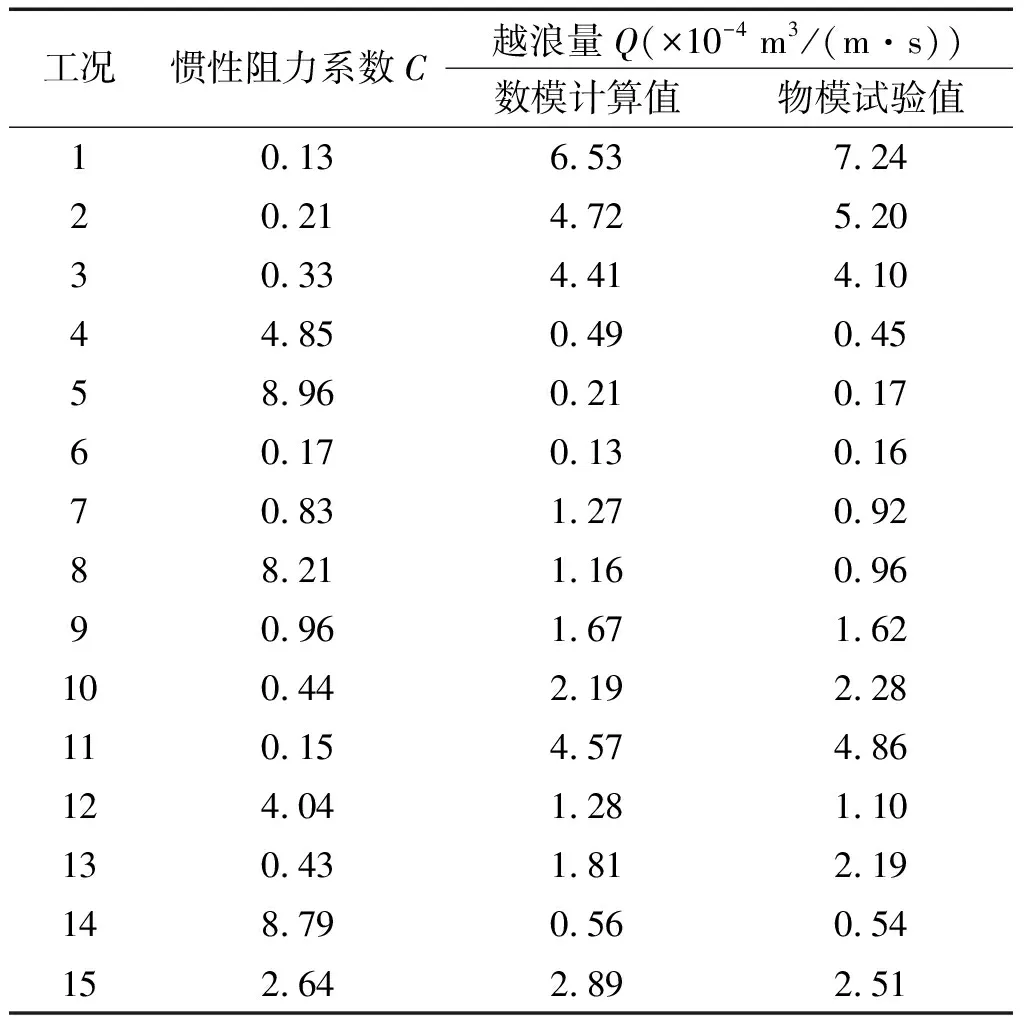
表4 慣性阻力系數C和數值計算越浪量值(h=6.0 cm)Tab.4 The inertia resistance coefficient and mean overtopping numerical results(h=6.0 cm)
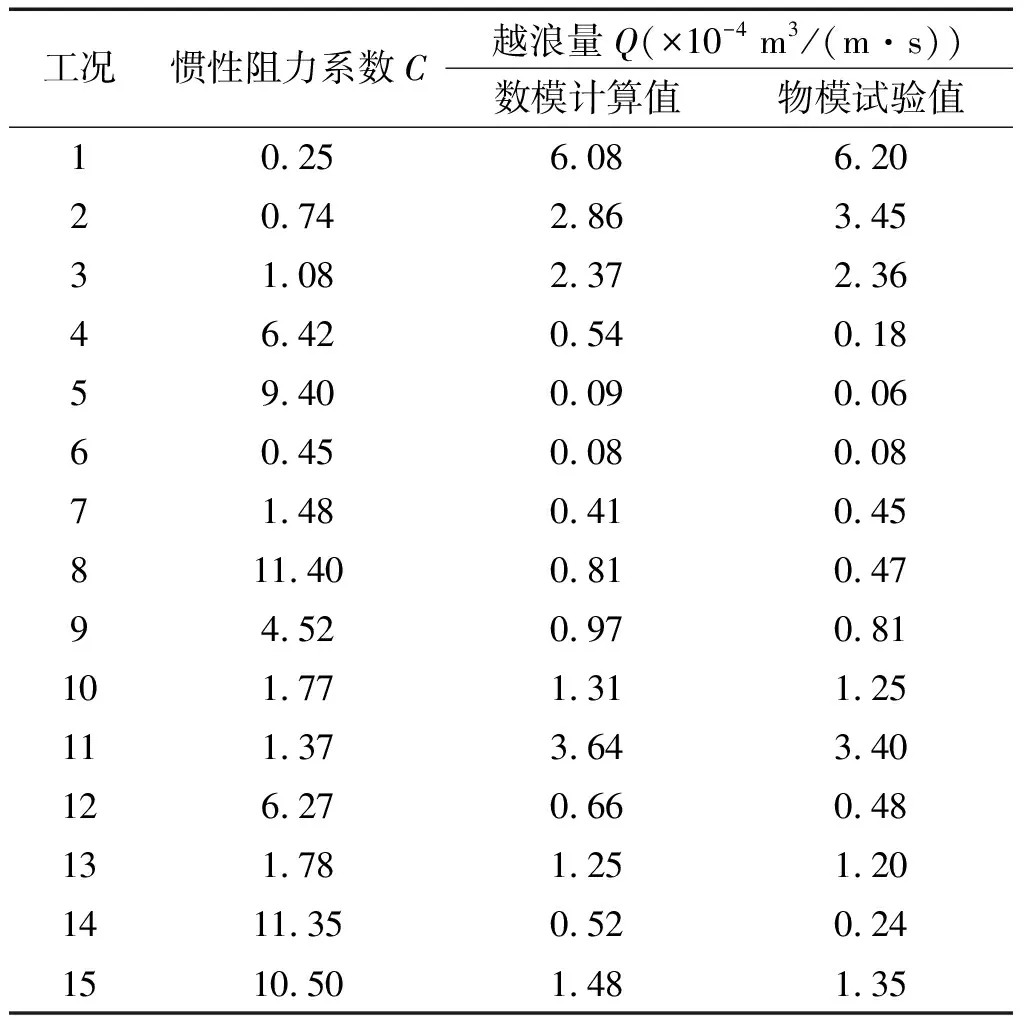
表5 慣性阻力系數C和數值計算越浪量值(h=7.8 cm)Tab.5 The inertia resistance coefficient and mean overtopping numerical results(h=7.8 cm)
參照孫大鵬[14]物模試驗值,運用查慣性阻力系數C與越浪量關系圖的方法,得到表3~5中不同工況的C值。為確定該方法得到C值的合理性,將不同工況下得到的C值代入相應的扭王字塊體護面斜坡堤數值模型中計算越浪量,結果見表3~5,以物模試驗值為橫軸,數模計算值為縱軸,得到兩者對比圖如圖6所示。
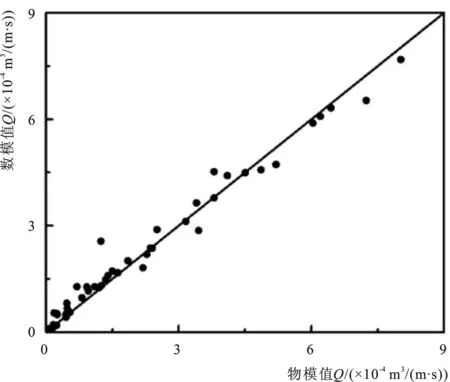
圖6 Q物模試驗值與數模計算值的對比圖Fig.6 Comparison of Q between predicted and measured values
從圖6可以看出,物模試驗值與對應的數模計算值在直線y=x兩側均勻分布,二者吻合較好。說明只要能夠合理地確定C,應用FLUENT軟件中的多孔介質模型,就可以較為準確地計算出扭王字塊體護面斜坡堤的越浪量。
3 扭王字護面塊體慣性阻力系數C的計算關系式
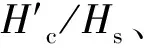
(1)
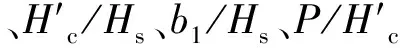
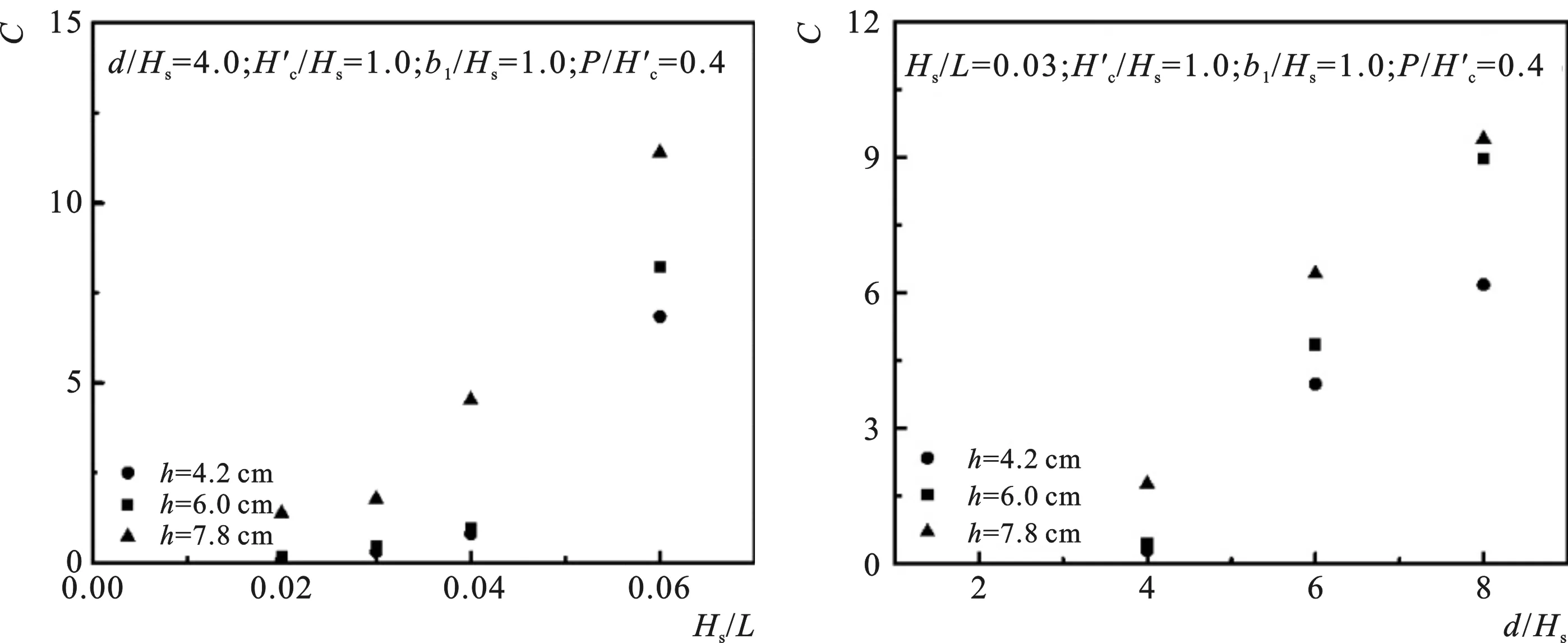
圖7 C與Hs/L的關系 圖8 C與d/Hs的關系 Fig.7 Relational graph of C versus Hs/LFig.8 Relational graph of C versus d/Hs
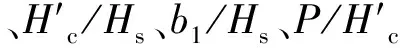
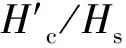
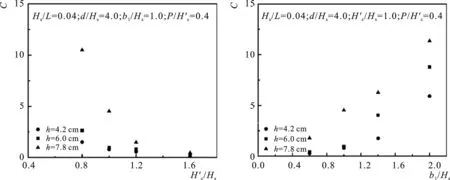
圖9 C與的關系 圖10 C與b1/Hs的關系 Fig.9 Relational graph of C versus Fig.10 Relational graph of C versus b1/Hs
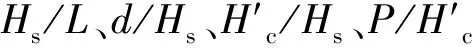
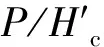
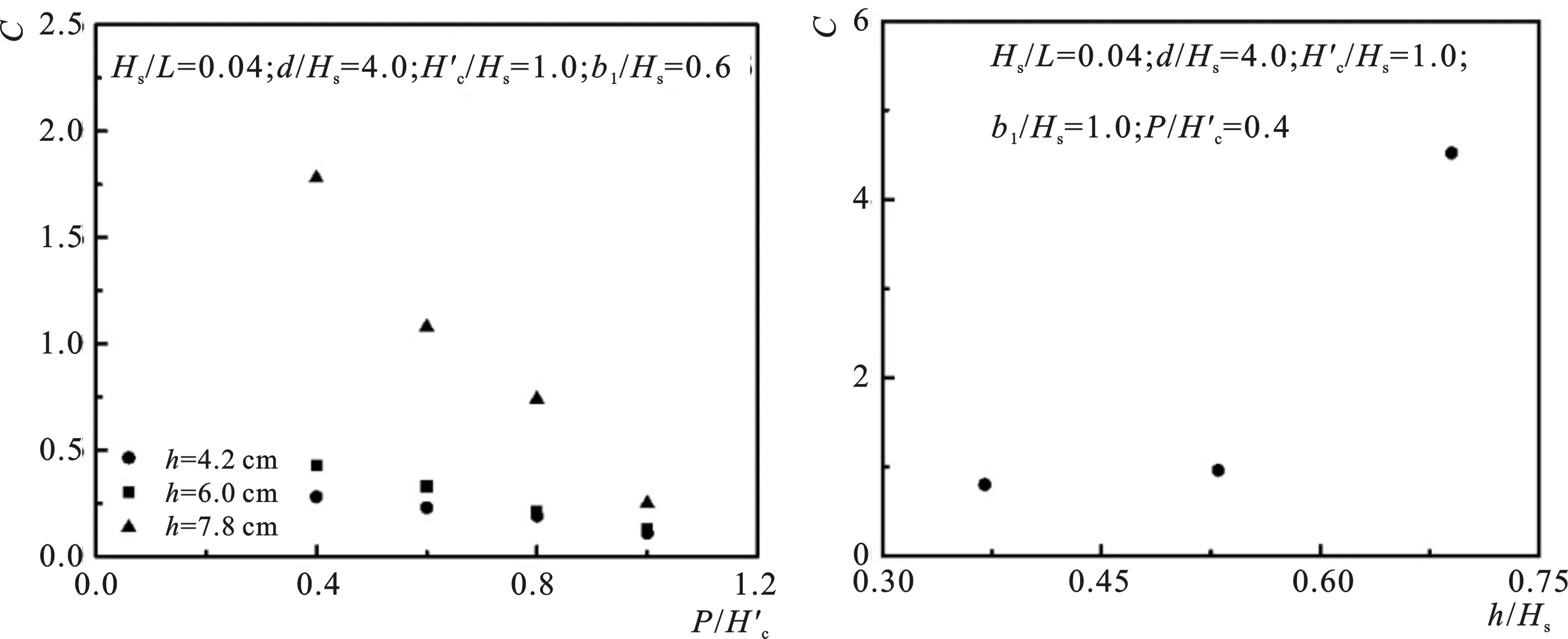
圖11 C與的關系 圖12 C與h/Hs的關系 Fig.11 Relational graph of C versus Fig.12 Relational graph of C versus h/Hs

(7)C的計算關系式。根據以上分析,本文綜合考慮各影響因素,并采用非線性擬合運算,在坡度m=1.5的特定情況下,得到C的計算關系式
(2)
上式相關系數R>0.90,滿足擬合方程的相關性要求。表6為不同扭王字塊體尺寸在表2中的工況組合下,運用計算式(2)得出相應扭王字護面塊體慣性阻力系數C。為確定計算式(2)得到C值的精確性,將表6中的C值帶入相應數值模型中計算出越浪量,并與物模試驗值(孫大鵬[12])比較,對比結果如圖13所示。

表6 公式(2)C的計算值Tab.6 Formula calculated value of C
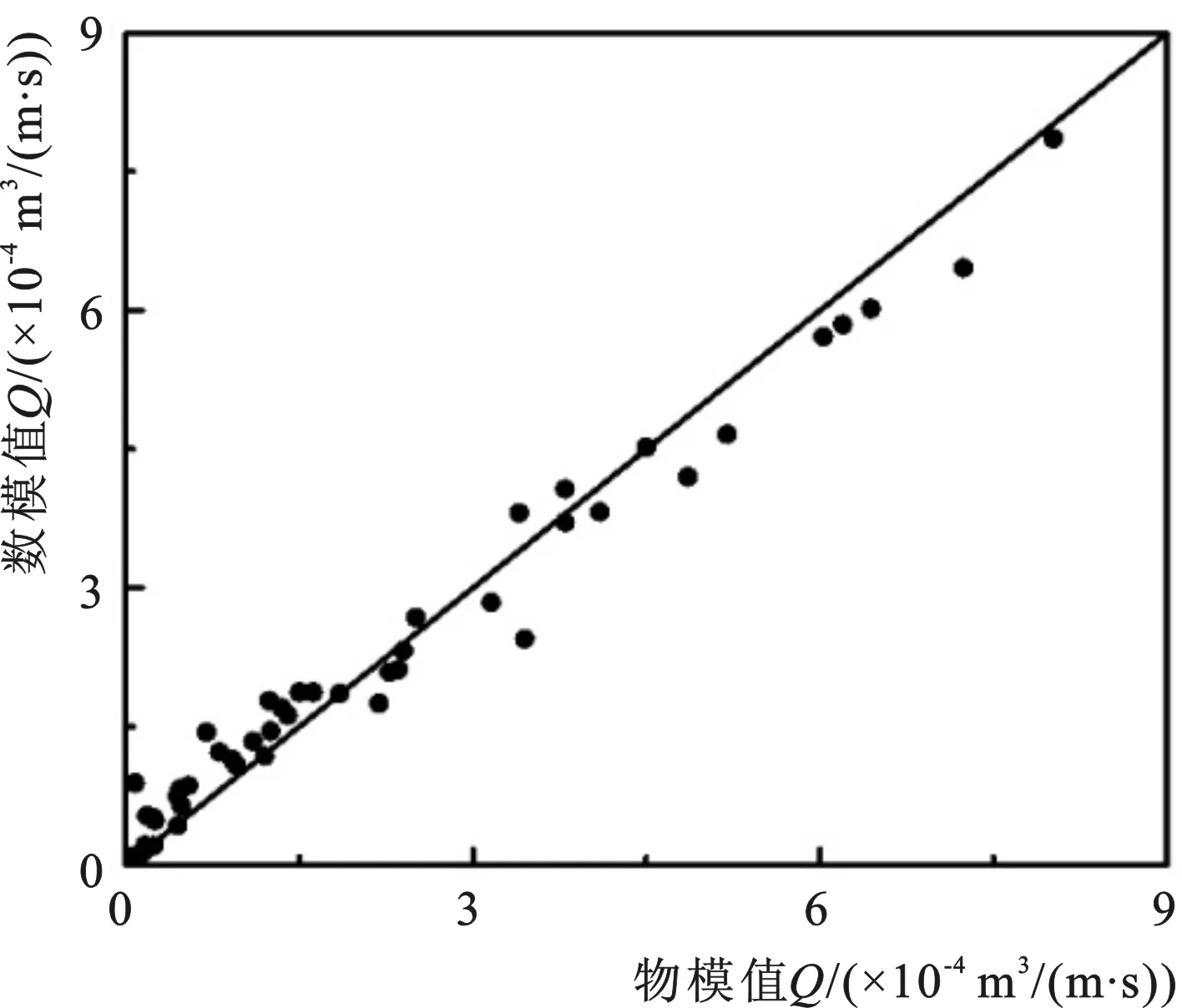
圖13 Q物模值與數模值對比Fig.13 Comparison of Q between predicted and measured value
由圖13所示,越浪量物模試驗值和數模計算值在直線y=x兩側均勻分布,二者吻合較好,表明本文計算式(2)得到的C值具有較好的精確性,在各影響因素處以計算式(2)的適用范圍內時,可以直接運用該計算式得到C值,進而數值模擬計算出扭王字塊體護面斜坡堤的越浪量。
4 結論
(1)借助FLUENT軟件,建立多孔介質區模型,數值模擬得到C與越浪量關系曲線,對應查找物模試驗值,確定不同工況下的C值。在此基礎上,綜合多種影響因素分析,首次得到扭王字護面塊體慣性阻力系數C的計算關系式,該計算式考慮因素較多,具有合理性和一定的工程實用性;(2)將計算式(2)得到的C值帶回數值模型中計算出相應越浪量,與物模試驗值吻合良好,表明本文構建的數值方法具有較好的精確性與合理性。該數值方法為扭王字塊體護面斜坡堤越浪量的深入研究開辟了一條新途徑,使得FLUENT軟件無需借助物模實驗,能夠獨立計算扭王字塊體護面斜坡堤越浪量,并對其他種類塊體護面斜坡堤的數值研究具有借鑒意義。

