借助直觀圖形解決重疊問題
邱廷建
小朋友,我們知道解答求和問題時,只要直接把各部分數加起來,就可以得到答案。但是,計算部分有重復的時候,問題就不那么簡單了,我們把這類問題稱為重疊問題。在解答重疊問題時,我們可以借助直觀圖形,化抽象為直觀,運用“包含與排除”原理,理清數量關系:當兩個部分有重復包含時,應去掉重復部分,不重復計數,也就是要從它們的和中減去重復的數。
現在,我們一起來學習解決人教版教材三年級上冊第九單元的有關重疊問題。
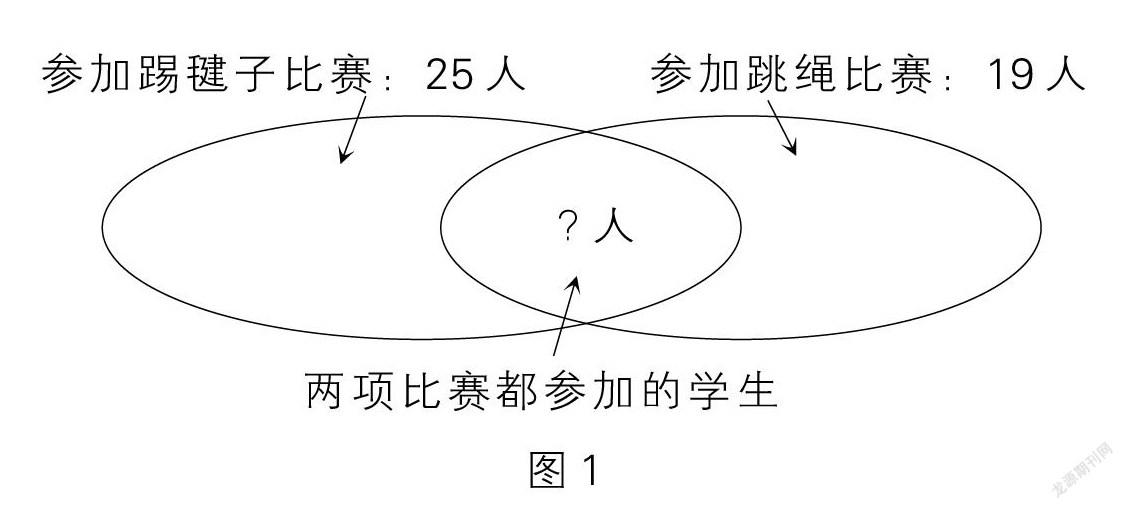
例1 新亭小學三(1)班共有學生38人,每人至少參加踢毽子和跳繩兩項比賽中的其中一項。已知參加踢毽子的有25人,參加跳繩的有19人。求兩項比賽都參加的學生有多少人?
[分析與解]根據題意,我們可以畫出如圖1所示的直觀圖。
從圖1中我們可以看出,求兩項比賽都參加的學生有多少人,就是求中間的重疊部分。把參加踢毽子比賽的25人加上參加跳繩比賽的19人,和是25+19=44(人),44人比全班總人數38人多,是因為重疊部分多算了一次,所以重疊部分,也就是兩個項目比賽都參加的學生人數是44-38=6(人)。綜合算式是25+19-38=6(人)。
從圖1中我們還可以看出,用全班總人數38人減去參加踢毽子比賽的人數是38-25=13(人),這13人是只參加跳繩比賽而沒有參加踢毽子比賽的學生人數。而參加跳繩比賽的有19人,說明這19人中有一部分既參加了跳繩比賽也參加了踢毽子比賽,從參加跳繩比賽的人數中減去只參加跳繩比賽的人數,剩下的就是兩個項目比賽都參加的人數,算式是19-13=6(人)。綜合算式是19-(38-25)=6(人)。同樣的道理,我們還可以這樣列綜合算式解答25-(38-19)=6(人)。
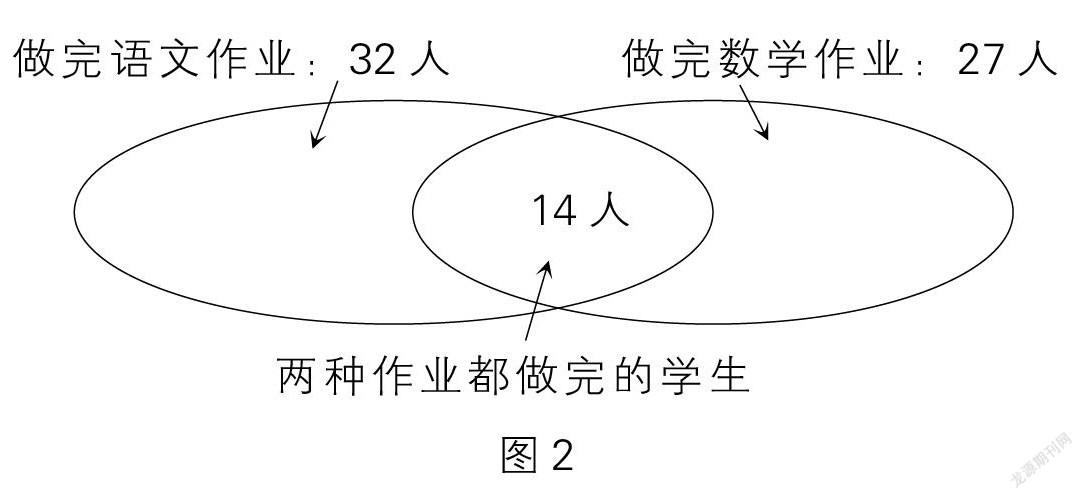
例2 紅星小學三(2)班做完語文作業的有32人,做完數學作業的有27人,兩種作業都完成的有14人,每人至少完成一種作業。三(2)班共有學生多少人?
[分析與解]根據題意,我們可以畫出如圖2所示的直觀圖。
從圖2中我們可以看出,中間的重疊部分表示兩種作業都完成的有14人。這14人既包含在做完語文作業的32人中,又包含在做完數學作業的27人中,而做完兩種作業的一共有32+27=59(人),這59人中就重復計算了14人。因此要從做完兩種作業的總人數中減去重復計算的14人,就是三(2)班的學生人數,算式是59-14=45(人)。綜合算式是32+27-14=45(人)。
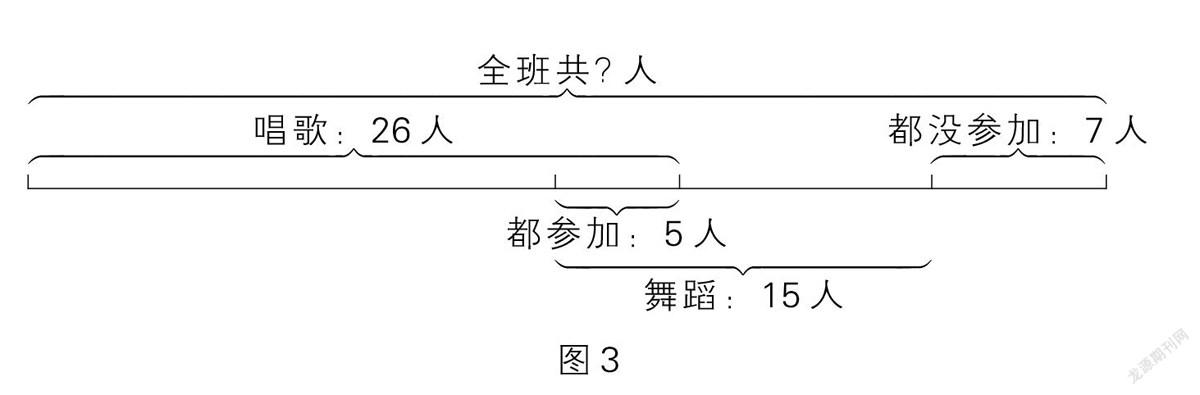
例3 育才小學三(3)班舉辦“元旦”聯歡會,參加唱歌表演的有26人,參加舞蹈表演的有15人。兩項都參加的有5人,兩項都沒有參加的有7人。三(3)班共有學生多少人?
[分析與解]根據題意,我們可以畫出如圖3所示的直觀圖。
從圖3中我們可以看出,中間的重疊部分表示兩項表演都參加的有5人。用參加舞蹈表演的人數減去重疊部分的人數就是只參加舞蹈表演的人數,算式是15-5=10(人)。用參加唱歌表演的人數加上只參加舞蹈表演的人數,再加上兩項都沒有參加的人數,就是全班的總人數,算式是26+10+7=43(人)。綜合算式是26+(15-5)+7=43(人)。
結合圖3,我們也可以這樣思考,用參加唱歌表演的人數減去重疊部分的人數就是只參加唱歌表演的人數,算式是26-5=21(人)。用只參加唱歌表演的人數加上參加舞蹈表演的人數,再加上兩項都沒有參加的人數,就是全班的總人數,算式是21+15+7=43(人)。綜合算式是26-5+15+7=43(人)。
例4 高新小學三(4)班有學生40人,做對第一道思考題的有24人,兩道思考題都做對的有9人,兩道思考題都做錯的有8人。做對第二道思考題的有多少人?
[分析與解]根據題意,我們可以畫出如圖4所示的直觀圖。
從圖4中我們可以看出,中間的重疊部分表示兩道思考題都做對的有9人。全班有40人,兩道思考題都做錯的有8人,可以求出做對第一道思考題和第二道思考題的一共有40-8=32(人)。做對第一道思考題的有24人,兩道思考題都做對的有9人,可以求出只做對第一道思考題的有24-9=15(人)。用做對第一道思考題和第二道思考題的總人數減去只做對第一道思考題的人數,就是做對第二道思考題的人數,算式是32-15=17(人)。綜合算式是40-8-(24-9)=17(人)。
結合圖4,我們還可以這樣思考,全班有40人,兩道思考題都做錯的有8人,可以求出做對第一道思考題和第二道思考題的一共有40-8=32(人)。根據做對第一道思考題的有24人,先求出只做對第二道思考題的人數,算式是32-24=8(人)。根據兩道思考題都做對的有9人,再求出做對第二道思考題的人數是8+9=17(人)。綜合算式是40-8-24+9=17(人)。
(本文作者為福建省上杭縣教師進修學校特級教師)
小靈通上學
小靈通的新家離學校有點遠,他上學時坐車,回家時步行,在路上一共花了90分鐘;往返都坐車,只需要40分鐘;如果小靈通往返都步行,需要多少分鐘?
(參考答案見第40頁)
- 數學小靈通·3-4年級的其它文章
- 填數
- 廣告的真實性
- 和時間做朋友
- 邀你來答題
- 跟小靈通學數學知識的英語表達
- “認識更大的數”中出的錯

