軌道交通車輛全膠條密封車窗結構膠條接觸應力計算
徐 濤 朱紅茜 胡小玲 王金輝
(1.中國中車青島四方機車車輛股份有限公司,山東 青島 266111;2.湘潭大學土木工程與力學學院,湖南 湘潭 411105;3.株洲時代新材料科技股份有限公司,湖南 株洲 412007)
隨著軌道交通行業的發展,列車速度不斷地提高,車窗承受的空氣壓力和摩擦力也不斷地增大[1],對車窗安裝方式提出了更高的要求。目前,列車的車窗安裝方式主要有全膠條安裝固定連接、機械嚙合固定連接、機械嚙合和黏合劑黏接相結合連接、黏合劑黏接等。其中,黏接劑黏接在高速動車中應用最為廣泛[2],黏結劑黏接車窗能夠有效保證列車行車的安全性、舒適性和氣密性[3-5]。但是車窗更換時間長,無法快速更換。全膠條安裝固定連接(即全膠條密封車窗結構)是最為簡潔的一種,該結構無密封膠密封,維修便捷,只需要幾十分鐘就可以快速完成車窗的更換[6]。然而,全膠條密封車窗存在漏雨問題。該文以全膠條密封車窗結構為研究對象,對全膠條密封車窗漏雨情況進行力學分析;通過理論計算了密封膠條接觸應力與接觸長度設計值應滿足的關系,確保車窗不漏雨最后,將該文提出的方法應用到具體案例中,并利用ANSYS有限元軟件開展了數值模擬,對理論分析結果的可行性進行了驗證。
1 全膠條密封車窗不漏雨條件分析
軌道交通列車的全膠條密封車窗結構的連接示意圖如圖1(a)所示,車窗僅通過膠條安裝到車體上,膠條與車體和車窗的接觸面上有足夠的密封力是保證車窗不漏雨的關鍵。假設車窗安裝完好,車窗在行駛過程會受到外部風、雨載荷的作用,由于車窗尺度相對于外部壓力變化的特征尺度很小,因此可將這些載荷設定為均布載荷q0。要保證車窗在q0的作用下不漏雨,首先進行定性分析。任取一剖面,對其進行受力分析,如圖1(b)所示。膠條與車窗和車體分別都有內外2個接觸面。當車窗外側受載荷q0作用時,膠條變形,并發生微小的偏轉,車窗整體往車內側偏移,偏移嚴重時,可能使車體外側與膠條接觸面脫開,導致車窗漏雨。
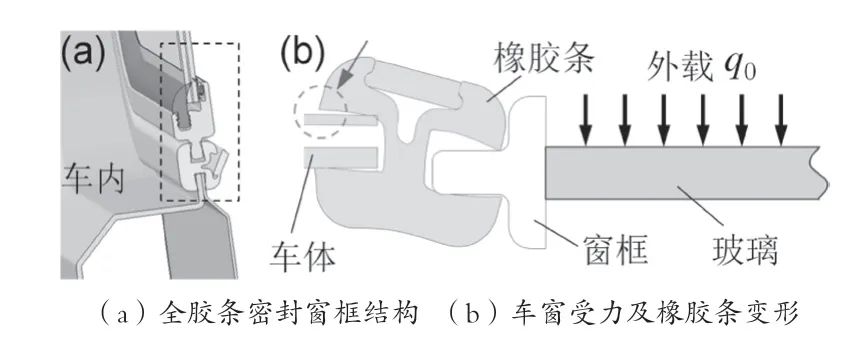
圖1 全膠條密封車窗及受力示意圖
設膠條對車體外側的密封力為F外,內側密封力為F內,如圖2所示。無均布外載時,F外=F內。有均布外載荷q0作用時,q0會在膠條與車窗和車體的4個接觸面上產生附加力F(q0) 。由于車體外側最有可能漏雨,下面僅關注膠條與車體的密封力。由受力平衡知,膠條對車體內、外側的密封力發生了變化,力的平衡方程如下。

由圖1的分析結果可知,無論在車窗外側有多大的外載作用,只要車體外側不脫開,即只要膠條對車體外側的密封力F外始終大于0,就能保證車窗不漏水。由方程(1)可知滿足車窗不漏雨的條件如下。

要保證公式(2)恒成立,則:

通過定性分析,由(3)式可知,為確保車窗不漏雨,設計膠條尺寸時,需要使膠條對車體的密封力設計值(內、外側的力相等)始終大于外載在該處產生的附加力的最大值即可。
2 外部載荷作用引起的膠條與車體接觸面上的附加力計算
在外部載荷作用下,由于膠條的偏轉,車窗相對于車體產生微小的轉動,如圖2。因此,膠條對于車窗的約束可以看作是固定鉸鏈支座。當q0作用于車窗玻璃上,在膠條約束處會產生附加的作用力F(q0),從而引起膠條對車體和車窗密封力的變化,甚至導致膠條與車體脫開。根據不漏雨條件分析結果,只要外部載荷q0在膠條與車體外側引起的附加力F(q0)始終滿足公式(3),就能保證車窗不漏雨。為求解F(q0),可將膠條約束的車窗結構簡化為四邊簡支的薄板結構進行分析,如圖3所示(垂直于玻璃窗方向觀測)。在外界均布載荷q0的作用下,四邊簡支支座反力即為作用力F(q0)。

圖2 車窗膠條與車體接觸面上的密封力及外載示意圖
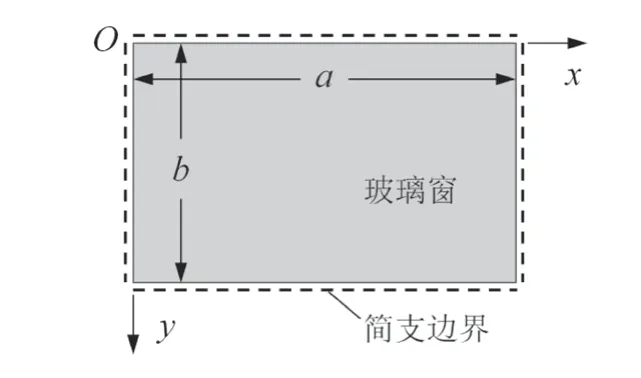
圖3 全膠條密封車窗簡化的四邊簡支薄板結構
如圖3所示,玻璃窗的2個邊長分別為a和b,厚度為t。在玻璃窗平面內建立平面直角坐標系Oxy。假設外界均布載荷q0的作用下在垂直于xy平面產生的撓度為w(x,y),利用簡支矩形薄板的納維葉(Navier)解法,撓度w(x,y)的表達式可以用下面的重三角級數表示[7]:
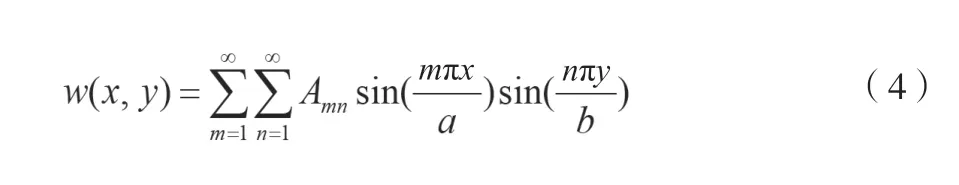
其中,m,n=1,3,5,7,…,取奇數。在均布載荷q0作用下,系數Amn如下。
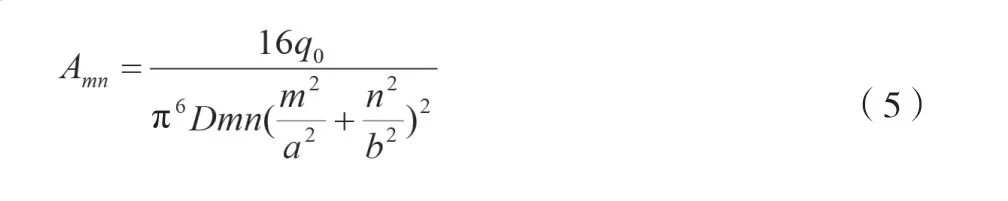
如圖4所示,四邊簡支薄板中x橫截面和y橫截面上單位長度的剪切內力如下。

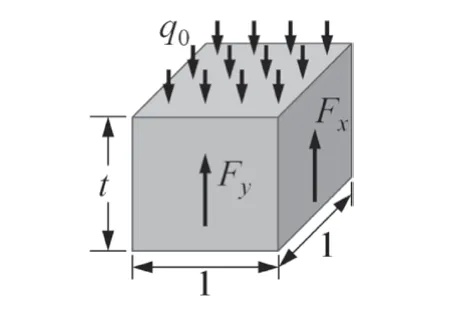
圖4 厚度為t,長、寬均為單位長度1的微元六面體中剪切內力示意圖

假設膠條在x=0、a2個邊界上對車體的接觸應力和接觸長度分別為qa和δa,膠條在y=0、b2個邊界上對車體的接觸應力和接觸長度分別為qb和δb,則不漏雨的條件如公式(8)所示。

一般情況下,在全膠條密封車窗結構的實際設計中,會使qa=qb,δa=δb。假設qa=qb=q,δa=δb=δ,則根據公式(8):
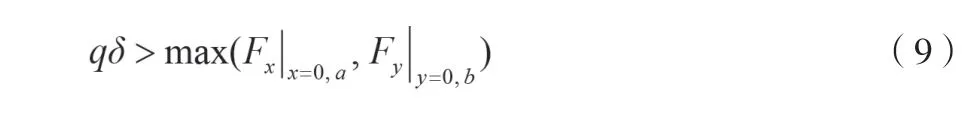
式(9)表明:膠條與車體的接觸應力q和接觸長度δ設計值的乘積要大于外載作用引起的膠條與車體接觸面上單位長度附加力的最大值才能保證車窗不漏雨。
3 全膠條密封車窗膠條接觸應力計算實例
為驗證車窗受外部載荷作用下力學分析的正確性,該文采用有限元計算軟件ANSYS對某軌道車輛車窗玻璃在外界均布載荷作用下的變形問題進行了數值模擬。車窗玻璃多采用多層中空結構,該文主要研究外載作用引起的膠條與車體密封力的變化,忽略中空結構,將車窗玻璃看成厚度t為6.2mm,長a、寬b均為990mm的單層鋼化玻璃(該尺寸來源于中車四方芝加哥某項目的軌道車輛車窗尺寸)。由此,該文通過四邊簡支的矩形薄板來模擬車窗結構,得到鉸支座處的約束反力數值結果,即外界載荷作用下,在膠條與車體接觸面上產生的附加力,并與理論分析結果進行對比。材料參數包括[8-9]鋼化玻璃密度ρ=2530kg/m3,彈性模量E=70GPa,泊松比μ=0.21。車體與膠條表面間的靜摩擦系數γ為0.672。在模型周邊施加簡支約束,載荷條件為均布面載荷q0,以芝加哥一年中最大的風載荷945Pa作為載荷條件,即q0=945Pa。車窗玻璃有限元計算模型如圖5所示,模型采用殼體單元,單元數為841,節點數為900。圖6顯示了數值模擬的變形云圖結果。從圖中可以看出,在外界均布載荷作用下玻璃窗的中心點處變形最大,四邊簡支的邊界上沒有變形,這與理論分析中邊界上的撓度為0的結果相符合。

圖5 車窗玻璃的有限元計算模型
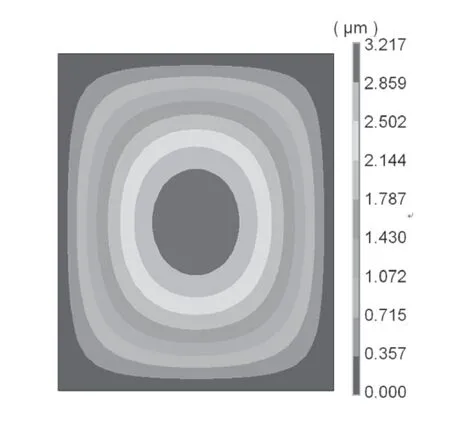
圖6 車窗玻璃在外界均布載荷作用下的變形云圖
由于車窗長a和寬b相等,由對稱性可只研究一個邊界上的作用力。該文考察隨坐標y變化的結果。將車窗材料性能參數及尺寸參數代入式(6),便可求得外載引起的附加力隨坐標y的變化。圖7給出了理論分析與數值模擬的對比結果,兩者符合很好,與已有研究結果變化規律相同[10],說明了理論分析結果的正確性。外部載荷q0作用在車窗上,在膠條與車體接觸面上產生了附加力,從理論和仿真結果可以看出,該作用力大小沿邊長呈拋物線形狀變化,在車窗四邊中心點處有最大值。理論分析得到單位長度的作用力最大值為306.19N/m, ANSYS模擬得到的該作用力的最大值為315.69N/m,兩者誤差為3.1%。由(11)式可知,膠條與車體的接觸應力和接觸長度設計值q和δ的乘積應滿足,qδ>309.19 N/m。根據計算結果,在圖8中給出了q和δ的乘積結果曲線和車窗在外載下不漏雨的設計區域。
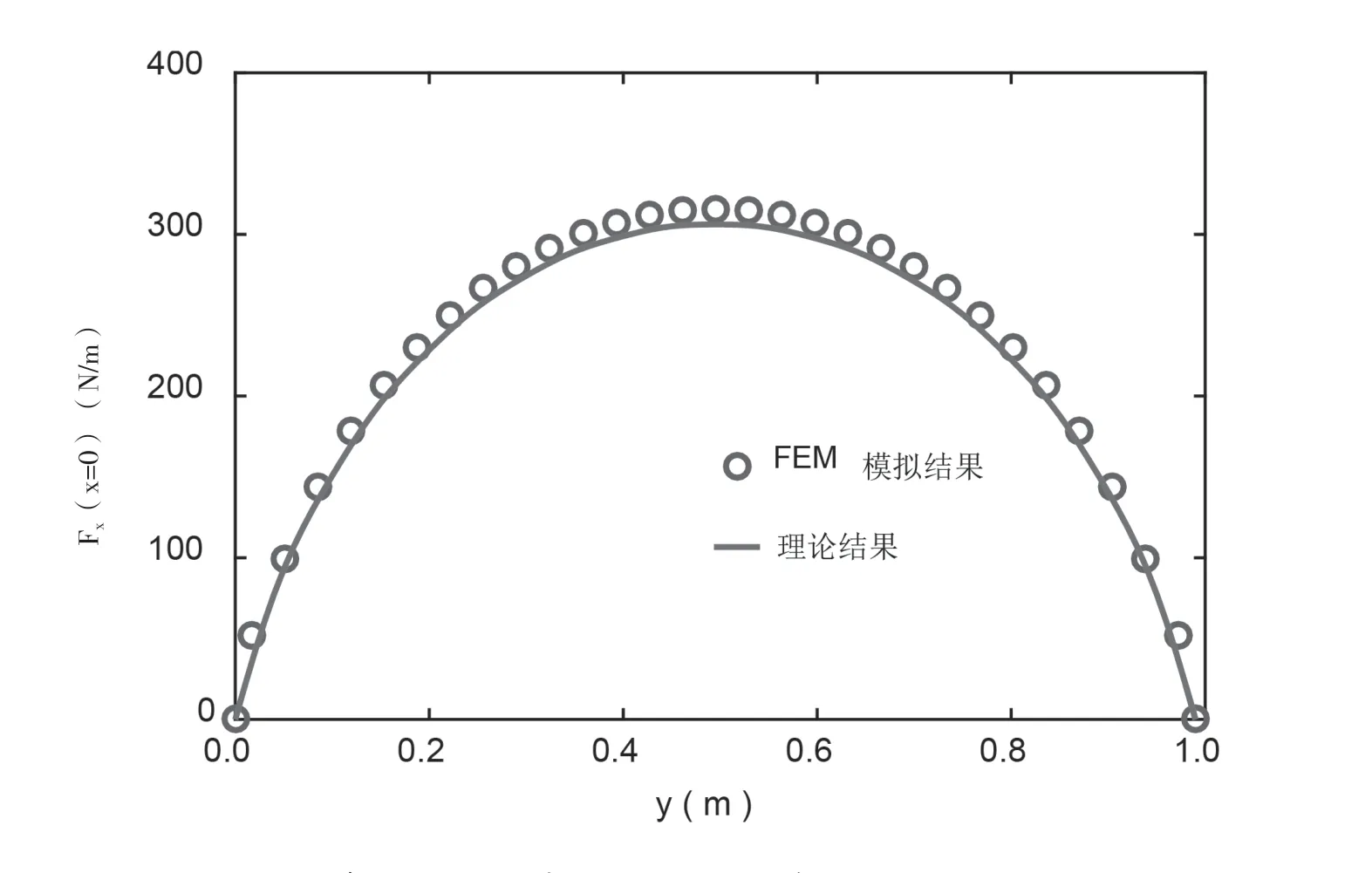
圖7 單位長度附加力隨窗框邊長變化的理論分析和數值模擬結果對比
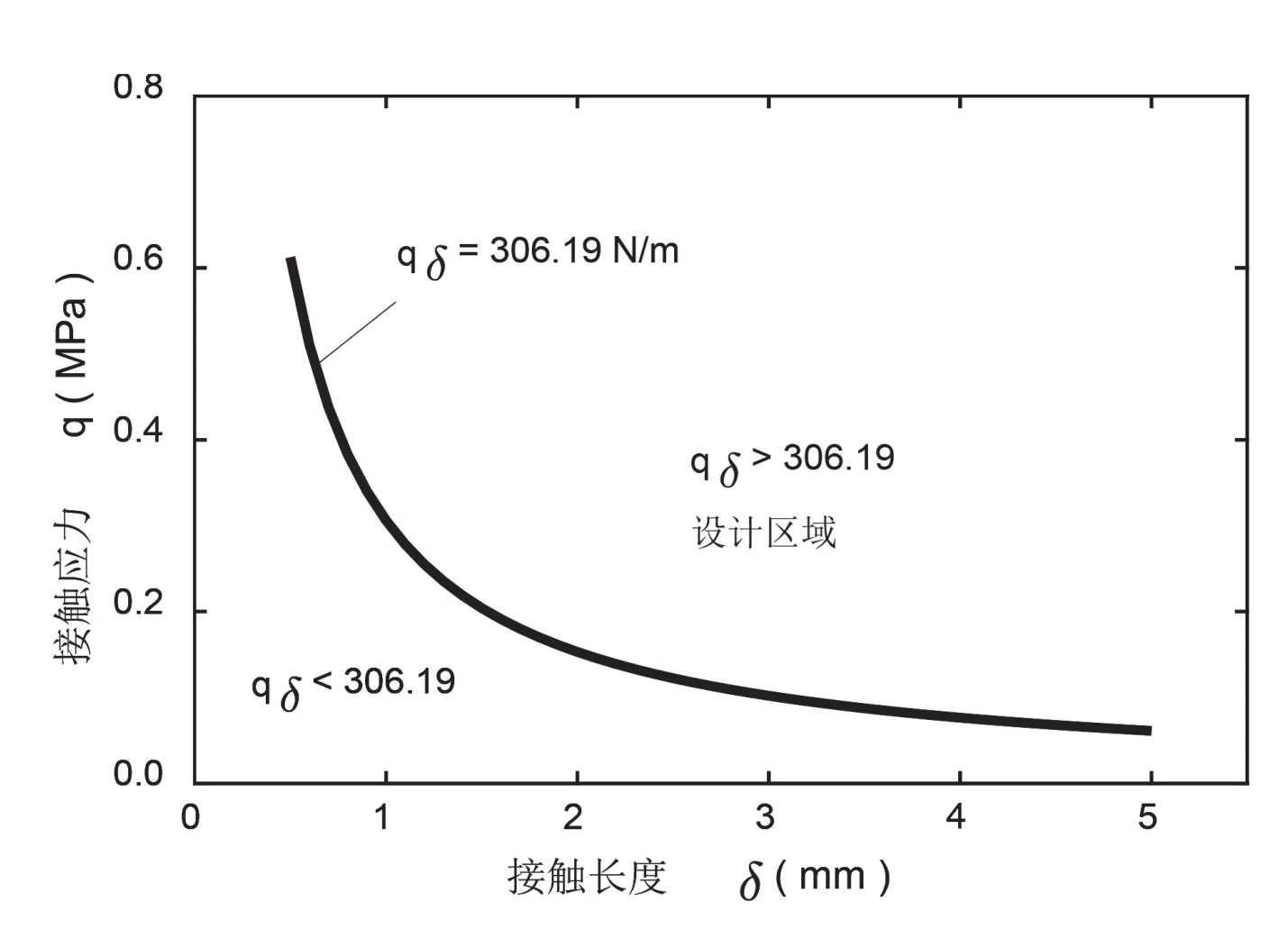
圖8 膠條與車體接觸面上的接觸應力q和接觸長度δ乘積結果
4 結語
該文以全膠條密封車窗結構為研究對象,首先對全膠條密封車窗漏雨情況進行了定性分析,只要膠條對車體的密封力設計初值始終大于外載引起的膠條與車體外側接觸面上的附加力最大值,車窗就不會漏雨。通過板殼力學理論分析了車窗玻璃受均布載荷的問題,得到了不漏雨條件下膠條與車體的接觸應力與接觸長度設計值應滿足的關系式。將該文提出的方法應用到具體案例中,發現外部載荷作用于車窗玻璃引起的膠條與車體接觸面上的附加力大小沿邊長呈拋物線形狀變化,車窗四邊中心點處的作用力最大。利用ANSYS軟件對車窗受外部載荷作用情況開展了有限元數值模擬,對比驗證了理論分析方法的正確性。該文研究給出一種計算全膠條密封車窗接觸應力和接觸長度的方法,對全膠條密封車窗結構膠條尺寸的設計具有重要指導意義。

