鐵路貨物運輸網絡關鍵節點識別算法研究
劉 杰
(重慶工程職業技術學院 智能制造與交通學院,重慶 402260)
0 引 言
鐵路貨物運輸在物流快速發展的今天扮演越來越重要的角色。在中國,鐵路占整個貨物運輸比重的8%,是全國貨物運輸的重要組成部分。貨運車站和鐵路線路構成一個龐大的鐵路貨物運輸網絡。貨運車站作為網絡中的節點,研究其重要度并找出關鍵節點對于有效保護鐵路運輸網絡安全并進一步保證貨物運輸流程通暢具有現實意義。
文獻[1]和文獻[2]分別于1998年和2000年提出小世界網絡和無標度網絡廣泛存在于現實世界,掀起了用復雜網絡理論對網絡關鍵點研究的熱潮。關鍵節點重要度識別方法多以網絡自身屬性[3]如度[4]、介數[5]和網絡效率[6]等為量化測度標準來評價網絡節點。交通研究領域主要集中在城市軌道交通拓撲結構、鐵路客運網絡和城市道路網絡方面。薛鋒等[7]利用復雜網絡理論分析了成都地鐵網絡拓撲結構,然后構建節點重要度評價指標體系并結合TOPSIS方法完成關鍵節點識別任務;諶微微等[8]構建基于二階張量的重慶軌道交通線網拓撲模型,然后用3個中心性指標評價網絡節點,結果表明,五里店、重慶西、沙坪壩和冉家壩4個站點最為關鍵;劉朝陽等[9]建立了城市軌道交通網絡級聯失效模型,并以網絡失效規模和破壞程度兩個指標對其進行評估,最后通過仿真找出網絡中的關鍵節點;陳釘均等[10]在建立鐵路網客運節點指標體系基礎上,利用粗糙集理論和主成分分析法計算客運節點綜合權重,結果表明其評判結果有效;鄧紅星等[11]選用節點度、介數和站點客流集散量等7個指標構建節點重要度評價體系,對哈爾濱市區道路網進行實證研究,結果表明,其關鍵節點識別方法可行且有效;毛劍楠等[12]在城市基礎經濟屬性、公路與鐵路客運拓撲網絡屬性和城市聯系強度屬性基礎上,提出一種城市群綜合節點重要度計算方法,以四川城市群為實證研究對象,結果表明該方法有效;宋海權等[13]定義道路重要度評價模型,并顧及路網的整體形態及路網的拓撲連通性,提出基于復雜網絡理論的路網綜合算法,對成都道路網絡實證研究結果表明該模型有效; ZHU Yanbo等[14]以圖論為基礎對絲綢之路經濟帶鐵路網絡節點重要度進行研究,利用pajek軟件仿真發現了其中3個最關鍵節點。
目前專門針對鐵路貨運網絡關鍵點識別的研究較少,僅有SUN Qipeng等[15]基于復雜網絡理論對中國鐵路貨物運輸網絡進行研究,以各省份為網絡節點、省間貨物運輸重量為邊進行建模,最后得到各節點重要度并分析了其影響因素。然而該研究只討論了以省份為節點的宏觀網絡,沒有重點討論以車站為節點的微觀網絡。人們對車站重要度更為關切。鐵路部門目前實際的做法是在分析車站客運量、貨運量和地理位置等因素基礎上,將貨運站劃分為6個等級,但這種劃分方式有很強的人為主觀性且無法量化。鐵路貨物運輸網絡的核心在于貨物的運輸特性,而不是線路的拓撲結構。貨運站每天貨物承運和卸貨情況不相同,車站間發送貨物的種類、重量也不相同。除此之外,貨物的價值也是一個影響關鍵節點識別的重要因素。顯然接收和發送貨物重量少但貨物總價值更高的車站比發送貨物重量高但價值低的車站更為重要,這是以往研究所沒有考慮的。因此筆者以貨物總價值為標準進行鐵路貨物運輸網絡節點重要度計算和關鍵節點識別研究依據。鑒于鐵路貨運網絡中的這種貨物動態轉移特性,筆者采用PageRank算法對鐵路貨運站重要度進行計算并識別關鍵點[16,17]。
1 研究方法
從微觀角度看,鐵路局所屬車站每天發送和接收的貨物運量也不盡相同,如圖1。

圖1 獨山站貨物運量Fig. 1 Dushan Station freight volume
筆者從兩個方面定義貨運車站重要度:一方面是貨運站的貨物發送和卸載業務量,業務量越大,重要度越高;另一方面是與貨運站有直接業務往來車站性質,往來車站越重要,本站重要度也越高。由于貨運車站間的貨運業務每天都在變化,同時存在一些不可控外在因素的干擾,故貨運車站每天的重要度可能都不一樣。因此,筆者定義貨運車站重要度為一個隨機變量,通過重要度算法算出車站每天的重要度構成的隨機變量樣本序列,然后擬合隨機變量的分布函數。基于車站間貨物運輸信息,可以通過PageRank算法計算得到車站每天的重要度。
基于PageRank算法計算貨運車站重要度,其核心思想是將車站抽象為圖的節點,車站間貨運業務抽象為邊,貨物運輸網絡抽象為馬爾可夫概率狀態轉移矩陣,最后采用迭代計算得到穩定解:
(1)
式中:A為概率狀態轉移矩陣;m為迭代次數;x0為節點初始重要度向量;x為最終節點重要度向量。
(2)

(3)



圖2 獨山站貨物價值Fig. 2 Value of goods at Dushan Station
(4)
式中:pg為第g種貨物價格;S為車站集合。
得到重要度樣本后,擬合各車站重要度分布函數,最后根據重要度分布函數的期望特征值計算最終的重要度數值。
2 模型建立
2.1 PageRank 算法
為了使式(2)中At在迭代中收斂,需要對原PageRank算法做出一些修改,具體算法如下[18]:
Step 1構造貨物轉移矩陣At,給定誤差閾值ε。
Step 2向該矩陣中添加虛擬節點(即設置一個虛擬車站),該節點與其他節點雙向連接,得到新矩陣:
(5)
Step 3計算轉移概率,得到概率轉移矩陣:
(6)
Step 4設初始狀態各節點重要度為[1,1,…,0]1×(n+1)(虛擬節點重要度為0),m=0,轉Step 5。



2.2 擬合分布模型選擇
有限高斯混合模型在理論上被證明可以以任意精度正逼近實數上的非負黎曼可積函數,特別可以逼近任意的概率密度函數[19]:
(7)
(8)
式中:wk為第k個單正態分布權重值;μk為第k個單正態分布均值向量;Ck為第k個單正態分布協方差矩陣;d為變量維度;K為單正態分布函數總個數。如果x為單變量,則式(8)變為:
(9)

高斯混合分布模型參數估計通常采用EM迭代算法,EM算法分為兩步,第一步稱為E-Step:
(10)

為敘述方便,整個GMM模型參數記為:
(w,μ,C)=[(wk,μk,Ck),k=1,2,…,K]
(11)
第二步稱為M-Step,其目的是最大化Q函數,如式(12),從而得到第m+1次迭代模型參數,如式(13):
(12)
wm+1,μm+1,Cm+1=argmaxQ(w,μ,C,wm,
μm,Cm)
(13)
對Q函數求導并令導數為0,可得:
(14)
(15)
(16)

重復上面第一步和第二步,直到收斂為止。
2.3 重要度計算
得到重要度分布函數后,取其均值作為車站重要度的度量,如式(17):
(17)
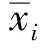
3 實例分析
數據來源于中國鐵路貨物全過程管理系統,從系統中導出中國鐵路成都局集團有限公司最近一年(即從2018年1月1日到2019年1月1日)的數據,提取其中194 d的貨運記錄觀察數據。一個車站一天貨運數據包含于承運簿和卸貨簿兩個EXCEL文件內。承運簿記錄的是該車站發往其他車站的貨物情況,內容有時間、發送目的地車站名稱、貨物名稱、計量單位和貨物重量。卸貨簿記錄的是其他車站發到本站的貨物情況,內容有時間、貨物來源車站名稱、貨物名稱、計量單位和貨物重量。筆者利用Python 3.7編程對數據進行處理[20]。經統計后得到中國鐵路成都局集團有限公司管轄貨運車站共115個,中國鐵路成都局集團有限公司與其他省市路局有貨運業務的車站總數為1 900個,因此模型參數取值為n=2 015,H=|T|=194,|G|=1 538,ε=10-6,K=30。另外,在統計中發現貨物中有用數字命名的軍用物資,比如14/65 658、18/63 678等。軍用物資涉及機密,無法知道其種類。但對于此類貨物,筆者認為其價值非常高,以一個較高單價進行計量。
根據2.1節設計的算法計算得到各車站重要度情況如圖3(僅列出5個車站重要度變化情況)。按式(16)計算得到的中國鐵路成都局集團有限公司車站重要度結果如圖4。

圖3 各車站重要度時間序列變化情況Fig. 3 Time series changes of station importance

圖4 車站重要度對比Fig. 4 Comparison of station importance
從價值標準來看,重要度前十名分別是小寨壩、彭縣、福泉、銅罐驛、巴關河、魚嘴、凱里西、廣安、新興鎮、渡口,其重要度值分別為118.28、31.1、28.87、24.54、18.45、13.23、13.04、11.69、11.46、10.46。一、二、三、四等站平均重要度分別為4.59、2.99、4.24和2.76,成都局一等站只有攀枝花站,三等站共42個,這說明三等站是整個貨運網絡中貨運重要性最高的車站集群,對三等站的保護尤其重視。從重量標準來看,重要度前10名分別是小寨壩、銅罐驛、彭縣、弄弄坪、巴關河、廣安、福泉、攀枝花、渡口、燕崗,其重要度值分別為62.27、14.07、13.55、13.15、11.8、10.86、10.69、9.86、9.56、8.42。一、二、三、四等站平均重要度分別為9.86、2.41、3.03和2.34。從兩個標準來看一等站和三等站均為貨運網絡的關鍵集群車站。小寨壩又是整個網絡最核心節點。通過分析承運簿和卸貨簿發現,排名靠前的車站如魚嘴、凱里西、新興鎮等雖然貨運量大,但是貨物價值并不高,而小寨壩、彭縣、銅罐驛除貨運量大外,周轉貨物主要是高價值集裝箱或軍用物資,這也說明了導致兩種標準差異性的原因,亦證明了結論的有效性。

4 結 語
筆者利用鐵路貨物全過程管理系統數據對中國鐵路成都局集團有限公司管轄的115個貨運車站重要度進行計算,結合PageRank算法、數據分布擬合理論計算得到了以價值和重量兩種標準下的車站重要度,同時發現了少數重要度很高的節點,這表明貨運網絡從運輸角度來看亦是一種具有少數中心節點的復雜網絡,因此對這些中心車站實施重點保護和監控尤為重要。

