能得見計算的拼圖
陳凱
“計算”一詞在不同語境下有不同的含義,即便是將范圍嚴格限定于“用機器進行自動計算”這樣狹窄的場景之中,其含義也是豐富多彩、變化多樣的。考慮這樣一個簡單的需求,計算第一項為1,且第二項為1的斐波那契數列第n項的值,如用戶輸入的是數字6,而機器給出的是對應的第6項斐波那契數列的值8,顯然,機器的確進行了計算,可要是深究其“計算”的含義,卻有如下不同。例如,機器可能只是預存了整個斐波那契數列,對于輸入的n,它實施了一個查找數據的工作。考慮人類在做8加7得15,或做8乘以7得56的計算的時候,人的頭腦事實上所做的也是這種查找數據的工作,毫無疑問這是一種計算,然而對于這個計算機器的使用者來說,它是如何查找和匹配數據的,其過程是一個黑盒,是不可見的。又如,機器可能是根據斐波那契數列的通項公式來進行計算的,而通項公式的由來,是經由觀察、歸納、假設、證明、演繹等一系列數學工作的結果,在具體使用通項公式時,數學計算本身仍然是一個黑盒,使用者還是不知道,機器是如何實現對5開方等一系列具體計算步驟的。再如,機器可能是通過一個循環結構的程序來實現計算的,它首先計算了第一項和第二項的和,并將計算結果賦予第三項,然后再計算第二項和第三項的和,再將計算結果賦予第四項,在這個過程中,除了具體的加法計算過程是黑盒,循環結構的實現本身也是一種黑盒,顯然,對于程序的編寫者來說,他不知道循環語句和結構何以能發揮作用,他只是借助這些語句和算法結構發揮了作用而已。在上述所有的例子中,對于使用計算機器的人而言,“計算”要么是全部不可見的,要么是局部不可見的。
當然,無論是為了教學,還是為了某個實際的用途,將計算機器所有的計算過程都展現出來,是不現實的,也是不必要的。例如,在用循環結構的程序計算某個斐波那契數列項的時候,人們的頭腦尚能跟蹤高級語言環境中,每個變量或數組變量中值的變化,但若要在寄存器的級別上,跟蹤用以實現循環和賦值操作的每個電信號的變化,就是相當困難的事了,更何況,求得斐波那契數列項的值只是一個很簡單的程序。若要使得解決某個具體任務的整個計算過程清晰可見,不可避免要做到以下步驟:首先,需要知道編譯程序是如何將這個高級語言程序代碼轉化成二進制機器語言的;接著,跟蹤這個二進制機器語言的執行過程,繼續往下深入,跟蹤普林斯頓結構或其他結構的計算機器中的各個部件是如何協調工作,執行這些可實現循環功能的機器代碼的;然后在更底層,了解數字電路是如何實現邏輯運算和數學運算的……如果能將整個藍圖展現出來,計算便是可見的,但顯然,即便是將很簡單的高級語言程序按上述過程全部展開,其規模也龐大到讓人的頭腦無法進行跟蹤,所以就結果而言,計算過程仍然是部分不可見的。
在工業設計上,人們采用的是模塊化和層層封裝的方式,來構造具有特定功能的計算機器。但在教學上,人們面對的是盒子里套盒子層層疊疊一時無法窮盡到底層的窘境。然而,為了理解某個問題,人的頭腦并不需要真的像機器那樣,去跟蹤所有的電信號或機械狀態的變化。因為從直觀上說,當人們發現一個小型的系統是以某種模式進行計算的之后,就能直觀推斷,一個以類似結構搭建的更大型的系統,也應該能以同樣的模式進行更大規模的計算。舉例說,計算28加7,人的思維過程是從記憶里找出8加7所對應的15,然后低位寫5,高位進1,很容易判斷,對于更大的數字,如280+70,采用的方法也是類似的,這其實就是一種模式的識別和匹配。人的頭腦能夠直觀地認識到,一個較小數字的可行的計算模式,是可以套用到更大數字上的(這里暫不討論用小規模的計算系統實現普適計算的問題,因為那涉及用一種計算模型去模擬另一種計算模型的問題)。要想讓學生理解計算之所以可行,就需要通過一個小型的計算系統的運作過程,建立起關于“計算”的直觀概念。
因此,當前的任務,就是找到一個可以進行計算的小型系統。這個系統需要滿足以下特征:一、能演示自動化的工作流程,或者稍加改造就能演示自動化的工作流程;二、運行過程能體現出計算思維的特征,如抽象化、形式化、模塊化等思想;三、運作過程是完全可見的;四、能完成某個具體任務,并且,從直觀上看,它具有經由改造后完成其他任務的潛力;五、考慮到教學資源、課時等因素,對其的講解和操作不需要依賴太多其他專業方面的知識。為了滿足以上五點要求,可供選擇的小型的計算系統范圍被大大縮小。雖然說一個小型的電子電路系統基本上也能契合上述大部分要求,但以信息技術學科“過程與控制”模塊中有限的電子電路內容看,是難以用來展現稍微復雜一些的具有計算思維特征的運作過程(如迭代、遞歸等)的。圖靈機雖然極為符合以上一到四點的要求,但若要讓學生們對其工作過程真正理解,需要耗費較多時間進行講解和操作訓練。
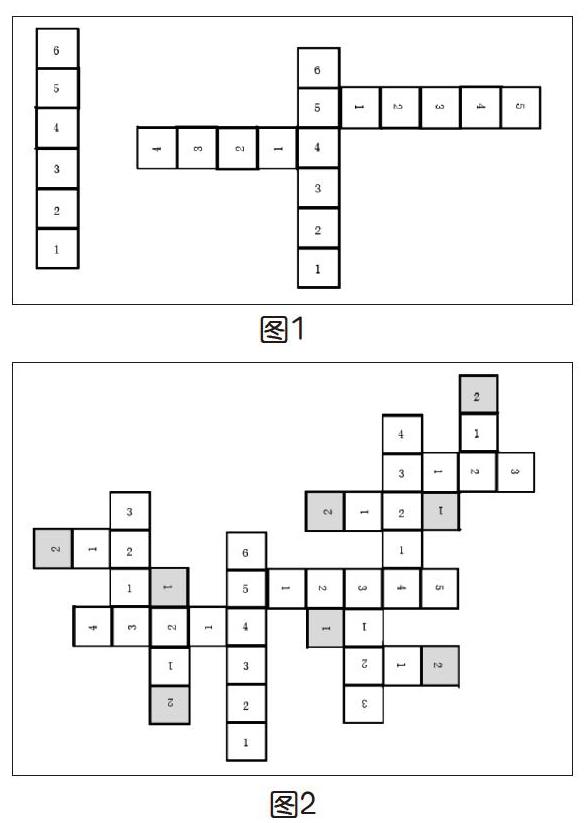
這就促使筆者設計出一種拼圖游戲來充當這樣一個小型的計算系統。游戲有很多種變化形式,下面是一個可計算斐波那契數列項的拼圖游戲,拼圖是一些不同長度的條狀紙片,紙片上分出格子并按自然數順序標上數字。每個拼圖就好像太空站一樣,在最大數字的格子的下方兩個格子上各留出了兩個對接接口,用于拼接那些最大數字和格子號碼相同的拼圖。拼圖的最大數字是n,則接口的位置在n-1和n-2處。例如,對有6個格子的拼圖,接口位置在5號格子和4號格子的位置,5號格子可以拼5個格子的拼圖,4號格子可以拼4個格子的拼圖。如果按這樣的模式匹配,則計算過程一直能進行下去,直到所有的“空間艙”都無法滿足繼續拼接的要求,也就是說,不再能找到可匹配的模式,計算過程自然而然就停止了。顯然,拼接工作終止于最大數字是2或者1的拼圖。圖1顯示了拼圖的第一步,圖2顯示了完成后的整個拼圖。
當每次使用到最大數字是2或是1的拼圖時,可以用作標記的方法計數一次,可以看到,如果最初使用的拼圖的最大數字是6,則整個拼圖完成后,計數值是8。這其實就是計算了第6項的斐波那契數列的值為8。整個過程對應用遞歸的方法來計算斐波那契數列的過程:為了計算第n項的斐波那契數列的值,則需要先計算第n-1項和第n-2項的斐波那契數列的值,此過程一直持續下去直到遇見第二項和第一項的斐波那契數列的值為1。可以看出,拼圖游戲能體現出解決具體問題中計算思維的特征,整個運作過程是完全可見的,拼接過程中并不涉及其他專業知識。雖然說拼圖過程并不是全自動化進行的,但一旦規則設定好,即便是手工操作,其結果也是必然的。這里可以鼓勵學生對拼圖進行改進,如留出特定寬度的拼接凹凸接口,這樣,即便不對照數字的大小,也能將拼接過程進行下去。
拼圖游戲的一個很重要的優勢是,拼接規則是可以方便地進行擴充和改造的。不妨思考這樣的問題,如果設計一臺計算機器,那么它將如何自動完成圖形的拼接,并由此實現斐波那契數列項的計算?關于自動機器實現拼接過程中可能遇到的麻煩,以及如何使得自動拼接成為可能,可以開展一次頭腦風暴活動。關于機器實現自動拼接中的困難,這里試舉一項:計算機中比較容易實現的數據存儲方式,是一系列前后相鄰的存儲單元,于是就產生出問題,即二維空間上的拼圖,如何轉化為一維的數據存儲方式。
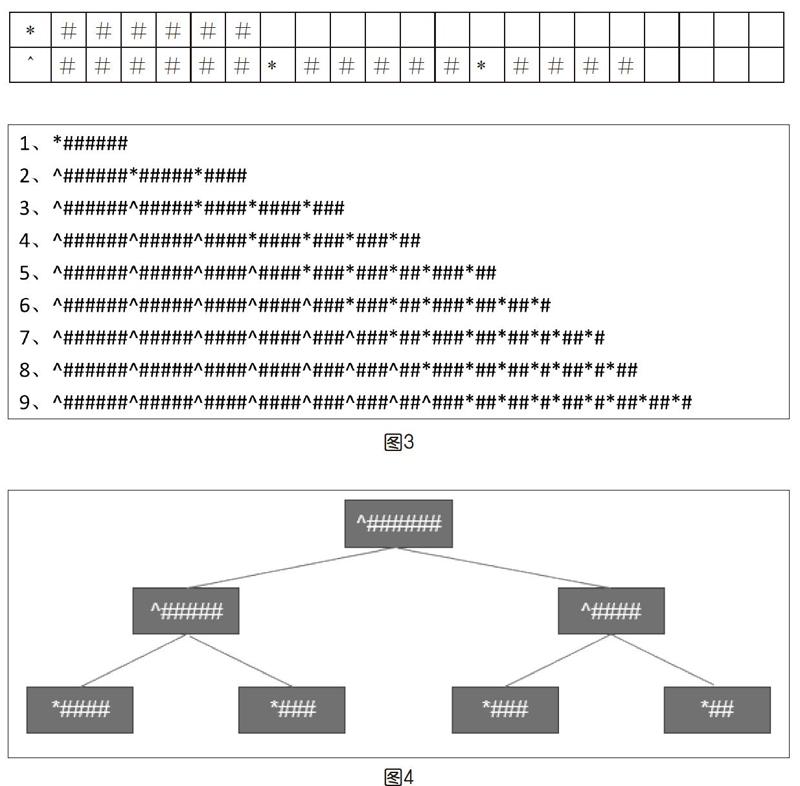
顯然,在一維的數據存儲空間中,拼接過程要通過符號模擬來達成。具體方案很多,如用“#”代表拼圖,“*”代表等待拼接,“^”代表拼接完成,一種可能的操作規則和操作過程如下表所示。
下表表示了6個格子的拼圖拼接上5個格子和4個格子的拼圖的過程,每次拼接完成后,“*”變為“^”符號,表示處理完成。整個拼接過程中,總是按遇見n個格子則在最后拼接n-1個格子和n-2個格子的規則進行,如果遇見的是2個格子和1個格子的拼圖,則只是簡單拼接上和自己相同數量的格子的拼圖(為了簡化問題,這個匹配過程沒有考慮停機問題,可以引入新的符號來實現停機的匹配規則),整個變化過程用字符串描述如圖3所示。
第9步之后,拼圖中“*”的數量不會再發生變化,而“*”的個數則對應著相應第6項斐波那契數列的值。并且,還能有辦法看出不同拼圖之間的關系:第1塊拼圖拼接的是第2和第3塊,第2塊拼接的是第4和第5塊,第3塊拼接的是第6和第7塊,以此類推。當然,這樣的表示方法很不直觀,如果以樹的形狀將拼圖之間的關系呈現出來,則要清晰得多,圖4是第4步拼接操作完成時所顯示出的拼圖之間的關系。于是這里又引出了新的問題,如何能更合理地借助一維的存儲空間,使得機器能方便地識別出拼圖之間的關系,同時,也能讓人更容易將存儲空間里的數據轉換成人更能理解的圖示?這就很自然地從如何實現自動計算的問題,指向了數據結構的研究。
至此我們可以看出,借助拼圖游戲,不僅使得計算的過程變成可見的,而且也使得自動計算中,解決問題的思維方式成為可見的。關于如何使計算過程可見,進而如何使計算思維可見,方法必然有很多種,本文權當拋轉引玉,希望能激發出大家的思考欲望。

