2.5維編織復合材料經向拉伸彈性性能預測

李居影，李瑩，王榮惠，魏化震，孔國強

(中國兵器工業集團第53研究所, 山東 濟南 250031)

0 引言

目前，火箭發動機噴管擴散段燒蝕層主要采用高溫模壓成型的短切碳纖維增強酚醛復合材料。該復合材料具有耐強沖刷燒蝕能力較好、成型工藝簡單等優點。但是發動機在連續長時或間歇條件下工作時，擴散段燒蝕層易產生開裂、分層，甚至出現大面積整體脫落的現象，嚴重影響了發動機工作的安全性能[1-3]。

2.5維編織復合材料具有高強度、高模量、高損傷容限、耐沖擊、抗分層和抗疲勞等綜合性能，其經緯紗交織結構可以明顯改善復合材料層間性能弱的缺點，越來越受到人們的關注[4-7]。但是2.5維編織織物在織造過程中因經緯紗彎曲交聯影響織物及其復合材料的力學性能[8-9]，如何設計和優化2.5維編織織物及其復合材料的力學性能成為研究熱點。

董偉峰[10]針對2.5維彎聯編織復合材料，采用經向纖維束的雙凸透鏡形，且其中心線沿正弦曲線排布的假設，建立了一種新的有限元模型，并對其彈性常數進行預測，并與試驗值進行對比，表明了該有限元模型的正確性。朱永新等[11]采用沿經向切片積分的方法計算2.5維編織復合材料的宏觀經向拉伸彈性模量，經紗彎曲程度較小的直聯結構和添加平直經紗的襯經結構能夠有效提高2.5維編織復合材料的經向拉伸彈性模量，并且能夠改善經向拉伸應力-應變曲線的非線性。隨著有限元計算方法的發展，Cox等[12]、Xu等[13]、Meglockton等[14]、王新峰[15]、孔春元等[16-17]用有限元方法對2.5維機織復合材料的彈性力學性能進行了計算。

本文采用非線性多尺度材料設計與分析方法，首先輸入碳纖維性能參數、樹脂基體力學性能參數，創建2.5維編織復合材料的纖維和樹脂基體組成相，然后輸入編織工藝參數建立復合材料的代表性體積元(RVE)模型，并于一端固定約束，另一端施加準靜態拉伸載荷，得到其經向彈性拉伸應力-應變曲線及其應力、應變分布情況。進行彎聯結構和直聯結構的2.5維編織復合材料試樣制備及其拉伸性能表征試驗，獲得兩種復合材料的拉伸應力-應變曲線及其拉伸模量等數據，并將試驗結果與仿真計算結果進行對比分析，從而驗證了非線性多尺度材料設計與分析方法的有效性。

1 RVE模型的建立

建立2.5維編織復合材料RVE模型是進行仿真計算的基礎。本文以國產T800/6k級碳纖維制備的2.5維編織織物為增強體，以含硅芳炔(PSA)樹脂為基體制備的2.5維編織復合材料作為仿真計算的初始研究對象。根據國產T800/6k級碳纖維性能參數如密度、縱向彈性模量、橫向彈性模量、剪切模量、泊松比等，以及樹脂基體性能參數如密度、楊氏模量、泊松比等，建立2.5維編織復合材料的纖維增強體和樹脂基體等細觀結構的組成相，性能參數如表1所示。

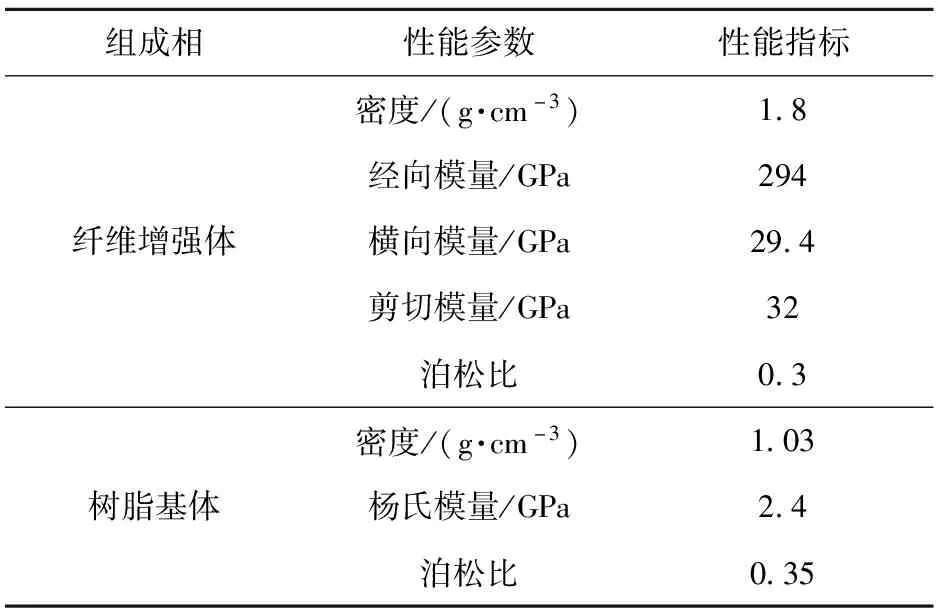
表1 2.5維編織復合材料組成相性能參數

在2.5維編織復合材料纖維增強體和樹脂基體等細觀結構組成相建立的基礎上，按照表2所示的2.5維編織織物的工藝參數，分別構建彎聯結構和直聯結構的2.5維編織復合材料RVE模型。

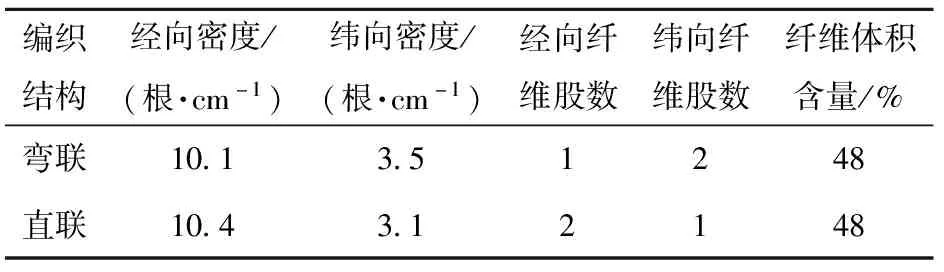
表2 2.5維編織織物的工藝參數

圖1和圖2分別為兩種結構2.5維編織復合材料RVE模型，其中紅色紗線代表經向纖維(經紗)，藍色紗線代表緯向纖維(緯紗)。比較圖1和圖2可以看出：彎聯編織復合材料織物的經紗與緯紗交織點較多，經紗屈曲較大，經紗的浮長較短；直聯編織復合材料織物的經紗與緯紗交織點稀疏，經紗屈曲較小，經紗的浮長稍長。

圖1 彎聯2.5維編織復合材料RVE模型

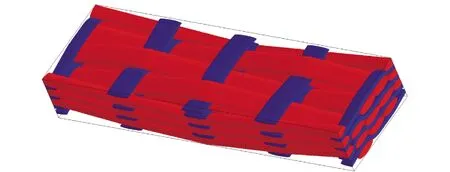
圖2 直聯2.5維編織復合材料RVE模型

分別對上述兩種結構2.5維編織復合材料的RVE模型進行有限元網格的劃分，結果分別如圖3和圖4所示。

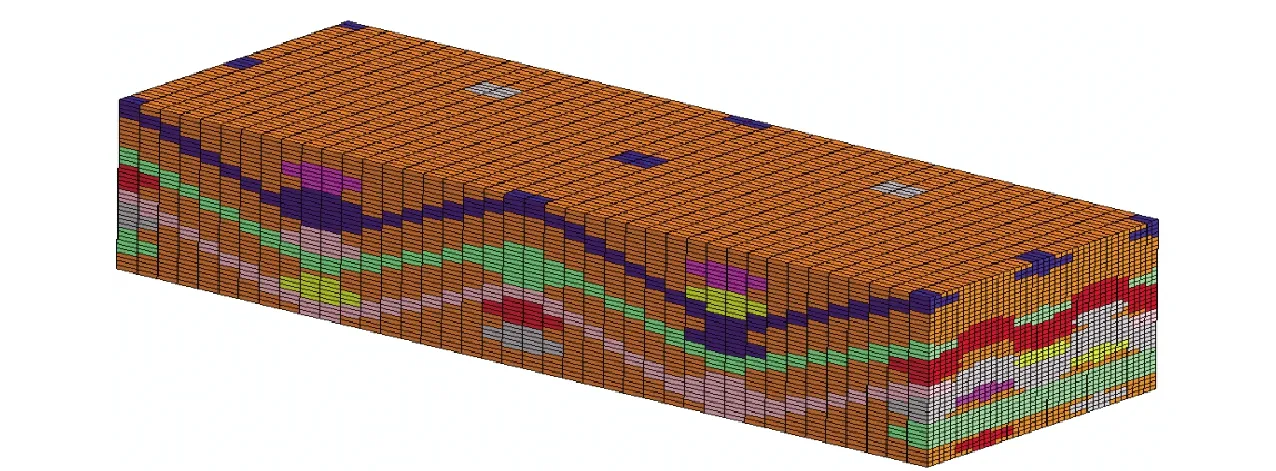
圖3 彎聯2.5維編織復合材料RVE模型有限元網格圖

圖4 直聯2.5維編織復合材料RVE模型有限元網格圖

2 RVE模型仿真計算

為得到兩種結構2.5維編織復合材料RVE模型的經向拉伸彈性性能，對建立的2.5維編織復合材料RVE模型進行仿真計算。在進行具體的仿真計算工作前作如下假設：

1)假定樹脂基體在本次準靜態拉伸工況下(RVE模型單元最大拉伸應變為1%)，僅表現出彈性性能。

2)假定纖維與樹脂界面的結合完好，暫不考慮界面性能對復合材料整體性能的影響。

3)假定纖維絲束在編織過程中無任何初始損傷，無纖維絲折斷等現象。

基于上述假設，利用非線性多尺度材料設計與分析軟件，進行兩種結構2.5維編織復合材料RVE模型的經向拉伸彈性性能預測。

首先將2.5維編織復合材料RVE模型一端施加固定約束，另一端施加準靜態拉伸載荷(拉伸應變設為1%)，拉伸方向沿2.5維編織復合材料的經紗方向(經向)。通過仿真計算得到2.5維編織復合材料RVE模型的平均彈性拉伸應力-應變曲線及其在復合材料模型內部的分布云圖。

圖5為仿真計算得到的彎聯結構2.5維編織復合材料平均彈性拉伸應力-應變曲線。從圖5中可以看出，對于彎聯結構的2.5維編織復合材料RVE模型，當經向彈性拉伸應變達到1%時，經向彈性拉伸應力達到了265 MPa，計算得知其經向拉伸彈性模量為26.5 GPa.

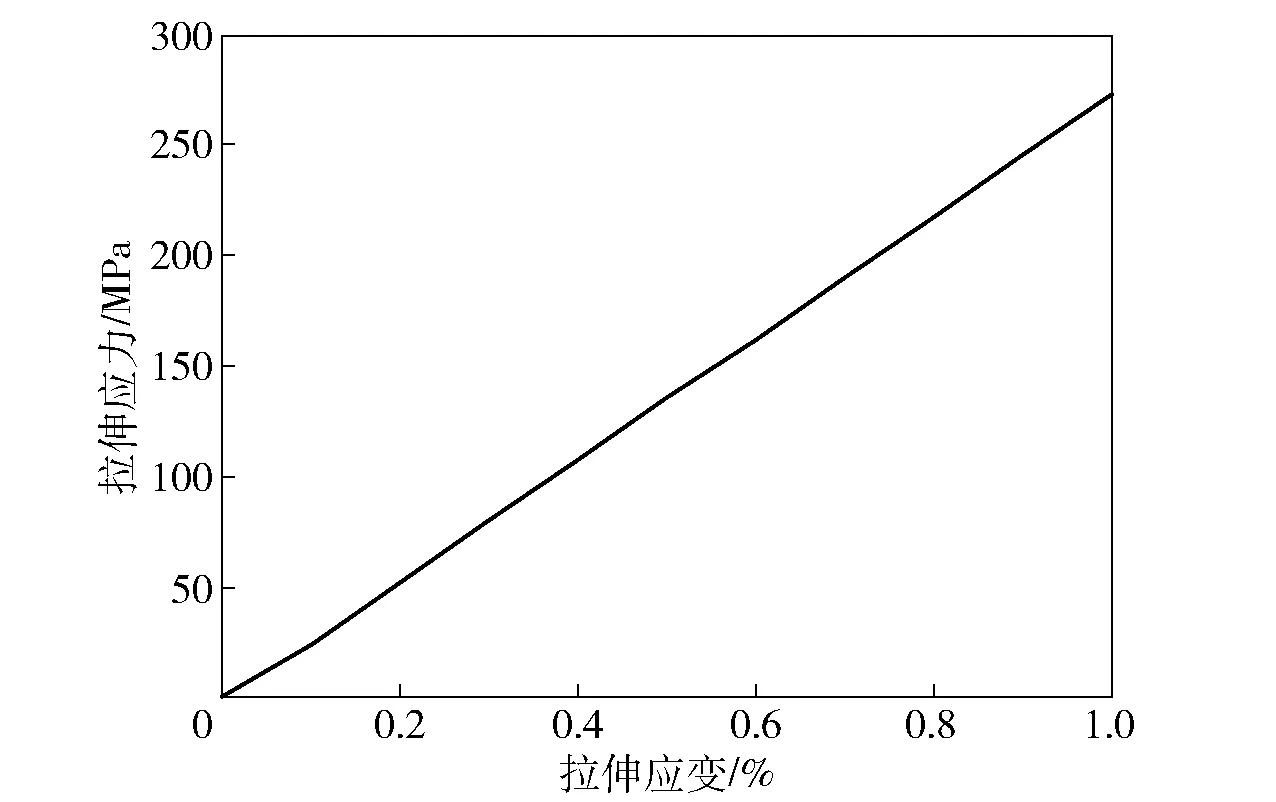
圖5 彎聯2.5維編織復合材料RVE模型的經向彈性拉伸曲線

圖6為仿真計算得到的直聯結構2.5維編織復合材料平均彈性拉伸應力-應變曲線。從圖6中可以看出，對于直聯結構的2.5維編織復合材料RVE模型，當經向彈性拉伸應變達到1%時，經向彈性拉伸應力達到了1 060 MPa，計算得知其經向拉伸彈性模量為106 GPa.

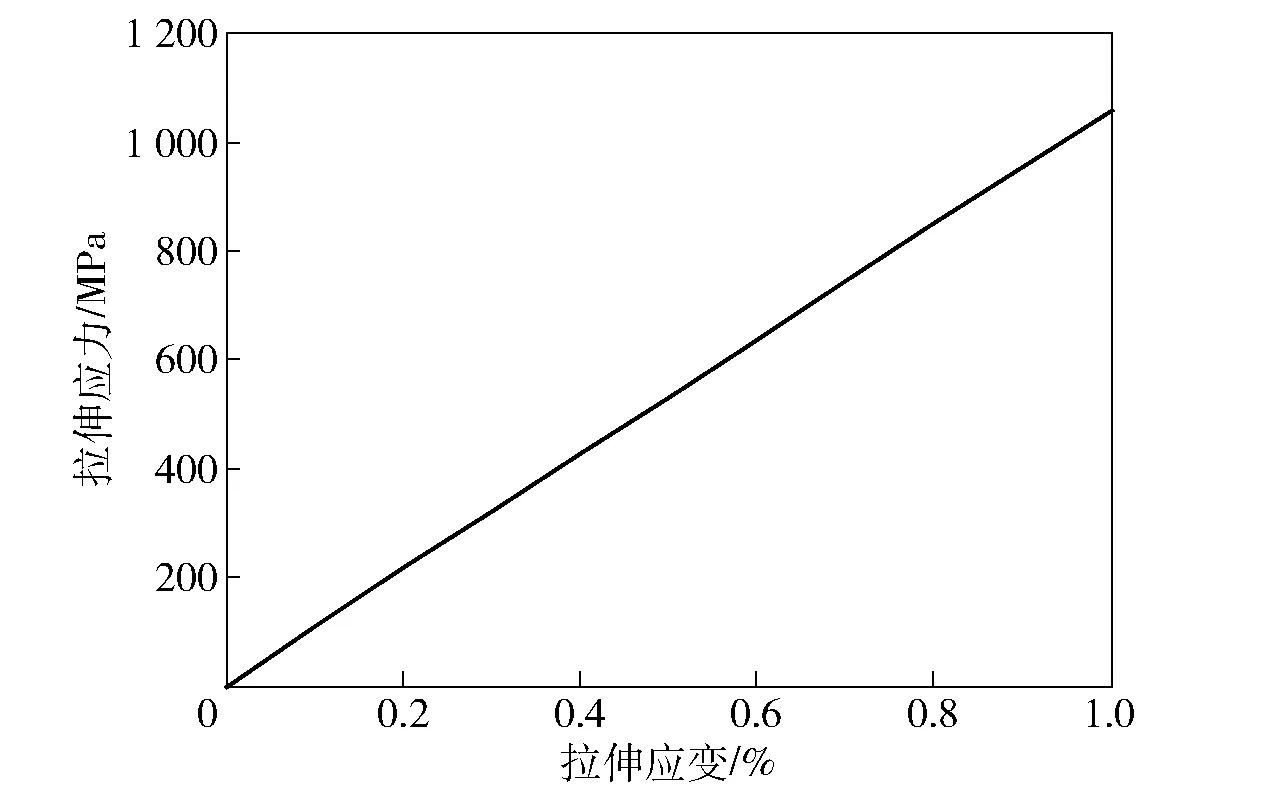
圖6 直聯2.5維編織復合材料RVE模型的經向彈性拉伸曲線

圖7為仿真計算得到的彎聯結構2.5維編織復合材料RVE模型的經向彈性拉伸應力分布云圖。從圖7中可知，當彈性拉伸應變達到1%時，RVE模型內最大應力達到1.51 GPa，且應力較高點主要分布在經紗伸直處，即經紗與緯紗相交區域，緯紗及樹脂內的應力水平較低。圖8為仿真計算得到的彎聯結構2.5維編織復合材料RVE模型彈性拉伸應變分布云圖。

圖7 彎聯2.5維編織復合材料RVE模型的彈性拉伸應力云圖

圖8 彎聯2.5維編織復合材料RVE模型的彈性拉伸應變云圖

從圖8中可知，模型的最大主應變達到3.3%(本計算過程中暫不考慮破壞)，最大主應變分布在經紗傾斜處，即相鄰緯紗區域。初步預測認為，對于彎聯結構2.5維編織復合材料RVE模型，當其受到經向拉伸應力破壞時，拉伸破壞首先在相鄰緯紗之間出現。圖9為仿真計算得到的直聯結構2.5維編織復合材料RVE模型彈性拉伸應力分布云圖。

圖9 直聯2.5維編織復合材料RVE模型的彈性拉伸應力云圖

從圖9中可知，當拉伸應變達到1%時，RVE模型內最大應力達到3.21 GPa，且應力在經向紗線內分布較為均勻。圖10為仿真計算得到的直聯結構2.5維編織復合材料RVE模型的彈性拉伸應變分布云圖。

圖10 直聯2.5維編織復合材料RVE模型的彈性拉伸應變云圖

從圖10中可知，RVE模型的最大主應變達到3.7%(本計算過程中暫不考慮破壞)，最大主應變分布在經紗彎曲最大處，即經紗與緯紗相交區域。初步預測認為，對于直聯結構2.5維編織復合材料RVE模型，當受到經向拉伸應力破壞時，拉伸破壞首先在經紗彎曲最大處出現。

3 2.5維編織復合材料經向拉伸試驗驗證

為了驗證上述兩種結構2.5維編織復合材料RVE模型仿真預測的彈性拉伸模量及拉伸破壞形式準確性，按照國家標準GB/T 1447—2005纖維增強塑料拉伸性能試驗方法進行彎聯結構和直聯結構2.5維編織復合材料試樣的經向拉伸性能表征，計算得到了相應復合材料的拉伸彈性模量等試驗數據，并獲得了兩種結構2.5維編織復合材料試樣的拉伸應力-應變曲線和拉伸破壞形貌圖片。將試驗結果與仿真結果進行對比分析，從而驗證了2.5維編織復合材料RVE模型仿真方法對復合材料拉伸彈性模量和拉伸破壞形式預測方面的有效性。圖11為彎聯結構2.5維編織復合材料的拉伸應力-應變仿真結果和試驗結果。

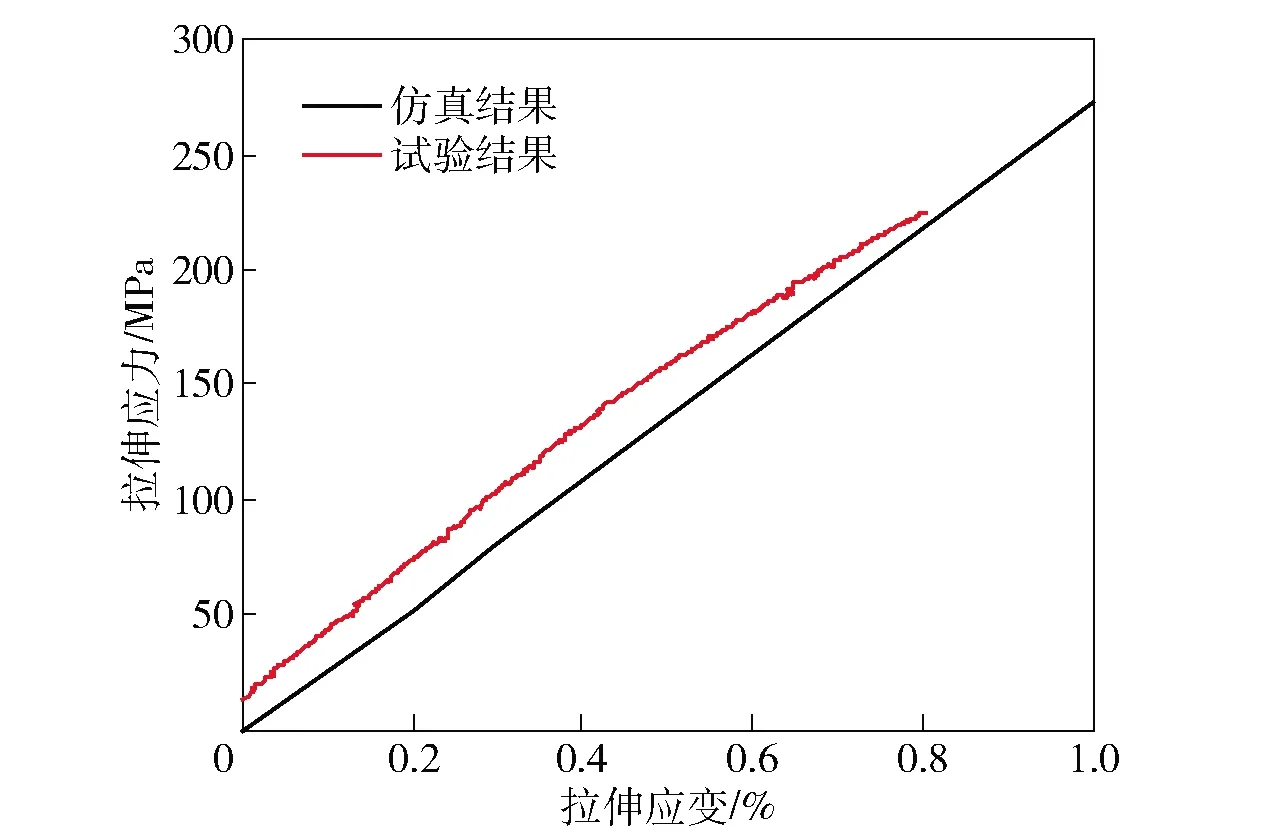
圖11 彎聯2.5維編織復合材料的拉伸應力-應變曲線

由圖11仿真結果可以看出，在0～1%的拉伸應變范圍內，該曲線表現出了明顯的彈性拉伸特征。分析認為，該彈性拉伸特征主要是由第2節設定的3個仿真計算假設決定的。由圖11試驗結果可以看出：在0～0.4%的拉伸應變范圍內，該曲線表現出了較為明顯的彈性拉伸特征；在大于0.4%的拉伸應變范圍，該曲線卻表現出了較為明顯的塑性拉伸特征。分析認為，試驗曲線由彈性拉伸階段向塑性拉伸階段轉變主要是由于樹脂基體與纖維的斷裂以及樹脂基體與纖維基體之間界面的逐漸破壞造成的。

通過比較圖11的仿真結果和試驗結果還可以看出，兩曲線在0～0.4%的彈性拉伸應力-應變過程中吻合度一般，當拉伸應變大于0.4%時，兩曲線吻合度趨好。

圖12為直聯結構2.5維編織復合材料的拉伸應力-應變的仿真結果和試驗結果。由圖12仿真結果可以看出，該曲線和彎聯結構2.5維編織復合材料拉伸應力-應變計算曲線極為相似，在0～1%的拉伸應變范圍內，表現出明顯的彈性拉伸特征。由圖12試驗結果可以看出，在0～0.6%的拉伸應變范圍內，該曲線表現出明顯的彈性拉伸特征，在大于0.6%的拉伸應變范圍，表現出明顯的塑性拉伸特征。

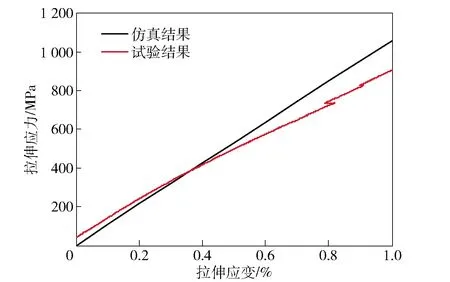
圖12 直聯2.5維編織復合材料的拉伸應力-應變曲線

通過比較圖12中的仿真結果和試驗結果可以看出，兩曲線在0～0.6%的彈性拉伸應力-應變過程中吻合度較好，當拉伸應變大于0.6%時，兩曲線吻合度變差。

通過比較圖11和圖12的試驗結果可知，圖12中試驗結果的彈性拉伸應變范圍更大。分析認為，這主要是因為直聯結構2.5維編織織物中沿經紗方向的纖維伸直度比彎聯編織織物的伸直度好，經紗與緯紗屈曲降低，而且經紗的浮長增加，在經向拉伸方向上對2.5維編織復合材料力學性能的貢獻率更高。這種較為平直的經向纖維編織結構導致了復合材料中樹脂基體、纖維以及樹脂基體與纖維之間界面的斷裂破壞行為延后，相應的曲線彈性應變范圍增加[18-19]。

為進一步驗證兩種結構2.5維編織復合材料在彈性拉伸應力-應變過程中的吻合度差異，進行兩種結構2.5維編織復合材料經向拉伸彈性模量試驗數據采集，并與仿真計算數據進行對比分析。表3為兩種結構2.5維編織復合材料在彈性拉伸應力-應變過程中經向拉伸彈性模量的仿真結果和試驗結果。

由表3可以看出：對于彎聯結構2.5維編織復合材料，在0～0.4%彈性拉伸應變范圍內，其經向拉伸彈性模量仿真計算值和試驗測試值的CV值為16.7%，其值超過15%，結果表明，RVE模型仿真計算方法不適用于彎聯結構2.5維編織復合材料經向彈性拉伸模量預測；對于直聯結構2.5維編織復合材料，在0～0.6%彈性拉伸應變范圍內，其經向拉伸彈性模量仿真計算值和試驗測試值的CV值僅為3.1%，對比分析認為，采用2.5維編織復合材料RVE模型仿真計算方法可以比較準確地對直聯結構2.5維編織復合材料的經向拉伸彈性模量進行預測。

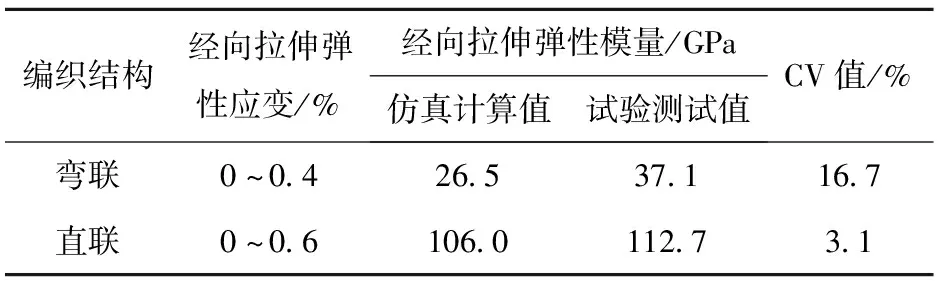
表3 2.5維編織復合材料經向拉伸彈性模量

由表3還可以看出，直聯結構2.5維編織復合材料經向拉伸彈性模量高于彎聯結構2.5維編織復合材料，前者約為后者的3～4倍。

為進一步驗證RVE模型仿真計算方法對2.5維編織復合材料拉伸破壞形式預測的準確性，對兩種結構2.5維編織復合材料試樣進行了拉伸性能測試和拉伸斷裂形貌圖像采集，并與通過仿真計算彈性拉伸應變云圖預測的復合材料拉伸破壞形式進行對比分析。

圖13為彎聯結構的2.5維編織復合材料試樣的拉伸斷裂形貌照片及其對應的相同結構2.5維編織復合材料RVE模型彈性拉伸應變云圖。圖13中單向紅色箭頭表示經向纖維方向，雙向紅色箭頭表示復合材料試樣斷口位置及斷裂方向。由圖13(a)可以看出，彎聯結構2.5維編織復合材料試樣的拉伸斷面比較齊整，斷裂纖維為處于兩相鄰緯向纖維之間的經向纖維絲束，斷裂形式為貫穿式整體斷裂，斷裂方向沿緯向纖維方向。由圖13(b)可以看出，該相同結構復合材料RVE模型彈性拉伸應變云圖的最大彈性主應變分布在兩相鄰緯向纖維(藍色區域)之間(圖中的黃色區域)，即第2節預測的復合材料RVE模型的最先斷裂位置。

圖13 彎聯2.5維編織復合材料的拉伸破壞及預測

通過以上對比可知，對于彎聯結構2.5維編織復合材料，其經向拉伸斷裂特性如斷裂位置、斷裂方向的試驗結果和仿真計算預測結果非常吻合。分析認為，采用2.5維編織復合材料RVE模型仿真計算方法能夠比較準確地對彎聯結構2.5維編織復合材料拉伸斷裂形式進行預測。

圖14為直聯結構2.5維編織復合材料試樣的拉伸斷面形貌照片及其對應的相同結構2.5維編織復合材料RVE模型彈性拉伸應變云圖。圖14中單向紅色箭頭表示經向纖維方向，雙向紅色箭頭表示復合材料試樣斷口位置及斷裂方向。由圖14(a)可以看出，直聯結構2.5維編織復合材料拉伸試樣出現了與經向纖維方向呈約30°夾角的拉伸裂紋，無貫穿式拉伸斷面產生。由圖14(b)可以看出，直聯結構2.5維編織復合材料RVE模型彈性拉伸應變云圖的最大彈性主應變出現在經向纖維彎曲最大處(紅色區域，經向纖維和緯向纖維相交位置)，即第2節預測的復合材料RVE模型的最先斷裂位置。通過對出現的經向纖維彎曲最大處(紅色區域)進行連線，連線方向(雙向紅色箭頭)基本與經向纖維方向(單向紅色箭頭)呈約30°夾角。

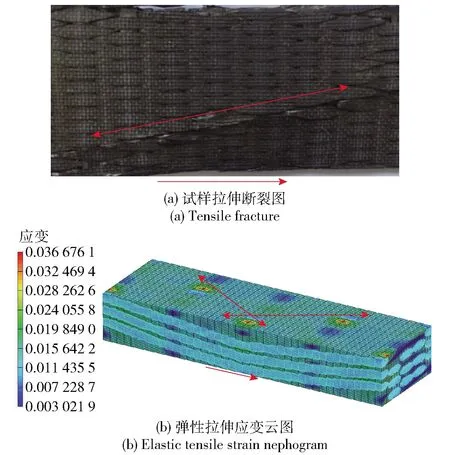
圖14 直聯2.5維編織復合材料的拉伸破壞及預測

通過以上對比可知，對于直聯結構2.5維編織復合材料，其經向拉伸斷裂特性如斷裂位置、斷裂方向的試驗結果與仿真結果非常吻合。分析認為，采用2.5維編織復合材料RVE模型仿真計算能夠比較準確地對直聯結構2.5維編織復合材料拉伸斷裂形式進行預測。

4 結論

本文采用非線性多尺度材料設計與分析方法，進行了彎聯和直聯兩種結構2.5維編織復合材料RVE模型的經向拉伸彈性性能仿真計算，并對RVE模型進行了經向拉伸彈性模量和拉伸破壞形式的預測。同時進行了兩種結構2.5維編織復合材料試樣的經向拉伸性能表征，并與仿真計算的預測結果進行對比分析。得出主要結論如下：

1)采用非線性多尺度材料設計與分析方法，通過2.5維編織復合材料RVE模型仿真計算，可以比較準確地對直聯結構2.5維編織復合材料的經向拉伸彈性模量進行預測，其仿真計算值和試驗測試值的CV值僅為3.1%；對于彎聯結構2.5維編織復合材料，其仿真計算值和試驗測試值的CV值超過了15%，表明該計算方法不適用于彎聯結構2.5維編織復合材料的經向拉伸彈性模量預測。

2)采用非線性多尺度材料設計與分析方法，通過復合材料RVE模型的彈性拉伸應變云圖，可以比較準確地對兩種結構2.5維編織復合材料的拉伸斷裂形式進行預測。

3)仿真結果和試驗測結果均表明，直聯結構2.5維編織復合材料的經向拉伸彈性性能要遠優于彎聯結構2.5維編織復合材料，其中直聯結構2.5維編織復合材料經向拉伸彈性模量約為彎聯結構的3～4倍。