基于深度學習的壓縮感知FDD 大規模MIMO 系統稀疏信道估計算法

黃源，何怡剛,2，吳裕庭，程彤彤，隋永波，寧暑光

（1.合肥工業大學電氣與自動化工程學院，安徽 合肥 230009；2.武漢大學電氣工程學院，湖北 武漢 430072）

1 引言

由于頻譜利用率高、波束成形增益大的優點，大規模多輸入多輸出（MIMO,multi-input multi-output）技術被認為是未來無線通信中的關鍵使能技術之一[1-5]。在FDD（frequency division duplexing）大規模MIMO 系統的下行鏈路中，準確的信道狀態信息對波束成形至關重要。隨著基站端天線數不斷增加，通信系統矩陣規模日益復雜，精確的FDD 大規模MIMO 系統稀疏信道估計成為挑戰性的問題。

傳統的線性大規模MIMO 系統信道估計算法包括最小二乘（LS,least square）算法[6]和最小均方誤差（MMSE,minimum mean square error）算法[7]等。其中，LS 采取偽逆求解的算法，性能較差；MMSE 通過計算信道的二階統計量，性能得到了較大提高。然而，這些算法均需要較多的導頻資源才能準確地估計信道，因此頻譜資源利用率較低。

近年來，研究人員通過對信道進行研究發現無線多徑信道在時域、頻域和空域中均存在稀疏特性[8]。通過挖掘信道的稀疏特性，應用壓縮感知（CS,compressed sensing）相關理論實現一種有效的信道估計算法已成為當下研究的熱點。基于無線信道所具有的時域稀疏特性，文獻[9]提出了一種改進的正交匹配追蹤（OMP,orthogonal matching pursuit）算法，以降低導頻開銷，提高信道估計精度。對于FDD模式下的大規模MIMO系統下行信道估計，文獻[10]采用壓縮感知技術來減少信道估計訓練和反饋過程中的資源開銷，并利用用戶信道矩陣中的聯合稀疏性，提出了一種分布式壓縮感知信道估計方案，即聯合正交匹配追蹤（JOMP,joint orthogonal matching pursuit）算法。該算法可以通過用戶端獲取的壓縮信號使基站端完成信道的精確估計。為了擺脫OMP 算法對信道稀疏度的先驗條件的依賴，文獻[11]提出了一種應用于具有時間相關性的MIMO-OFDM 系統的改進稀疏自適應匹配追蹤（SAMP,sparsity adaptive matching pursuit）算法。在不需要獲得信道稀疏度先驗知識的情況下，該算法能夠完成信道重構過程中對支撐集的自適應選擇，從而提高信道估計的性能。文獻[12]在SAMP 算法的基礎上進一步提出了一種基于塊稀疏共軛梯度自適應匹配追蹤（BSBCG-SAMP,block sparsity based conjugate gradient SAMP）算法。該算法考慮了時延域大規模MIMO 信道的時空公共稀疏性，能夠自適應地獲取信道結構化稀疏矩陣的稀疏度。雖然BSBCG-SAMP 精度較高，但是其在迭代過程中受信道噪聲的影響較大。在噪聲環境中，該算法的估計性能會急速下降。然而，這些算法大多采用結構化稀疏特性對無線信道進行估計，利用迭代優化策略求解欠定最優化問題。這些重構算法的弱點是收斂速度慢。該弱點將CS 技術限制在非實時場景的應用中，并且這種迭代優化的密集計算已成為CS在無線信道估計應用中的瓶頸。

為了進一步提高信道估計的精度和解決CS 算法在實時場景中應用的問題，本文針對FDD 大規模MIMO 下行鏈路提出了一種基于深度學習的CS稀疏信道估計算法，即卷積重構網絡（ConCSNet,convolutional compressive sensing network）。該算法的主要思想是在沒有稀疏度的前提下，采用數據驅動的方法，通過卷積神經網絡求解從測量向量y到信號h的逆變換過程，從而解決CS 框架下的欠定最優化問題，并實現對原始信道的重構。其次，該算法采取離線訓練和在線學習的模式，實現對無線信道的實時估計。實驗結果表明，與傳統的基于貪婪算法的壓縮感知稀疏信道估計算法相比，本文提出的ConCSNet 算法精度較高，且運算速度較快。

2 系統模型

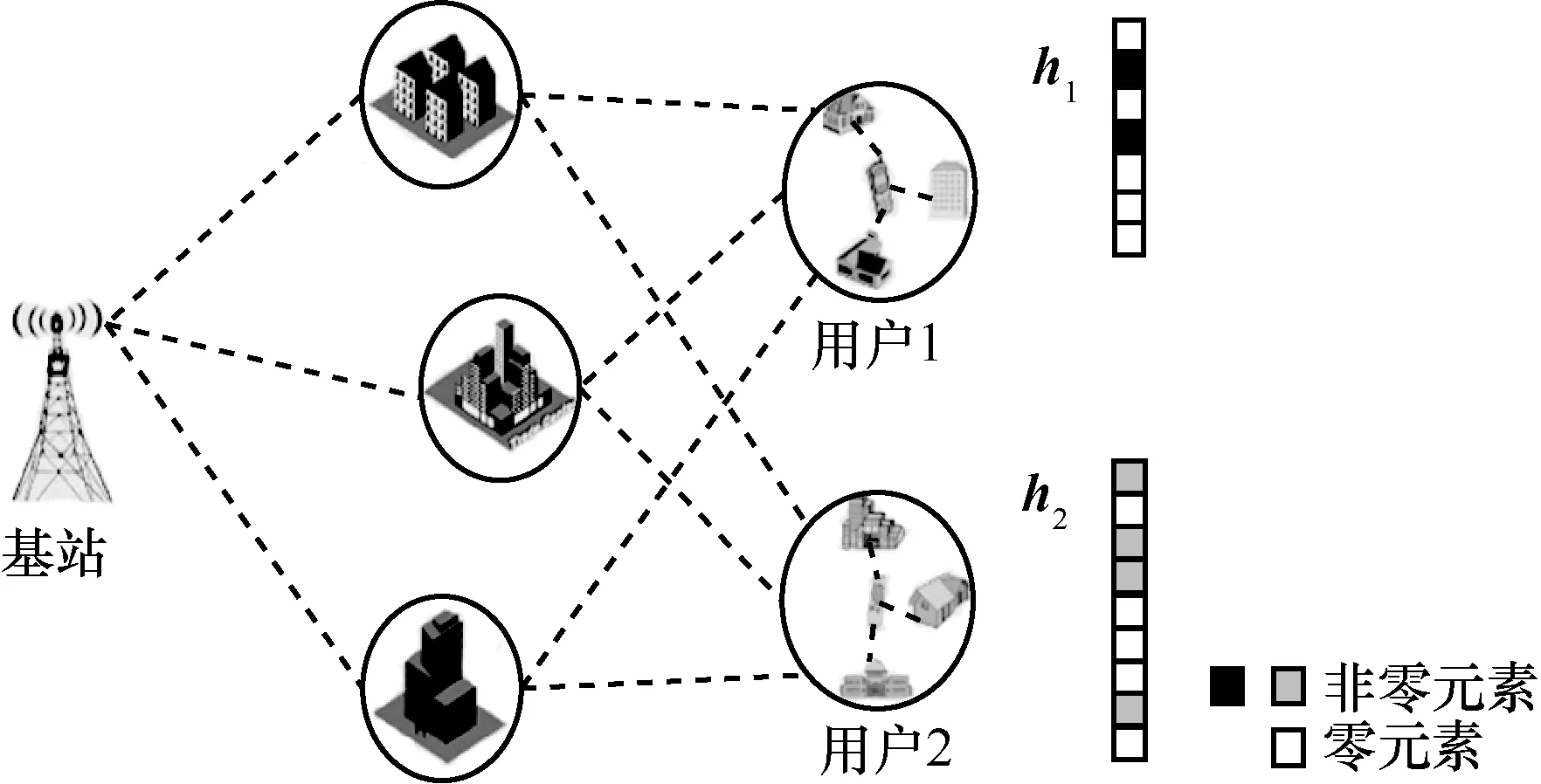
圖1 基站與移動端散射信號示意

該系統具有NT根發射天線，NR根接收天線和N個子載波。發射信號經過頻率選擇性衰落信道到達接收端，假設信道參數在一個OFDM 符號中為常量，信道長度為L。該系統具有W個導頻符號，并且分別位于子載波k1,k2,…,kW上。第n根接收天線所接收到的信號可以表示為

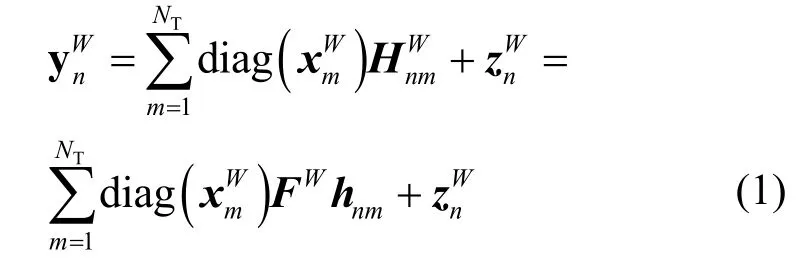
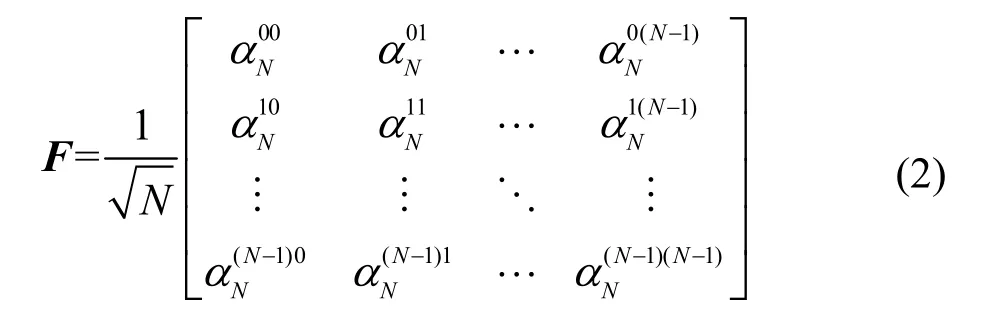
令FW為F中對應的W行和前L列組成的W×L維矩陣，為信道的時域脈沖響應矩陣。時域多徑信道hnm通常呈現稀疏特性，即大部分能量集中在少量信道抽頭上，而其余小部分能量分布低于噪聲門限，且信道非零抽頭數目遠小于信道長度L。hnm可以表示為

3 基于傳統貪婪算法的壓縮感知稀疏信道估計算法

由式(5)可知，接收信號y的長度遠小于信道h的長度，即NRW?NRNTL。因此，式(5)是一個欠定方程，存在無窮多個解，難以重構原始信道h。然而，根據CS 的相關理論可知[13]，當原始信號是K稀疏的，并且y與T滿足有限等距準則（RIP,restricted isometry property）時，原始信號可以由測量值y通過求解最優l0范數問題精確重構。因此，稀疏度為K的信道h可以通過求解一個欠定最優化問題，然后從包含NRW個測量值的信號y中得到完美的重構，即

其中，ξ為噪聲方差。值得注意的是，當導頻是高斯隨機矩陣時，觀測矩陣T滿足有限等距約束準則。許多基于傳統貪婪算法的壓縮感知稀疏信道估計算法相繼被提出，并不斷完善式(6)的求解方法和重構性能，如正交匹配追蹤OMP 算法[9]、稀疏自適應匹配追蹤SAMP 算法[11]、壓縮采樣匹配追蹤（CoSaMP,compressive sampling matching pursuit）算法[14]和廣義正交匹配追蹤（gOMP,generalized orthogonal matching pursuit）算法[15]。

基于傳統貪婪算法的壓縮感知信道估計算法原理如圖2 所示。該算法首先通過感知矩陣T對稀疏信道h進行壓縮采樣，然后利用貪婪算法對接收信號y和感知矩陣T采用迭代優化的策略求解式(6)欠定最優化問題，從而求解得到稀疏信道。

互聯網讓資訊變得更便利，新媒體時代的到來帶來了海量的創新創業相關信息，足不出戶便能縱觀天下。通過對大數據的分析，可以了解市場供需、用戶需求、消費習慣、心理偏好等，敏銳的找到突破口。比如“餓了么”“美團”“滴滴”等新應用就是為滿足市場需求而量身打造適合當代人用戶體驗的成功案例，這些平臺一經推出，受到一致好評和廣泛應用。師范生可結合專業特點，借助網聯網+，尋找師范類成功范例。相應地，我們在獲取數據的同時也在貢獻數據，崇尚個性的年代大家習慣性的將自己衣、食、住、行和小創意分享在社交網站上，這也給師范生創新創業提供了新的啟發和更大的可能。

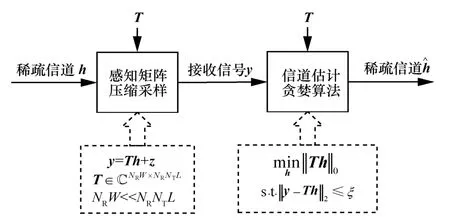
圖2 基于傳統貪婪算法的壓縮感知信道估計算法原理

4 基于深度學習的壓縮感知稀疏信道估計

針對FDD 大規模MIMO 下行鏈路的稀疏信道估計技術研究，上述傳統貪婪算法的壓縮感知信道估計算法通過迭代優化的策略求解CS 模型中的欠定最優化問題。這種迭代優化的密集計算以及不能保證全局最優的問題已成為CS 在大規模MIMO 系統稀疏信道估計應用中的瓶頸。為了進一步提高信道估計的精度和運算速度，以解決CS 算法在大規模MIMO 系統實時場景的應用中運算速率慢的問題，本文進一步提出了一種基于深度學習的壓縮感知ConCSNet 稀疏信道估計算法。

基于深度學習的壓縮感知信道估計算法原理如圖3 所示。首先，通過感知矩陣T對稀疏信道h進行壓縮采樣；然后，利用深度學習的方法對接收信號y采用端到端的學習優化策略求解式(6)欠定最優化問題從而求解得到稀疏信道。這2 個步驟分別對應于壓縮感知理論中的壓縮采樣和稀疏重構過程。然而，與傳統的基于貪婪算法的CS 信道估計算法相比，本文提出的基于深度學習的壓縮感知稀疏信道估計算法有根本的區別：1) 本文所提出的算法在求解過程中不需要知道信道稀疏度的先驗知識和感知矩陣T，這樣能進一步拓展該算法在信道估計領域中的應用范圍；2) 求解式(6)欠定最優化問題采用端到端的方式，而不是迭代優化的方式，這樣能極大地提高大規模矩陣運算的求解速度。本文將進一步對所提基于深度學習的壓縮感知ConCSNet 稀疏信道重構算法進行詳細說明。

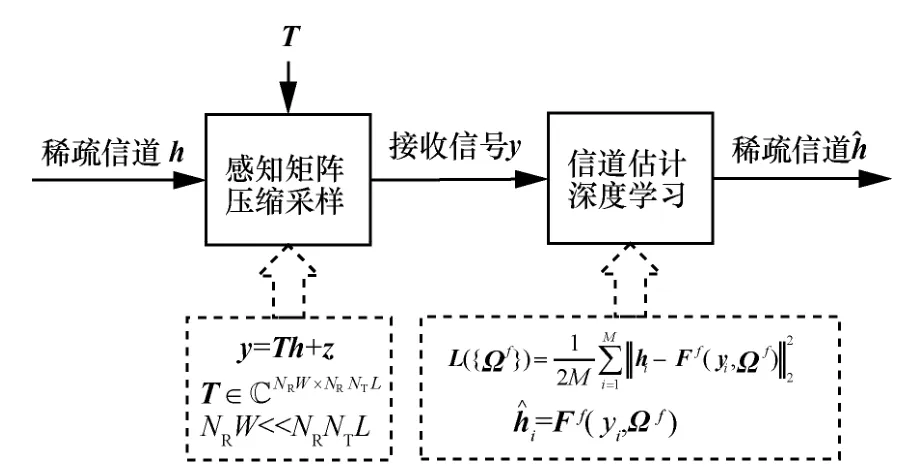
圖3 基于深度學習的壓縮感知信道估計算法原理

本文所提ConCSNet 結構如圖4 所示。該算法首先通過感知矩陣T對稀疏信道h進行壓縮采樣得到接收信號y，然后使用一個全連接層的線性映射網絡得到信道的近似解，最后由多層的卷積神經網絡得到更高質量的重構信道。值得注意的是，由于接收信號y和信道信息h均為復數，并且神經網絡通常以實數作為輸入，因此需要對數據進行預處理，這里分別對訓練數據以及標簽的實部和虛部進行拼接。為了盡可能地保留復數信號y的信息和提高信道估計的精度，在ConCSNet 算法的輸入端，將復數轉化為輸入矩陣，其中，yR為y的實部，yI為y的虛部，為y的能量值。而標簽轉化為一個三維NRNT×L×2的矩陣，該矩陣的第三個維度用來刻畫數據的實部和虛部。在ReconNet（reconstruction network）深度學習重構框架[16]中，卷積層只有6 層，且所使用的卷積核過大，不但增加了計算的復雜度，而且重構的細節部分效果不佳。因此，該網絡不適用于更高精度需求的信道估計場景。而本文提出的ConCSNet 算法一方面增加了卷積層的層數，擴展了卷積神經網絡的規模；另一方面縮小了部分較大的卷積核，使該網絡更聚焦于重構細節。接下來，本文將對ConCSNet 所包含的線性映射網絡和卷積學習網絡分別進行介紹。

圖4 ConCSNet 結構

4.1 線性映射網絡

對于式(5)，從測量信號y重構出原始信道信息h，該步驟可近似看作一個線性映射的過程，即h=Ωy，其中，為線性映射矩陣。由于，該映射過程求解的是一個欠定最優化問題，難以求出精確解。在基于貪婪算法的CS 信道估計算法中，通常利用感知矩陣T的偽逆和接收信號y的乘積求出初始的重構信道，然后通過迭代的方式逐步優化得到精確的稀疏信道。因此，與貪婪算法類似，本文采用線性映射網絡Ff求得初始的重構信道。線性映射過程得到的信道信息為近似解，其對應的線性映射矩陣為Ωf，并使的誤差最小。假設訓練集中包含M個訓練樣本，即。其中，為接收信號的測量值，為時域頻率選擇性衰落信道信息矩陣。對于該全連接層線性映射網絡，其損失函數可以表達為

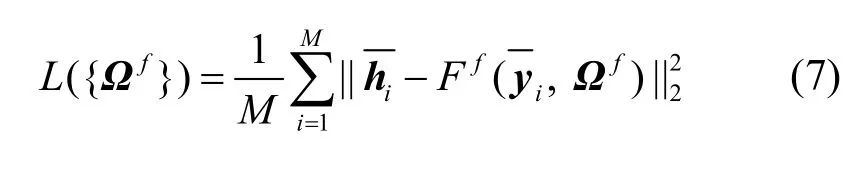
其中，Ff(·) 表示線性映射，訓練過程使用Adam方法進行訓練。則該網絡得到的信道h的近似解為

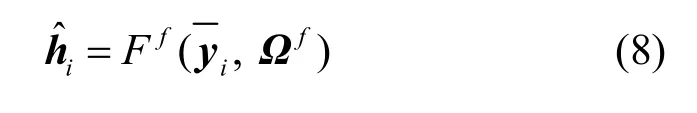
4.2 卷積學習網絡

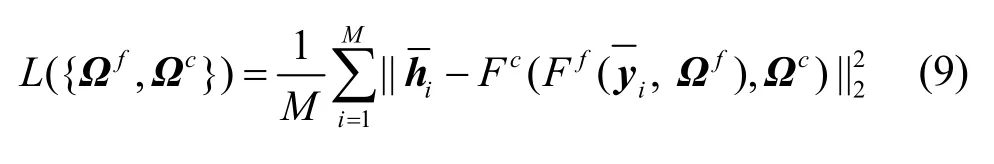
則該網絡得到的信道h的精確解為

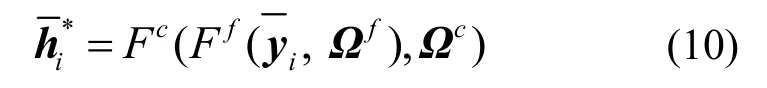
5 仿真與實驗結果分析

針對FDD 大規模MIMO 下行鏈路系統，本文將進一步驗證所提出的基于深度學習的壓縮感知稀疏信道估計ConCSNet 算法的性能。該仿真系統發射端和接收端的天線數分別為16 和4，OFDM 總子載波數為1 024；每一徑頻率選擇性衰落信道的長度和稀疏度分別為128 和9；導頻數為64，并且所有導頻都以塊狀的方式隨機放置。本文采用LTE-Advanced 信道模型[17]，主要包含3 種應用場景：擴展行人（EPA,extended pedestrian A）、擴展車輛（EVA,extended vehicular A）和擴展典型城市（ETU,extended typical urban）模型。本文中主要考慮EVA無線通信環境，其主要參數如表1 所示。

表1 大規模MIMO 系統參數

5.1 評估標準

為了進一步客觀評估所提出ConCSNet 深度學習信道估計算法和其他重構算法的性能，本文采用均方誤差（MSE,mean square error）和峰值信噪比（PSNR,peak signal-to-noise ratio）作為評價指標進行分析。

MSE 用來衡量重構值與真實值之間的差距。MSE 越小，說明重構性能越好。MSE 的表達式為

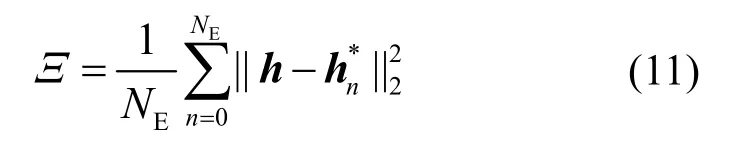
其中，NE為仿真次數，本文取值為20。

PSNR 提供了一個衡量信號失真或是噪聲水平的客觀標準。通常PSNR 越大，則說明信號重構失真度越小。其定義為

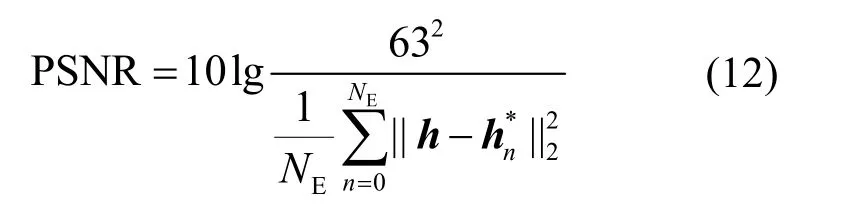
5.2 ConCSNet 訓練參數配置及細節

所提ConCSNet 的訓練過程包括以下2 個步驟。首先，訓練線性映射網絡Ff(·)，學習率為0.001，動量因子為0.95；Ff(·) 訓練完成后，對整個網絡進行訓練，此時改用較小的學習率0.000 1，也使用Adam 方法進行訓練，其動量因子為0.99。其次，采集204 800 個樣本作為總數據集，隨機打亂后，依次取128 000、38 400 和38 400 個樣本分別作為訓練集、驗證集和測試集。其中，訓練集用于模型訓練，驗證集用于估計模型的訓練水平，測試集用于評估模型最終的性能。批量大小是128，學習率衰減因子為0.96，學習率的衰減周期為100。本文使用Tensorflow 框架實現該網絡，并使用Intel Core i5-4200H CPU 在2.8 GHz 下對其進行訓練。

5.3 實驗結果

本節將所提ConCSNet 與已有算法進行比較，對比算法分別為LS[6]、Orale LS、OMP[9]、SAMP[11]、CoSaMP[14]、gOMP[15]和ReconNet[16]。其中，LS 為直接線性重構算法，Orale LS 為已知全部索引集的精確重構，OMP、SAMP、CoSaMP 和gOMP 算法為壓縮感知迭代重構算法，ReconNet 和ConCSNet為基于深度學習的重構算法。

在信噪比為0～30 dB 的條件下，LS、Orale LS、OMP、SAMP、CoSaMP、gOMP、ReconNet 和ConCSNet 的MSE 性能如圖5 所示。實驗結果表明，SAMP 在低信噪比下重構性能較差，而在較高信噪比下重構性能優于 CoSaMP。這是因為SAMP 閾值參數的確定直接與信道重構的精度相關，閾值參數設置太小則容易引入更多索引集，在后續的殘差比較過程中步長不斷擴大而無法準確估計稀疏度，導致在低信噪比下的重建過程中容易出現混亂，信道估計的精度較差。gOMP 隨著信噪比的增加逐漸逼近ReconNet 的重構性能。以深度學習為代表的ConCSNet 和ReconNet 重構算法，在各信噪比下的重構性能均優于基于傳統貪婪算法的CS 重構算法（OMP、SAMP、CoSaMP、gOMP）。當信噪比為15 dB 時，ReconNet 的MSE比gOMP 少2×10-4dB，而ConCSNet 的MSE 比gOMP 少4×10-4dB。這是因為基于深度學習的算法能夠很好地根據大規模的數據集學習到重構信號潛在的特征量，并通過非線性映射完成重構過程。所提ConCSNet 由于優化了網絡端輸入量的信息、采用初始線性映射網絡和進一步優化的卷積學習網絡進行信號重構，重構性能相比ReconNet 得到了進一步改善。

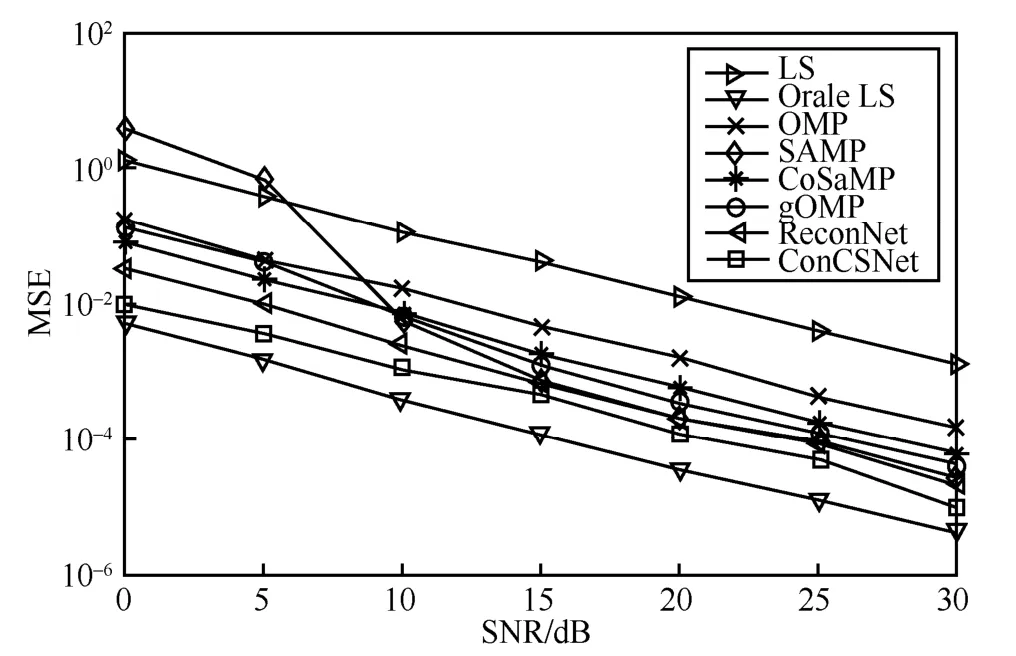
圖5 不同信噪比下，各算法的MSE 性能比較

圖6 和表2 分別給出了LS、Orale LS、OMP、SAMP、CoSaMP、gOMP、ReconNet 和ConCSNet算法在不同采樣率下的MSE 性能，其中信噪比為15 dB，并定義采樣率為導頻數與信道長度的比值。

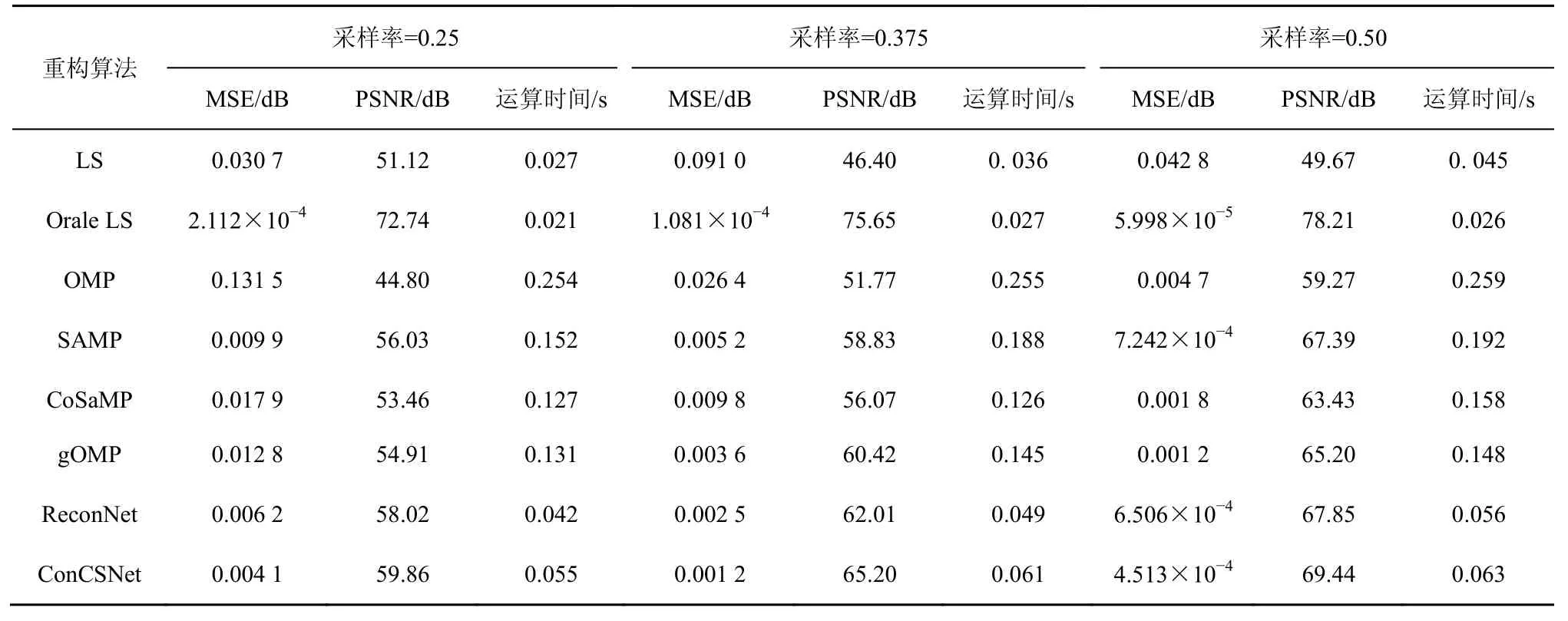
表2 不同采樣率時的性能對比

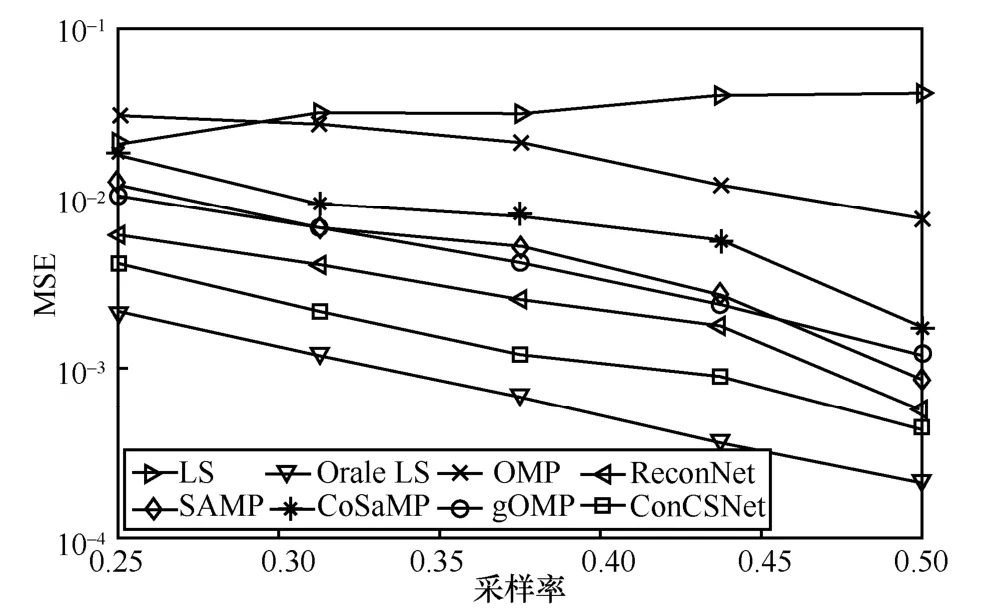
圖6 不同采樣率下，不同算法的MSE 性能比較

實驗結果表明，采樣率的增加對各算法的重構性能都能得到改善。當采樣率為0.3 時，gOMP 的性能劣于SAMP。當采樣率為0.375 時，ReconNet的MSE 比gOMP 少1.1×10-3dB，ConCSNet 的MSE 比ReconNet 少0.001 3 dB，而PSNR 性能領先3.19 dB。進一步地，當采樣率為0.25～0.5 時，基于傳統貪婪算法的壓縮感知重構算法（SAMP、CoSaMP 等）的信道估計性能不穩定。這是因為此類貪婪算法是根據殘差向量與感知矩陣之間相關性較大的一些分量，逐步找到原始信號的支撐集，并進一步重構原始信號。因此此類算法的特點是在滿足RIP 時，可以對原始信號以一定的概率進行重構。當采樣率取不同值時，則會影響重構的概率，因而出現波動和不穩定的現象。而基于深度學習的重構算法ConCSNet和ReconNet均能保持較好的性能，且ConCSNet 優于ReconNet。

圖7 分別展示了LS、Orale LS、OMP、SAMP、CoSaMP、gOMP、ReconNet 和ConCSNet 在不同稀疏度下的MSE 性能，其中信噪比為10 dB，采樣率為0.5。實驗結果表明，當稀疏度大于6 時，SAMP的性能逐漸優于CoSaMP。在相同的稀疏比下，由于利用了信道稀疏性，基于CS 的信道估計算法（OMP、SAMP、CoSaMP、gOMP、ReconNet 和ConCSNet）比傳統的線性算法LS 具有更好的性能，說明壓縮感知理論在稀疏信道估計的應用中不但能提高導頻的利用率，而且能夠進一步提高FDD大規模MIMO 信道估計的精度。當稀疏度為9 時，ReconNet 的MSE 比gOMP 少1.6×10-3dB，而ConCSNet 的MSE 比ReconNet 少0.000 8 dB。隨著稀疏度的增加，信道包含的信息也越豐富，各算法的重構性能逐漸變差。針對FDD 大規模MIMO 下行鏈路系統稀疏信道估計，本文提出的ConCSNet在不同的稀疏度下均能保持良好的重構性能，并優于ReconNet。

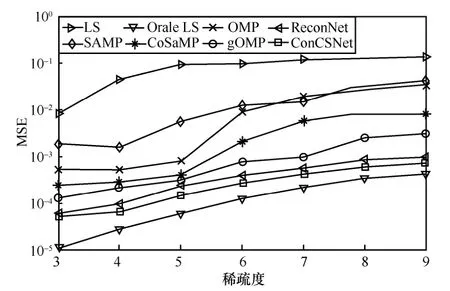
圖7 不同稀疏度下，不同算法的信道估計MSE 性能比較

表3 分別給出了LS、Orale LS、OMP、SAMP、CoSaMP、gOMP、ReconNet 和ConCSNet 在不同場景（EPA、EVA 和ETU）時的MSE 和PSNR 性能。在不同場景下，本文提出的ConCSNet 均優于其他算法，并且在ETU 場景下，ConCSNet 的MSE 性能優于ReconNet1.751×10-4dB，而PSNR 性能領先0.88 dB。由此可見，本文提出的基于深度學習的ConCSNet 適用于多場景環境。

此外，表2 和表3 均給出了在不同測試環境下的LS、Orale LS、OMP、SAMP、CoSaMP、gOMP、ReconNet 和ConCSNet 的運算時間，以反映各算法的時間復雜度。實驗結果表明，基于深度學習的ConCSNet 和ReconNet 相比于傳統迭代的CS 重構算法，其重構速度提高2～3 倍。由表2 可知，本文提出的ConCSNet 由于增加了卷積的層數，相比于ReconNet，重構時間多0.01～0.02 s。但是，相比于OMP 等算法，多花費的時間占比較小，且進一步提高了重構性能。因而，本文提出的ConCSNet綜合性能相比于其他算法仍然較優異，展現出較好的應用前景。

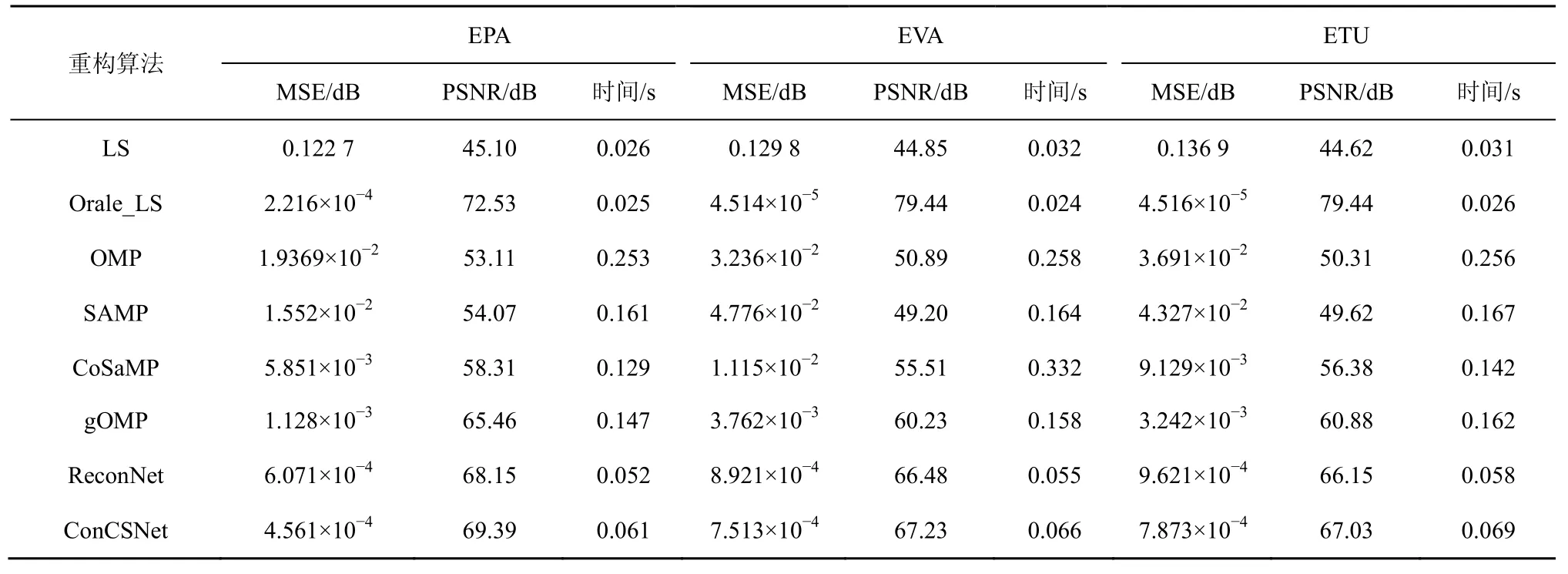
表3 不同場景時的性能對比

圖8 描述了LS、OMP、SAMP、CoSaMP、gOMP、ReconNet 和ConCSNet 在信噪比為0～30 dB 時的系統誤比特率性能。誤比特率是衡量信道估計算法對系統整體性能影響的宏觀指標。仿真結果表明，隨著信噪比的增大，各算法的誤比特率性能下降，說明信噪比越高，信道重構誤比特率性能越好。當信噪比一致時，與其他算法相比，本文提出的ConCSNet 算法具有更好的性能。當信噪比為20 dB時，系統的誤比特率達到4.34×10-4。

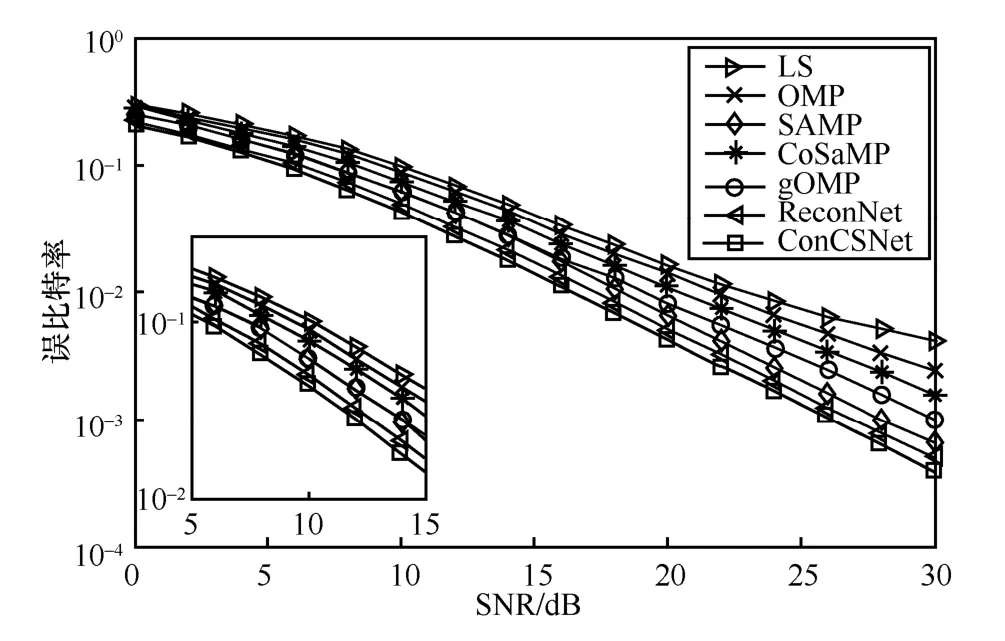
圖8 不同信噪比下，不同算法的信道估計誤比特率性能比較

6 結束語

針對FDD 大規模MIMO 下行鏈路系統模型，本文提出了一種新型的基于深度學習的壓縮感知稀疏信道估計算法ConCSNet。該算法在不需要稀疏度的情況下，通過數據驅動的方式，采用卷積神經網絡學習從測量向量y到信號h的逆變換，從而解決CS 框架下的欠定最優化問題，并實現對原始信道的重構。實驗結果表明，與傳統的基于 CS 的信道估計算法相比，本文提出的ConCSNet 的性能提升明顯，且重構速度能提高2～3 倍。該算法能夠解決傳統的基于迭代的CS大規模MIMO 信道估計算法計算時間長、重構效果不佳的問題。