基于LMD-SVD和極限學習機的滾動軸承故障診斷方法研究

劉 洋，孟祥川，許同樂

（山東理工大學機械工程學院，山東 淄博 255049）

1 引言

滾動軸承是高溫風機的重要部件，也是易損件。風機故障中與軸承損傷有關的幾乎占到了三成[1、2]，因此對風機軸承故障診斷是非常有必要的。傳統的滾動軸承診斷方法主要是快速傅里葉變換，然而在非平穩、非線性工況下故障信號效果不佳。針對振動信號為非線性、非平穩信號的情形，國內外學者提出一些常用的時頻分析方法，例如小波包變換（WPT）、經驗模式分解（EMD）、HHT[3-5]。WPT具有在時頻域提供局部特征和識別振動信號突變分量的特性，但WPT本質上是一個可調窗口傅立葉變換，并非每個分解分量的所有瞬時頻率都具有物理意義，WPT計算時間冗長，當數據量較大時難以實現；EMD是一種自適應信號處理方法，可以將信號分解為一系列正交分量，成為本征模函數，再基于本征模函數進行希爾伯特變換，得到信號的全能量-頻率-時間分布；HHT是EMD與希爾伯特變換的結合，由于EMD與HHT均有自適應分解的特點，在機械故障檢測領域得到廣泛應用。但是，EMD存在過度包絡、模式混淆等缺陷，且HHT獲得的負頻率可解釋性差。局部均值分解（LMD）是由Smith于2005年提出的，LMD適于將非線性和非平穩振動信號自適應分解為一系列乘積函數，每個乘積函數是包絡信號和具有物理意義的瞬時頻率的純調頻信號的乘積。LMD形式上與EMD相似，但已證明LMD在某些方面優于EMD，如信號更好的局部特征和時間尺度以及抵抗過沖影響的能力，并且需要更少的解碼組件。

將采用LMD方法從復雜滾動軸承振動信號里提取出變工況下的故障特征，但是基于LMD得到的PF分量對于分類方法的輸入而言過大，為解決這一問題，引入奇異值分解（SVD）來壓縮故障特征向量的尺度，從而提高特征向量的魯棒性。極限學習機（ELM）是一種機器學習算法，在大量回歸分析中得到應用，相比支持向量機（SVM）需要更少的人為干預，運行時間也更少，分類精度也更高。將采用ELM方法對滾動軸承進行不同工況下的故障狀態分類。

2算法分析

2.1 LMD算法

LMD算法在局部均值計算、分解分量、瞬時頻率計算等方面具有一定的優越性，且沒有嚴重的端點效應。為了從振動信號中提取故障信息，LMD算法可以將原始信號分解為一系列單分量調頻調幅信號（PF），PF的物理意義是包絡信號與調頻信號的乘積，進而可以導出瞬時頻率，LMD是通過逐步滑移信號實現的[6-8]。通過分解過程，原始信號可以根據下式重構：

原始信號x(t)可以由所有的PF和單調函數uk進行重構，說明LMD可以保證原始信號的完整性，進而可以提取出完整的故障信息[9、10]。并且LMD得到的分解分量少，這一優勢可以保證特征信息不會被分割成多個相鄰的分解層[11]。但是基于LMD得到的PF分量對于分類方法的輸入而言太大了，為了解決這一問題，本研究引入奇異值分解（SVD）來壓縮分解分量的尺度。

2.2 SVD理論

SVD是基于相空間重構的降噪方法，通過對一維時間序列實現Takens相空間重構，得到重構維數p和延遲步長q。再對重構以后的矩陣實現奇異值分解，從而基于噪聲和信號的能量可分性，達到降噪目的。奇異值是矩陣的固有特征，穩定性好，即便矩陣中某個元素發生改變，矩陣奇異值變動很小，同時矩陣奇異值還具備比例不變與旋轉不變性質。總而言之，矩陣奇異值滿足模式識別的特征要求。

設原始信號采樣點數量為n，真實PF分量的個數等于m，那么可以得到m×n的矩陣X，X的SVD如下式：

式中：U、V—m階與n階的正交方陣；S—m×n階的斜對角矩陣，其中，σ=diag(σ1，σ2，σ3，...，σr)），σi—矩陣的奇異值，且均不小于0。

從上式可以看出，X可以看作特征向量ui，vT i作外積以后與奇異值的加權和，權重是非零奇異值。權重越大，則特征向量在重建信號中所占比例越大。

基于LMD-SVD特征提取的主要流程如下：

（1）對信號x*(t)實現LMD分解，獲得頻率由高而低的若干PFi(i=1，2，...，n)分量；

（2）通過相關系數與方差貢獻率得到起主導作用的PF分量，并構成特征矩陣X；

（3）對特征矩陣X進行SVD分解，獲得相應奇異值，即為滾動軸承信號的特征向量。

2.3極限學習機

文獻[12]最初提出的極限學習機（Extreme Learning Machine，ELM）是針對單隱層前饋神經網絡開發的，然后擴展到“廣義”單隱層前饋網絡（SLFN）。ELM是一種新的學習算法，具有更快的學習速度和更好的泛化性能[13]。SLFN結構，如圖1所示。

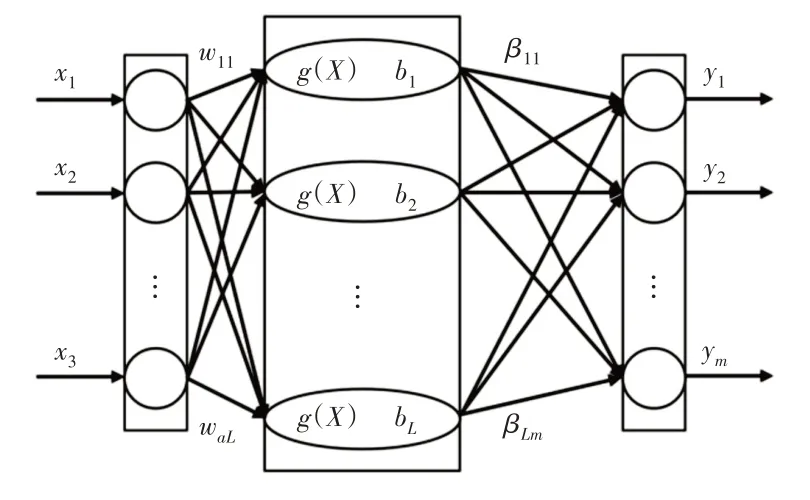
圖1單隱層前饋網絡結構Fig.1 Single Hidden Layer Feedforward Network Structure

圖中：Xi—輸入樣本—輸入層中所有節點之間的鏈路權重向量；g(x)—隱藏層中神經元的激活函數；bi—閾值。隱藏層中的神經元隱藏層中的第i個節點和輸出層中的所有節點之間的鏈路權重向量；yi—網絡的輸出；n—輸入層中的節點數量；L—隱含層中的節點數量；m—輸出層中的節點數，j=1，2，…，n。

ELM的數學模型如下描述：

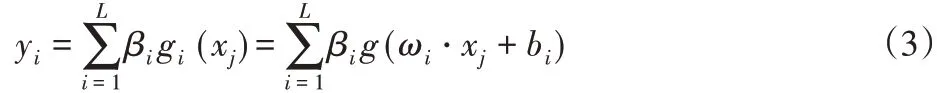
ELM對激活函數g(x)不敏感，而且幾乎所有滿足ELM泛逼近能力定理的非線性分段連續函數都可以作為激活函數[14]。例如：

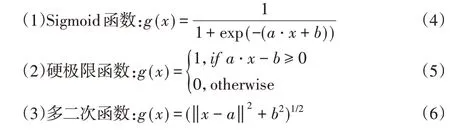
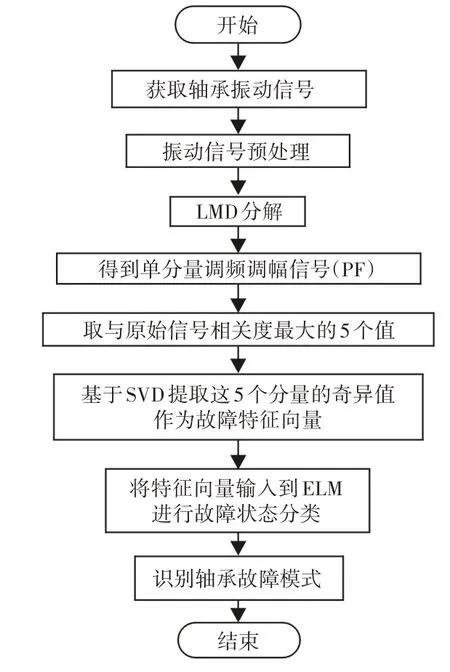
圖2基于LMD-SVD和極限學習機的滾動軸承故障診斷方法流程Fig.2 Fault Diagnosis Process of Rolling Bearing based on LMD-SVD and Extreme Learning Machine

Sigmoid函數是前饋神經網絡中的主要激活函數，具有硬極限函數和多二次函數的ELM也具有良好的性能。在研究中，選擇Sigmoid函數作為激活函數。ELM算法流程如下：（1）確定隱層神經元數目L和激活函數g(x)，隨機分配i、b i和βi；（2）計算隱層輸出向量；（3）計算輸出權重β?。

3 基于LMD-SVD和極限學習機的滾動軸承故障診斷方法

軸承故障診斷總流程圖，如圖2所示。

3.1 實驗數據采集

本研究實驗采用的軸承實驗系統由功率為1470W的電動機、試驗軸承、扭矩傳感器和電氣控制裝置組成，軸承轉速為1750r∕min。數據采集卡采用NIPCI-4472，采樣頻率設定在12000Hz。加速度傳感器安裝在電動機的驅動端以獲取軸承的振動信號，軸承尺寸內徑25mm、外徑52mm、寬度15mm。故障的引入采用電火花加工方法。試驗滾動軸承為SKF公司的6205-RS深溝球軸承。試驗臺由2馬力電機、液力變矩器∕編碼器、測功機和控制電路組成。采用安裝在磁基殼上的加速器傳感器，采集正常、內圈故障、外圈故障和滾動體故障等振動信號。針對各種故障模式在不同運行條件下各采樣25組數據，總共獲得400組數據。滾動軸承故障診斷臺的結構圖及實物圖分別，如圖3、圖4所示。

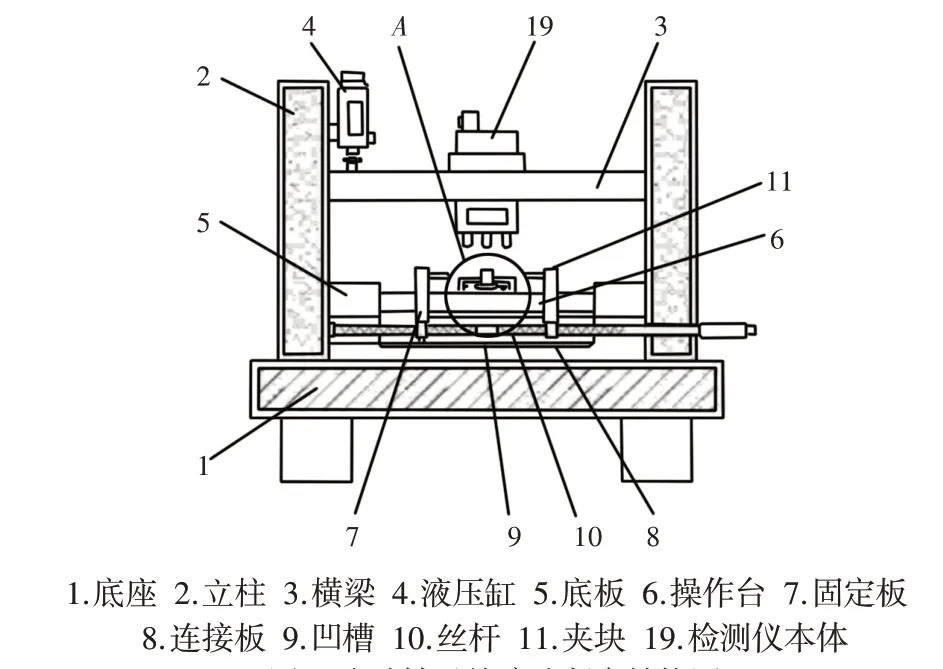
圖3 滾動軸承故障診斷臺結構圖Fig.3 Structure Drawing of Rolling Bearing Fault Diagnosis Table

圖4 滾動軸承故障診斷臺實物圖Fig.4 Physical Drawing of Rolling Bearing Fault Diagnosis Table

3.2 基于LMD-SVD特征提取

為了獲取故障特征向量，首先應用LMD將原始振動信號分解成多個PF，如圖5所示。得到的PF即為原始信號的調頻調幅信號，信號包絡線為對稱的，是一系列具有物理意義的瞬時頻率PF分量之和。由LMD-SVD獲得的故障特征值部分，如表1所示。從表中可以看出，經過分解后的分量最終可由故障特征向量表示，每個故障特征向量均包括五個數據。

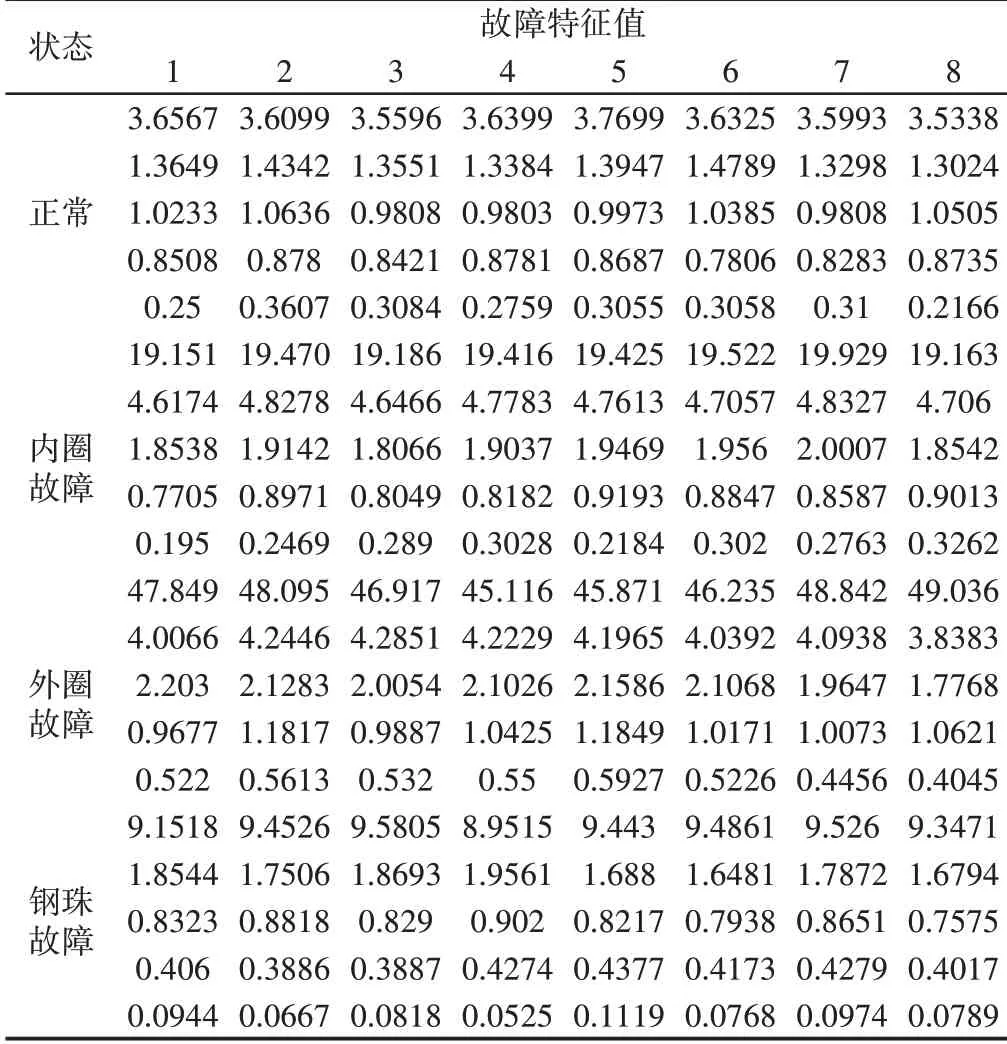
表1 基于LMD-SVD得到的故障特征值Tab.1 Fault Eigenvalues Obtained based on LMD-SVD

圖5 基于LMD獲得的振動信號PFFig.5 Vibration Signal PF Obtained based on LMD

將基于LMD-SVD所得到的不同狀態下的8組故障特征值（奇異值）繪制在同一坐標系下，即得到內圈、外圈和滾動體故障的奇異簇，如圖6所示。

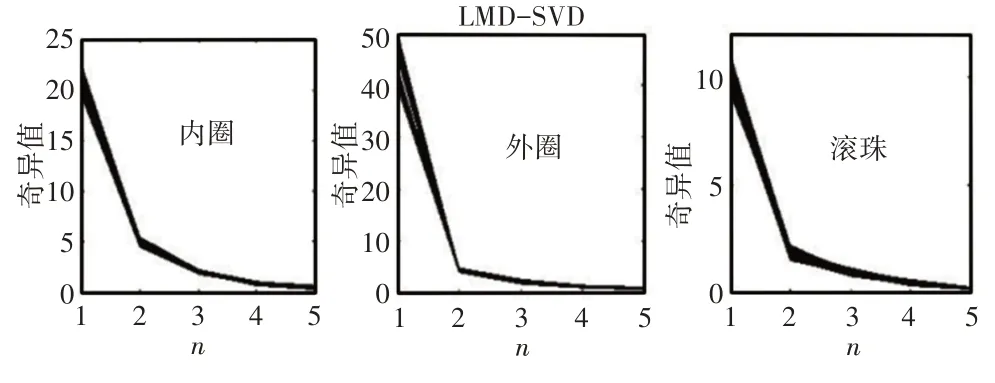
圖6 內圈故障信號、外圈故障信號和滾動體故障信號奇異值聚類Fig.6 Singular Value Clustering of Inner Ring Fault Signal，Outer Ring Fault Signal and Rolling Body Fault Signal

顯然，對于一個特定的故障模式，LMD-SVD得到的奇異值線在不同的運行條件下幾乎是一致的。也就是說，奇異值向量即使在變化的條件下也保持高度的一致性。因此，在可變條件下的特征提取方面，LMD-SVD具有顯著優勢。這些特性保證了在可變條件下應用所提出的特征提取方法的有效性。

在本研究中，滾動軸承的運行狀態包括正常、內圈故障、外圈故障和滾動體故障。為了觀察不同工作狀態下奇異值的可分離性，由LMD-SVD得到的不同工作狀態下的奇異值簇，如圖7所示。從中我們可以看出，四個工作狀態之間的間隙足夠大，可以容易地將它們分開。由于奇異值在可變條件下保持了良好的可分離性，因此它們比較適合用作分類器的輸入。

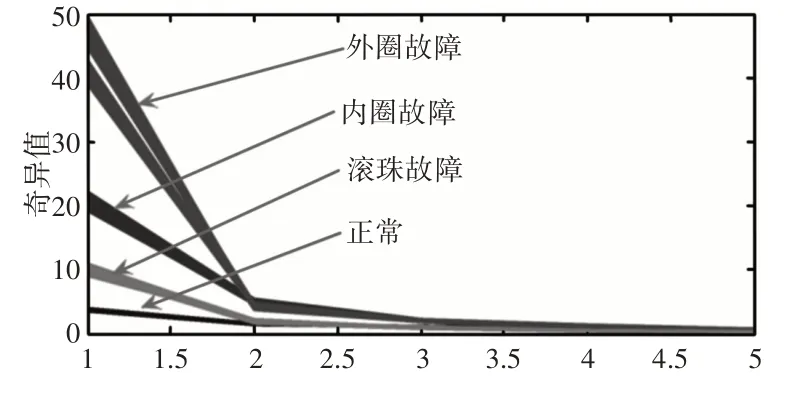
圖7 不同工作狀態下的奇異值聚類Fig.7 Singular Value Clustering under Different Working Conditions

由于本次使用的實驗數據來自實驗室裝置，因此振動信號的噪聲水平相對較低，為了驗證提出LMD-SVD方法在實際工程中應用的魯棒性，同時考慮到絕大多數工業應用都可能涉及加性噪聲，因此我們進行了LMD-SVD方法能夠抵御加性噪聲的實驗驗證。將信噪比分別為0.2、0.4、0.6和0.8的高斯白噪聲分別加入到原始振動信號中，將特征提取結果顯示，如圖8所示。由此可以看出，當信噪比從0.2變化到0.8時，所提取的特征是：當信噪比為0.2時，不同故障狀態之間的可分性良好。由于LMD能夠自適應地分解任何復雜多分量信號，因此得到期望結果。由于特征在變化條件下具有良好的可分離性，使得分類器易于進行故障診斷，從而得出LMD-SVD方法在一定程度上能夠抵抗噪聲的結論。

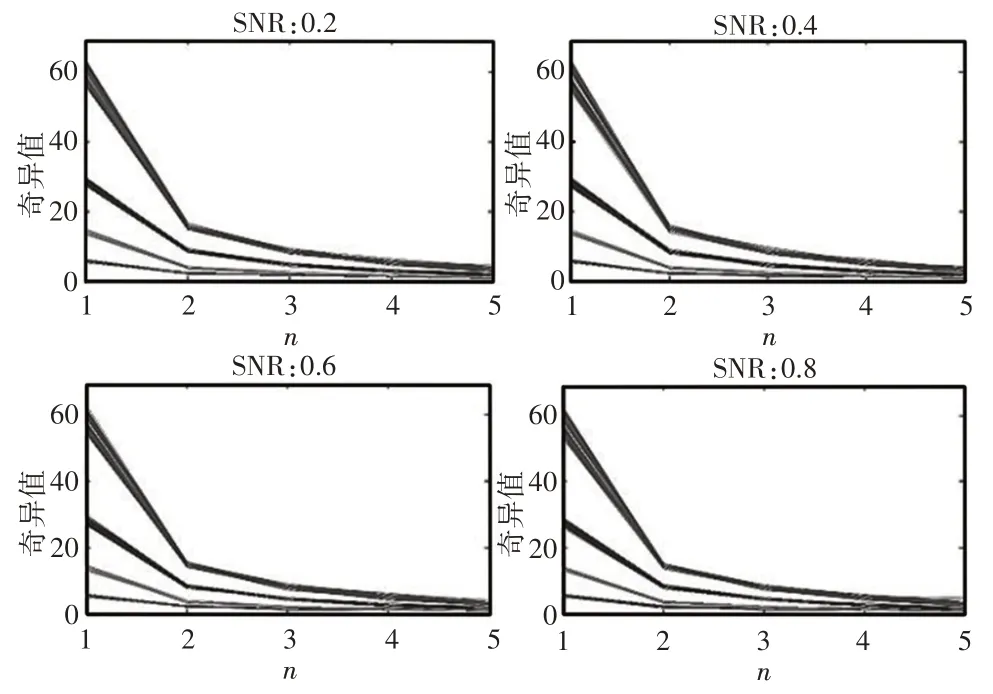
圖8 噪聲信號的LMD-SVD結果Fig.8 LMD-SVD Results of Noise Signal

3.3 基于極限學習機的故障狀態分類

基于LMD-SVD得到的故障特征向量可以用于滾動軸承工作狀態識別，而基于ELM的故障狀態分類結果部分，如表2所示。即使在可變的條件下，ELM的實際輸出也與目標輸出極其一致。因此，將LMD-SVD與ELM相結合可以有效地實現變工況下滾動軸承的故障診斷。

表2 基于ELM的狀態分類結果Tab.2 State Classification Results based on ELM

由于ELM與SVM相似，因此將ELM與SVM進行對比。顯然，ELM比SVM需要更少的人工干預，因為在ELM方法中，只有隱藏層中的神經元數量需要人工確定，而SVM中有兩個參數需要在訓練之前確定。SVM雖然提供了許多算法來調整兩個參數，但是如何選擇合適的算法是一個難題，因為它會對整個分類過程產生巨大的影響，特別是在運行時間和分類精度方面。同時，為了比較分類效果，將BP神經網絡的一個典型例子應用于分類中。因此，在我們的研究中，比較了ELM、SVM[15]和BP[16]在運行時間和分類精度方面的差異。由于訓練樣本的數量是分類中的重要影響因素，因此每個操作條件的訓練樣本數量被設置為10，每個操作狀態總共有40個樣本。詳細的比較結果，如表3所示。其中給出10個例子來計算運行時間和分類精度的平均值以進行比較。

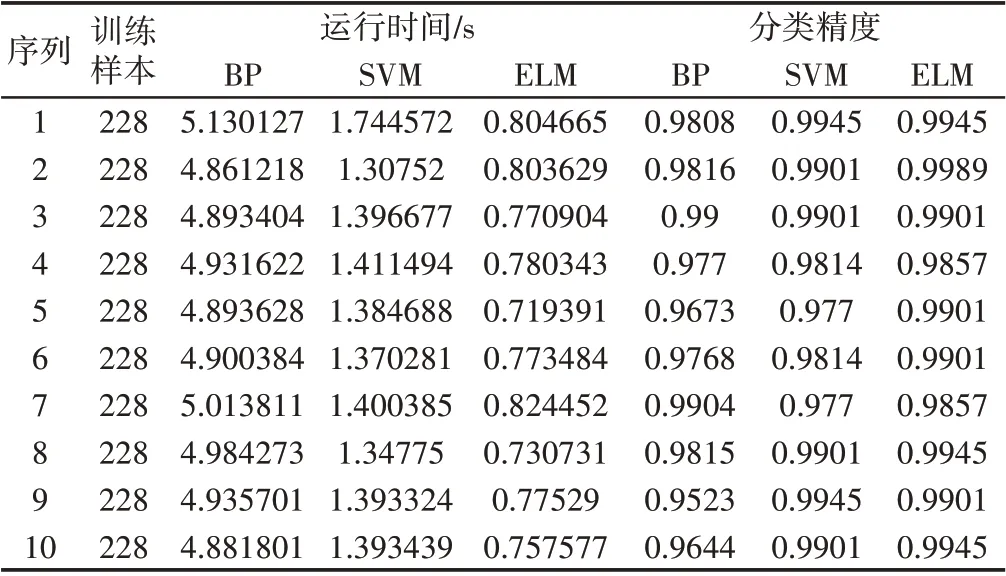
表3 ELM、SVM與BP的分類結果Tab.3 Classification Results of ELM，SVM and BP

BP方法明顯比另外兩種方法更耗時和更不精確，而且ELM在運行時間和分類精度方面相比SVM仍然具有優勢，如圖9所示。然而，由于故障特征向量具有良好的可分離性，ELM和SVM之間的差距不是很大，三種方法的分類精度都高于0.9，這進一步驗證了所提出方法的有效性。

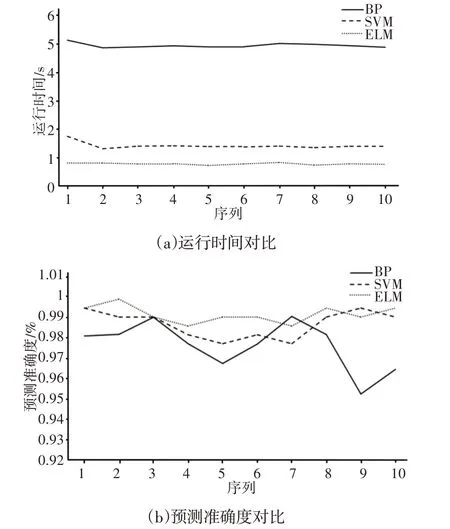
圖9 ELM、SVM和BP在運行時間和分類精度上的比較情況Fig.9 Comparison of ELM，SVM and BP in Terms of Running Time and Classification Accuracy

4 結論

提出了一種基于LMD-SVD和ELM的滾動軸承故障診斷方法，主要貢獻如下：（1）采用LMD-SVD方法提取故障特征向量，采用ELM方法對滾動軸承在變工況下的狀態進行分類；（2）在滾動軸承特征提取方面，對LMD-SVD方法進行了分析，表明LMD-SVD的優越性在于即使在變化條件下特征向量仍保持較高的重合度；（3）從運行時間和分類精度兩方面考慮，將ELM和SVM、BP算法作為故障分類的有效方法進行比較，發現ELM算法耗時少，精度高。

實驗結果表明，提出的LMD-SVD和ELM方法適用于變工況下滾動軸承的故障診斷，具有廣闊的應用前景。在本研究中，我們僅將此方法應用于滾動軸承，因此今后應在其他旋轉機械上進行實驗，以驗證此方法的通用性或發現推廣中存在的問題。