可變周期被動式減搖水艙設計與仿真研究

梁利華，王繼銘，宋吉廣，李陽

哈爾濱工程大學 智能科學與工程學院，黑龍江 哈爾濱 150001

0 引 言

船舶在海上受海浪影響所產生的各種搖晃運動一直以來備受關注。船舶的橫搖阻尼較小，導致其在六自由度的搖蕩運動中其橫搖運動幅值通常較大。因此，為了減小船舶的橫搖運動，保證船舶的穩定航行，研究人員設計了各種減搖裝置，其中常用的有減搖鰭和減搖水艙。作為目前應用最為廣泛的主動式減搖設備，減搖鰭可以在中、高航速下獲得良好的減搖效果，并且隨著現今技術的發展，還可以提供全航速范圍內的減搖作用。然而，減搖鰭也存在缺點，即其不僅造價較高，且運行能量消耗也較大[1]。

與減搖鰭相比，減搖水艙具有安裝成本低、運行能耗小等優點[2]。通常，減搖水艙按照控制方式可以分為被動式減搖水艙、主動式減搖水艙和可控被動式減搖水艙3 種。其中，被動式減搖水艙主要是根據船舶與減搖水艙之間的共振現象設計，即當水艙內水的固有頻率與船舶固有頻率相近時，水艙能達到良好的減搖效果； 主動式減搖水艙是根據具體船舶的橫搖運動情況，通過控制系統來主動改變減搖水艙內水的流動方向，從而達到減搖的目的；可控被動式減搖水艙則是通過控制安裝在水艙的氣閥或擋板來拓寬水艙的減搖頻帶，從而使其適應船舶不同的工作狀態，一般可以分為氣閥式可控被動水艙和可變周期被動式減搖水艙2 種[3]。

目前，在被動式減搖水艙研究方面已獲得很大進展。趙戰華等[4]研究了平面式減搖水艙水位變化對減搖效果的影響，表明艙內水位在水艙總高度50%～60% 范圍內時減搖效率最高。Rahul等[5]針對U 型減搖水艙提出了一種基于遺傳算法（GA）的優化方案，實驗表明，與未優化的水艙相比，優化后的減搖水艙可以將峰值橫搖響應降低約82%。

與其他在海面上航行的船舶不同，半潛船除了需要在海平面上航行外，有時還會在半潛狀態下潛航運動，或在全潛狀態下裝載其他船舶或進行潛艇救援。但是，若是半潛船裝載了其他船舶時會導致該船的橫搖周期變化范圍較大，同時，其還具有重心高、穩性差以及恢復力矩小等特點[6]，若半潛船處于長距離海上航行過程時，若遇大風浪侵襲，其會比其他類型的船舶更易發生大角度的橫搖運動，而過大的橫搖運動又會給其海上航行性能以及船上人員與貨物的安全性能帶來很大影響，因此這類船舶通常配備有減搖裝置。然而，由于半潛船會處于不同的工作狀態，其橫搖周期的變化范圍較大，所以可以采用可控被動式或主動式減搖水艙來進行減搖。但是，主動式減搖水艙在對水艙的控制上存在一定的困難，同時還會消耗大量的能量，經濟上很不合算[7]。鑒此，本文將針對半潛船設計可變周期被動式減搖水艙，通過控制水艙內擋板的使用數量來調整水艙的固有周期，以使其與不同工作狀態下船舶的周期都相匹配，從而達到減搖效果良好的目的。

首先，針對半潛船的周期變化特點初步設計減搖水艙的擋板結構；然后，通過計算流體力學(CFD)中的Fluent 軟件仿真計算不同數量T 型擋板結構對水艙固有周期的影響，進而根據半潛船3 種工作狀態的固有周期優化水艙的結構設計，以便在3 種狀態下均能實現較好的周期匹配；最后，基于自回歸(auto-regressive，AR) 模型預測船舶的下一個橫搖周期，根據預測的橫搖周期及時調整水艙擋板數量，改變水艙的周期。

1 船-水艙橫搖模型

1.1 船-被動式減搖水艙

可變周期被動式減搖水艙（或稱“可控被動式減搖水艙”）在本質上相當于由多個不同固有周期的被動式減搖水艙組合而成。本文研究的可變周期被動式減搖水艙是在U 型被動式減搖水艙的基礎上建立的，其取船體固定坐標系的原點o在船體重心位置，ox軸 指向船艏，oy軸指向右舷，oz軸指向船舶基線。因此，根據克雷洛夫-勃拉哥維新斯基(Krylov-Blagoveshchensk) 理論，即可得到船舶與U 型被動式減搖水艙的橫搖運動方程[8]。

船舶橫搖運動方程：

水艙內液體的運動方程：

1.2 水艙周期的調節原理

當船舶在海上航行時，會因受到海浪的影響而發生橫搖運動。此時，船舶的橫搖運動會滯后于海浪運動90°，同時，減搖水艙還會因其內部流體的慣性作用而使得艙內水的運動滯后于船舶的橫搖運動90°。因此，為了獲得較好的減搖效果，在設計減搖水艙時，減搖水艙的固有周期應等于或接近于船舶的固有周期。

雖然通過改變減搖水艙的尺寸大小在一定程度上能夠改變其固有周期，但是安裝在船舶上的水艙尺寸是固定的，如果沒有其他控制方法，水艙的固有周期也會固定不變。因此，水艙的固有周期是在進行減搖水艙結構設計時需要考慮的一個重要參數。可變周期被動式減搖水艙的周期Tφ可通過下面的公式近似計算：

由式（3）和式（4）可以看出，水艙固有周期的大小主要取決于水艙的邊艙寬度和水艙底部連通道寬度這2 個方面。

本文研究的可變周期被動式減搖水艙主要是通過控制水艙連通道內擋板的高度，來調整T 型擋板的使用數量。擋板數量的調整改變了連通道內水流動截面的寬度，相當于改變了水艙底部連通道內水的流量，進而可在一定程度上調整水艙的固有周期，使其在船舶的不同工況下都能達到良好的減搖效果。

2 可變周期水艙的結構設計

2.1 減搖水艙的初步設計

根據半潛船的結構尺寸，初步設計了可變周期U 型被動式減搖水艙的內部結構和外部結構，整體結構如圖1 所示。水艙內部結構最多可以有8 個擋板同時升起。水艙的主要尺寸如表1所示。水艙連通道內部的擋板結構為T 型擋板結構[11]。

圖1 減搖水艙的結構Fig. 1 Structure of anti-rolling tank

表1 水艙的主要尺寸Table 1 Main parameters of tank

2.2 T 型擋板數量對水艙周期的影響

為了研究不同T 型擋板數量對水艙固有周期的影響，將水艙底部連通道內的T 型擋板數量分為了4 種情況，分別為具有1 對T 型擋板、具有2 對T 型擋板、具有3 對T 型擋板和具有4 對T 型擋板的減搖水艙。

水艙底部連通道內的T 型擋板以水艙底部連通道的中心對稱，呈上、下為一對的配置方式。當水艙內部4 對T 型擋板全部工作時，其擋板結構如圖2 所示。

圖2 連通道內T 型擋板的結構Fig. 2 T-shaped baffle structure in the connecting channel

為了確定擋板數量對水艙固有周期的影響，采用CFD 軟件中Fluent 仿真軟件模擬水艙的自由衰減，得到減搖水艙力矩曲線圖，進而計算水艙的固有周期[12]。

1） 減搖水艙的網格劃分。

在對水艙的自由衰減進行仿真分析前，需要先對減搖水艙的幾何模型進行網格劃分，以便于后續的模擬計算。在對水艙模型進行網格劃分時，由于水艙內的液體在2 個邊艙和4 對擋板的附近晃蕩劇烈，因此需要在這2 個邊艙和4 對擋板這兩部分進行網格加密[13]。以具有4 對T 型擋板結構的水艙為例，加密后最終生成的網格圖如圖3 所示。

圖3 具有4 對T 型擋板水艙的網格圖Fig. 3 Grid diagram of tank with four pairs of T-shaped baffle

2） 減搖水艙的自由衰減。

為了獲得減搖水艙的固有周期，利用Fluent軟件針對水艙的自由衰減進行了模擬仿真實驗。在仿真初始時刻，設置使水艙其中一邊艙的液位高于另一邊艙，以使減搖水艙在重力的作用下，其艙內流體通過底部連通道作往復的振蕩運動，從而得到水艙內流體在兩邊艙運動時產生的力矩隨時間變化的曲線圖，然后根據該曲線圖計算出水艙的固有周期。

使用Fluent 軟件進行仿真時的主要參數設置如下：選擇3D 瞬態Transient 模型；重力加速度g=-9.81 m/s2；選擇流體體積(VOF)法捕捉水艙的自由液面變化和Realizablek-ε 湍流模型，其中選擇空氣為第1 相，水為第2 相的兩相流模型。

仿真實驗以具有4 對T 型擋板數量的減搖水艙結構為例，初始設置水艙的自由液面高度為4 m，使水艙的左邊艙液位高于右邊艙，初始設置云圖如圖4 所示。由此，得到具有4 對T 型擋板減搖水艙內流體運動產生的力矩隨時間變化的自由衰減曲線如圖5 所示。

圖4 具有4 對T 型擋板水艙的初始設置云圖Fig. 4 Contours of initial setting of tank with four pairs of Tshaped baffle

圖5 具有4 對T 型擋板水艙的自由衰減曲線圖Fig. 5 Free attenuation curve of tank with four pairs of T-shaped baffle

3） 小結。

對其他3 種具有不同T 型擋板數量的水艙結構依次進行水艙的自由衰減仿真實驗后，可以得到其他3 種具有不同T 型擋板數量減搖水艙的自由衰減曲線，然后由水艙的自由衰減曲線，即可計算得到具有不同數量T 型擋板下水艙的固有周期，整理計算后的數據如表2 所示。

表2 具有不同T 型擋板數量的水艙固有周期Table 2 Tank harmonic period under different numbers of Tshaped baffle

從表2 中可以看出，成對交錯的T 型擋板結構能夠通過減小水艙內流體的流動寬度來增加艙內水流動路徑的復雜度，從而可在一定程度上延長水艙的固有周期。同時，從數據中還發現，針對該尺寸的U 型減搖水艙，每增加一對T 型擋板，減搖水艙的固有周期增加約4 s，表明具有T 型擋板結構的減搖水艙能夠適應橫搖周期變化較大的船舶。

2.3 減搖水艙的優化

由于半潛船有空載、半載和滿載3 種工況，為了使減搖水艙能夠更好地適應船舶不同的工況以達到良好的減搖效果，針對某半潛船的船型參數及3 種工況下半潛船自身的固有周期，調整減搖水艙外部尺寸大小和內部T 型擋板的使用數量及間距，對水艙內部和外部結構進行了優化[14]。

對優化后的減搖水艙進行自由衰減仿真實驗，依次得到適應船舶3 種工況時水艙的周期，整理后如表3 所示。由表3 中數據可以看出，優化后的水艙可以與船舶在3 種工況下都具有較好的周期匹配。優化后的減搖水艙的整體結構如圖6所示。圖7 所示為半潛船在半載工況下，水艙內部只有3 個擋板工作時的狀態圖。表4 為優化后水艙的主要尺寸。

表4 優化后水艙的主要尺寸Table 4 Main parameters of optimized tank

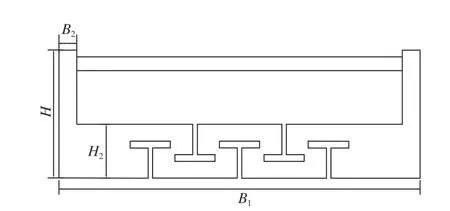
圖6 優化后的減搖水艙Fig. 6 Optimized anti-rolling tank

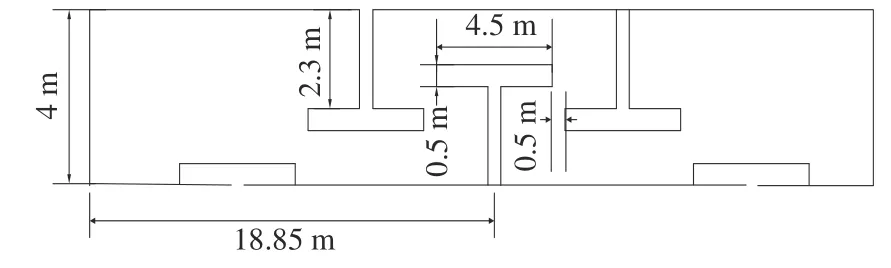
圖7 優化后的減搖水艙擋板結構Fig. 7 Optimized T-shaped baffle structure of tank

表3 3 種工況下船與水艙的固有周期Table 3 Ship and tank harmonic period under three working conditions

3 基于橫搖周期預報的擋板控制

隨機海浪可以認為是由不同幅值、頻率和初相位的余弦波疊加而成，船舶在海上航行時，船舶的橫搖周期是隨著海浪的浪向和船舶航速的變化而變化的。因此，當船舶與海浪的遭遇頻率發生變化時，其遭遇頻率可采用下述公式表示為

因此，船舶在隨機海浪干擾下的橫搖周期并不總是其3 種工況下的固有周期，而是會受到遭遇頻率的影響。為了使減搖水艙能夠獲得更好的減搖效果，需要根據船舶的橫搖周期及時調整水艙內T 型擋板的數量，以使減搖水艙與船舶橫搖達到最佳的周期匹配。

為了能夠在船舶的當前橫搖周期確定未來時刻（下一個船舶橫搖周期）T 型擋板的使用數量，以便在下一個橫搖周期實時控制T 型擋板的高度，需要知道未來時刻的船舶橫搖周期。這時，也就需要使用預報技術來對船舶的下一個橫搖周期進行預報。橫搖周期的預報屬于典型的時間序列預測問題，主要是從過去的數據中找出其變化的規律，然后使用這種變化的規律來對將來數據的變化作出預測[15-16]。常用的時間序列模型有：移動平均 (MA) 模型、自回歸(AR) 模型、自回歸移動平均(ARMA) 模型等。由于橫搖周期的預報比較簡單，所以本文使用了AR 模型。

系統的控制框圖如圖8 所示。通過慣性測量單元(IMU)，可以獲得船舶的橫搖角、角速度和角加速度，據此，即可以計算船舶的橫搖周期。AR周期預報單元用于存儲之前的周期值，以對下一個周期值進行預報，同時，根據預測的周期值T?k+1，通過查表的方式即可確定水艙中T 型擋板的配置，從而使水艙的周期最接近T?k+1。根據查表獲得的擋板配置可用于控制水艙中T 型擋板的高度。最終，水艙形成穩定力矩Mc用于對抗海浪的擾動力矩Mω。

圖8 控制系統原理框圖Fig. 8 Block diagram of control system

4 仿真分析

為了驗證第3 節所提的基于橫搖周期預報的擋板控制減搖水艙的減搖效果，以某型半潛船為例進行了仿真分析，其3 種工況下的主要船型參數如表5 所示。

表5 半潛船模型參數Table 5 Parameters of semi-submersible ship

通過Matlab 軟件搭建船-可變周期被動式減搖水艙數學模型，分別在規則波海浪和不規則波海浪這2 種情況下進行半潛船-可變周期被動式減搖水艙的仿真。圖9 和圖10 所示分別為仿真得到的船舶半載工況下規則波和不規則波時海浪波傾角與船舶橫搖角的曲線。

圖9 規則波下的海浪波傾角與船舶橫搖角（半載工況）Fig. 9 Wave slope and ship roll angle under regular waves (halfload draught)

圖10 不規則波下海浪波傾角與船舶橫搖角（半載工況）Fig. 10 Wave slope and ship roll angle under irregular waves(half-load draught)

本文的規則波以正弦函數 αe=4sinωt作為海浪波傾角的輸入形式。當ω=ωφ=ωt=0.50 rad/s（其中 ω為海浪的頻率， ωφ和 ωt分別為船舶與水艙的固有頻率）時，海浪、船舶和減搖水艙三者之間會發生諧振運動，此時，減搖水艙產生的減搖力矩完全用來抵抗海浪產生的環境擾動力矩，故此時的減搖效果最佳。

從圖9 中可以看出，在規則波海浪下無減搖水艙時，即減搖前船舶橫搖角為15.54°，增加了減搖水艙之后船舶的橫搖角為4.48°，此時，從相位關系來看，減搖水艙的液位變化滯后于船舶的橫搖運動90°，故此時減搖效果最佳且達到了71.18%。但是，由于規則波海浪是一種較為理想的海浪形式，一般很難真實反映海上海浪的運動狀態，同時，此時AR 模型對橫搖周期的預報非常準確，所以需要考慮實際工作中不規則波的情況。

不規則波以海浪有義波高4 m、海浪的遭遇角90°以及船舶航速14 kn 為條件進行仿真分析，結果如圖10 所示。

從圖10 中可以看出，在不規則波海浪下無減搖水艙時，即減搖前船舶的橫搖角為5.44°，增加了減搖水艙之后船舶的橫搖角為3.94°，此時，減搖效果達27.57%。減搖效果明顯降低主要有3 個方面的原因：1）未減搖時船舶的橫搖角變小，由15.54°降到了5.44°；2）在非規則波下，AR 模型對橫搖周期的預報存在一定的誤差；3）在圖9 所示規則波條件下，水艙周期和船舶橫搖周期基本相等，而在非規則波條件下只是比較接近。

圖11 所示為船舶空載工況下不規則波時海浪波傾角與減搖前、后船舶橫搖角的曲線。

圖11 不規則波下海浪波傾角與船舶橫搖角（空載工況）Fig. 11 Wave slope and ship roll angle under irregular waves (noload draught)

從圖11 中可以看出，半潛船在空載工況不規則波海浪下，減搖前船的橫搖角為11.38°，減搖后為7.88°，此時減搖水艙內的液位幅值變化較大，說明在此工況下船舶的橫搖運動較劇烈。通過計算，可得此時無擋板的減搖水艙在不規則波下的減搖效果為30.88%。

圖12 所示為船舶滿載工況下不規則波時海浪波傾角與減搖前、后船舶橫搖角的曲線。

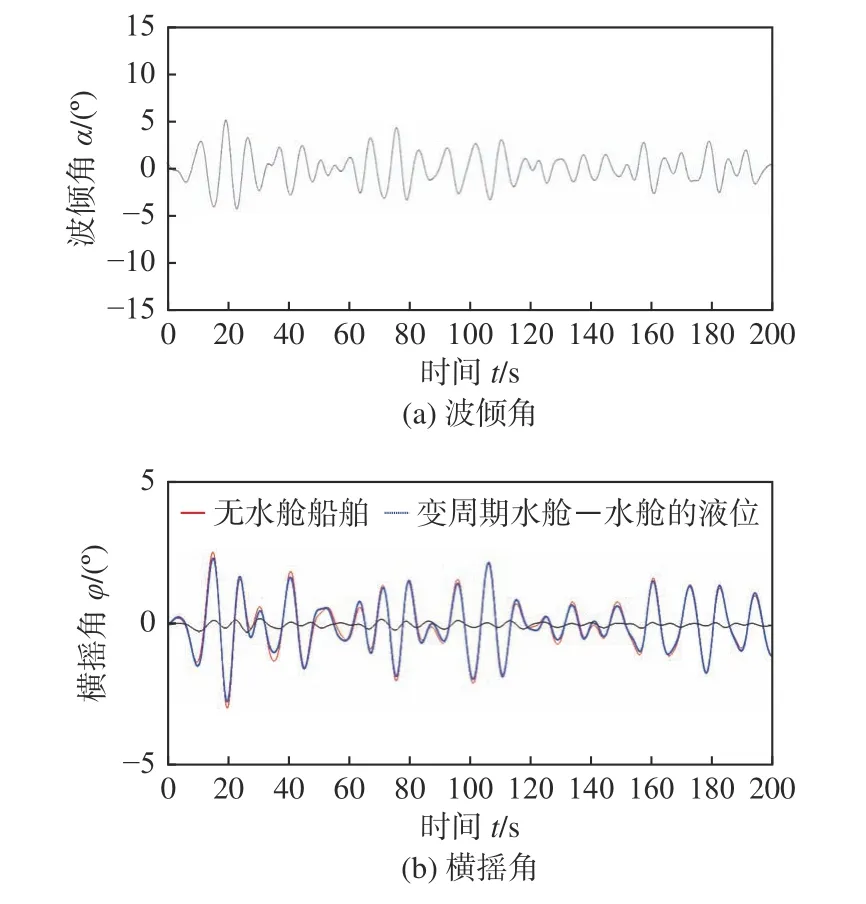
圖12 不規則波下海浪波傾角與船舶橫搖角（滿載工況）Fig. 12 Wave slope and ship roll angle under irregular waves (load draught)

由圖12 可以看出，半潛船在滿載工況時為水下工作狀態，船舶自身的橫搖運動不如之前2 種工況下的橫搖運動劇烈，此時，不規則波海浪下減搖前船舶的橫搖角為2.26°，裝置加了水艙之后為2.16°。通過計算，可得具有5 個T 型擋板數量的減搖水艙在不規則波下的減搖效果為4.42%。

綜合上述仿真結果， 可見本文所提可變周期被動式減搖水艙可以通過改變T 型擋板的數量來調整減搖水艙的周期，以使水艙的固有周期與船舶的周期相互匹配，從而更好地適應船舶的不同工況狀態，并為此提供良好的減搖能力，提高船舶在海上航行時的穩定性，進而增加船上工作人員和運輸貨物的安全性。

5 結 語

本文針對半潛船的3 種主要工況（半載、空載、滿載）會導致其橫搖周期變化較大的特點，初步設計了具有4 種不同T 型擋板數量的減搖水艙結構，并通過Fluent 仿真軟件分析了不同數量T 型擋板結構對延長水艙周期的影響。仿真數據表明，針對該尺寸的水艙，每增加一對T 型水艙，水艙固有周期約增加4 s，因此適用于橫搖周期變化較大的船舶。

隨后，采用AR 模型對船舶橫搖周期進行了預報，并將預報的橫搖周期作為控制信號來控制水艙內擋板的高度，改變其工作數量，進而調整水艙的固有周期，以使水艙周期與船的周期相匹配。仿真結果表明，船的減搖效果較好。

后續，還需進行半潛船模實驗，以驗證不同T 型擋板數量下可變周期被動式減搖水艙的減搖效果與仿真實驗是否一致。