一種航天器返回覆蓋區面積快速計算方法
淡 鵬, 何雨帆, 陳俊收
(1.宇航動力學國家重點實驗室, 西安 710043; 2.西安衛星測控中心, 西安 710043)
1 引言
航天器升力式再入返回[1-2]地球過程中可通過主動控制傾側角和速度攻角來調節飛行過程中的升力和阻力,使其獲得較大的橫向和縱向機動能力[3]。 為了衡量航天器再入飛行的機動性能或尋找合適的安控時機,常常需要實時計算飛行過程中的覆蓋范圍(例如飛行過程的可達區、濺落區等)及其相關幾何參數[4]。
航天器再入飛行的覆蓋范圍定義了航天器潛在的覆蓋區域[4-6],可為航天器再入飛行任務規劃提供關鍵信息,同時可幫助航天器在正常的再入飛行和突發故障時變更或選擇潛在的著陸位置。 在覆蓋范圍分析時需要實時計算該覆蓋范圍與特定的區域(如期望的落點限制區域、國境線、海域等)相交部分的面積或面積占比等參數,以便對當前飛行能力及飛行的安全性進行實時評估。 此類計算實質上可轉化為計算球面上不規則多邊形區域的面積以及多個多邊形相交部分求解等問題。 最常見的多是二維平面上的算法。 例如葛偉華等[7]基于邊界跟蹤方法實現了一種平面上的區域面積計算方法;齊澄宇等[8]在GeoST 全球參考網格基礎上,設計了一種可以擺脫經緯度和積分運算的面積計算方法。 這些方法主要針對平面圖形,應用到球面時誤差擴大。 對球面上的計算問題,王會然等[9]利用圖斑橢球和高斯投影方法減小了面積計算的誤差;Kumar 等[10]給出了一種采用近似展開公式計算橢球面上面積的方法。 但以上方法還稍顯復雜,編程實現有部分難度。
多邊形相交區域面積計算是該問題更深層次的計算,它需要首先找出不規則區域的相交部分,然后再計算出面積等參數。 針對該問題,朱磊等[11]提出了一種平面上相交面積計算的雙向鏈表算法;汪榮峰等[12]基于多邊形的交、差運算,將覆蓋多邊形進行分解和三角化,采用統計算法實現了一種基于多邊形布爾運算的相交面積計算方法。 但以上方法實現時還不夠簡便,對于覆蓋區面積占比計算時的實時性有待進一步提高。
考慮到航天器再入飛行過程中,為了及時尋找合適的安控時機,覆蓋區面積及占比計算常常需要較高的實時性和對各種不規則形狀的適應能力,需要快速對航天器進行飛行狀態的判斷。 因而需要研究一些誤差較小、實現過程簡潔、實時性高、可靠性強,且支持復雜幾何邊界和易于工程應用的計算方法。 本文提出的方法與常用的經度、緯度二維方向網格劃分算法[13]不同,僅在緯度方向進行一維分割的區域面積及面積占比計算。 該方法直接建立在球面而非平面形狀之上,利用球冠面積公式和弧段張角的統計思路,實現覆蓋區相交部分面積及面積占比的快速估計。
2 覆蓋區相交面積及占比快速估計
在航天器返回覆蓋區與特定區域(此處以極不規則的國境線為例)相交部分的面積及面積占比快速估算中,傳統的網格劃分算法[13]因為要進行經度、緯度二維方向上的劃分,使得分割塊數較多時,計算的復雜度成二次方增長,計算速度明顯下降,因而較難滿足實時性的要求。 本文對其進行改進,只在緯度方向上進行分割,使計算復雜度降低了1 個維數,相較于網格算法的計算速度有較大提升。
計算覆蓋區相交面積的算法流程如圖1所示。

圖1 覆蓋區相交面積計算流圖Fig.1 Flow chart for calculating the intersection area of landing footprint
2.1 界線數據的準備
航天器返回覆蓋區進入國境內部分面積及面積占比計算中需要用到2 個球面多邊形,分別是地面覆蓋區域邊界多邊形和國境線多邊形。
設2 個多邊形分別用一系列逆時針順序排列的多個點表示。 其中,地面覆蓋區域邊界多邊形頂點個數為n0,國境線多邊形頂點個數為n1。 設地面覆蓋區域邊界多邊形頂點序列為p0,p1…pi…pn0( 0 ≤i 為方便后續計算,可事先統計出國境線多邊形點序列χ1的經度及緯度的值域(即最大值和最小值),設國境線多邊形經度取值范圍為[α1min,α1max] ,緯度取值范圍為[β1min,β1max] 。 對某個時刻航天器地面覆蓋區多邊形的點序列χ0,統計其邊界點經度及緯度取值范圍(最大值和最小值)。 設統計出的地面覆蓋區域邊界點經度范圍為[α0min,α0max] ,緯度范圍為[β0min,β0max] 。 據此,可先對地面覆蓋區域與國境線相交的可能性進行粗判斷。 若β0min≥β1max,則無相交區域;若β0max≤β1min,則無相交區域;若α0max≤α1min,則無相交區域;若α0min≥α1max,則無相交區域。 無相交區域時,航天器返回覆蓋區進入國境線內部分的面積占比為0,面積也為0。 對航天器返回覆蓋區的球面多邊形進行緯線分割,將覆蓋區緯度取值范圍[β0min,β0max] 等分為n份(n為事先給定的等分份數,例如取1000)。 如圖2 所示(圖中多邊形為一個覆蓋區多邊形示例),這樣就形成了n個環狀緯度分割帶。 圖2 球面緯線等分示意圖Fig.2 Diagram of dividing latitude line on sphere 設地面覆蓋區域緯度取值范圍中各條等分線上的緯度值依次為β0、β1…βn。 其中第i(0 ≤i 考慮到此處對緯度進行的是n等分,則任意相鄰2 條緯度等分線間的緯度差是相同的,即有βi+1-βi=(β0max-β0min)/n。 同時,由球冠面積公式可推導出i和i+1 條緯度線之間的整個環狀緯度帶區域的面積為Si=2πR2×(sinβi+1-sinβi) 。其中,R為地球半徑。 圖3 所示為當n足夠大時,對某一個緯度環狀帶,2 條緯度線長度足夠接近,緯度圈單位圓心張角上梯形部分的面積可近似為式(1)所示。 圖3 緯度環狀帶示意圖Fig.3 Schematic diagram of the latitude ring 即當n足夠大時,若能統計出該緯度圈在某個區域內的圓心張角之和,即可快速估算出該區域內部分的面積近似值。 由此可見,對第i個緯度環狀分割帶,可通過統計其在覆蓋區內部分的緯度圈圓心張角之和(記為κi)即可得到該部分的面積,同樣通過統計在覆蓋區與國境線共有部分的緯度圈圓心張角之和(記為μi)就可得到相交部分的面積。 通過對各個緯度分割帶的累加即可得到整個地面覆蓋區面積、覆蓋區進入國境內部分的面積。據此可得出地面覆蓋區面積為式(2)所示。 覆蓋區在國境線內部分區域的面積為式(3)所示。 這樣就可得到地面覆蓋區進入國境內部分區域面積占比的快速計算公式為式(4)所示。 本文方法僅僅進行了緯線方向的分割,而沒有進行經線方向分割,因而相對于傳統的網格式分割算法,計算速度大幅度得到提升。 對圖3 所示的地面覆蓋區域緯度范圍進行n等份分割,依次掃描每一個緯度分割帶。 統計第i和第i+1 條緯度等分線的中間線在地面覆蓋區內、覆蓋區與國境線相交部分內的緯度線圓心張角和(即經度跨度)。 圖4 給出了第i和第i+1 條緯度等分線的中間線與球面多邊形某部分邊的相交關系示意圖。 圖4 緯線分割帶與多邊形邊相交示意圖Fig.4 Schematic diagram of the intersection of latitude dividing zone and the polygon 在緯度線圓心張角之和統計時,可從覆蓋區及國境線球面多邊形左側向右掃描目標緯度線(中間緯度線),計算相應部分的圓心張角之和。 由覆蓋區經度最小值α0min、國境線經度最小值α1min,可得兩者的經度最小值為α′min=min(α0min,α1min) ,則此中間緯度線上左側點的經度可取為α′min-τ(τ為事先給定的大于零的值,如取1.0,以保證該點在2 個多邊形之外),緯度值為β′i。 計算該左側點向右發出的中間緯度線與覆蓋區的交點坐標,因該左側點在覆蓋區及國境線多邊形的外部,則中間緯度線與覆蓋區多邊形交點個數必為偶數(或無交點)[14-15]。 計算時可逆時針方向遍歷覆蓋區邊界多邊形的各條邊,然后計算與各邊的交點(有時2 條邊的交點可能相同),形成1 個交點序列。 設該中間緯度線與覆蓋區多邊形交點序列(記為序列χ2)為p20,p21,…,p2i,…(交點的總個數取決于在該緯度線上的邊數),計算每2 個交點(如p20與p21,p22與p23,…)之間的弧線對應的緯度圈圓心張角(即這2 個點的經度之差,因為緯度線上各點的緯度值是相同的),然后對每2 個點的經度差進行累加,即得到κi(該緯度線在覆蓋區內的弧段的緯度圈圓心張角之和)。 如圖4 所示,某個中間緯度線與多邊形部分邊形成了A-F共6 個交點,圖中紅色弧線部分為被邊切割后在多邊形內的弧段。 將這幾個累加就可得到κi。 同理,可計算出該向右的中間緯度線與國境線多邊形的交點序列(記為序列χ3),將各交點標記為p30,p31,…,p3i,… (交點的總個數取決于在該緯度線上的邊數)。 下面需要計算該向右的緯度線在覆蓋區與國境線共有部分的弧段的緯度圈圓心張角之和對應的緯度圈張角度數和μi。 具體方法為:通過計算序列χ2中每個交線弧段(向右緯度線與覆蓋區每2 個交點間的弧段)與序列χ3中每個交線弧段(向右緯度線與國土邊界線每2 個交點間的弧段)共有部分的弧線的緯度圈圓心張角后,進行累加即可。 如對χ2中弧段1[p20,p21],設2 個點經度分別為α20、α21,與χ3中弧段2[p30,p31],設經度分別為α30、α31,因各點的緯度相同,只需要對經度值作簡單地大小比較,即可得到共有部分弧線的張角。 具體地,當弧段1 給定時,弧段2 與其有以下幾種關系。 圖5 所示即為2 個弧段可能的關系圖,需要說明的是弧段1 與弧段2 實際在同一緯度,此處為了表述清晰對其在上下方向進行了平移。 1)若弧段2 左端點在弧段1 左側,則根據其右端點的位置不同,兩者可能的位置關系如圖5(a)所示; 2)若弧段2 左端點在弧段1 內部(包含兩端點),則兩者可能的位置關系如圖5(b)所示; 3)若弧段2 左端點在弧段1 右側,則兩者可能的位置關系如圖5(c)所示。 從圖5 可見: 1)若α21≤α30,弧段1 與弧段2 無共有弧段; 2)若α20≥α31,弧段1 與弧段2 無共有弧段; 3)其他情況時,弧段1 與弧段2 的共有弧段的圓心張角為min(α21,α31)-max(α20,α30) 。 這樣就計算出了這2 個弧段的共有部分的緯度線圓心張角。 通過累加這些圓心張角即可得到交集部分的緯度線圓心張角之和μi,再由公式(2)~(4)就可得到完整的緯線掃描算法。 為了驗證本文算法的可行性,進行仿真試算。算例1:采用緯線掃描算法的公式(2)計算德國國境線(大陸部分,不含任何島嶼)內區域面積(圖6 中連線繪制的曲線部分),該國境線為極不規則的多邊形。 在緯線掃描計算時,對緯度方向進行1000 等份分割,計算結果為35.32 萬km2,這與公開的德國大陸部分面積(約34.93 萬km2,數據來源:維基百科)相近,誤差約為1.1%,說明算法是可行的。 圖6 覆蓋區與德國邊境線相交示意圖Fig.6 Schematic diagram of the intersection of landing footprint and German border 算例2:仿真給定一覆蓋區多邊形區域(圖6中散點繪制的曲線部分),計算其進入德國大陸邊境線內區域面積以及該面積與整個覆蓋區面積的比值。 同時采用網格分割算法[13]進行計算比較,網格分割算法方法將球面多邊形在經度、緯度方向進行等間隔分割,并計算各網格的面積,然后累加出覆蓋區及其與國境線交集部分面積。 計算所用計算機為賽揚雙核2.2 GHz 的CPU,4GB 內存,32 位的Win7 操作系統。 因覆蓋區及入境部分無準確的參考面積,故此處只對2 種算法計算情況進行對比,算法對比結果見表1。 表1 給出了各算例計算的覆蓋區面積、入境部分面積占比(百分比)以及計算耗時。 表1 各算例計算結果Table 1 Calculation results of each example 本算例中,覆蓋區邊界由234 個點組成,德國大陸界線由1612 個點組成;本文緯線掃描法計算時對覆蓋區進行1000 等份分割,網格算法在經緯度方向各進行1000 等份分割; 為了考察本文算法精度影響因素,算例2 基礎上繼續給定以下算例。 算例3:在算例2 基礎上將覆蓋區邊界點數減少一半(實際使用117 個點),其他條件保持不變。 算例4:在算例2 基礎上將德國大陸界線點數減少一半(實際使用806 點),其他條件保持不變。 算例5:在算例2 基礎上對覆蓋區進行900等份分割,其他條件保持不變,同時使用經、緯度方向各900 等份劃分的網格算法。 算例6:在算例2 基礎上對覆蓋區進行500等份分割,其他條件保持不變,同時使用經、緯度方向各500 等份劃分的網格算法。 算例7:在算例2 基礎上對覆蓋區進行100等份分割,其他條件保持不變,同時使用經、緯度方向各100 等份劃分的網格算法。 算例8:在算例2 基礎上對覆蓋區進行50 等份分割,其他條件保持不變,同時使用經、緯度方向各50 等份劃分的網格算法。 算例9:在算例2 基礎上對覆蓋區進行10 等份分割,其他條件保持不變,同時使用經、緯度方向各10 等份劃分的網格算法。 從算例2 可見,當進行1000 等份分割時,本文算法耗時只有網格方法的0.22%,入境部分百分比約相差0.1%。 從算例2、3 可見,覆蓋區邊界點從234 減少到117 時,覆蓋區面積發生變化,但入境面積占比變化不明顯,這是因為此覆蓋區圖形相對較平滑,點數減少一半后形狀變化不明顯。 算例4 中德國大陸界線點從1612 減少到806,覆蓋區點不變時,本文算法耗時約減少1/3,可見對于點數過多的邊界線數據,適當減少點數可提高計算效率。 從算例5~9 可見,當覆蓋區、邊界點數保持不變時,通過改變緯度劃分段數,可有效提高計算效率,但面積精度變化較大,段數太少時面積精度過低。 在上述算例中,本文算法耗時都在0.4 s 以下,耗時明顯比網格分割算法少,滿足實時性要求。 各算例中,相對于網格算法,本文算法計算的入境部分面積占比的誤差均在0.2%以內,算法可行。 1)本文通過將傳統的經緯度二維方向劃分算法降維處理,僅在緯線方向上進行分割,并擴展到球面上,形成了一種再入覆蓋區相交面積及面積占比的快速計算方法,仿真結果表明本文方法可行,計算速度滿足實時性要求。 2)本文算法在具體實現中進行了部分近似,需滿足精度要求時緯線分割數目不能太少,下一步將重點在保證實時性前提下對提高算法精度進行研究。2.2 覆蓋區與國境線關系粗判斷
2.3 球面緯線分割





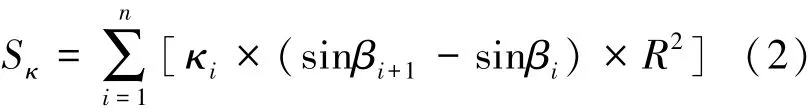


2.4 緯線掃描比較計算相交區域

3 仿真分析


4 結論

