基于改進型變步長與模糊控制的MPPT控制策略

程 超

（安徽淮南平圩發電有限責任公司發電部，淮南232038）

近幾年，科研人員對太陽能光伏發電系統最大功率點跟蹤（Maximum Power Point Tracking，MPPT）開展了創新和研究，提出了較多的控制策略［1-2］。根據現實的機制與控制算法特點特征，可分為3類：基于優化數學模型的間接控制策略、基于采樣數據的直接控制策略與基于先進控制理論的MPPT算法策略。

（1）基于優化數學模型的間接控制策略。包含：短路電流系數法、恒定電壓法、開路電壓系數法［3-4］。恒定電壓法，主要是在溫度恒定時，太陽能光伏電池會隨著光照強度的變化對外輸出單峰值特性的功率曲線，而這時太陽能電池將工作在最大功率點上。但太陽能光伏電池對外部溫度的要求比較苛刻，一旦外部的溫度發生突變，將會對系統帶來較大的誤差。短路電流系數法和開路電壓系數法原理相同，均是在恒定電壓法上進行優化，主要是應對溫度變化帶來的偏差；但不足之處在于需要周期性地開斷負載和太陽能光伏電池，檢測開路端電壓，這會造成一定的功率損耗，得出的并不一定是最大功率。

（2）基于采樣數據的直接控制策略。包含：擾動觀察法、電導增量法等，這一類控制策略需要連續采集相關太陽能電池的端電流和端電壓，利用采樣的數據直接控制對應系統工作點，其魯棒性能較好，精度較高［5-6］。兩者共同之處是對太陽能電池的輸出電壓不間斷地施加擾動追蹤最大功率點，差別在于電導增量法一旦到達了最大功率點就不需要給予擾動。

（3）基于先進控制理論的MPPT算法策略。這一類控制算法特點是以最新控制理論基礎為前提，對于太陽能光伏發電系統功率輸出的時不變性與強非線性特點，提出了新的控制算法，比如模糊控制算法、滑模控制、神經算法等［7-9］。神經算法運用在MPPT上有較高的精度，但需要大量地訓練光伏電池板的輸入輸出參數，才能獲得相應的控制規則，若電池板不同，參數變化，訓練操作就會繁瑣。滑模控制結構的變量為S，若S<0，則滑模輸出變量Uh=1；若S>0，則Uh=0。利用開關變化的特點，強迫系統在允許范圍內的軌道周邊做高頻率、小幅度的滑模上下運動，以此保持并運行在預設的滑動曲面上。

光伏發電系統的輸出特性易受外界影響而出現非對稱的強非線性特征，輸出的功率會偏離最大輸出功率點。針對這一問題，本文分析了MPPT的幾種常用控制策略的優缺點，在上述分析基礎上作進一步改進，通過變步長算法先對光伏電池的輸出功率進行迅速跟蹤，并采用模糊控制策略對其進行二次優化鎖定跟蹤，以此減少響應時間與振蕩，提升光伏發電系統的穩定性。

1 光伏電池輸出特性

光伏電池是通過其半導體材質實現光能的物化反應，將太陽的光能轉化為電力能［10-11］。太陽能光伏發電等效電路如圖1所示。其中，Ipv為光伏電池輸出電流；Iph為光生電流；Rsh為等效并聯電阻；Rs為等效串聯電阻；I0為二極管半導體的反向飽和電流；RL為外接負載電阻；Ish為等效并聯電流；UD為暗電壓，即光伏電池在無光環境下由外電壓作用內部PN結所流通的單向電壓；C為電容；Upv為光伏電池的輸出電壓。隨著工作溫度、太陽光照強度等外界環境的變化，太陽能發電存在間歇性、非線性的現象。

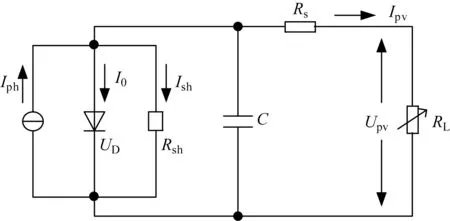
圖1 太陽能光伏發電的等效電路

圖1對應數學模型方程為

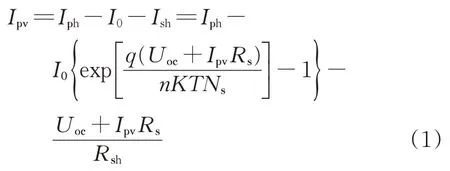
式中：Uoc為電陽能光伏電池的開路電壓；Ns為串聯電池數；K為玻爾茲曼常數，一般取1.38×10-23J；T為絕對溫度；n為光伏電池的數量；q為單位電荷數。

實際太陽能光伏電池工作時，隨著太陽光照強度的變化，會對輸出電流影響較大，不能得到精確數據。因此，在實際工作中常采用工程型的太陽能光伏電池模型，即

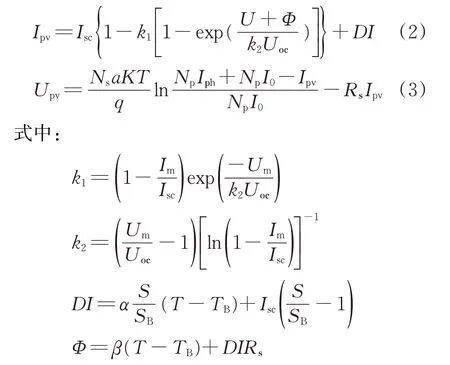
Isc為短路電流；k1為偏差電流的校正系數；k2為偏差電壓的校正系數；U為光伏電池輸出電壓；Φ為校正后的電壓偏差值；D為導通占空比；I為輸出電流；Np為太陽能電池組件并聯數；a為校正系數；SB為標準光照輻射強度；TB為環境溫度；α為電流的溫度系數，A/℃；β為電壓溫度系數，V/℃；S為現實工作光照輻射的強度；Um為光伏電池在最大功率點的電壓；Im為光伏電池在最大功率點的電流。

太陽能光伏電池的輸出功率為

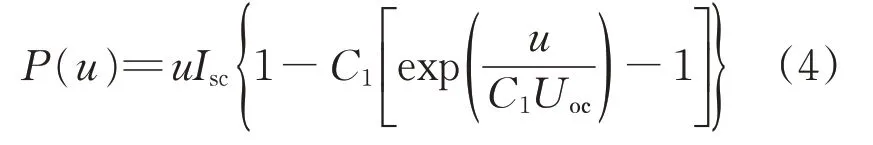
式中：u為光伏電池實際輸出電壓；C1為并聯電容。

由式（2）~（4）模擬經驗函數曲線，選取光伏電池相關的仿真參數。具體建模參數分別如表1和表2所示。其中，Pmax為最大功率。

表1 光伏陣列工程參數

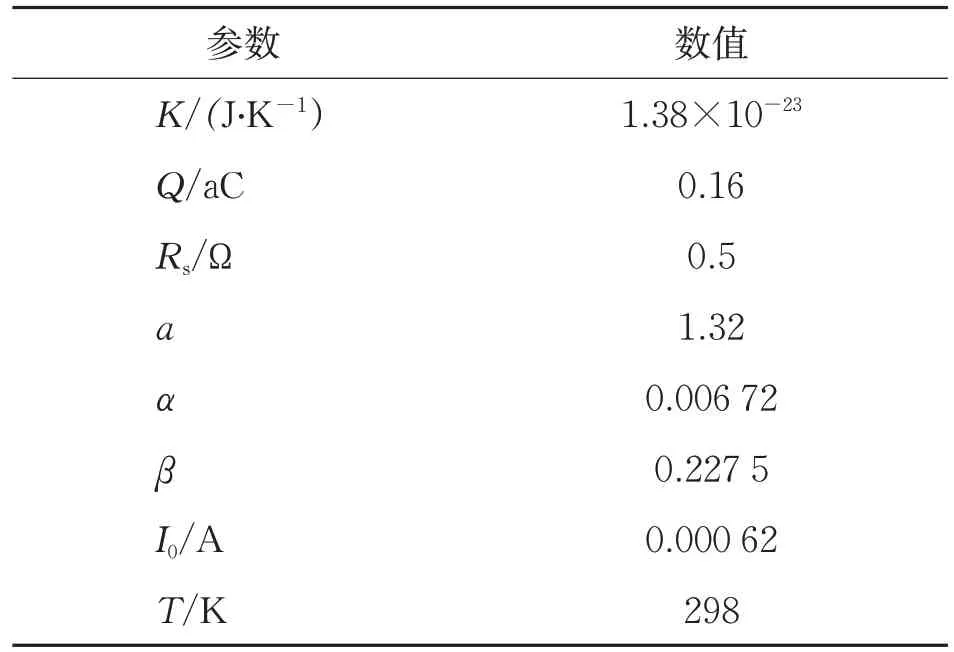
表2 光伏陣列仿真的擬合參數

2 變步長部分

傳統定步長響應速度及跟蹤精度都有一定程度缺點，科研人員大多采用變步長的控制策略［12-13］，一般分為兩種：

（1）依據相關光伏輸出功率的一次導數值大小，賦予快慢不同的步長值。

（2）將光伏輸出功率的一次導數P'（u）作為擾動變步長的參數，由此步長將在最大功率點兩側做自適應性的相關調整。比如，若工作于最大功率點左側，則進行正向擾動；若在最大功率點右側，則反向擾動；當接近最大功率點時，步長會自動變小。

對光伏輸出功率P（u）進行一階求導，可得P'（u）數學表達式為

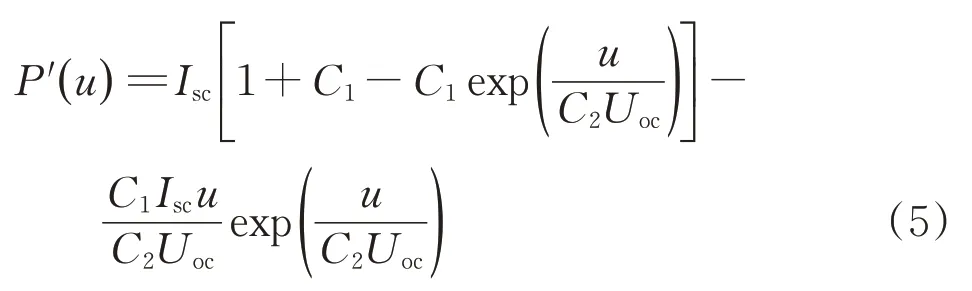
式中：C2為串聯電容。

標準測試狀況下，P'（u）若工作在最大功率點左側，P'（u）為正；若工作在最大功率點右側，P'（u）為負。這與擾動方向的要求基本吻合，且左右側是∣u-Um∣單調減函數，符合步長變化的參數要求。

第k個周期的占空比為

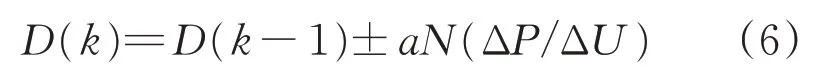
式中：N為調整變步長的系數，一般的變步長算法中，N就是P'（u）；ΔP為輸出功率的變化量；ΔU為輸出電壓的變化量。

本文優化的變步長部分，取N=arctan［P'（u）］，a按照實際較大的輸出特性取值。

變步長參數的變化率如圖2所示。變步長系數N的一階導數，依照高等函數中的反三角求導公式計算如下：

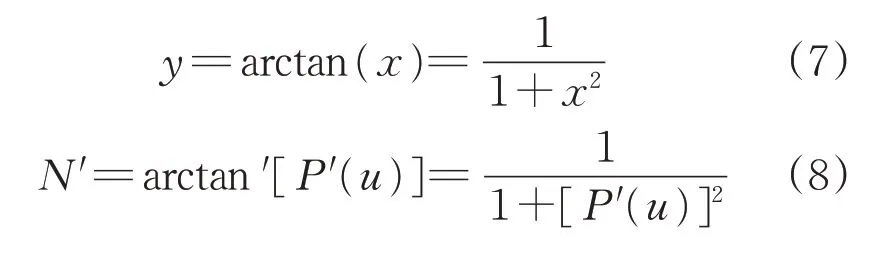
圖2 變步長參數的變化率

本文為了取得更好的效果，將變步長和非對稱的模糊控制相結合。當光伏輸出工作在遠離最大功率點時，優化的變步長會使其迅速靠近最大功率點，但當逐步接近最大功率點預設的核心范圍區間時，通過非對稱的模糊邏輯控制對其進行尋優。

3 模糊部分

太陽能光伏發電的輸出特性曲線不易用精準的數學模型表示，因其具有較強的非線性特征。太陽能光伏電池的MPPT也不需要特別的光伏電池模型，只需要不斷地調整可控參數值，使其輸出特性曲線逐漸靠近最大功率點。該過程符合對于被控目標對象的模糊控制特征。因此，對于太陽能光伏電池的MPPT采用模糊控制相對合適［13-14］。圖3所示為非對稱模糊控制策略框圖。

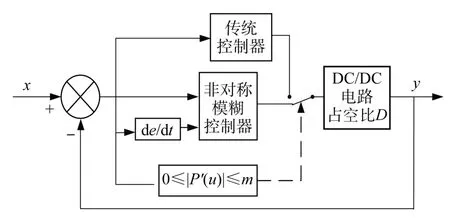
圖3 非對稱模糊控制策略框圖

模糊PI參數的自整定結構框圖，如圖4所示。

圖4基本原理是：先將實時檢測的系統并網電流的每個周期里的數值igrid，與規定的電網電流值iref作比較，得出誤差信號e，然后將誤差信號e依次輸入到模糊控制器與PI控制器中。模糊控制器依據相應的模糊規則輸入誤差的變化率與輸入誤差，將輸出變量ΔKp與ΔKi輸入到PI控制器中，分別與預先設定好的比例系數Kpo、積分系數Kio進行計算，從而達到實時調整的效果。

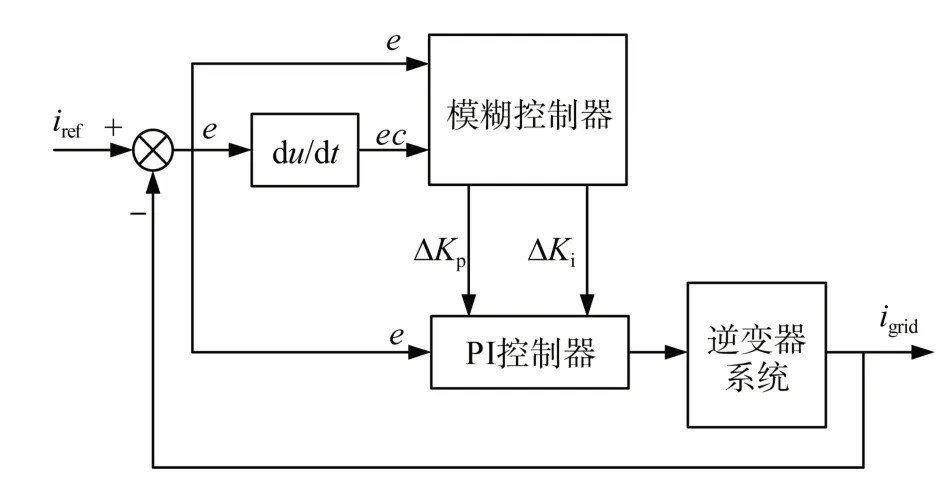
圖4 模糊PI參數的自整定結構框圖

模糊PI參數自整定的計算式為

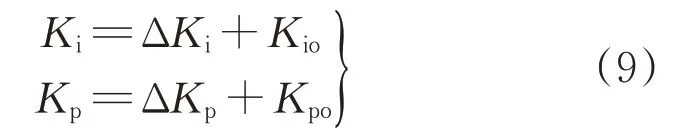
通過模糊PI參數自整定，找出PI的兩個參數Kp、Ki與誤差e、誤差變化ec之間的模糊關系。運行中不斷檢測e和ec，根據控制原理對兩個參數在線修改，以滿足e和ec不同時對控制參數的要求，從而使系統具有良好的動、靜態性能。在線運行時，控制系統通過對模糊邏輯規則的結果處理、查表和運算，從而完成對PI參數的在線調整。具體的工作流程如圖5所示。其中，r（k）為第1個輸入因變量；y（k）第2個輸入因變量。

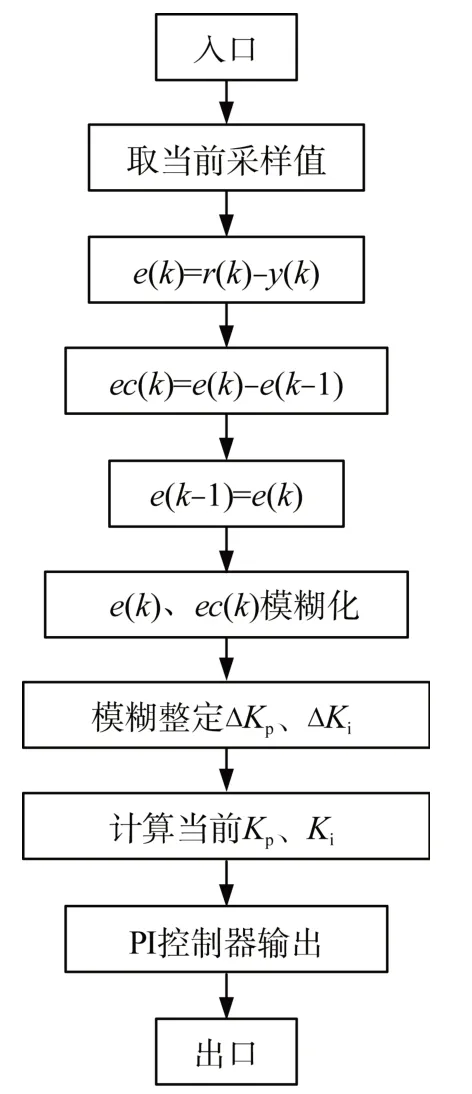
圖5 模糊PI工作流程圖

本文利用Matlab/Simulink工具箱實現模糊PI控制。該工具箱具有簡單易懂，方便調節參數的特點。按照模糊PI整定規則設置模糊工具箱，隸屬度函數選為三角函數，誤差e和誤差的變化率ec的論域分別為［-150，150］、［-3.5，0.5］，輸出的模糊規則圖形如圖6、圖7所示。

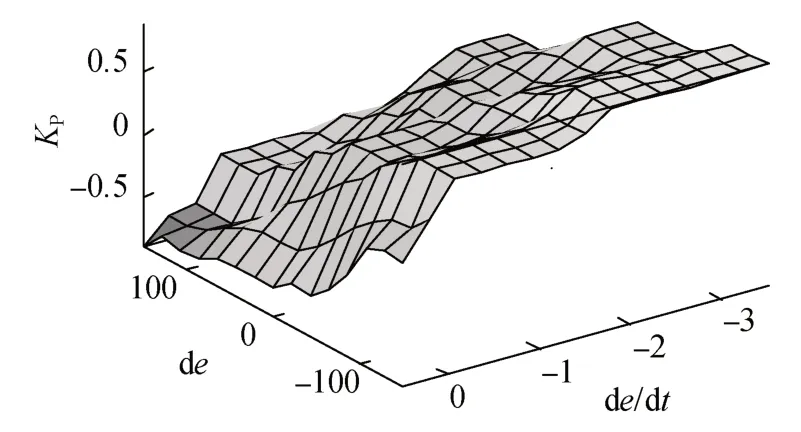
圖6 輸出量ΔK p的模糊規則圖形

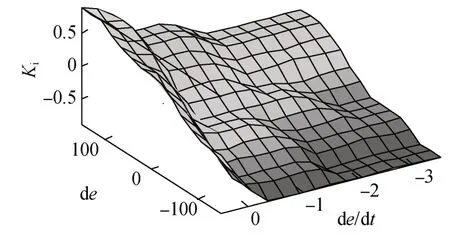
圖7 輸出量ΔK i的模糊規則圖形

4 仿真與分析

在Matlab/Simulink中建立仿真模型，仿真模型由光伏電池、Boost電路及電阻性負載組成[15]。部分參數為：太陽能光伏電池最大電流Isc=3.5 A，最大功率點的電流Im=3 A，最大輸出電壓Uoc=600 V，最大功率點的電壓Um=380 V，電阻R=100Ω。模糊PI控制器初始參數Kp=4.5，Ki=20.5。光伏發電系統中兩個電容值從左到右依次為10μF、1μF，電感L值設為0.2 H，采用ode45算法仿真。設定光伏電池面板溫度T=25℃，光照強度S由1 kW/m2驟升至1.2 kW/m2再驟降至800 W/m2，分別對定步長、變步長[11]和改進的變步長的MPPT技術進行仿真。仿真結果如圖8所示，光伏陣列各工作階段功率變化如表4所示。

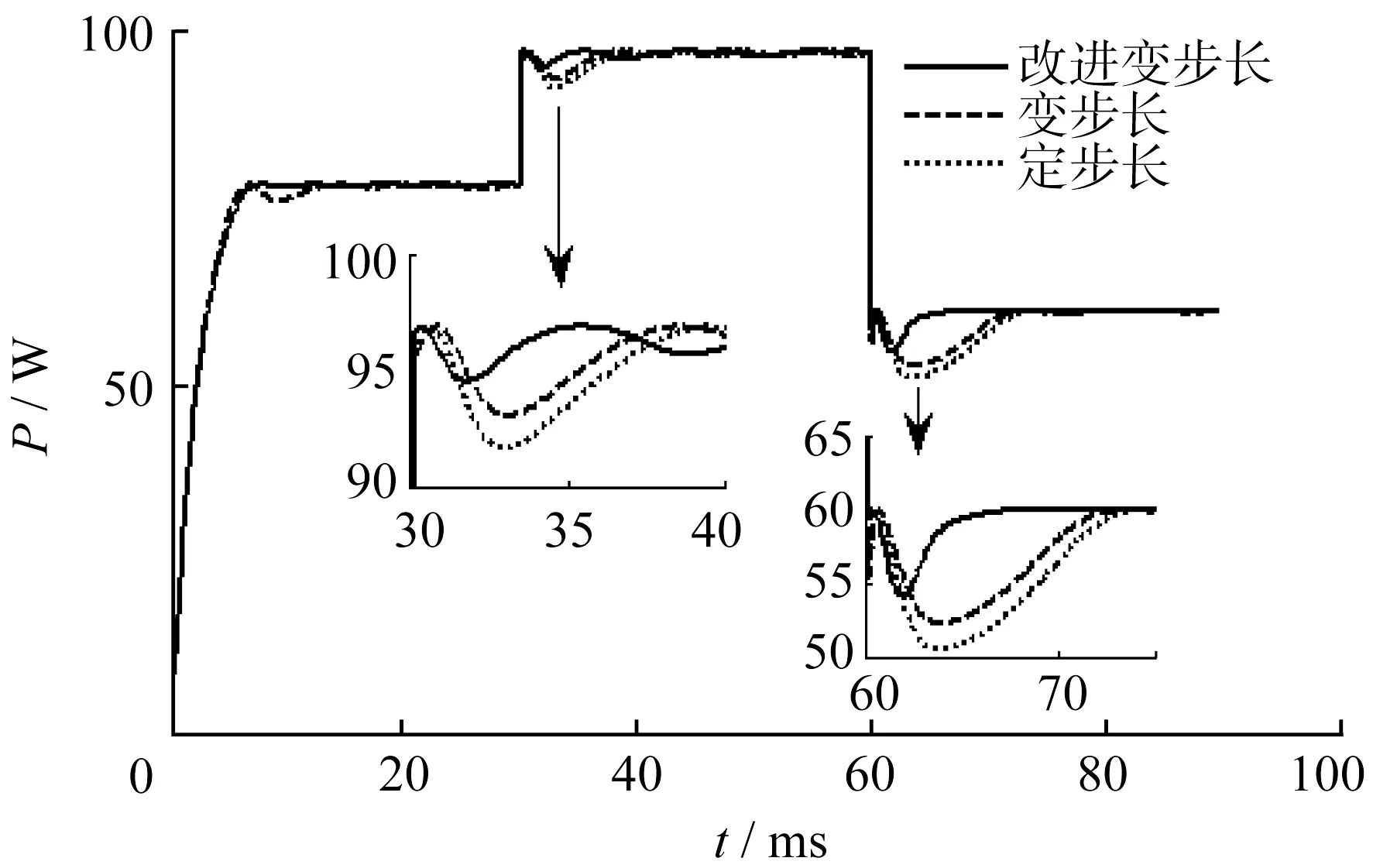
圖8 仿真結果對比圖

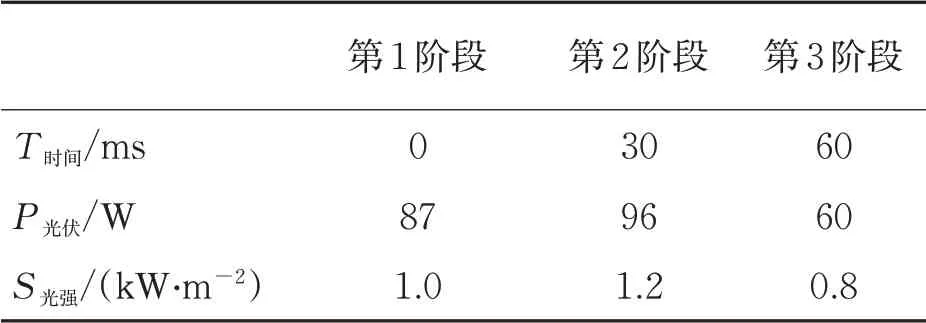
表4 光伏陣列各工作階段功率變化

由圖8與表4可知，第1階段，在0~30 ms時段，光伏系統功率約為87 W，光照強度為1 kW/m2；第2階段，由于在第30 ms時刻，調節擾動使得光照強度上升到1.2 kW/m2，光伏發電功率在30 ms時刻迅速增加至96 W；接著，第3階段，在60 ms時刻，通過調節擾動使得光照強度下降到800 W/m2，負荷功率在60 ms時刻下降到60 W。

通過圖8對比兩張局部細節圖，能夠明顯看出采用結合后的優化變步長和非對稱模糊控制MPPT算法可以較好地追蹤到最大功率點；當太陽能光伏板開始工作時，兩種控制策略都可跟蹤到最大功率點。然而，優化后的變步長和非對稱模糊MPPT控制算法運行更平穩，無較大的振蕩，當外部光照強度環境參數發生改變時，太陽能光伏發電系統也可以迅速而精確地追蹤到最大功率點，表現出良好的穩定性。整個過程中，采用結合后的優化變步長和非對稱的模糊控制算法比傳統的定步長MPPT控制策略優異些。

5 結 論

基于傳統變步長在光伏發電的最大功率點附近出現的振蕩，以及前期跟蹤精度不足的現狀，針對性地提出采用非對稱模糊結合優化變步長參數的新型控制策略方法，并在Matlab上進行驗證仿真。研究表明，該新型控制策略方法具有動態可靠性與優異性。在其他方面，對大功率、多種電源形式的并網發電系統，有待進一步研究。