多星敏感器協(xié)同觀測(cè)的短弧關(guān)聯(lián)算法

黃秋實(shí)，張雅聲，馮 飛

(1.航天工程大學(xué) 航天指揮學(xué)院，北京 101400；2．中國(guó)人民解放軍61646部隊(duì)，北京 100085)

隨著航天器和空間碎片的增加，日益擁擠的空間環(huán)境成為各國(guó)爭(zhēng)相搶奪的寶貴戰(zhàn)略資源，其中地球同步軌道(GEosynchronous Orbit，GEO)的衛(wèi)星往往承擔(dān)著通信、導(dǎo)彈預(yù)警、數(shù)據(jù)中繼、廣播等重要任務(wù)，具有極高的戰(zhàn)略價(jià)值[1]。對(duì)地球同步軌道目標(biāo)的監(jiān)視是空間態(tài)勢(shì)感知的重要一環(huán)，關(guān)系著國(guó)家的太空安全。目前，中國(guó)對(duì)地球同步軌道目標(biāo)的探測(cè)及監(jiān)視主要依賴于地基光學(xué)監(jiān)視系統(tǒng)[2]，地基監(jiān)視系統(tǒng)工作會(huì)受到大氣及氣象條件的影響，無(wú)法全天時(shí)觀測(cè)，特別是由于地理和政治因素，中國(guó)不具備美國(guó)的全球布站條件。相比于地基觀測(cè)，天基監(jiān)視系統(tǒng)不受大氣、地理位置的制約，具有觀測(cè)距離遠(yuǎn)、設(shè)備復(fù)雜度低、功耗小等優(yōu)勢(shì)[3]。美國(guó)以光學(xué)衛(wèi)星組網(wǎng)構(gòu)建天基空間目標(biāo)監(jiān)視系統(tǒng)(Space-Based Surveillance System，SBSS)[4]，耗資巨大。中國(guó)的天基目標(biāo)監(jiān)視系統(tǒng)有待發(fā)展。基于星敏感器的空間目標(biāo)泛在感知即挖掘星敏感器在定姿任務(wù)中拍攝的空間目標(biāo)信息，利用在軌衛(wèi)星數(shù)量多、星敏感器資源豐富的優(yōu)勢(shì)，在完成星敏感器定姿任務(wù)的同時(shí)實(shí)現(xiàn)對(duì)空間目標(biāo)的監(jiān)視[5]，可節(jié)約發(fā)射專用監(jiān)視衛(wèi)星組網(wǎng)的高昂成本。

圖1 多星敏感器協(xié)同觀測(cè)模型

星敏感器是一種高精度的衛(wèi)星姿態(tài)傳感器，同時(shí)具備光學(xué)元件。根據(jù)存儲(chǔ)的星表匹配星圖中的恒星，進(jìn)而確定衛(wèi)星的三軸姿態(tài)，定姿精度可達(dá)1″～3″。目前星敏感器僅作為姿態(tài)傳感器應(yīng)用于航天器。由于星敏感器不同于專用監(jiān)視衛(wèi)星，其固連安裝在衛(wèi)星本體無(wú)法主動(dòng)跟蹤目標(biāo)，但勢(shì)必存在多顆星敏感器視場(chǎng)交疊的時(shí)刻。此時(shí)，視場(chǎng)中出現(xiàn)的空間目標(biāo)處于多星敏感器的同步觀測(cè)下，如圖1所示。

文獻(xiàn)[5]提出一種基于星敏感器的空間目標(biāo)監(jiān)視網(wǎng)絡(luò)構(gòu)型，并通過(guò)仿真驗(yàn)證了多星敏感器同步觀測(cè)空間目標(biāo)的可行性。文獻(xiàn)[6]提出一種基于星敏感器僅測(cè)角數(shù)據(jù)的空間目標(biāo)定軌方法，該方法的前提是對(duì)多星敏感器在相同或不同時(shí)刻拍攝的空間目標(biāo)進(jìn)行關(guān)聯(lián)，將相同目標(biāo)的測(cè)角信息用于后續(xù)計(jì)算。當(dāng)前初始軌道的確定方法(比如改進(jìn)拉普拉斯方法)至少需要 3 min的連續(xù)測(cè)角數(shù)據(jù)方能定出較為精確的軌道。由于太空環(huán)境的復(fù)雜性，空間目標(biāo)的觀測(cè)受到光照、遮擋、噪聲等條件制約，將連續(xù)觀測(cè)時(shí)長(zhǎng)不足以確定空間目標(biāo)初始軌道的航跡段稱為短弧，其觀測(cè)時(shí)長(zhǎng)一般小于180 s。

文獻(xiàn)[7]中提出一種自適應(yīng)中值濾波方法，能夠較為有效地去除星圖中的椒鹽噪聲，并依據(jù)運(yùn)動(dòng)補(bǔ)償算法對(duì)星圖中的空間目標(biāo)、噪點(diǎn)、恒星進(jìn)行區(qū)分，提取空間目標(biāo)的質(zhì)心坐標(biāo)。文獻(xiàn)[8]中根據(jù)同一時(shí)刻下多星敏感器協(xié)同觀測(cè)幾何構(gòu)型與多目視覺(jué)類似，利用對(duì)極幾何原理實(shí)現(xiàn)空間目標(biāo)的同步關(guān)聯(lián)，在考慮星敏感器的抖動(dòng)、測(cè)角測(cè)距誤差、噪聲的基礎(chǔ)上，關(guān)聯(lián)準(zhǔn)確率可達(dá)90%。依據(jù)關(guān)聯(lián)結(jié)果，通過(guò)最小二乘法來(lái)求解空間目標(biāo)的坐標(biāo)。文獻(xiàn)[9]能夠以改進(jìn)拉普拉斯方法確定初始軌道的航跡，利用模糊關(guān)聯(lián)原理實(shí)現(xiàn)中斷航跡間的關(guān)聯(lián)。文獻(xiàn)[10]提出一種基于正弦擬合的空間目標(biāo)關(guān)聯(lián)方法，可區(qū)分來(lái)自不同軌道的空間目標(biāo)，但是航跡間隔超過(guò)3 h時(shí)關(guān)聯(lián)準(zhǔn)確率不高，對(duì)非地球同步軌道關(guān)聯(lián)效果并不好。

為解決光學(xué)測(cè)量短弧段的初始軌道估計(jì)問(wèn)題，MILANI等[11]提出了容許域的概念，將空間目標(biāo)按約束條件限制在由測(cè)量斜距、斜距變化率構(gòu)成的二維平面內(nèi)，平面中的每一點(diǎn)可代表一條軌道。文獻(xiàn)[12]通過(guò)對(duì)容許域進(jìn)行剖分，將其網(wǎng)格化，再?gòu)挠邢薜木W(wǎng)格節(jié)點(diǎn)搜索出目標(biāo)初始軌道，進(jìn)行目標(biāo)關(guān)聯(lián)。該方法有一些明顯的缺陷：容許域的約束條件較為寬松，搜索初始軌道過(guò)程繁瑣；在進(jìn)行多對(duì)多的空間目標(biāo)關(guān)聯(lián)時(shí)，軌道外推環(huán)節(jié)導(dǎo)致算法復(fù)雜度較高，運(yùn)行時(shí)間長(zhǎng)；在噪聲下空間目標(biāo)關(guān)聯(lián)的準(zhǔn)確率較低[12-13]。

筆者以上述研究為基礎(chǔ)，提出一種基于假設(shè)邊值的空間目標(biāo)短弧關(guān)聯(lián)算法，不僅關(guān)聯(lián)準(zhǔn)確率更高，而且能適用于多種軌道類型的航跡關(guān)聯(lián)。利用文獻(xiàn)[8]中的空間目標(biāo)同步關(guān)聯(lián)方法及多星敏感器聯(lián)合定位算法，將僅測(cè)角數(shù)據(jù)轉(zhuǎn)換成觀測(cè)目標(biāo)的空間坐標(biāo)，并假設(shè)新舊航跡關(guān)聯(lián)的所有情況，從新舊航跡中各取觀測(cè)點(diǎn)作為邊值，求解假設(shè)邊值條件下的目標(biāo)軌道，再以馬氏距離衡量假設(shè)條件下的軌道與實(shí)際觀測(cè)的相似程度，最終從可能關(guān)聯(lián)的閾值中選擇最優(yōu)關(guān)聯(lián)結(jié)果。

1 基于假設(shè)邊值的空間目標(biāo)短弧關(guān)聯(lián)算法

將間隔一定時(shí)長(zhǎng)的航跡片段進(jìn)行關(guān)聯(lián)，先觀測(cè)的航跡定義為舊航跡，后觀測(cè)的航跡定義為新航跡。算法步驟如下：

(1) 獲取m條舊航跡與n條新航跡在J2000坐標(biāo)系下的位置坐標(biāo)。

(2) 構(gòu)造m×n的矩陣，其中元素代表以對(duì)應(yīng)舊航跡一點(diǎn)為起點(diǎn)、新航跡一點(diǎn)為終點(diǎn)作為邊界確定的軌道。

(3) 計(jì)算基于假設(shè)邊值確定的軌道與相應(yīng)新舊航跡觀測(cè)值之間的馬氏距離。

(4) 選擇合適的閾值，小于閾值則接受關(guān)聯(lián)假設(shè)，相應(yīng)新舊航跡進(jìn)行預(yù)關(guān)聯(lián)；大于閾值則拒絕假設(shè)，相應(yīng)新舊航跡不關(guān)聯(lián)。

(5) 進(jìn)行關(guān)聯(lián)多義性處理，僅選擇相似度最高的航跡組合關(guān)聯(lián)，保證每條航跡最多與一條其他航跡關(guān)聯(lián)。

上述步驟涉及空間目標(biāo)的同步關(guān)聯(lián)、多星敏感器協(xié)同定位、蘭勃特定軌問(wèn)題求解、基于馬氏距離與卡方檢驗(yàn)的關(guān)聯(lián)判定，基本原理如下。

1.1 基于對(duì)極幾何的空間目標(biāo)同步關(guān)聯(lián)方法

在某一時(shí)刻，兩臺(tái)及以上星敏感器的視線自然交匯時(shí)，相當(dāng)于對(duì)重疊視野內(nèi)的目標(biāo)進(jìn)行多角度的觀測(cè)。由于空間目標(biāo)距離星敏感器達(dá)數(shù)萬(wàn)公里，因此星圖上的空間目標(biāo)成像與恒星類似，為不具備細(xì)節(jié)特征的亮點(diǎn)。對(duì)極幾何描述的是兩視圖內(nèi)在的射影關(guān)系。當(dāng)目標(biāo)較遠(yuǎn)時(shí)，將目標(biāo)抽象為一點(diǎn)，該點(diǎn)在兩個(gè)不同視角下像的坐標(biāo)存在約束關(guān)系[8]：

(1)

式(1)為對(duì)極幾何約束，p1和p2代表空間目標(biāo)在星圖上的像素坐標(biāo)，第三維補(bǔ)1占位。3階方陣F稱為基礎(chǔ)矩陣：

(2)

(3)

F可根據(jù)相機(jī)標(biāo)定原理求解，如式(2)所示。M1，M2分別代表星敏感器相機(jī)的內(nèi)參矩陣，由式(3)求解。R，S分別代表兩臺(tái)星敏感器的旋轉(zhuǎn)和平移矩陣。星敏感器的相機(jī)參數(shù)已知，星敏感器平臺(tái)定位誤差在百米內(nèi)，測(cè)角誤差在2″內(nèi)，因此每一時(shí)刻兩臺(tái)星敏感器間基礎(chǔ)矩陣可求解，每一時(shí)刻兩星敏感器拍攝空間目標(biāo)是否關(guān)聯(lián)可判定。

式(3)中，fovx×fovy代表相機(jī)角度，Nx×Ny代表照片分辨率，f代表相機(jī)焦距，dx、dy代表像素的長(zhǎng)度和寬度，u0、v0為主點(diǎn)像素坐標(biāo)。上述變量均已知。

由于存在星圖噪聲、星敏感器抖動(dòng)、測(cè)角測(cè)距誤差，關(guān)聯(lián)坐標(biāo)代入式(1)后結(jié)果并不嚴(yán)格為零。設(shè)定關(guān)聯(lián)閾值ε，某一時(shí)刻坐標(biāo)代入式(1)后結(jié)果小于閾值的目標(biāo)判定為關(guān)聯(lián)。重復(fù)上述過(guò)程，最終整理出所有時(shí)刻下，所有空間目標(biāo)的關(guān)聯(lián)結(jié)果[8]。

1.2 多星敏感器協(xié)同定位求解

當(dāng)同一時(shí)刻多星敏感器下的空間目標(biāo)關(guān)聯(lián)問(wèn)題得到解決時(shí)，利用空間目標(biāo)在同一時(shí)刻的多視角觀測(cè)，根據(jù)多目視覺(jué)原理可求解空間目標(biāo)的具體位置。本文空間目標(biāo)的坐標(biāo)在J2000坐標(biāo)系中描述。J2000是經(jīng)典的地心慣性坐標(biāo)系，其X軸指向平春分點(diǎn)，Z軸指向北天極。空間目標(biāo)位置的確定采用一種基于最小二乘的多星敏感器協(xié)同定位方法[8]。

(4)

方向向量與赤經(jīng)赤緯轉(zhuǎn)換關(guān)系為

(5)

(6)

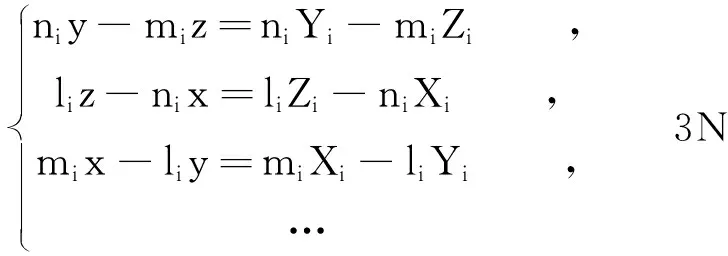
(7)

為求解未知量r(x，y，z)，將其寫(xiě)成線性方程組的形式，為

A·X=b，

(8)

其中，

上述3N個(gè)方程中2N個(gè)相互獨(dú)立。求解3個(gè)未知量，最少需兩個(gè)星敏感器觀測(cè)才可求解。當(dāng)N>2時(shí)，其解為

X=(ATA)-1ATb。

(9)

1.3 基于假設(shè)邊界的蘭勃特問(wèn)題求解

經(jīng)上述過(guò)程，待關(guān)聯(lián)空間目標(biāo)的觀測(cè)數(shù)據(jù)轉(zhuǎn)換成了J2000坐標(biāo)系下的坐標(biāo)，且待關(guān)聯(lián)航跡的間隔時(shí)間已知。這是一個(gè)典型的蘭勃特問(wèn)題，即當(dāng)已知空間目標(biāo)起點(diǎn)和終點(diǎn)的位置和運(yùn)行時(shí)間時(shí)，可求解起點(diǎn)和終點(diǎn)的運(yùn)行速度，繼而求解空間目標(biāo)的運(yùn)動(dòng)軌道[14]。BATTIN對(duì)此類問(wèn)題進(jìn)行了充分的研究。BATTIN法是求解蘭勃特邊界問(wèn)題的經(jīng)典解法。

圖2 蘭勃特問(wèn)題幾何關(guān)系

圖3 蘭勃特問(wèn)題轉(zhuǎn)換形式

由圖2所示，蘭勃特問(wèn)題中若起始位置ri、終點(diǎn)位置rf確定，飛行時(shí)間是轉(zhuǎn)移軌道半長(zhǎng)軸a的函數(shù)，即

t=f(a，ri，rf) 。

(10)

根據(jù)蘭勃特問(wèn)題理論，若轉(zhuǎn)移軌道開(kāi)始和結(jié)束位置p1，p2固定，則|ri|+|rf|和半長(zhǎng)軸在運(yùn)行中不變，轉(zhuǎn)移軌道初始焦點(diǎn)和虛焦點(diǎn)可以不受飛行時(shí)間約束，轉(zhuǎn)移軌道形狀不變。

如圖3所示，轉(zhuǎn)換后軌道p2點(diǎn)的真近點(diǎn)角為

(11)

其中，θ為圖2中ri與rf之間的夾角。

飛行時(shí)間函數(shù)為

(12)

其中，偏心率為e；μ=398 600.44 m3/s2，代表地球引力常數(shù)。根據(jù)式(12)，可推導(dǎo)出式(13)～(15)：

(13)

(14)

(15)

可通過(guò)迭代方法求解y[15]。最終軌道起始位置的速度vi為

(16)

中間量p為

(17)

1.4 基于馬氏距離與卡方檢驗(yàn)的中斷航跡關(guān)聯(lián)判定

從舊航跡取一點(diǎn)作為起點(diǎn)，從新航跡取一點(diǎn)作為終點(diǎn)。若有m條舊航跡，n條新航跡，則共有mn種可能的運(yùn)動(dòng)情況；若舊航跡i與新航跡j屬于同一目標(biāo)，則在相同觀測(cè)時(shí)刻，軌道上目標(biāo)的理論位置必與舊航跡i和新航跡j的觀測(cè)值接近，航跡的相似度利用馬氏距離衡量[16]。在觀測(cè)時(shí)刻k，舊航跡i和新航跡j關(guān)聯(lián)理論值與觀測(cè)值的馬氏距離為

(18)

其中，Σ為協(xié)方差矩陣，可根據(jù)星敏感器的誤差獲得。

求出N個(gè)觀測(cè)時(shí)刻的馬氏距離，并求均值：

(19)

由于可能存在某條新航跡無(wú)法與任意一條舊航跡關(guān)聯(lián)的情況，因此設(shè)置門(mén)限d。當(dāng)新舊航跡平均馬氏距離大于d，則判定為相應(yīng)新舊航跡不關(guān)聯(lián)。門(mén)限d的選取參考χ2檢驗(yàn)法[17]。空間目標(biāo)坐標(biāo)為三維，應(yīng)服從三自由度的卡方分布。顯著性水平α=0.01，門(mén)限d=11.344。

對(duì)任一條航跡，從其滿足門(mén)限d的所有候選關(guān)聯(lián)航跡中選擇平均馬氏距離最小的航跡判定為關(guān)聯(lián)，并保證每條航跡至多有一條關(guān)聯(lián)航跡。

2 仿真校驗(yàn)

2.1 多星敏感器協(xié)同定位精度仿真

利用衛(wèi)星工具包(Satellite Tool Kit，STK)平臺(tái)構(gòu)建觀測(cè)模型。觀測(cè)平臺(tái)位于太陽(yáng)同步軌道，軌道參數(shù)參考美國(guó)優(yōu)思科學(xué)家聯(lián)盟的觀測(cè)數(shù)據(jù)。觀測(cè)平臺(tái)的軌道傾角范圍為96.8°～98.5°，軌道半長(zhǎng)軸為6 778.14 km，偏心率為0，每個(gè)平臺(tái)正交安裝兩臺(tái)視場(chǎng)為2°×2°的星敏感器。觀測(cè)目標(biāo)位于軌道半長(zhǎng)軸為42 126.1～42 805.9 km的地球同步軌道，軌道傾角為0°～2°。共進(jìn)行了200次地球同步軌道目標(biāo)的協(xié)同定位，計(jì)算了空間目標(biāo)定位坐標(biāo)與實(shí)際坐標(biāo)的誤差。為模擬任務(wù)中星敏感器定姿誤差及平臺(tái)自身的位置誤差，對(duì)測(cè)角、測(cè)距數(shù)據(jù)加入噪聲。仿真中設(shè)置了3種噪聲水平，(a″，b)意味著對(duì)星敏感器的測(cè)角數(shù)據(jù)加入均值為零、標(biāo)準(zhǔn)差為a″的高斯白噪聲，對(duì)星敏感器的位置矢量加入均值為零、標(biāo)準(zhǔn)差為b的高斯白噪聲。圖4反映了200次計(jì)算中空間目標(biāo)在X，Y，Z軸的定位誤差情況。

(a) X軸誤差

(b) Y軸誤差

(c) Z軸誤差

三軸定位誤差的標(biāo)準(zhǔn)差如表1所示。當(dāng)噪聲(1″，100 m)增大到(2″，100 m)時(shí)，定位誤差改變了0.922 3 km；當(dāng)噪聲(2″，100 m)時(shí)增大到(2″，1 000 m)時(shí)，定位誤差僅改變了0.794 4 km。測(cè)角誤差多1″，就會(huì)對(duì)定位結(jié)果產(chǎn)生明顯的影響。可見(jiàn)協(xié)同定位算法對(duì)測(cè)角誤差更為敏感。星敏感器測(cè)角越準(zhǔn)，定位精度越高，后續(xù)關(guān)聯(lián)效果將越好。

表1 三軸定位誤差的標(biāo)準(zhǔn)差

2.2 空間目標(biāo)短弧關(guān)聯(lián)仿真

采用實(shí)測(cè)數(shù)據(jù)與仿真相結(jié)合的研究方法，將真實(shí)的地球同步軌道數(shù)據(jù)導(dǎo)入衛(wèi)星工具包。軌道半長(zhǎng)軸為42 126.1～42 805.9 km，軌道傾角為0°～2°。圖5為2019年12月1日0時(shí)在軌533個(gè)地球同步軌道目標(biāo)在J2000坐標(biāo)系下的分布密度圖，縱軸代表1°×1°區(qū)域內(nèi)空間目標(biāo)個(gè)數(shù)。可知目標(biāo)在中國(guó)、俄羅斯、美國(guó)的上空較為密集。據(jù)統(tǒng)計(jì)，大多數(shù)地球同步軌道目標(biāo)分布的赤道緯度接近于0°，且都為近圓軌道，最大偏心率為0.075，其中80%目標(biāo)的軌道傾角小于1°。

仿真中觀測(cè)平臺(tái)建立在傾角范圍為96.8°～98.5°、軌道半長(zhǎng)軸為6778.14 km、偏心率為0的30個(gè)太陽(yáng)同步軌道上，每個(gè)平臺(tái)正交安裝兩臺(tái)視場(chǎng)為2°×2°的星敏感器，組成空間目標(biāo)監(jiān)視網(wǎng)。利用衛(wèi)星工具包平臺(tái)獲取連續(xù)時(shí)刻及對(duì)應(yīng)時(shí)刻坐標(biāo)作為航跡數(shù)據(jù)。根據(jù)節(jié)2.1的結(jié)果對(duì)航跡坐標(biāo)添加噪聲，每組噪聲下共進(jìn)行了500次的關(guān)聯(lián)仿真。定義觀測(cè)時(shí)長(zhǎng)180 s以下的弧段為短弧。為著重突出短弧關(guān)聯(lián)效果，選擇觀測(cè)時(shí)長(zhǎng)為50～120 s的航跡數(shù)據(jù)進(jìn)行關(guān)聯(lián)。一般空間目標(biāo)的重訪時(shí)間為20～50 min，可關(guān)聯(lián)的航跡間隔時(shí)間越長(zhǎng)，數(shù)據(jù)的利用率越高。仿真中最大間隔時(shí)間為10 h，可滿足絕大部分的中斷航跡關(guān)聯(lián)需求。在雙核Intel 2.5 GHz的MacBook pro上，采用Matlab2018a版本進(jìn)行航跡關(guān)聯(lián)仿真。

關(guān)聯(lián)性能由真正類(True Positive，TP)、真負(fù)類(True Negative，TN)、假正類(False Positive，F(xiàn)P)、假負(fù)類(False Negative，F(xiàn)N)4個(gè)量來(lái)描述，TP指正確關(guān)聯(lián)相同目標(biāo)，TN指正確拒絕不同目標(biāo)，F(xiàn)P為誤關(guān)聯(lián)不同目標(biāo)，F(xiàn)N指漏關(guān)聯(lián)相同目標(biāo)。圖6所示為基于假設(shè)邊值的關(guān)聯(lián)算法在不同噪聲條件下的關(guān)聯(lián)正確率。隨著間隔時(shí)間增加，關(guān)聯(lián)準(zhǔn)確率呈下降趨勢(shì)。根據(jù)現(xiàn)有星敏感器的性能，測(cè)角誤差為2″、位置誤差為100 m的噪聲更符合工程應(yīng)用實(shí)際。參考三角記號(hào)折線，航跡間隔10 h，關(guān)聯(lián)準(zhǔn)確率達(dá)95%。表2展示了在此噪聲條件下，不同間隔時(shí)間下的具體關(guān)聯(lián)結(jié)果。

圖5 地球同步轉(zhuǎn)道目標(biāo)分布密度圖

圖6 關(guān)聯(lián)準(zhǔn)確率與間隔時(shí)間的關(guān)系

表2 關(guān)聯(lián)結(jié)果統(tǒng)計(jì)

仿真中的關(guān)聯(lián)門(mén)限值d取11.344。若新舊航跡平均馬氏距離大于d，則判定為不相關(guān)航跡。門(mén)限值與關(guān)聯(lián)同一目標(biāo)的概率有關(guān)[18]。門(mén)限值取得過(guò)小，會(huì)將同一目標(biāo)拒絕，造成漏關(guān)聯(lián)；門(mén)限值取得過(guò)大，則可能將不同的目標(biāo)誤判為關(guān)聯(lián)。關(guān)聯(lián)同一目標(biāo)概率隨門(mén)限取值變化如圖7所示，曲線先增大后緩慢減小。由于來(lái)自于同一目標(biāo)觀測(cè)數(shù)據(jù)與預(yù)測(cè)數(shù)據(jù)的馬氏距離往往比來(lái)自不同目標(biāo)的馬氏距離小，因此達(dá)到最大關(guān)聯(lián)概率后的下降趨勢(shì)相較于上升趨勢(shì)平緩得多。

圖8為目標(biāo)關(guān)聯(lián)的可視化展示。圖中3個(gè)方塊代表3個(gè)觀測(cè)時(shí)刻，依次間隔為1 h，觀測(cè)目標(biāo)為地球同步軌道目標(biāo)，成功關(guān)聯(lián)的目標(biāo)用相同標(biāo)記表示，可知共有4個(gè)地球同步軌道目標(biāo)。地球同步軌道目標(biāo)繞地心運(yùn)動(dòng)的角速度約15°/h，與圖8中地球同步軌道運(yùn)動(dòng)狀態(tài)相吻合。

圖7 關(guān)聯(lián)概率與閾值的關(guān)系

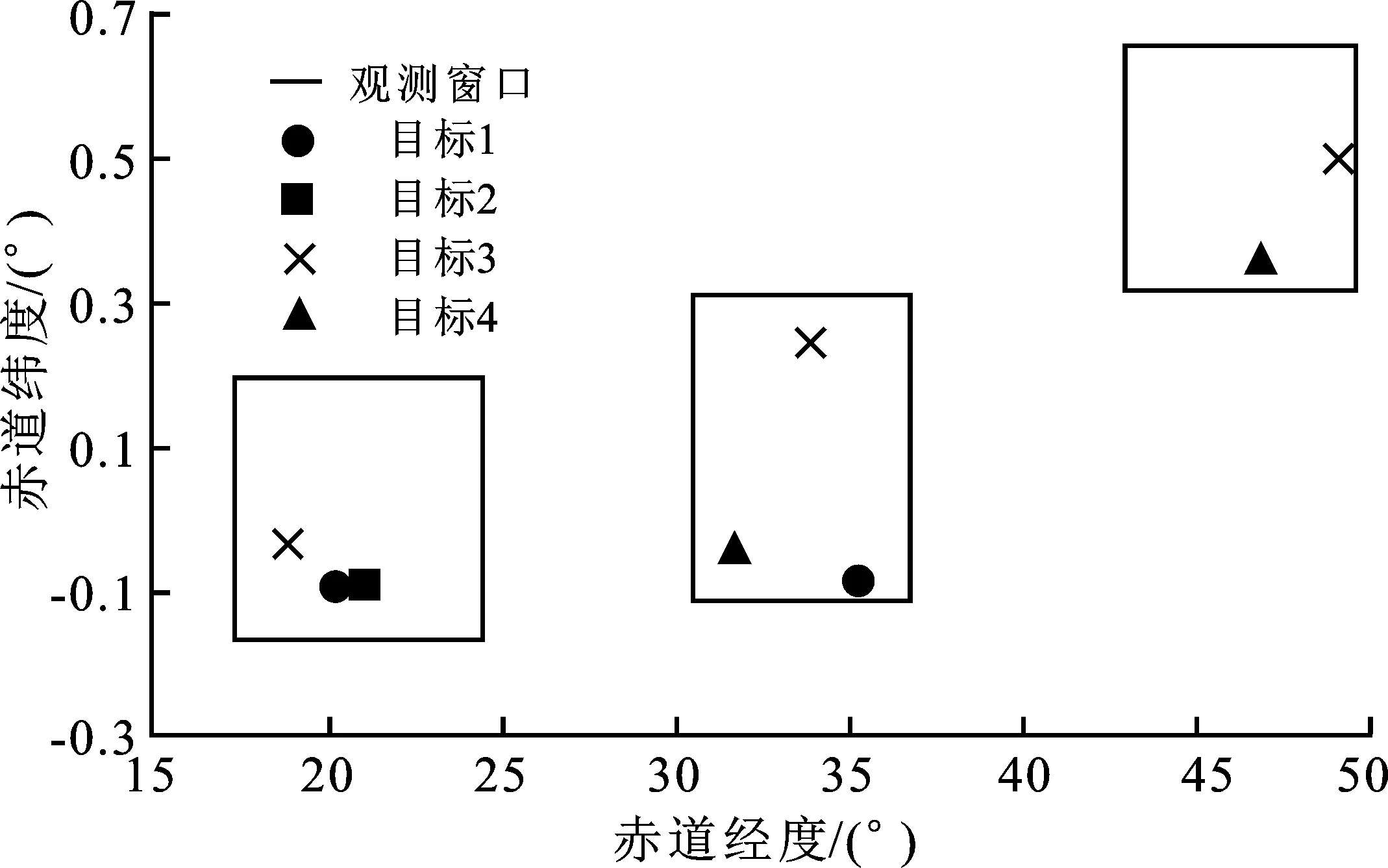
圖8 關(guān)聯(lián)結(jié)果示例

3 短弧關(guān)聯(lián)算法對(duì)比

為測(cè)試基于假設(shè)邊值的航跡關(guān)聯(lián)算法解決短弧關(guān)聯(lián)問(wèn)題的性能，通過(guò)仿真從關(guān)聯(lián)準(zhǔn)確率、運(yùn)行時(shí)間兩個(gè)角度，與基于正弦擬合和基于容許域的短弧關(guān)聯(lián)算法進(jìn)行對(duì)比。容許域算法通過(guò)將目標(biāo)的軌道限制在測(cè)量斜距與斜距變化率的平面的一定范圍內(nèi)，以尋找和觀測(cè)值誤差最小的軌道作為初軌，根據(jù)目標(biāo)的半長(zhǎng)軸、軌道傾角等特點(diǎn)可以進(jìn)一步縮小約束范圍。基于正弦擬合的關(guān)聯(lián)算法利用同一軌道的赤道經(jīng)緯度的變化，近似正弦分布的規(guī)律，區(qū)分軌道傾角不同的軌道。仿真中添加噪聲為(2″，100 m)的高斯白噪聲，仿真中的關(guān)聯(lián)閾值d取11.344。3種算法分別對(duì)不同間隔時(shí)間進(jìn)行100次仿真，統(tǒng)計(jì)關(guān)聯(lián)準(zhǔn)確率如圖9所示，并在上述仿真過(guò)程中對(duì)5、10、30、60個(gè)目標(biāo)同時(shí)關(guān)聯(lián)的平均運(yùn)行時(shí)間進(jìn)行計(jì)算，如圖10所示。

基于假設(shè)邊值的短弧關(guān)聯(lián)算法與基于正弦擬合的短弧關(guān)聯(lián)算法[10]利用了多星敏感器同步關(guān)聯(lián)結(jié)果，融合了多星敏感器的同步觀測(cè)數(shù)據(jù)，而容許域方法針對(duì)單平臺(tái)僅測(cè)角數(shù)據(jù)，因此基于容許域方法的關(guān)聯(lián)準(zhǔn)確率最低，且容許域約束相對(duì)寬松。基于容許域方法對(duì)每個(gè)觀測(cè)目標(biāo)都需要在容許域內(nèi)尋找最優(yōu)初軌，再外推到下一時(shí)刻與后一時(shí)刻的目標(biāo)進(jìn)行關(guān)聯(lián)，過(guò)程復(fù)雜，關(guān)聯(lián)時(shí)間也是最長(zhǎng)的。基于正弦擬合的空間目標(biāo)關(guān)聯(lián)算法[10]可以較為便捷地區(qū)分傾角不同的軌道，對(duì)于同軌道不同相位或僅軌道高度不同的空間目標(biāo)需增加額外約束條件，因此難以適應(yīng)多種軌道類型的目標(biāo)關(guān)聯(lián)，并且隨關(guān)聯(lián)間隔時(shí)間增加，關(guān)聯(lián)準(zhǔn)確率下降明顯；由于無(wú)須進(jìn)行軌道確定及軌道外推，運(yùn)算最快。基于假設(shè)邊值關(guān)聯(lián)算法的運(yùn)算時(shí)間略高于基于正弦擬合關(guān)聯(lián)算法，但關(guān)聯(lián)準(zhǔn)確率在3種算法中最高；從仿真結(jié)果看，當(dāng)航跡間隔在10 h內(nèi)時(shí)，進(jìn)行關(guān)聯(lián)的準(zhǔn)確率均比較高。

圖9 準(zhǔn)確率的對(duì)比

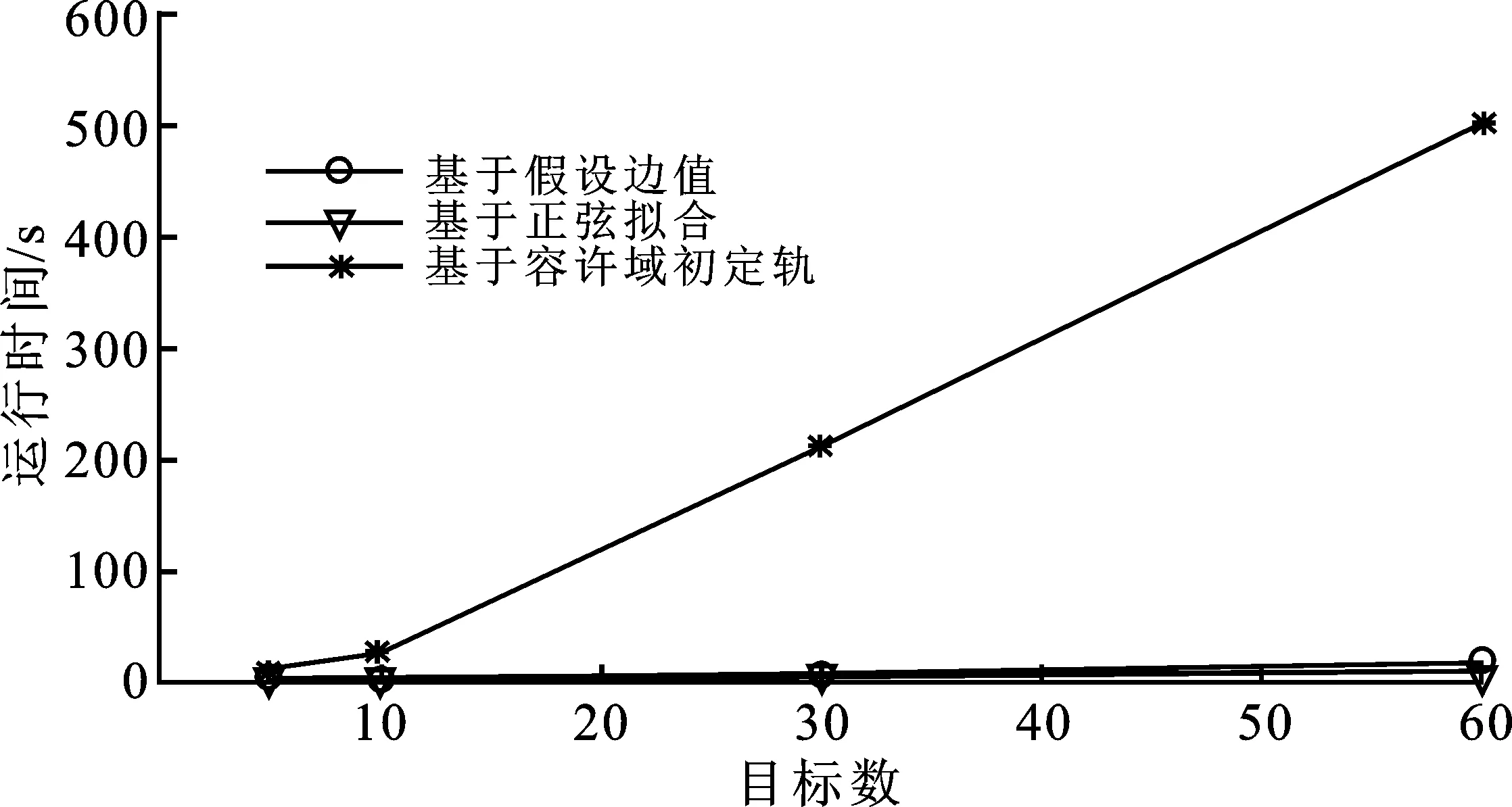
圖10 運(yùn)行時(shí)間對(duì)比

4 結(jié) 論

在多星敏感器觀測(cè)的空間目標(biāo)同步關(guān)聯(lián)結(jié)果基礎(chǔ)上，使用最小二乘方法將相同時(shí)刻多星敏感器觀測(cè)的測(cè)角數(shù)據(jù)融合，解算出各空間目標(biāo)在J2000坐標(biāo)系下的坐標(biāo)。當(dāng)星敏感器位置誤差的標(biāo)準(zhǔn)差為100 m、測(cè)角數(shù)據(jù)誤差的標(biāo)準(zhǔn)差為2″時(shí)，空間目標(biāo)定位誤差的標(biāo)準(zhǔn)差為1.977 1 km，足以滿足后續(xù)關(guān)聯(lián)步驟的精度需求。基于假設(shè)邊值和基于正弦擬合關(guān)聯(lián)算法的應(yīng)用前提是需至少兩臺(tái)星敏感器對(duì)空間目標(biāo)進(jìn)行觀測(cè)，根據(jù)文獻(xiàn)[5]相關(guān)研究，90%同步軌道帶目標(biāo)可被兩臺(tái)以上星敏感器同步觀測(cè)。

從新舊航跡中各取一點(diǎn)作為邊界，建立所有假設(shè)邊界的集合，計(jì)算出所有假設(shè)邊界條件下空間目標(biāo)軌道的理論值，并利用馬氏距離與卡方檢驗(yàn)作為航跡關(guān)聯(lián)準(zhǔn)則。經(jīng)仿真驗(yàn)證，當(dāng)噪聲為(2″，100 m)的高斯白噪聲時(shí)，對(duì)兩組間隔10 h航跡關(guān)聯(lián)的準(zhǔn)確率可達(dá)95%。與其他短弧關(guān)聯(lián)算法相比，基于假設(shè)邊值的航跡關(guān)聯(lián)算法在關(guān)聯(lián)準(zhǔn)確率上具有明顯優(yōu)勢(shì)，同時(shí)保持了較快的運(yùn)行速度。

仿真中采用的最短觀測(cè)僅50 s，無(wú)法用常規(guī)軌道確定方法確定初始軌道，符合短弧定義。基于假設(shè)邊值的航跡關(guān)聯(lián)算法實(shí)現(xiàn)了因觀測(cè)弧段過(guò)短無(wú)法確定初軌的航跡關(guān)聯(lián)問(wèn)題，而且算法不僅局限于短弧關(guān)聯(lián)，對(duì)一般的航跡關(guān)聯(lián)問(wèn)題同樣適用。若未來(lái)星間鏈路能夠?qū)崿F(xiàn)衛(wèi)星間數(shù)據(jù)共享，則空間目標(biāo)關(guān)聯(lián)的過(guò)程可在衛(wèi)星上實(shí)現(xiàn)，無(wú)需再將大量數(shù)據(jù)下傳回地面。由于衛(wèi)星的運(yùn)算資源是有限的，因此算法不宜過(guò)于復(fù)雜。在3種短弧關(guān)聯(lián)算法中，基于假設(shè)邊值的航跡關(guān)聯(lián)算法更有利于實(shí)現(xiàn)星上數(shù)據(jù)處理。

考慮到各平臺(tái)的實(shí)際測(cè)量誤差可能有所不同，后續(xù)將對(duì)不同平臺(tái)的觀測(cè)誤差賦予相應(yīng)的權(quán)重，進(jìn)一步提高空間目標(biāo)的定位精度。目前，工程中星敏感器僅作為姿態(tài)傳感器應(yīng)用，通過(guò)實(shí)測(cè)數(shù)據(jù)與仿真軟件相結(jié)合的手段，可為后續(xù)工程應(yīng)用提供借鑒。隨著新型小視場(chǎng)、高極限星等星敏感器的研發(fā)，后續(xù)將在真實(shí)星圖下進(jìn)一步進(jìn)行空間目標(biāo)提取研究。