3腔道仿生軟體爬行機器人設計

霍前俊， 劉 勝， 張遠飛， 陳國慶， 毛 蔚

(上海工程技術大學 機械與汽車工程學院， 上海 201620)

由柔性材料[1]制成的軟體機器人，可在較大的范圍內任意改變自身形狀和尺寸。與傳統剛性機器人相比，柔性材料賦予了軟體機器人更加優越的特性[2]，如改進機械的魯棒性、簡化了機械的結構與控制[3],以及更加安全的人機互交功能。這些優異的特性使得軟體機器人在醫療、加工制造、探測及救援等[4-6]眾多領域都有廣闊的應用前景。

近年來，軟體機器人技術在國內外得到了巨大的發展，其中仿生型軟體機器人因為其通用性和應用范圍廣的特點，得到眾多學者的廣泛關注。Rus研究團隊設計了一款仿蛇形氣動軟機器人[7-8]，基于蛇形蜿蜒運動的數學關系，建立了軟體機器人蛇形步態算法。Nemitz帶領的團隊基于聲圈驅動研制了一款軟體模塊化機器人[9]，實現了機器人仿蠕蟲運動。此外，Renda和SADATI等利用繩索驅動設計了一款軟體操作臂機器人[10-11]，建立了多段式軟體操作臂的力學控制模型。然而，前人研究多自由度軟體機器人多基于復雜的多模塊結構和繁瑣的控制系統。如何基于單個驅動器、簡單的控制系統設計出更靈活的且力學性能更加有效的仿生軟體機器人的方法前人涉及相對較少。

課題組設計了一款3腔道外波紋式軟體驅動器，基于Yeoh模型構建氣壓與驅動器彎曲步幅的非線性數學預測模型。結合有限元仿真和樣機試驗驗證預測模型的有效性。同時將3腔道軟體驅動器與卡腳相結合研制了一種結構簡潔、靈活性高的仿生軟體爬行機器人。

1 仿生軟體爬行驅動器的結構設計

軟體驅動器是否具有良好的彎曲性能是由驅動器的延展面和約束面共同決定的。為提高軟體驅動器的彎曲性能，將驅動器的延展面設計為波紋結構，其驅動器外壁直徑相等，驅動器結構如圖1所示。

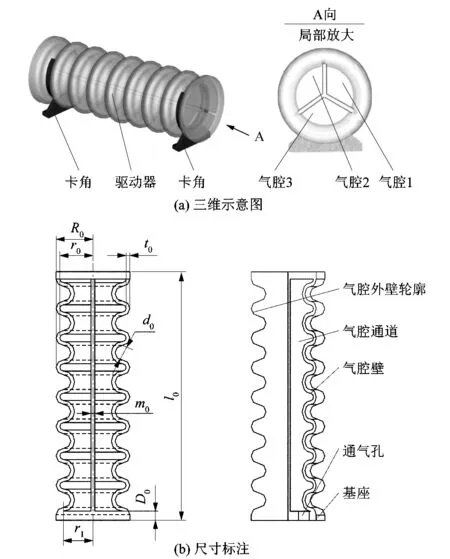
圖1 軟體爬行的結構示意圖Figure 1 Structural diagram of soft robot crawling

借鑒所研究的多腔式軟體驅動器結構，將波紋管氣腔劃分為3個等體積的扇形腔室，并對3個腔室進行命名如圖1(a)，驅動器在3個氣腔的相互作用下可實現周向360°彎曲變形。該軟體驅動器結構簡單、反應速度快、彎曲方向靈活，經過多次的仿真與實驗，并結合驅動器的結構特性確定了軟體驅動器的結構尺寸，如表1所示。

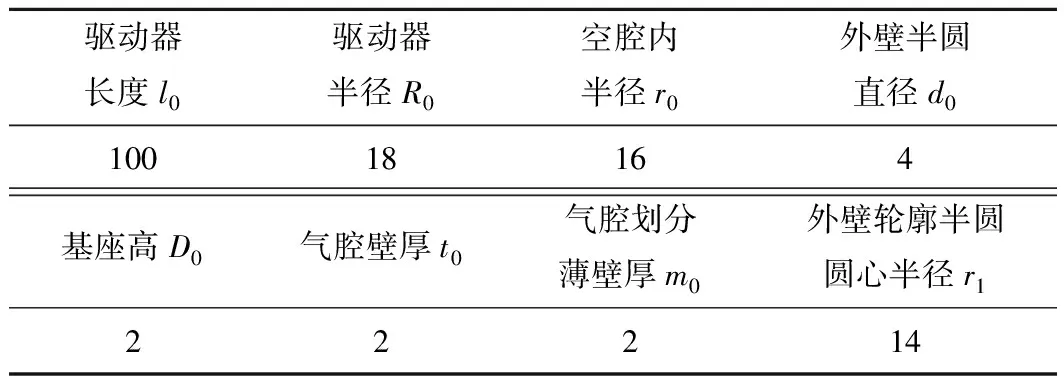
表1 軟體驅動器設計參數Table 1 Software driver design parameters mm

2 超彈性材料本構模型

軟體驅動器的材料均具有非線性力學特性。在力的作用下，驅動器本身可延展數倍于自身長度。當撤銷外力時，又會恢復到原有的狀態。國內外學者提出了許多超彈性材料的本構模型，例如Mooney-Rivlin模型、Yeoh模型和Valanis-Landel應變能函數等。為了簡化數學預測模型，選擇Yeoh模型作為超彈性材料的應變能密度函數。

超彈性軟體硅膠材料具有各向同性且不可壓縮性，故可得應變能密度函數的通用式：

W=W(I1,I2,I3)。

(1)

硅膠材料具有不可壓縮性，即其式中I1=1，式中I1,I2和I3為變形張量不變量。其公式如下：

(2)

(3)

(4)

式中：λ1，λ2和λ3分別為軸向拉伸比、徑向拉伸比和周向拉伸比。

由上文可知選用Yeoh模型建立氣壓-彎曲數學模型，其應變能密度函數為：

(5)

式中：N，Ci和dk分別為材料常數；對于不可壓縮硅膠材料J=1。

二參數是常用的經典形式，當N=2時即為二參數形式:

W=C1(I1-3)+C2(I1-3)2。

(6)

假設徑向拉伸比λ2=1，由公式(4)可得:

(7)

經過化簡可得：

(8)

3 非線性建模

驅動器在氣壓的作用下彎曲，在此過程中未受其他外力作用。根據虛功原理可認為氣壓做的功完全消耗于驅動器的變形所需要的功，其表達式為：

pdVa=VrdW。

(9)

式中：Va為變形后氣腔體積,Vr為變形后硅膠材料的體積，p為氣壓。

由于硅膠材料的不可壓縮性，Vr可視為未變形前的硅膠材料體積以便于計算。式(9)2邊對彎曲角度θ進行求導可得:

(10)

驅動器的各個氣囊幾何特征完全相似，可將多個相同的氣囊內幾何體積視為圖2所示圖形繞Y軸旋轉180°所得。同時將氣囊分成V1和V22部分，其平面示意圖如圖2所示。

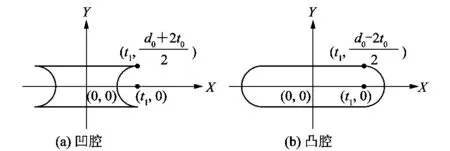
圖2 驅動器氣囊平結構面示意圖Figure 2 Schematic diagram of flat structure of driver airbag

(11)

(12)

軟體驅動器的分隔腔室的薄壁體積V3的表達式為：

(13)

式中m為軟體驅動器劃分氣腔的個數。

由式(11)～式(13)可得變形后氣腔體積Va的近似表達式：

(14)

為了便于求出驅動器硅膠材料的體積，先計算出整個驅動器的體積 (氣腔體積加硅膠材料體積)。同理將驅動器劃分成2個部分：8個內凹部分和7外凸部分。由于驅動器外壁輪廓的半圓直徑相等，即驅動器的體積V4表達式為：

(15)

由式(11)～(13)和式(15)可得硅膠材料體積Vr的表達式：

(16)

由公式(10)變形可得氣壓和彎曲角度之間的數學關系：

(17)

根據式(16)、式(8)和式(14)可知公式(17)中僅含有未知量p和θ2個未知量，即明確壓強和驅動器彎曲角度之間的數學關系：

θ=θ(p)。

(18)

驅動器在氣壓的作用下彎曲形變，其彎曲形變可近似視為等直徑的圓弧，如圖3所示。

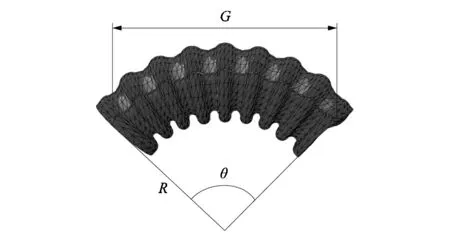
圖3 驅動器拱起時結構參數Figure 3 Structure parameter of driver arching

已知驅動器原長為l0，如圖3可知步幅G、彎曲半徑R與彎曲角度θ的數學關系：

(19)

(20)

由式(18)～(20)可知壓強p和驅動器步幅G之間的非線性關系：

(21)

4 樣機實驗與仿真

4.1 驅動器的彎曲實驗

在三維軟件中建立3腔道仿生軟體爬行幾何模型，導入Abaqus中，并設置材料參數C1=0.11 MPa，C2=0.02 MPa。為了使軟體爬行機器人獲得最大的步幅G，各個氣腔在氣壓的作用下相互協調控制驅動器的彎曲程度和變形方向。分別對驅動器的幾何模型和實物樣機進行單腔道、雙腔道彎曲試驗。如圖4所示，從上到下對應的氣壓分別為0.005，0.010，0.015，0.020，0.025和0.030 MPa。圖中深色為模型，白色為實物樣機。

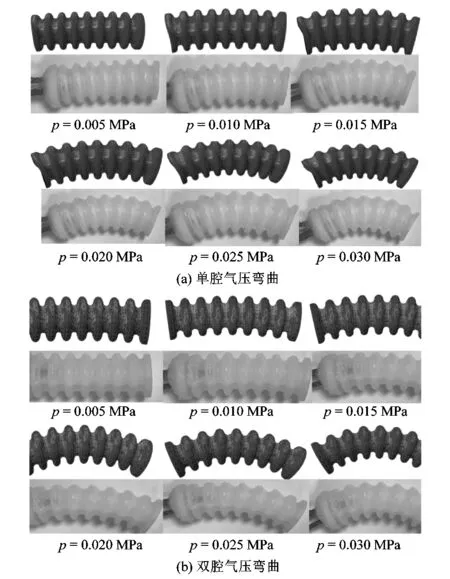
圖4 仿真與實驗對比圖Figure 4 Comparison of simulation and experiment

為驗證仿真與預測模型的準確性，根據仿真、實驗和預測結果繪制了單腔道氣壓、雙腔道氣壓下驅動器充入氣壓與步幅值曲線，如圖5所示。

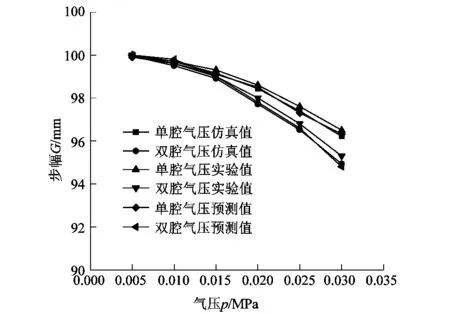
圖5 不同氣壓、氣腔下驅動器步幅值Figure 5 Step value of driver under different air pressure and air cavity

如圖5所示，隨著氣壓的增大驅動器步幅逐漸減小、彎曲程度加大。與單腔氣壓相比，通入相同氣壓條件下雙腔氣壓使驅動器彎曲程度更大。因而選擇雙腔同時通入氣壓，為爬行機器人提供動力。同時驅動器的實際測量值和理論模型值、有限元分析值有一定的誤差，但整體的趨勢基本相同。

4.2 驅動器的爬行實驗

為驗證3腔道仿生軟體爬行機器人的運動能力，對爬行機器人的運動姿態進行仿真與實驗，得出了爬行機器人可以模仿自然界環節蠕蟲的3個基本動作：轉向、前進和抬頭。爬行機器人運動姿態如圖6所示。

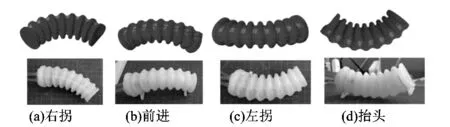
圖6 爬行機器人運動姿態Figure 6 Movement posture of crawling robot

由圖6可知，爬行機器人基本具備環節蠕蟲的運動特性。為驗證爬行機器人的爬行能力，進行了如圖7所示的前進運動試驗。

圖7 爬行機器人前進運動圖Figure 7 Forward motion diagram of crawling robot

如圖7所示，橫線為爬行機器人起始位置，對驅動器氣腔1和氣腔2進行2次沖放氣，爬行機器人向前前進了2 mm。

5 結論

課題組依據仿生學原理，以環節動物的身體結構、運動原理為基礎，以超彈性材料為依托，研究并設計了一款3腔道軟體爬蟲機器人。主要研究工作如下：

1) 將3腔道軟體驅動器和前后卡腳相結合，設計3腔道仿生爬行機器人。

2) 根據機器人一曲一伸周期性運動特性，基于Yeoh模型推導出機器人運動步幅與氣壓的非線性數學預測模型。

3) 進行了有限元仿真和樣機試驗，并將所得數據與預測值進行比較分析，驗證了數學預測模型的有效性。

4) 通過試驗驗證了爬行機器人的前進、轉向和抬頭運行的可行性。

該軟體機器人具有較好的靈活性、更加簡單的結構和良好的力學性能，適用于多種非結構化場景，具有較好的通用性，因此有著重要的研究意義與市場潛力。今后應繼續研究爬行機器人各種仿生運動，并將電氣控制集成到驅動器內部，實現無線控制。