超臨界水對流換熱的寬范圍數據分析及換熱關聯式的建立

蔡文熠，匡　波

超臨界水對流換熱的寬范圍數據分析及換熱關聯式的建立

蔡文熠，匡波

（上海交通大學，上海 200240）

由于超臨界流體在擬臨界區復雜的物性變化，其管內流動的對流換熱模式與亞臨界流體有很大不同。除實驗研究和理論分析外，許多學者建立了用于預測換熱系數的超臨界流體換熱關聯式，但現有的關聯式均不能在寬廣的參數范圍上取得滿意的預測效果。因此，在建立了超臨界水豎直上升流寬范圍換熱實驗數據庫的基礎上，運用機器學習方法分析了影響換熱的典型無量綱數與努塞爾數的關系，建立客觀評價指標，選出適當的關聯形式并建立新的換熱關聯式。換熱關系的非線性分析結果表明，其非線性特征在密度比上的表現最為顯著。結合非線性特征的趨勢和客觀評價指標的對比，在換熱關聯式中引入對數型的密度比項，由此提出寬范圍的超臨界水豎直上升流換熱關聯式，其在數據庫上的預測表現明顯優于現有關聯式。

超臨界水；換熱關聯式；寬范圍換熱實驗數據庫；機器學習

當壓力高于臨界壓力時，流體會失去氣相與液相的分界，這種單相狀態被稱為超臨界。處于超臨界狀態的流體具有良好的傳熱和流動特性，在動力工程領域有廣泛的應用前景。然而，在被稱為擬臨界區的溫度范圍內，超臨界流體的物性會發生劇烈變化，傳統的單相換熱關聯式無法準確預測其換熱系數，這給超臨界流體的工程應用帶來很大困難。

根據現有研究，擬臨界區的流體在徑向和流向上易出現陡峭的密度梯度，從而引發浮力效應和加速效應，對換熱強度產生復雜影響[1]。然而，對于這種影響關系的具體形式還未能給出準確的定量表述，學者們只能嘗試在關聯式中加入物性比、浮力因子、加速因子等修正項并用實驗數據擬合出修正關聯式。一方面大部分修正關聯式都沒有在較寬廣的參數范圍內（尤其是擬臨界區）取得令人滿意的效果，另一方面對于這些修正變量與換熱強度的關系，少有學者利用數據科學的工具進行數據分析和討論，以篩選出重要的修正變量及適合的關聯形式。因此，需要在寬廣參數覆蓋范圍的換熱實驗數據集上進行深入的數據分析，確定應引入關聯的變量組合及恰當的關聯形式，以獲得更好的預測精度。

1　數據庫建立及均衡化處理

本文針對超臨界水管內豎直上升流的換熱實驗工況，從1963—2016年的文獻[2-23]中共搜集到18 079個有效數據樣本。樣本包含管徑、壓力、質量流密度、熱流密度、流體溫度b或焓值b、壁面溫度w這六項原始實驗參數。

由于文獻目的及獲取途徑的不同，原始樣本數在各數據來源間差異很大（最大數據源數據量為5 088，最小源只有77）。樣本量較大的數據源會使模型向它過度“偏移”，而樣本量較小的數據源則容易被模型“忽視”，這對后續建模十分不利。

在樣本量小的數據源上隨機選取樣本視為新樣本加入數據庫，以平衡數據分布，這種方法稱為隨機過采樣。本文中當某數據源樣本量小于最大數據源的四分之一時，需要對該數據源進行一定比例的過采樣，且最大采樣倍數不超過10。經隨機過采樣后，得到規模為26 358的均衡化數據集，后續的建模和評價都將在均衡化數據集上進行。

2　無量綱自變量的篩選

前人基于假設、理論推導或實驗擬合，得到了許多不同類型的無量綱數作為修正因子引入換熱關聯式中，主要包括反映物性變化的因子、反映浮力效應的因子以及反映熱加速效應的因子。一方面，由于關聯式表現不佳，更多變量被引入試圖反映出不同因素對換熱的影響；另一方面，過多的變量容易導致關聯式系數不穩定，模型失真，外推能力變差。這就需要對自變量作得當的篩選，以選取盡可能少但又能充分反映換熱關系特點的自變量。

參考不同學者提出的換熱關聯式及其中因子，挑選出以下9個相對較多學者使用的無量綱數作為待篩自變量（見表1）。

表1　選取的待篩選自變量

最終模型是否包含這些變量，還需要結合數據進行篩選。自變量篩選需要考慮兩方面因素：

（1）該變量對于影響程度的大小，即變量與的關聯度；

（2）變量之間是否存在相關性，內部相關性強的變量組將使模型參數估計值不穩定，影響預測效果。

用Lasso回歸方法可以篩去與目標函數關聯度較低的變量并保留內部相關性弱的變量組[24]。Lasso線性回歸模型的損失函數如下：

表2　各變量在Lasso回歸中的系數估計值

r、r、+、*這4個變量因與模型關聯度不顯著或與保留變量組有較強相關性而被剔除，、、r、p,r、B這5個自變量被保留。

3　換熱關系中的非線性成分分析

3.1　線性模型的評價

使用Lasso回歸保留下來的自變量組及相應系數建立線性模型，并引入下列指標來評價模型預測效果：

其中為平均相對誤差，2為決定系數。另外，還定義10、20、30分別表示相對誤差在10%、20%、30%以下的數據比例。在評價中采用交叉驗證的思想，隨機選取均衡化數據集中的70%樣本作為訓練集，余下的30%作為測試集，模型在訓練集上得到其參數，并在測試集上評估效果。這樣確保建立好的模型從未“見過”評價它所用的樣本，有效防止過擬合的模型獲得較高評價。

線性模型的評價指標如表3所示，其在測試集上的詳細表現如圖1所示。經過變量篩選后的線性模型已經能在一定程度上預測，但從圖中看，仍有較多樣本的預測相對誤差超過30%，且一些樣本的誤差非常大。這說明線性模型不能較充分地表示換熱關系。

表3　Lasso線性回歸模型的評價

圖1　Lasso線性回歸模型的預測效果

3.2　非線性成分說明和驗證

為進一步分析各變量在不同參數子空間上對換熱關系的影響，根據超臨界流體的物性狀態把超臨界流動工況分為三個不同溫區，分別是擬臨界溫度附近、物性變化劇烈的擬臨界區，溫度遠高于擬臨界溫度的擬氣體區，以及溫度遠低于擬臨界溫度的擬液體區。Zahlan[25]用以下準則劃分這三個區域：

其中臨界壓力c=22.064 MPa，擬臨界溫度pc單位為。

標準回歸系數SRC（Standard Regression Coefficient）是標準化后的自變量與目標函數的線性回歸系數，其相對大小反映了自變量與因變量之間關聯關系的強弱。不同物性狀態分區中自變量與的SRC如圖2所示。可以看到，不同分區的SRC差異較大，尤其是r、B在不同區域有數倍的差異。由于線性回歸系數可以看做是一個復雜關系在一定范圍內一階偏導數的期望值，因此，本文認為無量綱數與換熱強度的關系可能由某個復雜的非線性關系所表達，而這一非線性關系的一階偏導數平均值在各物性狀態分區內并不相同，這就形成圖2中的分區表現。

圖2　不同物性狀態分區各變量SRC

為驗證換熱系數與自變量組的非線性關系，引入核嶺回歸法。嶺回歸法相對Lasso回歸改用用了模型系數的2-范數作懲罰，約束了變量間的共線性對模型系數的影響：

表4　本文選取的常用核函數

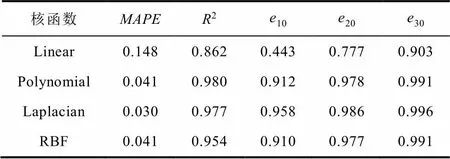
表5　各核函數所建立模型的評價

3.3　非線性關系的變量間比較分析

定義Lasso模型的殘差為：

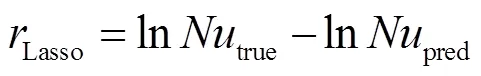
決策樹逐級生成判斷條件，以條件的“是”和“否”將變量空間不斷二分，最終把變量空間劃分為若干個對應著不同輸出結果的子空間，每個判斷條件應使得當前層級上“是”空間和“否”空間的信息增益（即信息熵在空間二分后的熵減，本問題中使用絕對誤差衡量信息熵）最大化：

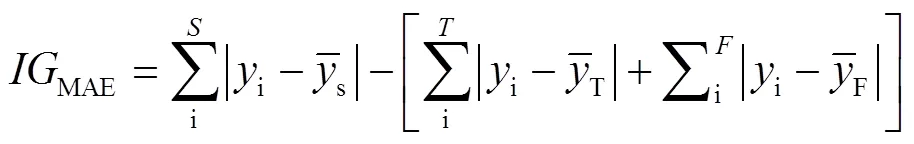
決策樹較易陷入過擬合，隨機森林通過引入隨機性構造多顆不同的決策樹并輸出各決策樹平均結果改進了模型的泛化性能，更適合于實際工程應用。隨機森林模型中，可以根據變量帶來的信息增益之和來衡量變量對于目標問題的重要度：

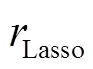
表6　不同樹深度下的變量重要度

4　換熱關聯式的建立

4.1　非線性關聯形式探究

在引入后計算公式（12），可以把非線性關系更“集中”到密度比這一變量上。畫出各數據樣本上與之間的趨勢如圖3所示。

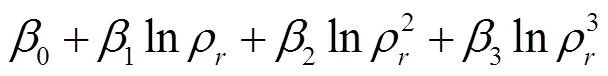
表7　猜想非線性形式的評價

顯然對數型的非線性模型效果最優，于是把對數型的非線性模型寫成公式（16）。值得一提的是，此時給出的最終公式（16）是對數型非線性模型在整個均衡化數據集上優化的結果，而非訓練集。

根據本文數據庫的覆蓋范圍，公式（16）的推薦使用范圍為：=0.006～0.038 m，=22.4～31.03 MPa，=200～3 500 kg/m2·s，=37～2 000 kW/m2，b=256～2 968 kJ/kg。

4.2　關聯式評價

用得出的關聯式對本文數據庫中的樣本進行預測，效果如圖4所示。

圖4　新關聯式的預測效果

本文挑選了9個現有關聯式與本文關聯式進行對比，包括早期研究中評價較好的Yamagata、Watts的關聯式，以及7個在大規模數據集上得到的寬范圍關聯式，計算這些關聯式的5項評價指標、2、10、20、30，見表8。前文關聯式中Jackson，Mokry，劉鑫，Yu的關聯式效果相對較好；而本文關聯式的相比其余中最好的Mokry關聯式還下降了近一半，2達到0.9以上，并且在各個誤差帶內都顯示出了明顯的優勢。

表8　本文關聯式和其他關聯式的評價對比

進一步地，針對超臨界流動傳熱較難預測的擬臨界區傳熱強化和傳熱惡化兩類典型特征，本文挑選了Lei[11]的傳熱強化和傳熱惡化實驗數據各一組，展示現有關聯式和本文關聯式在該區域內對的預測能力，如圖5和圖6所示。樣例實驗的不確定度如表9所示。可以看出本文提出的關聯式在全范圍內能夠較為緊密地跟隨傳熱強度的突升和突降趨勢。

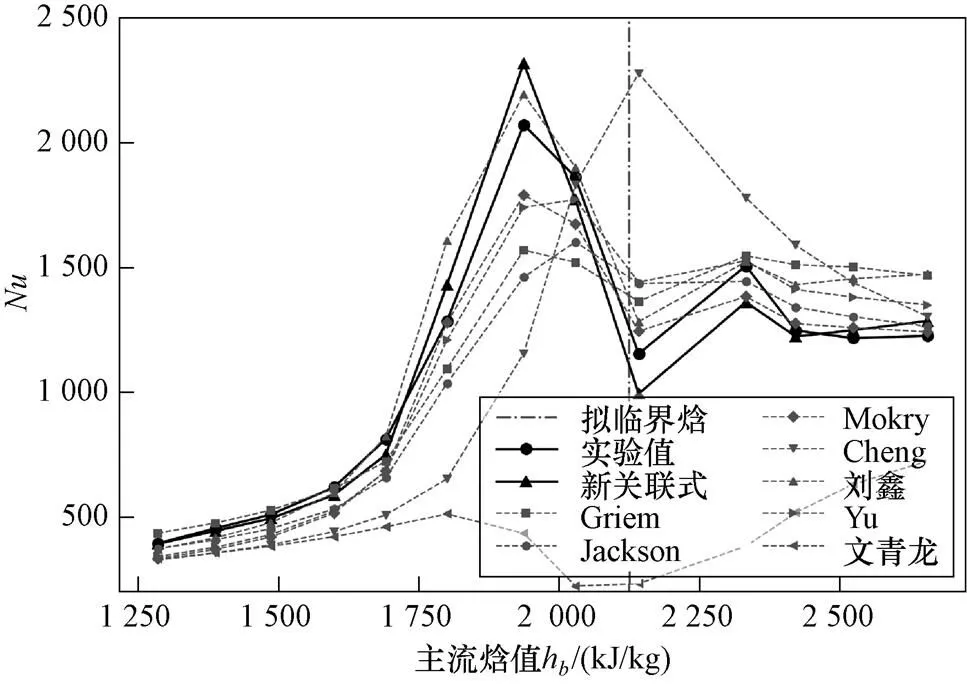
圖5　不同關聯式對傳熱強化數據預測能力的比較

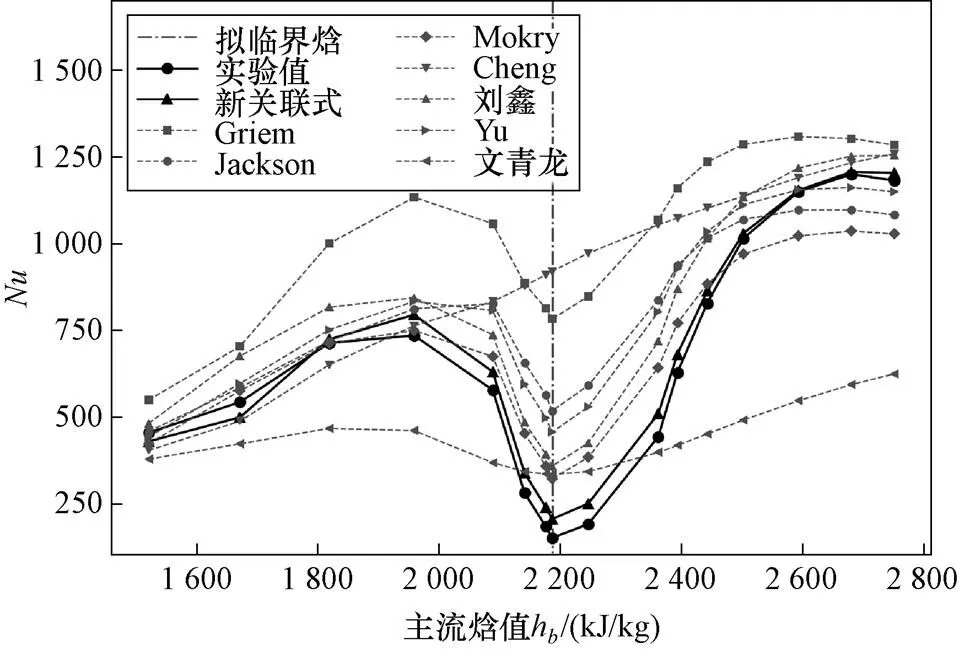
圖6　不同關聯式對傳熱惡化數據預測能力的比較

表9　樣例實驗的不確定度

5　結論

本文在搜集、整理并建立超臨界水豎直管內上升流換熱實驗數據庫的基礎上，運用機器學習方法進行數據分析，并得到以下結論：

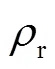
（2）通過密度比非線性成分的趨勢分析和客觀評價指標的比較，建立了基于對數型密度比項的超臨界水換熱關聯式，新關聯式的預測結果與數據庫的實驗數據符合較好；較以往此類關聯式，新關聯式預測能力有較大提升，尤其在以往預測效果不佳的擬臨界區。

［1］ Jackson J D．Models of heat transfer to fluids at supercritical pressure with influences of buoyancy and acceleration［J］．Applied Thermal Engineering，2017，124：1481-1491．

［2］ Swenson H S，Carver J R，Kakarala C R．Heat Transfer to Supercritical Water in Smooth-Bore Tubes［J］．Journal of Heat Transfer，1965，87（4）：477-483．

［3］ Vikhrev Y V，Barulin Y D，Kon’Kov A S．A study of heat transfer in vertical tubes at supercritical pressures［J］．Thermal Engineering，1967，14（9）：116-119．

［4］ Ackerman，J．W．Pseudoboiling Heat Transfer to Supercritical Pressure Water in Smooth and Ribbed Tubes［J］．Journal of Heat Transfer，1970，92（3）：490．

［5］ Yamagata K，Nishikawa K，Hasegawa S，et al．Forced convective heat transfer to supercritical water flowing in tubes［J］．International journal of heat and mass transfer，1972，15（12）：2575-2593．

［6］ Griem H．A new procedure for the prediction of forced convection heat transfer at near-and supercritical pressure［J］．Heat and Mass Transfer，1996，31（5）：301-305．

［7］ Mokry S，Pioro I，Kirillov P，et al．Supercritical-water heat transfer in a vertical bare tube［J］．Nuclear Engineering & Design，2010，240（3）：568-576．

［8］ 胡志宏．超臨界和近臨界壓力區垂直上升及傾斜管傳熱特性研究［D］．西安：西安交通大學，2001．

［9］ 徐峰，郭烈錦，毛宇飛，等．超臨界壓力下水在垂直加熱管內傳熱特性的實驗研究［J］．西安交通大學學報，2005，39（5）：468-471．

［10］黃志剛，李永亮，曾小康，等．豎直圓管通道內超臨界水傳熱實驗及數值模擬研究［J］．原子能科學技術，2012（07）：35-39．

［11］ Lei X，Li H，Zhang W，et al．Experimental study on the difference of heat transfer characteristics between vertical and horizontal flows of supercritical pressure water［J］．Applied Thermal Engineering，2017，113：609-620．

［12］ Zhang G，Zhang H，Gu H，et al．Experimental and numerical investigation of turbulent convective heat transfer deterioration of supercritical water in vertical tube［J］．Nuclear engineering and design，2012，248：226-237．

［13］王飛，楊玨，顧漢洋，等．垂直管內超臨界水傳熱實驗研究［J］．原子能科學技術，2013，47（6）：933-939．

［14］潘杰，楊冬，董自春，等．垂直上升光管內超臨界水的傳熱特性試驗研究［J］．核動力工程，2011，32（1）：75-80．

［15］趙萌．典型流道內超臨界水流動傳熱實驗和數值模擬研究［D］．上海交通大學，2017．

［16］王磊．垂直圓管內超臨界水的傳熱特性研究［D］．上海：上海交通大學，2012．

［17］張思宇，陳佳躍，趙萌，等．超臨界壓力下豎直圓管內不同流體的傳熱特性［J］．原子能科學技術，2016，50（8）：1395-1401．

［18］ Jackson J D，Cotton M A，Axcell B P．Studies of mixed convection in vertical tubes［J］．International Journal of Heat & Fluid Flow，1989，10（1）：2-15．

［19］ Shitsman M E．Temperature conditions in tubes at supercritical pressures［J］．Teploenergetika，1968，15（5）：72-77．

［20］ Herkenrath H，M?rk-M?rkenstein P，Jung U，et al. W?rmeübergang an Wasserbei Erzwungener Str?mungim Druckbereichvon 140 bis 250 bar［J］．EURATOM，EUR，3658．

［21］ Alferov N S，Rybin R A，Balunov B F．Heat transfer with turbulent water flow in a vertical tube under conditions of appreciable influence of free convection［J］．Thermal Engineering，1969，16（12）：90-&．

［22］ Lee R A，Haller K H．Supercritical water heat transfer developments and applications［C］//International Heat Transfer Conference Digital Library．Begel House Inc.，1974．

［23］王大榮，張忠占．線性回歸模型中變量選擇方法綜述［J］．數理統計與管理，2010（04）：615-627．

［24］ Zahlan H，Tavoularis S，Groeneveld D C．A look-up table for trans-critical heat transfer in water-cooled tubes［J］. Nuclear Engineering and Design，2015，285：109-125．

［25］唐亙．精通數據科學：從線性回歸到深度學習［M］．北京：人民郵電出版社，2018：227-241．

［26］ Watts M J，Chou C T．Mixed convection heat transfer to supercritical pressure water［C］//International Heat Transfer Conference Digital Library．Begel House Inc.，1982．

［27］ Cheng X，Yang Y H，Huang S F．A simplified method for heat transfer prediction of supercritical fluids in circular tubes［J］．Annals of Nuclear Energy，2009，36（8）：1120-1128．

［28］劉鑫，匡波．豎直上升管中超臨界水的寬范圍換熱關聯式［J］．核科學與工程，2012，32（4）：344-353．

［29］ Yu J，Jia B，Wu D，et al．Optimization of heat transfer coefficient correlation at supercritical pressure using genetic algorithms［J］．Heat and Mass Transfer，2009，45（6）：757-766．

［30］文青龍，王弘揚，趙萌，等．垂直圓管內超臨界水傳熱關聯式研究［J］．核動力工程，2017，38（2）：15-18．

Wide-range Data Analysis of Supercritical Water Convection Heat Transfer and Establishment of Heat Transfer Correlation

CAI Wenyi，KUANG Bo

（Shanghai Jiao Tong University，Shanghai 200240，China）

Due to the complex physical property changes of supercritical fluid in the pseudo-critical region，the convective heat transfer mode of the tube flow is very different from that of subcritical fluid．In addition to experimental research and theoretical analysis，many scholars have established supercritical fluid heat transfer correlation for the prediction of heat transfer coefficient，but none of the existing correlation can achieve satisfactory prediction results over a wide range of parameters．Therefore，based on the established heat transfer experiment database of the vertical upflow of supercritical water，the machine learning methods are used to analyze the relationship between the typical dimensionless numbers that have impact on heat transfer and the Nusselt number．According to objective evaluation indicators，appropriate correlated form is selected and a new heat transfer correlation is established．The results of non-linear analysis of heat transfer relationship show that this nonlinearity is most pronounced in the density ratio．Combining the trend of the non-linear characteristics and the evaluation results of objective indicators，the logarithmic density ratio term is introduced into the heat transfer correlation，thereby a wide-range heat transfer correlation of the vertical upflow of supercritical water is established and its prediction performance on the database is much better than existing correlations．

Supercritical water；Heat transfer correlation；Wide-range heat transfer experiment database；Machine learning

TK124

A

0258-0918（2021）03-0471-08

2020-07-21

蔡文熠（1995—），男，福建三明人，碩士研究生，現主要從事反應堆熱工方面研究