基于非下采樣輪廓波變換的中子/X射線圖像融合算法研究

賀林峰，張曉敏，武梅梅，林　強，袁石磊，劉曉光，楊　民,*

基于非下采樣輪廓波變換的中子/X射線圖像融合算法研究

賀林峰1，張曉敏2，武梅梅1，林強2，袁石磊3，劉曉光1，楊民2,*

（1. 中國原子能科學研究院，北京102413；2. 北京航空航天大學，北京 100191；3. 河南華探檢測技術有限公司，河南鄭州 450000）

由于中子與X射線的成像特性存在很好的互補性，將這兩種成像模式下的DR（Digital Radiography）圖像進行融合，可以豐富圖像細節的信息量。本研究提出了基于簡化脈沖耦合神經網絡（PCNN）的非下采樣輪廓波變換（NSCT）域中子/X射線圖像融合算法，所提出的方法通過NSCT算法對源圖像進行多尺度、多方向分解，有效地保留了各層信息，使得融合圖像展現出良好的清晰度和對比度。同時，為了更好地保留源圖像的信息，本研究對圖像的不同頻帶分別采用取平均、絕對值取大和結合PCNN系數的融合規則進行融合。通過選取結構較為復雜的石英表、機械表以及結構相對較為簡單的U盤進行中子與X射線圖像采集，并利用多種客觀評價指標定量評價基于小波變換融合、拉普拉斯變換融合、NSCT融合、NSCT-PCNN融合、Zhu的方法以及本文提出的方法生成中子與X射線融合圖像的質量。實驗結果證明，本文所提出的融合算法能夠顯著提高圖像融合效果，獲得清晰的目標信息，提高了圖像對比度，同時保留豐富的細節信息，在客觀評價標準和視覺效果上均優于其他典型方法。

圖像融合；非下采樣輪廓波變換；脈沖耦合神經網絡；中子圖像；X射線圖像

X射線成像與中子成像作為兩種重要的輻射成像方式，近些年來在材料學、生物醫學、航空航天、汽車工業、電子、考古、安檢等領域的無損檢測中發揮著越來越重要的作用[1,2]。眾所周知，X射線和中子與物質的作用機理不同，X射線作用于物質原子核外電子，其作用截面與核素的原子序數有確定的函數關系，而中子則是直接與原子核相互作用，散射截面大小與原子序數沒有直接關系。由此可見，中子成像與X射線成像特性存在著很好的互補性，中子成像在檢測含較輕元素的材料、原子序數相近元素等方面有著X射線無法具備的優勢，而X射線在檢測金屬材料、高密度物質時具有更高的靈敏度。因此，對于檢測含有金屬和非金屬材質的復雜結構樣品，利用中子成像和X射線成像兩種成像手段，可以獲得樣品更為全面的成分及結構信息。

圖像融合是將不同場景的圖像傳感器獲得的多源圖像或同一場景中不同模式的圖像進行信息合成，以獲得具有多元信息的融合圖像。與源圖像相比，融合圖像提取了來自多個圖像的互補和冗余信息，因此，更加詳盡地描述了場景信息[3]。所以，利用圖像融合技術將中子成像與X射線成像得到的圖像進行綜合處理，可以豐富圖像的邊緣、紋理等細節信息，生成質量更高的圖像。

本研究中，針對中子成像與X射線成像兩種模式下的圖像融合，提出了一種基于非下采樣輪廓波變換（NSCT）分解的圖像融合方法。通過NSCT對兩種模式的圖像進行多尺度、多方向分解后，我們對中子圖像與X射線圖像中低頻子帶、低層高頻子帶和頂層高頻子帶分別采用了不同的融合規則以保留圖像更多的細節信息。在低頻子帶融合時，考慮到直接取平均會導致邊緣信息不夠精細，本文將Sobel邊緣檢測算法引入到低頻子帶融合系數的選取規則中。高頻子帶蘊含了輸入圖像中的細節信息和特征，采用絕對值取大規則可以保留豐富的細節信息，但是由于中子與X射線圖像信噪比較差，噪聲信息分解后高頻系數較大，導致融合后圖像噪聲問題仍然明顯。因此，在對高頻子帶系數進行選取時，在相對低層的高頻子帶中使用取大融合規則，保證待融合圖像中原有的細節信息不丟失，而在頂層高頻子帶中使用簡化的PCNN模型來選取融合系數，在該模型中，采用拉普拉斯能量和矩陣與能見度矩陣作為其鏈接強度，進而實現了對噪聲的抑制。實驗結果表明，所提出的方法在中子成像與X射線成像的圖像融合中達到了較好的融合效果，不僅能夠保留X射線圖像的金屬材料信息，而且可以展現中子圖像的非金屬材料信息，融合圖像具有較高的對比度，目標信息顯著，細節信息豐富。

1　基于非下采樣輪廓波變換的中子/X射線圖像融合算法

1.1　非下采樣輪廓波變換

如圖1所示，基于非下采樣輪廓波變換（NSCT）分解過程由兩個主要的部分組成，非下采樣金字塔（Nonsubsampled Pyramid，NSP）與非下采樣方向濾波器組（Nonsubsampled Directional Filter Bank，NSDFB），NSP負責對圖像進行多分辨率分解，NSDFB則負責對圖像進行多方向分解。首先采用NSP對圖像進行多尺度分解，每經過一級NSP分解可產生一個低頻子帶和一個高頻子帶，NSP分解在低頻子帶上進行迭代以獲取圖像中的奇異點；然后對每一級的高頻子帶采用NSDFB進行多方向分解，將分布在同一方向上的奇異點合成為一個系數，從而得到不同尺度和方向的子帶圖像。

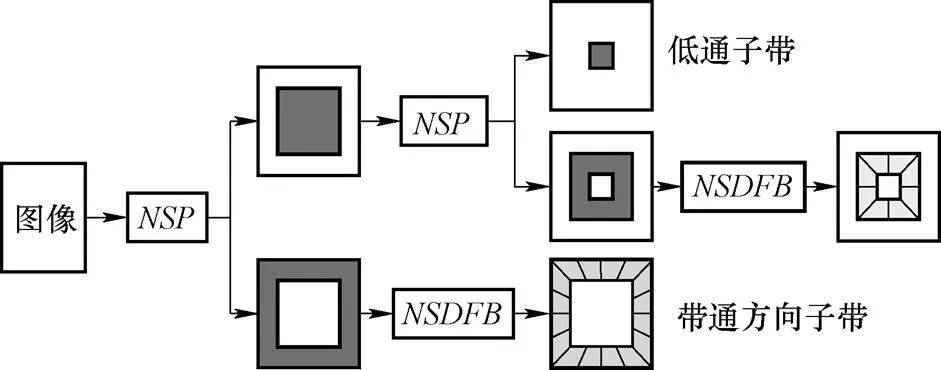
圖1　NSCT分解過程示意圖

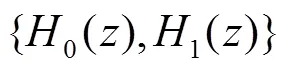
圖2　非下采樣金字塔

NSDFB分解過程中，非下采樣方向濾波器組結構如圖3（a）所示。

圖3（b）所示為非下采樣方向濾波器組的分解示意圖。第一層為扇形濾波器組，第二層為象限濾波器組，經過二層濾波可以得到圖像四個方向上的頻率子帶圖，相應頻帶劃分如圖3（c）所示。如果在此基礎之上對每一個得到的頻率子帶圖進行雙通道濾波，則可以得到八個方向上的頻率子帶圖。分解濾波器與合成濾波器同樣也需要滿足Bezout恒等式：

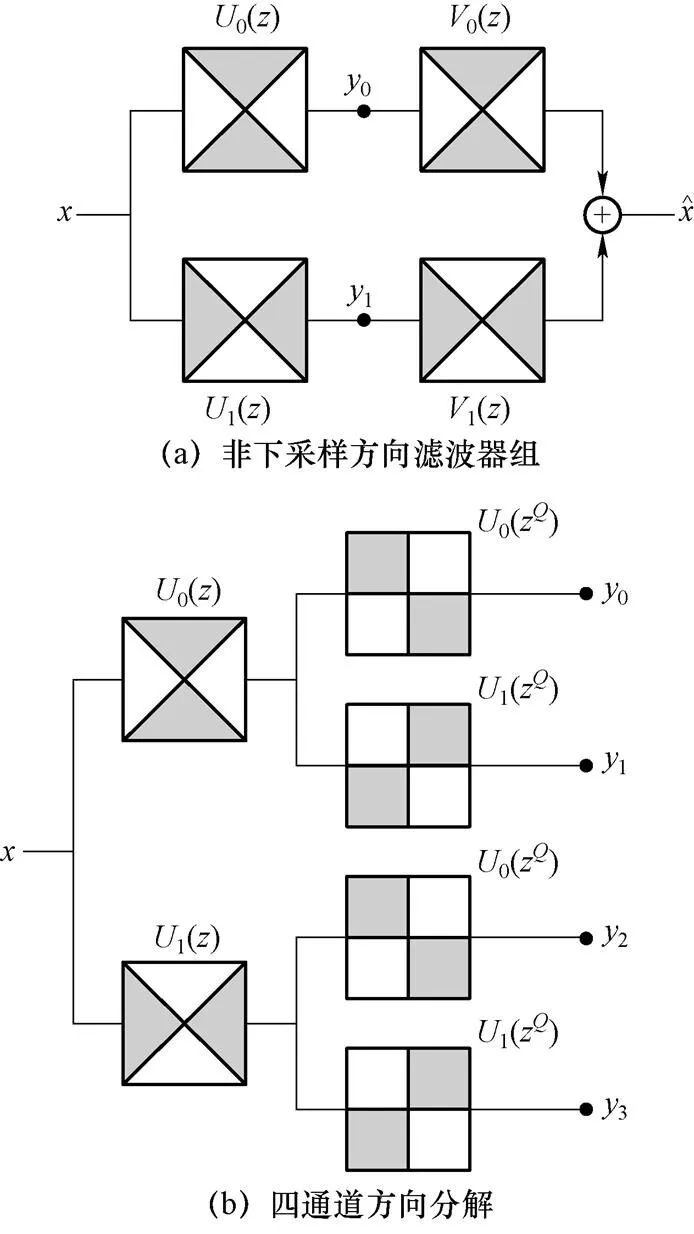
圖3　非下采樣方向濾波器組

圖3　非下采樣方向濾波器組（續）

圖4為圖像進行3級NSCT分解的示意，每個尺度下的方向分解級數為2。首先采用NSP對源圖像進行第一級分解，得到一個高頻子帶和一個低頻子帶，采用NSDFB對得到的高頻子帶進行多方向分解得到尺度一圖像；采用NSP對第一級分解得到的低頻子帶進行第二級分解，同樣可以得到一個高頻子帶和一個低頻子帶，以此類推，最終，NSCT將原圖像分解為一個低通分量和若干高通分量。可以看出，NSCT分解有效地將圖像的不同方向、不同頻帶信息進行了表示。

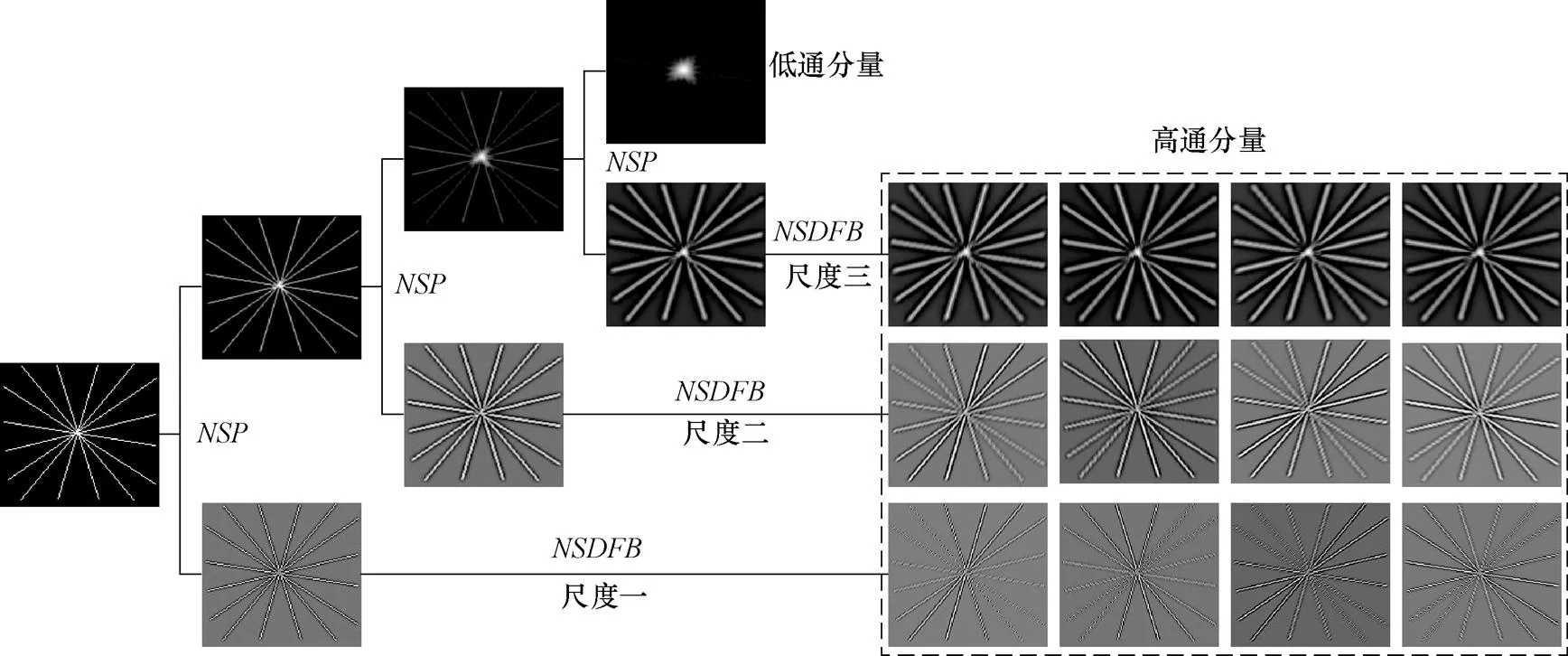
圖4　NSCT多尺度分解圖

1.2　簡化的脈沖耦合神經網絡

脈沖耦合神經網絡（Pulse Coupled Neural Network，PCNN）[4,5]具有重要的生物學背景，被稱為第三代人工神經網絡。PCNN具有神經元的全局耦合和脈沖同步特性，與真實哺乳動物視覺皮層神經元較為相近，因此更加適合于視覺系統的描述，在圖像處理領域中有著其他方法所不具備的優勢。源圖像經過NSCT多尺度、多方向分解后，各個分量的融合規則選擇會極大地影響圖像融合的質量。傳統的加權平均等方法用于高頻分量融合時會導致細節信息的丟失，不能達到很好的融合效果。PCNN具有位移、旋轉、尺度和扭曲不變的特性，能夠充分利用圖像的全局特征，將其應用到圖像融合中可以保留源圖像的更多細節信息，獲得顯著的目標信息和較高的對比度。

原始的PCNN模型非常復雜，不便于實際的應用。在盡可能減少處理性能損失的前提下，PCNN模型應盡量簡化，這樣不僅能夠提升處理效率，而且還方便實現。因此，簡化的PCNN模型不斷被提出，最常用的簡化PCNN模型[6]如圖5所示。

圖5　簡化的PCNN神經元模型[23]

式中：——當前迭代次數；

1.3　基于NSCT的圖像融合算法設計

在圖像融合的過程中，融合規則占有極其重要的地位。有效的融合規則能夠明顯提升圖像質量，豐富圖像所包含的細節信息。對于X射線與中子圖像來說，其圖像特點不同于同源圖像，且中子與X射線的成像特性差異較大，輕元素對中子衰減較大，而金屬材料對X射線衰減較大。圖像上表現為金屬材料在X射線DR圖像亮度較低，而非金屬材料在中子DR圖像上亮度較低。因此，理想的融合圖像需要將X射線圖像中金屬材料信息與中子圖像中非金屬材料信息進行融合，因此融合規則也需要進行相適應的選取。

圖像低頻子帶系數主要展現的是圖像灰度的概貌信息，常見的低頻融合方法有簡單取平均，絕對值取大以及區域能量最大化法等。X射線與中子圖像融合，屬于多源圖像融合，在融合時直接取平均可以保留兩幅圖像低頻基本的灰度信息，能夠有效地將二者的金屬材料及非金屬材料的基本信息進行整合并體現在融合圖像上，但是對于邊緣處理不夠精細，因此本文中，首先對輸入的低頻圖像利用Sobel邊緣檢測算法進行邊緣檢測[7]。對于檢測得到的圖像1與2，其中對應邊緣處灰度值為1，非邊緣處為0，然后利用公式（4）對低頻系數進行選擇：

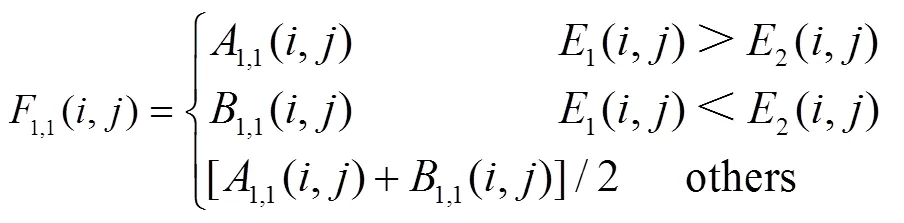
高頻子帶的系數表示了原始輸入圖像的細節信息和特征，如區域的邊緣以及輪廓邊界等，因此圖像細節信息的豐富程度與高頻子帶系數直接相關。高頻子帶系數較大的，表示區域的對比度較大，圖像更加清晰，所以在高頻子帶的融合規則中需要選取系數絕對值大者，可以將X射線圖像中金屬材料與中子圖像中非金屬材料的邊緣、紋理等細節信息提取出來并融合。但是這樣引入的問題就是當原始輸入圖像存在噪聲時，由于噪聲經過分解后的高頻系數較大，導致融合后圖像噪聲問題仍然明顯。尤其對于本文中的中子圖像，受低中子產額以及成像過程中的γ射線的影響，往往信噪比較低，圖像噪聲水平相對X射線明顯更高。因此，在高頻子帶的系數選擇中，在相對低層的高頻子帶中使用絕對值取大融合規則，保證待融合圖像中原有的細節信息不丟失，而在頂層高頻子帶中使用結合PCNN的融合規則，在選取系數時考慮周圍像素點的影響，進而對中子圖像噪聲進行抑制。

（1）取大融合規則

取大融合規則本質上是選取兩幅圖像中系數相對較大、能量較高的系數作為最終圖像對應高頻子帶的分解表示。其計算過程可由公式（5）表示：

圖像的特征信息是由鄰域內的像素共同表示，而并非由單獨的像素點表達，所以在融合時需要考慮具有較強相關性的鄰域內像素的灰度值。拉普拉斯能量和可以很好地衡量圖像中某鄰域內圖像灰度變化的相對值以及細節信息的豐富與否。拉普拉斯能量數學表達式如公式（6）所示。

、——局部區域中心點的橫縱坐標；

圖像的能見度可以很好地衡量鄰域內某點與整個區域平均灰度的關系，并判別該點是否為鄰域內表現細節的點。圖像能見度數學表達式如公式（7）所示。

3.病理剖檢。病死雞剖析可見嗉囊充滿積液，盲腸或小腸顯著腫大，比正常腫大2～4倍，外表呈紫紅色，腸腔充滿凝固或新鮮的暗紅色血液，盲腸壁變厚，漿膜層有針尖至米粒大小的灰白色糜爛點和紫色出血點間染，腸腔內充滿許多混血內容物。

將拉普拉斯能量和與能見度作為PCNN算法的輸入激勵，在高頻子帶選取相對細節信息較為豐富的對應點的系數，其高頻子帶系數選擇流程如下：

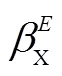
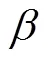
中子/X射線圖像融合算法整體流程如圖6所示。

圖6　X射線/中子圖像融合整體算法流程圖

詳細的融合過程包括以下五個步驟：

Step1. 將已配準的X射線圖像與中子圖像進行NSCT分解，得到一個低頻子帶圖像和一系列的高頻子帶圖像；

Step2. 對兩種模式下的低頻子帶圖像分別執行Sobel邊緣檢測算法，并根據公式（4）對低頻子帶圖像進行融合；

Step3. 根據公式（5）對低層高頻子帶圖像進行融合；

Step4. 將兩種模式下的頂層高頻子帶圖像進行歸一化處理并作為外部刺激輸入PCNN，計算圖像拉普拉斯能量和矩陣與能見度矩陣，然后將它們作為鏈接強度矩陣。通過簡化的PCNN為頂層高頻子帶圖像選擇融合后的NSCT系數。PCNN融合過程如下：

2）根據公式（6）至公式（7）計算兩種模式圖像的拉普拉斯能量和矩陣與能見度矩陣并作為鏈接強度；

3）以圖像歸一化灰度矩陣作為外部刺激輸入PCNN模型，根據公式（3）執行迭代步驟。

Step5. 通過NSCT逆變換重建得到融合圖像。

本文所提出的方法由于將高頻子帶分為低層高頻子帶與頂層高頻子帶兩部分，并分別采用不同的融合規則進行融合，所以在保留圖像細節信息與保持圖像對比度上有著較好的效果。同時由于頂層融合規則引入了PCNN系數，所提出的方法能夠對圖像噪聲進行一定程度地抑制。

2　實驗驗證

為了驗證本文所提出圖像融合算法的有效性，我們選取結構較為復雜的石英表、機械表以及結構相對較為簡單的U盤進行X射線與中子圖像采集。X射線圖像采集條件如表1所示。基于中國原子能科學研究院的熱中子照相裝置，我們實現了三種被檢測樣品的中子圖像采集，中子采集條件如表2所示。

表1　X射線圖像采集條件

表2　中子圖像采集條件

圖7所示為采集的中子與X射線DR圖片，針對這三種樣品的中子與X射線圖像，本研究采用小波變換融合算法、拉普拉斯變換融合算法、傳統的NSCT融合算法、NSCT-PCNN算法、Zhu等人的方法[8]以及本文所提出的算法對圖像進行融合操作，圖像融合結果如圖8所示。

圖7　中子與X射線圖像

對圖8融合結果中感興趣區域進行放大，結果如圖9所示。可以看出，Zhu等人的融合方法的凸顯了邊緣信息，但是實際樣品中的同一物質體現在圖中的灰度卻并不一致，邊緣處的梯度較大，整體主觀視覺效果較差，這會影響對樣品成分及結構信息的解讀。同時，從圖9（a）中可看出圖像融合結果的細節豐富程度以本文算法最優，NSCT-PCNN次之，拉普拉斯算法，小波融合算法和NSCT融合算法的清晰度相對較差；在圖9（b）中本文算法與NSCT-PCNN算法在保留圖像細節方面更為優秀；從圖9（c）中也可以看出本文算法融合效果明顯優于其他算法。

圖8　中子與X射線圖像融合結果

圖9　融合圖像細節放大圖

本文選取峰值信噪比、平均梯度、信息熵[9]以及空間結構相似度[10]作為評價指標對小波變換、拉普拉斯變換、NSCT、NSCT-PCNN以及本文算法的圖像融合質量進行客觀評價，其定量結果對比如圖10所示。

圖10　融合結果比較

從圖10中可以看出，本文算法除峰值信噪比相對于其他算法略低外，在平均梯度、信息熵以及空間結構相似度指標上均高于其他算法。其中，平均梯度以及空間結構相似度高于其他算法較多。

從實驗結果中可以看出，所提出的算法在圖像融合效果的主觀評價與客觀評價中均表現出優越性。相較于小波、拉普拉斯以及NSCT融合算法，本文算法與NSCT-PCNN算法的融合圖像擁有更高的清晰度；相較于NSCT-PCNN融合算法，本文算法在細節處的表現更優，其對比度以及視覺效果更好。

本文算法能夠有效地提取中子與X射線圖像的特有的特征信息，在保證源圖像細節信息不丟失的同時，可以將兩種模式下的圖像信息進行融合，并且在融合圖像中展現。如圖11所示。將配準后X射線、中子以及融合后的圖像進行對比，對其中部分細節進行放大，從整體圖與細節放大圖中可以看到，在圖11（a）中石英表的最外層邊框、表把內桿以及內部下方電池的結構由X射線圖像提供，而石英表中心結構到外殼之間的環狀區域細節以及表把外部信息在中子圖像得到展現；在圖11（b）中，機械表中心及上方的齒輪細節由X射線圖像提供，表把內部的內桿以及左側內部的細節信息由中子圖像體現；在圖11（c）中，U盤方框內的細節部分在X射線圖像得到展示，而下方細節則由中子圖像提供。

圖11　融合圖像分析

3　結論

（1）為了保留待融合圖像的整體特征，采用NSCT分解方法對中子和X射線圖像進行了多尺度、多方向的分解，得到了一幅低頻子帶圖像和一系列高頻子帶圖像。

（2）為了得到更好地融合效果，針對分解圖像的不同頻帶圖像選擇不同的融合規則。基于圖像的邊緣信息對低頻子帶圖像進行取平均融合；對底層高頻子帶圖像選取模極大值融合方法，而頂層高頻子帶則選取基于圖像拉普拉斯能量和與能見度的PCNN算法進行系數選擇。實驗結果表明，融合后圖像視覺效果更好。融合后的圖像不僅有效融合了中子與X射線圖像，而且很好地保留了二者豐富的紋理等細節信息。

（3）采用峰值信噪比、平均梯度、信息熵以及空間結構相似度作為評價指標對比了小波變換融合、拉普拉斯變換融合、NSCT融合與NSCT-PCNN融合以及本文算法的融合效果，結果表明，本文算法在圖像細節信息豐富程度、圖像對比度以及目標信息的融合方面均有著較好的表現。

本文所提出算法的主要目的是充分利用中子與X射線成像的互補特性，將這兩種成像模式下的投影數據進行融合，從而克服彼此的成像弱點，得到被檢樣品更加精準、全面和直觀的成像結果。針對不同的DR圖像以及圖像采集的條件，所提出的算法的融合參數應進行調整。同時，受采集條件所限，本文僅對DR圖像進行了融合，并沒有對中子/X射線的CT圖像進行融合。因此融合參數的自適應調整以及中子/X射線CT圖像的融合將是后續的重點研究工作。

［1］ STROBL M，MANKE I，KARDJILOV N，et al．Advances in neutron radiography and tomography［J］．Journal of Physics D：Applied Physics，2009，42（24）：243001．

［2］ YASUDA R，MATSUBAYASHI M，NAKATA M，et al．Application of neutron imaging plate and neutron CT methods on nuclear fuels and materials［J］．IEEE transactions on nuclear science，2005，52（1）：313-6．

［3］ 毛士藝，趙巍．多傳感器圖像融合技術綜述［J］．北京航空航天大學學報，2002，28（05）：512-8．

［4］ IZHIKEVICH E M．Class 1 neural excitability，conventional synapses，weakly connected networks，and mathematical foundations of pulse-coupled models［J］．IEEE Transactions on Neural Networks，1999，10（3）：499-507．

［5］ IZHIKEVICH E M．Weakly pulse-coupled oscillators，FM interactions，synchronization，and oscillatory associative memory［J］．IEEE Transactions on Neural Networks，1999，10（3）：508-26．

［6］ 苗啟廣，王寶樹．一種自適應PCNN多聚焦圖像融合新方法［J］．電子與信息學報，2006，28（3）：466-470．

［7］ JOBSON D J，RAHMAN Z，WOODELL G A．A multiscale retinex for bridging the gap between color images and the human observation of scenes［J］．IEEE Transactions on Image Processing，1997，6（7）：965-76．

［8］ ZHU Z.，ZHENG M.，QI G.，et al．A Phase Congruency and Local Laplacian Energy Based Multi-Modality Medical Image Fusion Method in NSCT Domain［J］．IEEE Access，2019，7：20811-24．

［9］ 楊艷春，李嬌，王陽萍．圖像融合質量評價方法研究綜述［J］．計算機科學與探索，2018，12（07）：1021-35．

［10］HAGHIGHAT M B A，AGHAGOLZADEH A，SEYEDARABI H．A non-reference image fusion metric based on mutual information of image features［J］．Computers & Electrical Engineering，2011，37（5）：744-56．

Neutron and X-ray Radiation Images Fusion Method Study Based on NSCT

HE Linfeng1，ZHANG Xiaomin2，WU Meimei1，LIN Qiang2，YUAN Shilei3，LIU Xiaoguang1，YANG Min2,*

（1. China Institute of Atomic Energy，Beijing 102413，China；2. Beijing University of Aeronautics and Astronautics，Beijing 100191，China；3. Henan Huatan Testing Technology Co.，Ltd，Zhengzhou of Henan Prov．450000，China）

Since thecharacteristics of neutron imaging and X-ray imaging are highly complementary，the fusion of digital radiography（DR）images of these two imaging modes can significantly enrich the information of image details．In this paper，a fusion algorithm of neutron image and X-ray image in nonsubsampled Contourlet transform（NSCT）domain based on simplified pulse coupled neural network（PCNN）is proposed．The proposed method decomposes the source image in multi-scale and multi-directional by NSCT，which effectively retains the information of each layer，so that the fusion image show good clarity and contrast．At the same time，in order to better retain the information of the source image，the different frequency bands of the image are fused by taking the average，taking the largest absolute value and the fusion rules combined with PCNN coefficients．We collect neutron and X-ray images for quartz watch and mechanical watch with complex structures and USB flash disk with simple structures．Then wavelet transform fusion，Laplace transform fusion，NSCT fusion，NSCT-PCNN fusion，Zhu’s method and the proposed method are used to fuse the neutron and X-ray images．The quality of fusion images of different methods is quantitatively evaluated by various objective evaluation indexes．The experimental results show that the fusion algorithm proposed in this paper can significantly improve the image fusion effect，obtain clear target information，improve the image contrast，while retaining rich detailed information，and is superior to other typical methods in objective evaluation criteria and visual effect．

Image fusion；Nonsubsampled Contourlet transform；Pulse coupled neural network；Neutron image；X-ray image

TL48

A

0258-0918（2021）03-0662-13

2021-03-24

國家自然科學基金項目資助（11675012）；國家重點研發計劃資助（2017YFA040370X）；國家財政部穩定支持研究經費支持，（WDJC-2019-04）

賀林峰（1981—），男，湖南人，副研究員，博士，現主要從事中子成像方面研究

楊民，E-mail：minyang.ndt@buaa.edu.cn