扭擺式MEMS電容加速度計動態性能分析

齊志華,張志勇

（中國電子科技集團公司第十三研究所，石家莊 050051)

1 引言

MEMS（Micro-Electro-Mechanical Systems）傳感器具有體積小、集成度高、成本低、性能優異、穩定性好、可靠性高等優點，被廣泛應用于航空航天、汽車導航、消費電子、工業控制等諸多領域[1]。常見的MEMS 傳感器包括加速度計、麥克風、壓力傳感器、陀螺儀、微馬達等類型，其中MEMS 加速度計是最典型和成功的應用之一。MEMS 加速度計根據不同的工作原理可以分為電容式、壓阻式、壓電式、諧振式和伺服式等類型，其中MEMS 電容式加速度計的結構原理簡單，加工工藝與IC 集成電路加工工藝兼容，集成度高，易于實現批量生產，成為應用最廣泛的加速度計傳感器之一。

系統的動態性能是衡量加速度計性能的重要指標，而系統阻尼是影響動態性能的主要參數，如何準確分析加速度計的阻尼特性和動態性能，成為加速度計設計的難點。Langlois、Bao、Pan 和Li 等[2-7]對扭擺式微平板諧振器的阻尼特性進行了分析，研究成果顯著。本研究是在已有研究的基礎上，針對扭擺式MEMS 電容加速度計，對其系統的阻尼特性和動態性能進行進一步研究和分析。

2 工作原理

扭擺式MEMS 電容加速度計主要由MEMS 敏感結構和ASIC 電路組成。當系統接收到加速度輸入時，受慣性力矩的作用，敏感結構將產生一定的轉動位移。轉動位移的變化被轉換為電容的變化量。ASIC 電路通過檢測和處理電容變化信號，最終得到能表征加速度信號大小的輸出信號，實現加速度信號的檢測。扭擺式MEMS 電容加速度計可以等效為轉動慣量-扭簧-阻尼系統，如圖1 所示。其中：J表示轉動慣量，C表示粘性阻尼系數，k表示扭轉彈簧剛度，θ表示轉角。

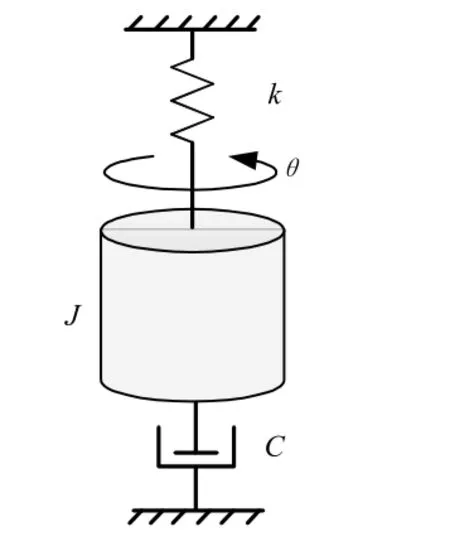
圖1 扭擺式MEMS 電容加速度計原理圖

根據牛頓第二定律可知，在加速度載荷的作用下，由于慣性力矩的作用，敏感結構將繞定軸轉動，轉角θ(t)滿足動力學方程[8]：

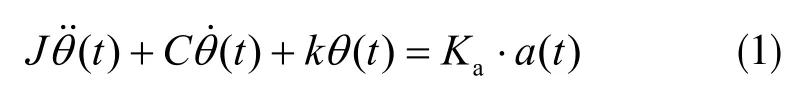
式中，Ka表示扭轉系數，a(t)表示輸入加速度，對上式進行Laplace 變化，可得到a(t)與θ(t)的傳遞函數：

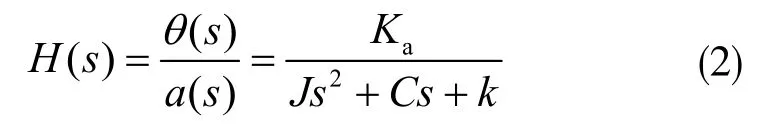
式中，s為拉氏變換的復變量，設該加速度計的無阻尼固有頻率為，阻尼比為，系統的傳遞函數可以轉化為：

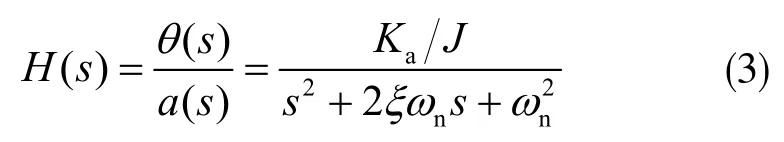
從式(3)可見，系統的動態特性與阻尼比ξ、無阻尼固有頻率ωn、轉動慣量J和扭轉系數Ka有關；而阻尼比ξ由阻尼系數C、結構剛度k和轉動慣量J決定；無阻尼固有頻率ωn由結構剛度k和轉動慣量J決定，由此可知，要分析扭擺式MEMS 電容加速度計的動態性能，需要知道C、k、J和Ka四個系統參數。

3 理論分析

扭擺式MEMS 電容加速度計的結構簡圖如圖2所示，它主要由檢測質量，彈性梁、固定端和檢測電極組成。檢測質量通過彈性梁連接到固定端，固定端固定于基板上，實現整個檢測結構的懸掛。

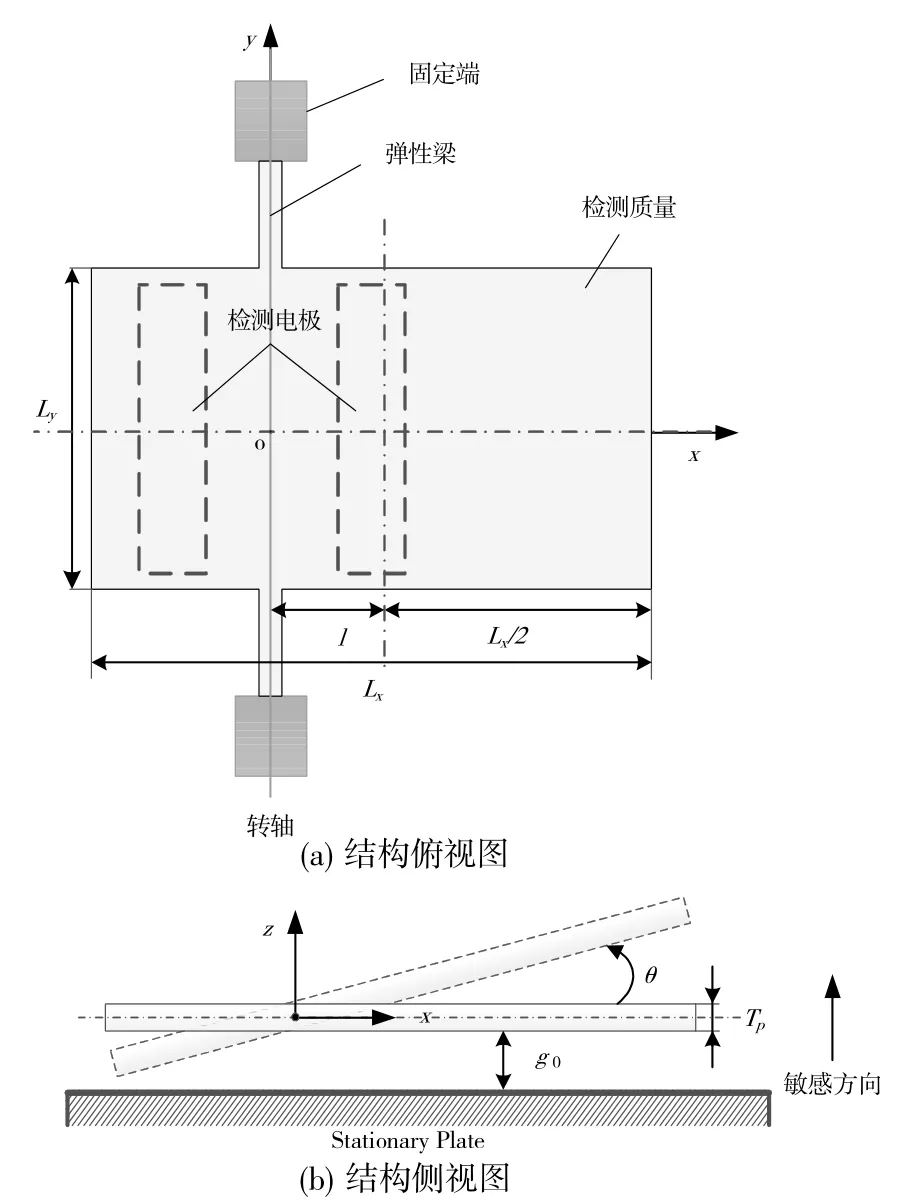
圖2 扭擺式MEMS 電容加速度計結構簡圖

圖中，Lx和Ly分別表示檢測質量的長度和寬度；l表示轉軸到檢測結構中心的距離；Tp表示結構厚度，g0表示檢測質量與基板的間隙（即薄膜氣體厚度）。當敏感方向有加速度輸入時，在慣性力矩的作用下，檢測質量會繞定軸轉動，在基板上的檢測電極與敏感質量之間形成差分電容，ASIC 電路通過檢測和處理差分電容信號最終得到輸入的加速度信號。

扭擺式MEMS 電容加速度計的彈性梁可以簡化為如圖3 所示的形式。彈性梁的一端連接到固定端，另一端連接到檢測質量。設彈性梁的長度為L，寬度為ww，高度為h，當檢測質量發生扭轉運動時，彈性梁將發生扭轉，轉角為θ。

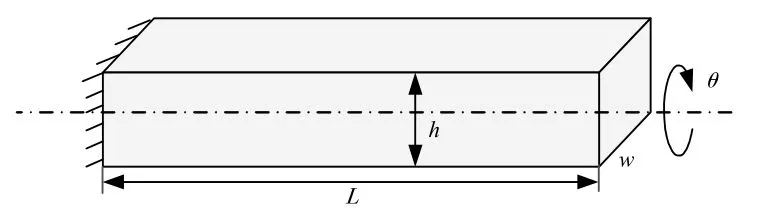
圖3 扭轉彈性梁簡化模型結構圖

根據材料力學原理，彈性梁提供的扭轉剛度為：

式中，G表示材料的剪切彈性模量。可見，扭轉剛度k與彈性梁寬度ww的三次方成正比，因此很容易通過調整彈性梁的寬度來獲得期望的扭轉剛度值。

根據動力學原理，質點的轉動慣量表示為：

式中，mo表示質點質量；r表示質點到轉軸的垂直距離。從圖2(a)可見，若將檢測質量看作是無數個質點的集合，則檢測質量的轉動慣量可以表示為：

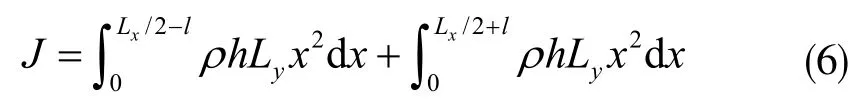
式中，ρ表示材料的密度，式(6)可以進一步簡化為：

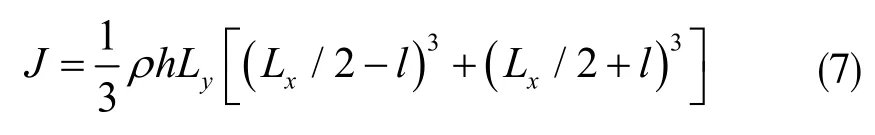
從式(7)可見，檢測質量的轉動慣量僅和其特征尺寸、材料屬性和轉軸位置有關，與結構剛度和轉動角度無關。

扭轉系數Ka表征了系統的擺動屬性，公式為：

式中，m表示結構的總質量，rc表示檢測質量的質心到轉軸的垂直距離，rc=l。

系統阻尼是決定加速度計動態性能的重要參數，阻尼效應的強弱會影響器件的工作帶寬、帶內平坦度、品質因數及機械噪聲等性能參數。扭擺式MEMS 電容加速度計的阻尼主要來源于材料內部的結構阻尼和氣體粘性阻尼。通常情況下結構阻尼比氣體粘性阻尼低幾個數量級，可忽略不計。氣體粘性阻尼分為滑膜阻尼（Side Film Damping）和壓膜阻尼（Squeeze Film Damping），各自對應的平板運動情況如圖4 所示。

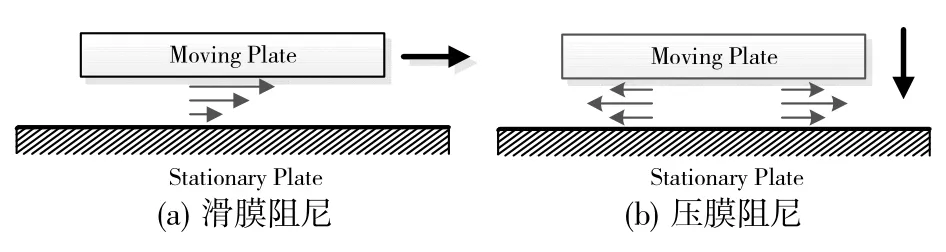
圖4 平板運動示意圖

由于敏感結構和基板間存在薄膜氣體，當敏感結構平行于基板運動時，敏感結構將帶動間隙中的氣體運動，氣體對敏感結構的反作用力即為滑膜阻尼；當敏感結構垂直于基板運動時，間隙中的氣體受到擠壓發生水平運動，氣體對擠壓產生的反作用力即為壓膜阻尼。對于扭擺式MEMS 電容加速度計，當有加速度輸入時，其工作形式為繞定軸的扭轉運動，系統的壓膜阻尼遠大于滑膜阻尼，由此，在此處僅需考慮壓膜阻尼對系統動態性能的影響。

根據Bao 等人的研究，間隙氣體的控制方程可以用Reynolds 方程表示：

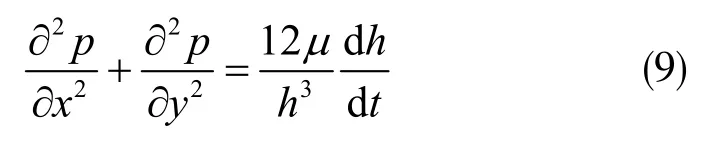
式中，p(x,y,t)=pa垣Δp，表示結構與基板間的氣體薄膜壓強，pa表示氣體壓強，Δp表示壓強的變化量；μ表示氣體的運動黏度；h(t)=g0垣xθejwt，表示間隙中氣體薄膜厚度；θ表示結構扭轉角度。對控制方程進行線性處理后，利用雙正弦三角級數近似表達氣體薄膜的壓力分布函數p(x,y,t)，可以得到擠壓模氣體對矩形板的總力矩[6]：

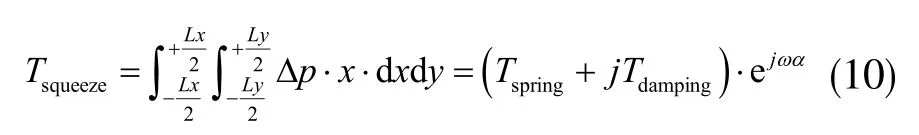
式中，α2=，μeff表示氣體的等效粘度系數。總力矩的實部Tspring=，表示氣體對結構的剛度力矩；總力矩的虛部Tdamping=，表示氣體對結構的阻尼力矩。具體表達式分別為：

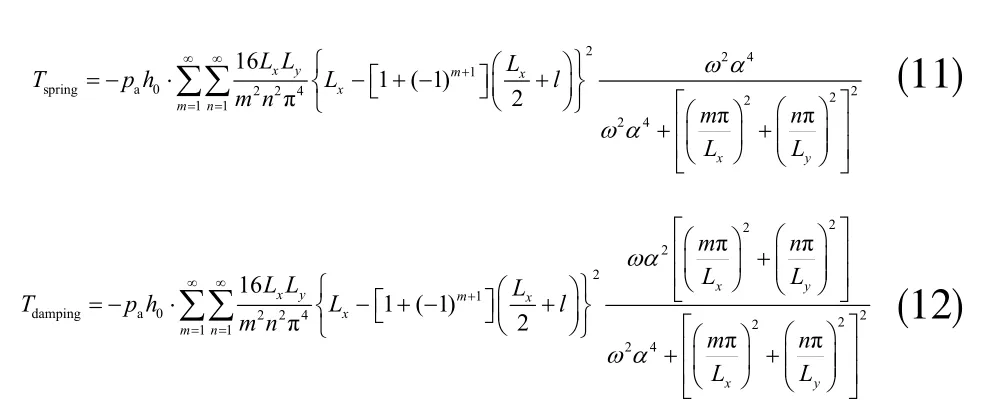
式中，m=1,2,3…；n=1,3,5…。由于剛度系數和剛度力矩，阻尼系數和阻尼力矩存在如下關系：

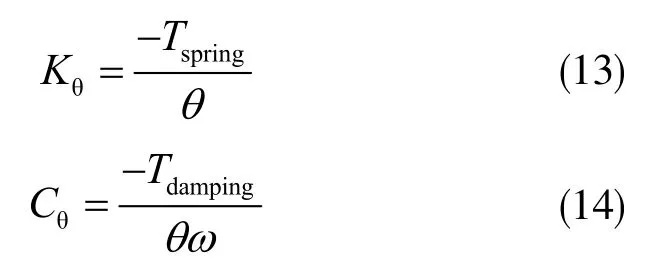
至此，即可以得到剛度系數Kθ和阻尼系數Cθ的表達式：

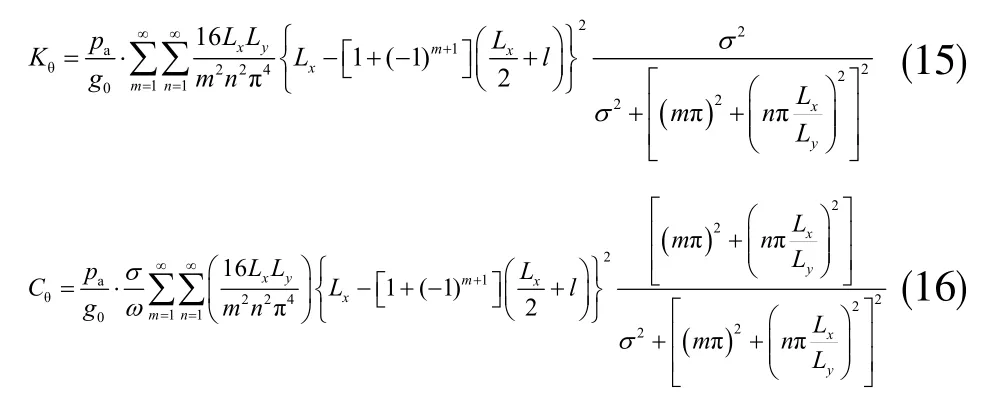
其中，σ=ωαLx2。

4 動態性能

給定一組扭擺式MEMS 電容加速度計的結構參數如表1 所示。

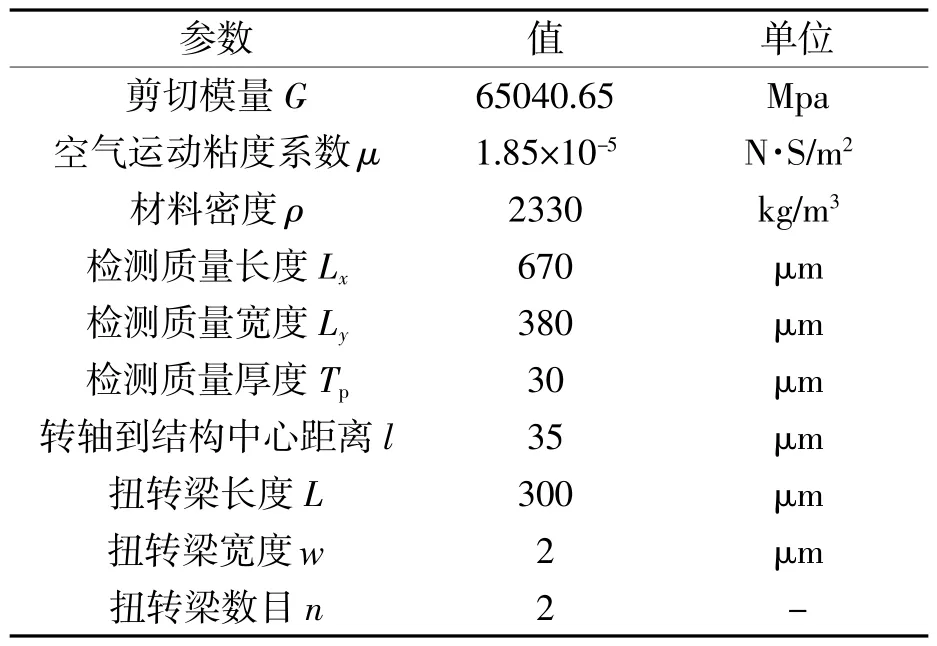
表1 扭擺式MEMS 電容加速度計結構參數

根據式(4)、(7)、(8)，可以計算得到結構剛度k=33228 μN/μm，轉動慣量J=0.00328 kg·μm2，扭轉系數Ka=6.2288×10-7kg·μm。

從式(15)、(16)可以看出，當結構的尺寸參數和材料屬性一定時，薄膜氣體的剛度系數Kθ和阻尼系數Cθ主要由氣體壓強Pa和薄膜氣體厚度g0共同決定。加速度計若采用常壓封裝，即氣體壓強為標準大氣壓（101325Pa），則剛度系數和阻尼系數隨扭轉振動頻率的變化關系如圖5 和圖6 所示。

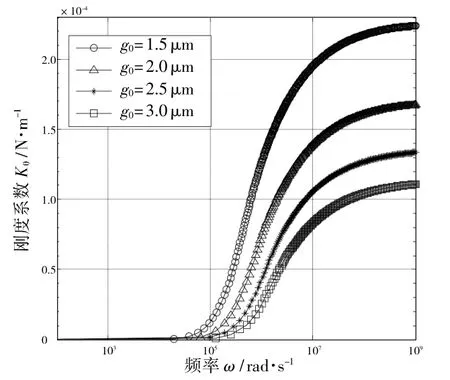
圖5 剛度系數Kθ 與振動頻率ω 關系曲線

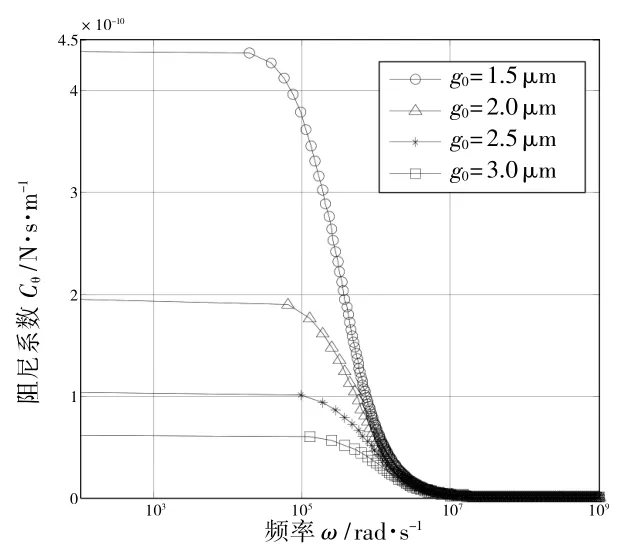
圖6 阻尼系數Cθ 與振動頻率ω 關系曲線

從圖5 和圖6 可以看出，隨著扭轉振動頻率的增大，薄膜氣體的剛度系數增大，阻尼系數減小，當振動頻率在104～106rad/s 范圍時，剛度系數急劇增大，阻尼系數急劇減小。因此，在低頻條件下氣體對結構的反作用力主要表現為阻尼效應，在高頻條件下則主要表現為剛度效應。由于開環扭擺式加速度計通常工作在低頻區，因此氣體的阻尼效應成為影響系統動態性能的主要因素。

當氣體壓強為標準大氣壓時，扭擺式加速度計的頻率響應如圖7 所示。從圖中可以看出，當氣體壓強為標準大氣壓時，扭擺式MEMS 電容加速度計由于擠壓模阻尼過大，使得傳感器的二階系統處于過阻尼狀態，系統的帶寬（-3 dB）最大約為128 Hz，很明顯這是不希望看到的。因此，在加速度計設計時常采用真空封裝或者加工阻尼孔的方式來調整系統的動態特性。

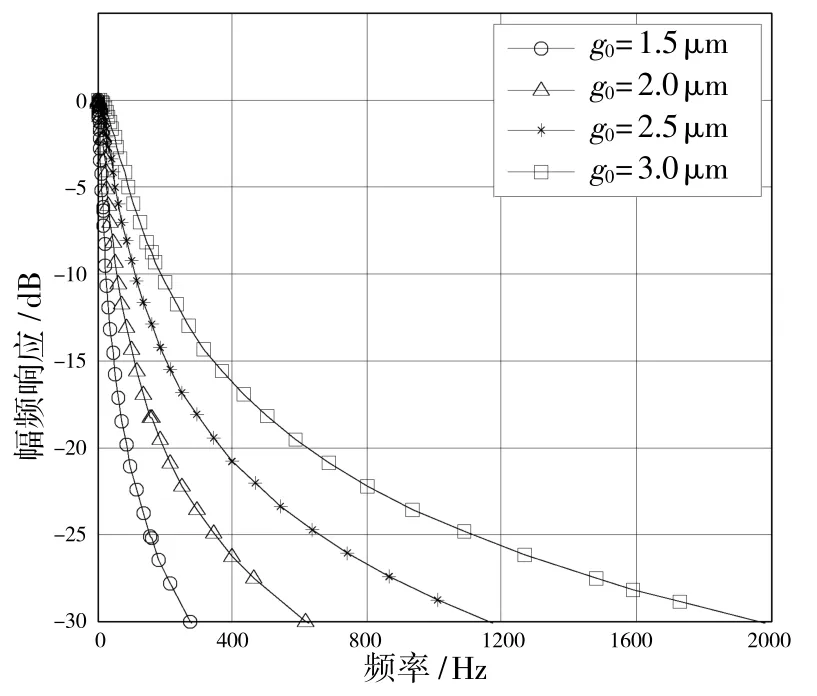
圖7 標準大氣壓下系統頻率響應曲線

若采用真空封裝或加工阻尼孔后等效氣體壓強為100Pa，則可得到傳感器的幅頻特性如圖8 所示。

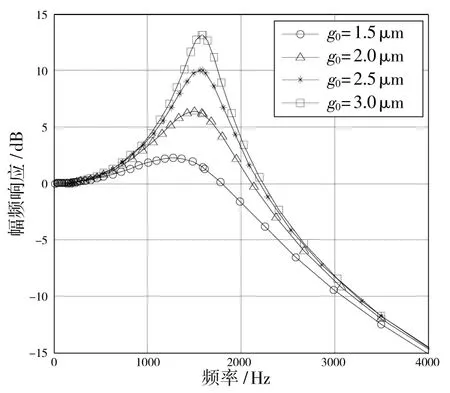
圖8 氣體壓強為100 Pa 時系統頻響曲線

可以看出，通過改變氣體壓強Pa和薄膜氣體厚度g0，容易調節系統的動態特性。根據自動控制理論可知，當系統阻尼比為ξ=時，系統有最佳的動態性能。若氣體壓強為100Pa，通過計算可以得到系統動態性能最佳時，結構與基板的間隙為1.15μm（薄膜氣體厚度），此時系統的幅頻特性曲線和單位階躍響應曲線如圖9 所示。此時系統的帶寬（-3dB）為1598Hz。

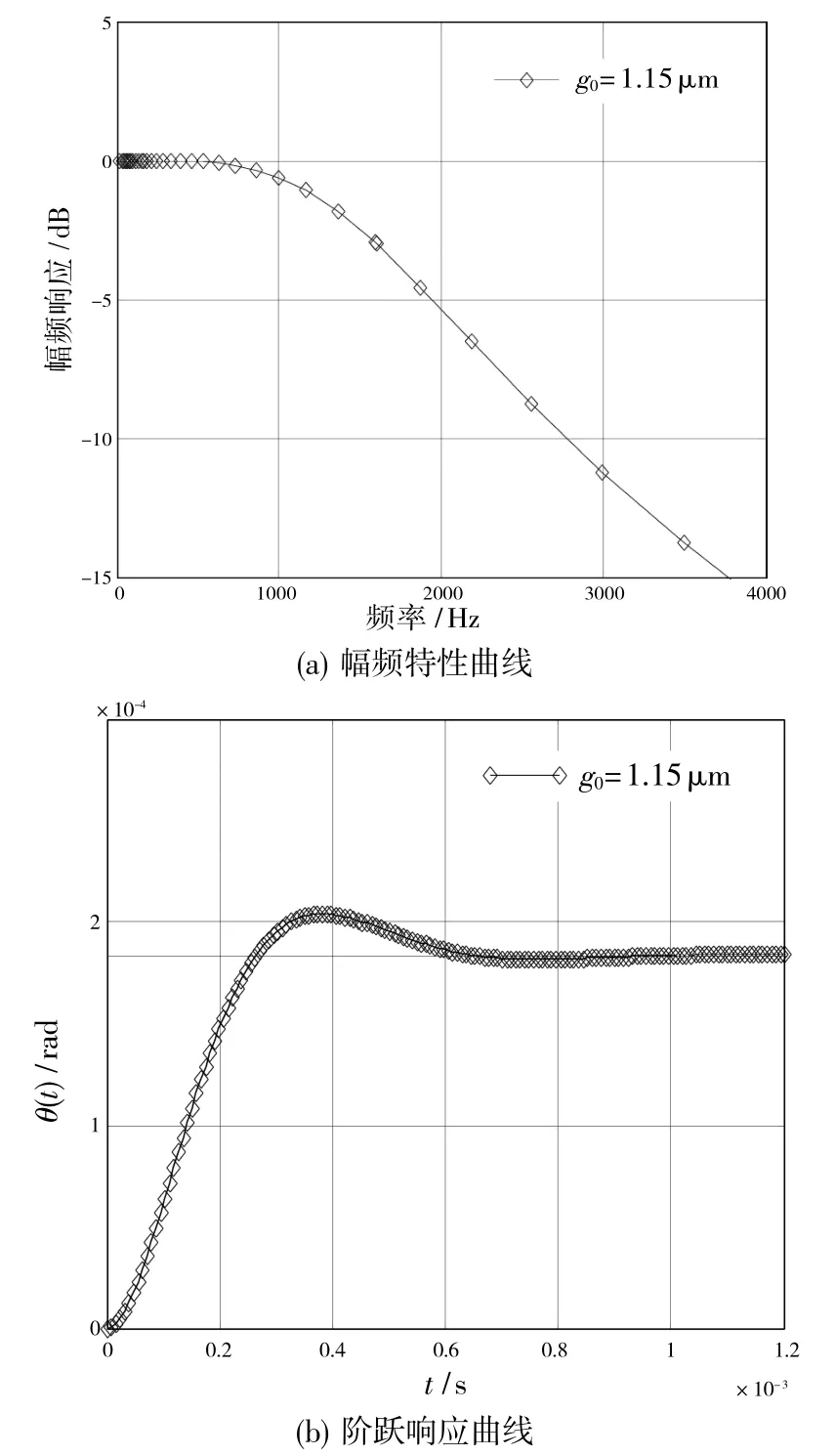
圖9 氣體壓強為100Pa 時系統幅頻特性與階躍響應

至此，基于上述分析結論，即可對扭擺式MEMS電容加速度計的動態性能進行優化設計，進而合理設計系統的結構形式和尺寸參數，最終得到綜合性能較好的加速度計。

5 結 束 語

通過對扭擺式MEMS 電容加速度計建立特征模型，對其工作原理和動態性能進行研究分析，推導出了特征模型的系統傳遞函數，給出了系統模型的結構剛度、轉動慣量、扭轉系數和阻尼系數的解析公式。在理論計算基礎上仿真了系統阻尼特性的影響因素，確定了氣體壓強和氣體薄膜厚度是最重要的影響因素。通過一組給定的結構參數，深入研究了系統阻尼特性對動態性能的影響。研究結論對于扭擺式MEMS 電容加速度計的動態性能設計具有非常重要的參考意義。