二次電子發射對系統電磁脈沖的影響*

張含天 周前紅 周海京 孫強 宋萌萌 董燁 楊薇 姚建生

(北京應用物理與計算數學研究所, 北京 100094)

系統電磁脈沖難以有效屏蔽, 會顯著影響低軌航天器等重要裝置和基礎設施的性能.為了評估二次電子對系統電磁脈沖的影響, 本文基于粒子云網格方法, 建立了三維非穩態系統電磁脈沖模型, 計算并比較了不同電流密度、金屬材料等條件下, 兩種典型結構的電磁脈沖響應.結果表明, 在計算模型中忽略二次電子發射會使部分位置的峰值電場強度被低估2-3倍, 電場響應持續的時間也會被低估10%以上.在各類二次電子中, 背散射電子對系統電磁脈沖的影響占主導, 而真二次電子的作用約為背散射電子的1/5.二次電子發射對系統電磁脈沖的影響隨著系統所用材料原子序數的增高而加大.空間電荷效應較強時, 二次電子才會對腔體外系統電磁脈沖產生影響.本研究有助于更好地通過數值模擬來獲得具體裝置在強輻射環境下的系統電磁脈沖響應.

1 引 言

系統電磁脈沖(system generated electromagnetic pulse, SGEMP)是指在γ射線和X射線(特別是由高空核爆炸釋放)的輻照下, 系統(衛星、導彈以及各種電子儀器)表面或內部產生高速運動的電子流, 進而在系統周圍激勵起的瞬態電磁脈沖[1].SGEMP不同于環境電磁脈沖, 后者是高能射線與大氣相互作用所激勵出來的大范圍惡劣電磁環境.一般情況下, 這兩類電磁脈沖不會對人員造成直接傷害, 主要毀傷作用在于干擾、損傷電子或電力系統.環境電磁脈沖對系統的影響可以通過加裝金屬屏蔽殼等常規抗電磁干擾方法屏蔽, 但是SGEMP的響應源為自身電子流, 難以有效屏蔽.SGEMP效應的毀傷效應評估以及針對性的加固設計對于保障通訊等關乎國家安全的基礎設施具有重要意義.美國于2001年成立“電磁脈沖襲擊對美威脅評估委員會”, 對十大類重要基礎設施在電磁脈沖打擊下的保護和恢復給出建議[2].

全面禁止核試驗條約的簽訂使得獲取新的SGEMP數據變得不可能, 而已公布的試驗數據也極其有限.使用較大空間范圍、高強度的射線源可以部分模擬核爆炸的輻射環境, 但此類替代實驗成本高昂、準備周期長, 出于保密等原因, 僅有一些典型簡化結構下的公開數據[3,4], 因此數值模擬成為研究SGEMP, 獲得電磁響應的重要手段.SGEMP的數值模擬研究始于20世紀70年代, 代表性成果是美國國防部原子能機構Woods等[5,6]編制的二維SGEMP數值模擬程序ABORC.該程序的準確性約在1977年美國陸軍哈瑞戴蒙德實驗室的一系列標定實驗[7]中得到了驗證.本單位相關理論計算工作與美國基本同時開展[8], 與核爆模擬裝置“閃光”-I的實驗結果總體趨勢上一致.這一階段國內外的數值模擬均以二維軸對稱腔體為研究對象, 采用粒子云網格方法(particle in cell, PIC)[9]或直接差分法求解玻爾茲曼方程[10]來描述帶電粒子的運動.

近5年來, 國內外學者在SGEMP的數值模擬方面取得了新的進展.Pointon 等[11]在報告中展示了使用二維粒子云網格-蒙特卡羅碰撞(PICMCC)方法模擬稀薄氮氣環境下內電磁脈沖結果.Angus等[12]考慮多種分子、原子亞穩態, 建立了零維反應動力學模型, 用于篩選高能電子-空氣作用中的主要反應路徑.北京應用物理與計算數學研究所孫會芳等[13]使用三維PIC方法計算真空中圓柱腔體的SGEMP.西北核技術研究院的Chen等[14]系統地研究了初級電子能譜等對空間電荷層形成特征時間的影響.中物院應用電子學研究所的Chen等[15]提出了一種描述SGEMP空間電荷層的方法, 可以有效降低PIC模擬所需計算資源.清華大學的Meng等[16,17]模擬了神光-III裝置的SGEMP響應, 并使用時偏時域有限差分法減弱電磁場中的高頻噪聲.然而, 此前的研究中大多忽略了高能電子與金屬材料作用產生的二次電子,Wenaas等[18]的二維模型中也沒有考慮彈性背散射以及真二次電子發射.為了更好地評估強輻射環境對具體裝置的影響, 本文基于PIC方法, 考慮二次電子發射過程, 建立三維非穩態SGEMP數值模擬模型, 研究各類二次電子發射機制對SGEMP數值模擬結果的影響.

2 數值模型

2.1 電磁粒子模擬方法

本文關注高能光電子、二次電子的運動以及隨之激勵出的電磁場響應, 采用PIC方法描述電子的運動[19], 該方法通常不會跟蹤所有實際粒子, 而是用“宏粒子”代表若干相鄰的電子, 粒子的位移x和速度v隨時間t的變化服從(1)式:

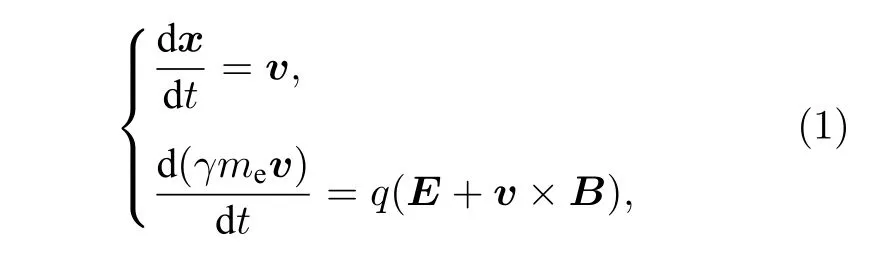
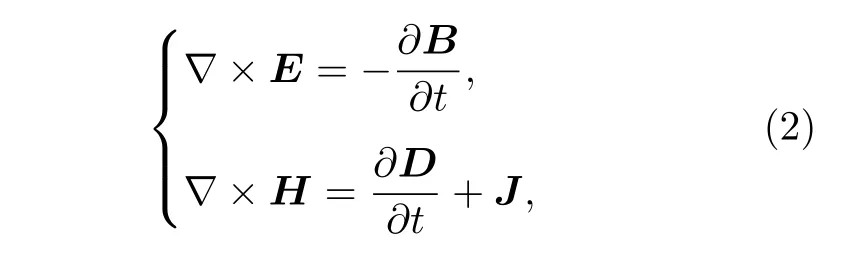
其中, H, D和J分別為磁場強度、電位移矢量和電流密度.由初始條件出發, 電磁場的更新和帶電粒子的運動交替進行.通過校正電流連續性方程來滿足空間電荷守恒[19].

2.2 二次電子發射

在具有一定能量電子的撞擊下, 固體靶表面會通過各種機制發射電子.本文主要考慮兩類二次電子, 分別是真二次電子和背散射電子.入射電子與固體靶發生非彈性碰撞, 從固體靶中激發出高于其材料功函數的電子, 稱這類電子為真二次電子[20].而部分入射電子與靶材經過一次或多次碰撞后會從固體靶表面射出, 這部分電子被稱為背散射電子, 背散射電子又可進一步細分為彈性和非彈性背散射電子.通常, 真二次電子的能量小于50 eV, 背散射電子的能量更高, 其中彈性背散射電子的能量與入射電子相當[21].背散射電子數與入射電子數之比為背散射電子發射系數(反射系數), 真二次電子數與入射電子數之比為真二次電子發射系數.除了發射系數, 在對二次電子進行建模時, 還需要明確出射二次電子的能譜與角分布.下文將分別對真二次電子和背散射電子的建模進行說明.

2.2.1 真二次電子的發射特性

真二次電子發射系數與入射電子能量Ein、角度θ以及固體靶的材料、表面光潔度相關.對于入射電子能量小于1 keV的情況, 普遍使用Vaughan模型[22]描述真二次電子發射系數.在更高的入射電子能量下, 可以利用法向入射真二次電子的發射系數δ0與入射電子能量的比例關系[23]((3)式)以及與入射電子角度的關系[21]((4)式)來近似獲得該發射系數.真二次電子的能譜和角分布設置可以基于Furman與Pivi提出的概率模型[24]:

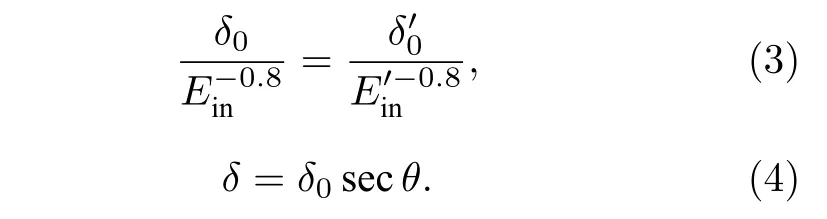
2.2.2 背散射電子的發射特性

背散射電子發射系數與入射電子能量弱相關[25],與入射電子角度、固體靶的材料強相關[18], 該發射系數可以通過實驗測量[26]或蒙特卡羅模擬[27]獲得.在數值建模中, 通常使用經驗公式來描述背散射電子發射系數, 如Hunger-Küchler公式[23], 但該公式在入射電子能量小于3.5 keV, 或固體靶材原子序數Z較大時的偏差較高[28].本文結合Staub[29]的工作, 使用如(5)式所示的法向入射電子的背散射電子發射系數?0, 該式普遍適用于0.5 keV ＜Ein＜ 100 keV, 且Z ＞ 4的情況:

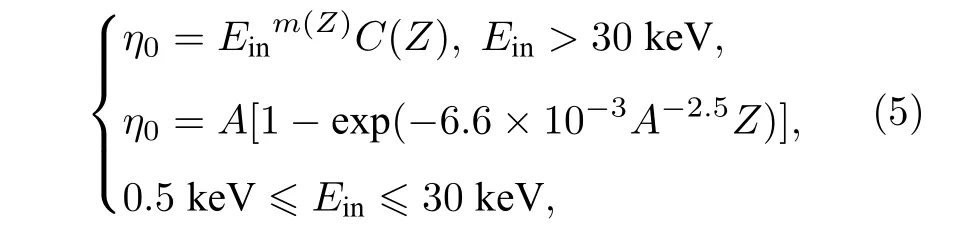
其中, 擬合參數 C(Z)=0.1904-0.2236lnZ+0.1292(lnZ)2-0.01491(lnZ)3, m(Z)=0.13182-0.9211/Z0.5, A =0.4+0.065ln(Ein) , 入射電子能量單位keV.圖1繪出了由(5)式計算出的?0以及鋁、銅、金三種材料背散射電子發射系數的實驗數據[20].除Ein= 0.5 keV的電子射入銅制靶面條件下不同實驗數據間存在較大差異外, (5)式的計算結果與實驗數據均符合得較好.

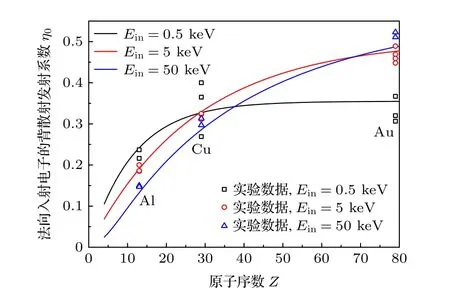
圖1 不同原子序數、入射能量條件下, 法向入射電子的背散射電子發射系數(離散點來自Joy[20]總結的實驗數據,實線由式(5)計算)Fig.1.Backscattering coefficient of normally incident electrons for different Ein and atomic numbers.Symbols, experimental data from Joy[20]; lines, calculated by Equation (5).

入射電子角度θ [0, π/2]對背散射電子發射系數?的影響可由(6)式描述[20]:

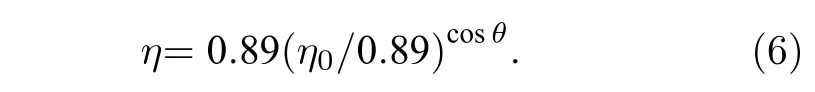
彈性、非彈性背散射電子的發射系數?els和?ine主要與固體的材料相關, Reimer[20]總結實驗數據, 給出非彈性、彈性碰撞截面之比 σine/σels≈20/Z .可得?els/? = 1-(?ine/?) = Z/(Z+20), 即金屬材料的原子序數越大, 背散射電子中彈性散射的占比越高.

彈性背散射電子的角分布可按鏡面反射處理,即散射角與入射角關于靶平面的法線對稱.非彈性背散射電子的角分布較為復雜, 是與材料、入射電子能量和入射角均相關的分布函數, 這里進行簡化處理[28], 設置非彈性散射角等于最概然散射角θinels=-27θ/40 , 式中負號表示散射電子與入射電子分別在法向量兩側.根據發生散射的類型, 分別設置背散射電子的能量.彈性背散射電子相較于入射電子基本沒有能量損失, 本模型參考劉臘群等[28]的工作, 統一設置彈性背散射電子的能量比入射電子低20 eV.而非彈性背散射電子的能量分布函數按照Matsukawa等[30]實驗測量的二次電子能譜分布來賦值, 忽略入射電子能量與入射角度對能量分布函數的影響[18,23].

2.3 計算區域和邊界條件

圖2為本文涉及的兩種典型SGEMP計算模型的示意圖.圖2(a)所述模型用于模擬X射線(沿圓柱軸向自右向左均勻射入金屬的右側端面)輻照長度為h, 半徑為R的金屬圓柱體所激發的腔體外SGEMP.X射線與固體介質相互作用并發射光電子的過程比較復雜[31].本文主要研究二次電子對SGEMP的影響, 因此對端面產生的光電子進行簡化處理, 假設其均為單能電子(能量E0), 運動方向垂直于受輻照面向外[14,17], 光電子發射面的電流密度Jemi(正比于X射線功率密度與光電產率)在時間上表現為單個脈沖且該脈沖服從正弦平方分布[13], 如(7)式所示:

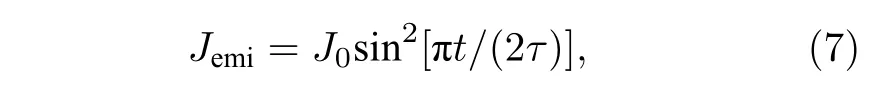
其中, 峰值電流密度為J0(A/cm2), τ為時間脈沖的半高寬, 設為1 ns.圖2(b)中的模型用于模擬封閉空心金屬腔體的內SGEMP[17], 光電子僅由左側內端面發射, 光電子的發射特性與圖2(a)所述模型一致.本文計算模型的金屬圓柱體均為正圓柱,h = 2R = 100 mm.

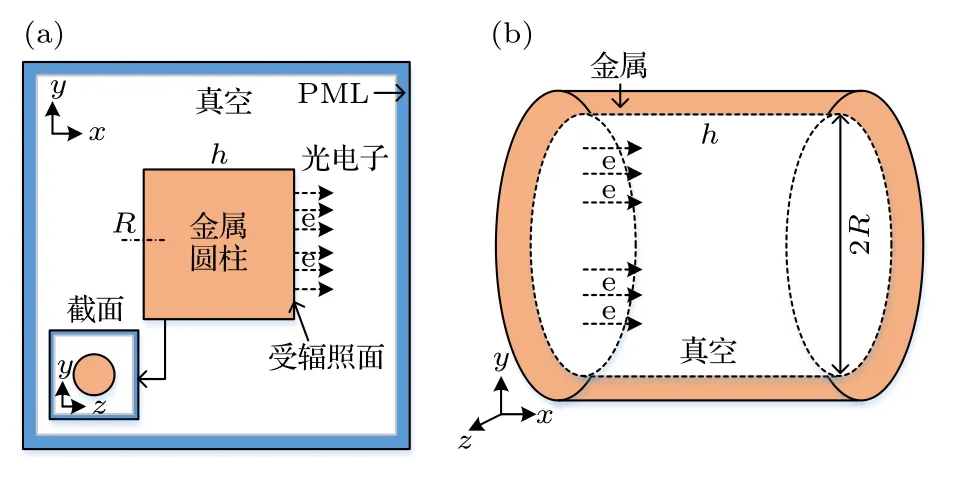
圖2 計算模型示意圖 (a)腔體外SGEMP; (b)腔體內SGEMPFig.2.Schematics of the calculation domain: (a) The external SGEMP; (b) the internal SGEMP.

在每一計算時間步中統計越過金屬邊界的宏粒子, 認為該宏粒子被金屬邊界吸收, 計算被吸收宏粒子的能量及入射角, 并按2.2節所述的發射系數釋放出若干個二次電子.電子的產生和在真空區域的運動會激發出電磁場.假設金屬為理想導體,導體內部電場、邊界上的切向電場分量和磁場強度的法向分量為零[17], 在圖2(a)中計算模型的最外側對電磁場設置理想吸收層邊界(perfectly matched layer, PML), 為減小邊緣效應, 設置PML邊界的空間尺寸為金屬圓柱尺寸的3倍[13].計算所用網格的空間尺寸為5 mm, 時間步長10-12s, 峰值宏粒子數約為106.

3 結果與討論

3.1 腔體外SGEMP

本節首先研究如圖2(a)所示腔體外SGEMP的特性, 受輻照金屬圓柱的材料為中等Z值的銅.圖3比較了是否考慮二次電子發射對電子空間分布的影響(圖3(a)-圖3(c))中包括光電子、背散射電子和真二次電子).虛線部分表示金屬圓柱, 光電子由金屬圓柱的右端面向外發射.光電子發射后會在金屬表面留下正電荷, 與光電子共同激發出電場, 當這一電場強度足夠高, 光電子會被減速, 導致大量電子聚集在金屬表面附近, 形成空間電荷層(space-charge barrier).一部分光電子無法穿出空間電荷層, 返回金屬表面.不考慮二次電子發射的情況下(如圖3(d)), 受空間電荷層作用返回金屬表面的光電子被直接吸收.對比圖3(c)與3(d),可以發現在金屬表面, 特別是右側端面, 產生了相當數量的二次電子.

圖3 不同時刻電子的空間分布(J0 = 5 A/cm2, E0 =5 keV).(a)(b)(c)考慮二次電子發射; (d)無二次電子發射的情況Fig.3.Distribution of electrons at different moments on the condition J0 = 5 A/cm2 and E0 = 5 keV: (a)(b)(c)Including secondary emission; (d)without secondary electrons.

圖4 為不同峰值電流密度條件下, 光電子發射面中心P1位置(距右端面5 mm, 如圖3(b)所示)的軸向電場強度, 根據在模型中是否考慮了二次電子發射可分別得到圖中虛線和實線所示的結果.P1處的軸向電場強度隨著時間的延長先快速上升達到峰值, 隨后趨于飽和并發生振蕩, 最后隨著發射光電子數量的降低, 電場強度快速下降至小于 5 ×105V/m.峰值電流密度升高, 初始階段軸向電場的上升速率增大, 電場強度的最大值也隨之增大.然而, 電場強度的最大值與峰值電流密度不滿足線性關系, 例如, 當峰值電流密度J0由5 A/cm2上升至100 A/cm2, 最大電場強度僅由9.6×105V/m增至 2.2×106V/m.對比是否考慮二次電子條件下的電場強度, 可發現在模型中加入二次電子過程會使飽和階段計算出來的電場增強約25%-30%, 電場在時間上的半高寬也會增寬約10%-15%.兩模型計算結果出現差異的時刻均在電場強度第一峰值后, 且該時刻隨著峰值電流密度的增大而提前, 由5 A/cm2條件下的1.81 ns提前至100 A/cm2時的0.76 ns.

如前文所述, 金屬在X射線輻照下向外發射光電子并使本身帶正電, 發射的光電子數目越多,電場強度越強, 對應著電場強度在初始階段的快速上升.然而, 該電場會阻礙光電子繼續向外運動,當受輻照面附近累計發射的光電子足夠多, 空間電荷層內的電場強度升高至使一部分光電子反向運動, 電場強度減弱, 電子返發射面降低了空間電荷層內電子數目, 進一步削弱了電場強度, 隨后更多的電子能夠進入空間電荷層, 如此反復, 導致了電場的振蕩[32].電荷累積并形成空間電荷層需要一定時間, 對于腔體外SGEMP, 在空間電荷層形成前,不會有光電子返回金屬表面, 也就不會產生二次電子, 所以圖4中最初一段時間內考慮二次電子發射不會對電場結果產生影響.定義電子首次返回發射面的時刻(也即二次電子產生的時刻)為空間電荷層產生的特征時間, 光電子能量越高、電流密度越小, 特征時間越長[14].

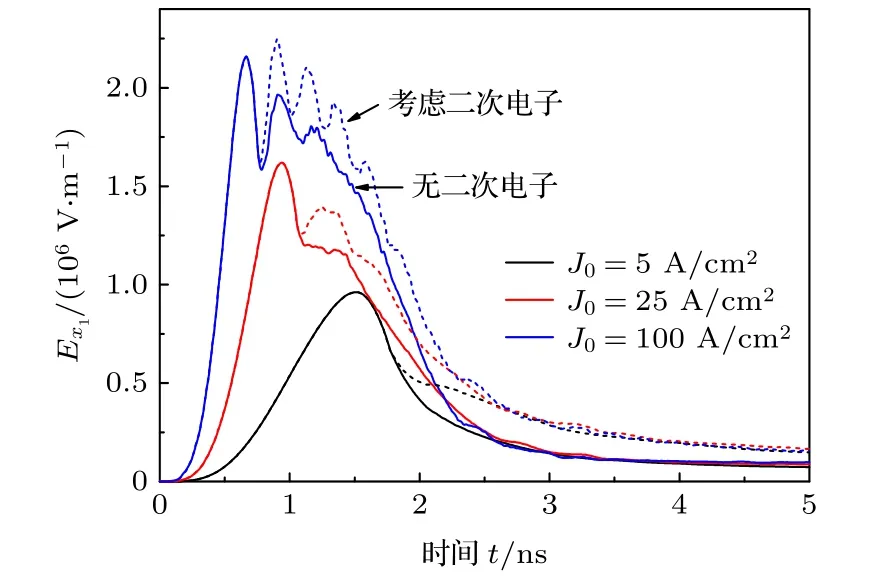
圖4 不同峰值電流密度條件下, P1位置的軸向電場強度Ex (實線: 未考慮二次電子發射, 虛線: 考慮二次電子發射, E0 = 5 keV)Fig.4.Axial electric field Ex at P1 for different peak current densities (Solid line: not including secondary electrons;dash line: including secondary electrons, E0 = 5 keV).

圖5 給出了不同峰值電流密度下, 圓柱側面中點P2處的徑向電場強度.相比于P1, P2位置電場強度受二次電子的影響更為顯著, 特別是對于峰值電流密度較強的情況.如J0= 100 A/cm2, t =3 ns, 考慮二次電子時的徑向電場強度為 1.93×105V/m, 約為不考慮二次電子條件下的1.8倍.由于P1點位于金屬受輻照面附近, 其電場強度直接受高能光電子特性以及空間電荷層的影響, 而P2位置幾乎沒有光電子, 光電子以及二次電子主要通過改變金屬的電荷分布來間接影響P2位置的電場.在持續的時間上, 考慮二次電子也會使算得的電場強度出現明顯的拖尾現象.圖中還給出了在計算模型中僅考慮二次電子里的背散射電子, 忽略真二次電子的仿真結果.對于能量5 keV的電子撞擊銅靶面的情況, 真二次電子發射系數略高于背散射電子發射系數, 但真二次電子對計算出的電場強度差異的貢獻僅為背散射電子的1/5左右.這主要是因為真二次電子的能量遠低于背散射電子, 受金屬表面電場的作用, 大部分真二次電子在產生后又迅速被金屬吸收, 所以對電場響應的貢獻有限.

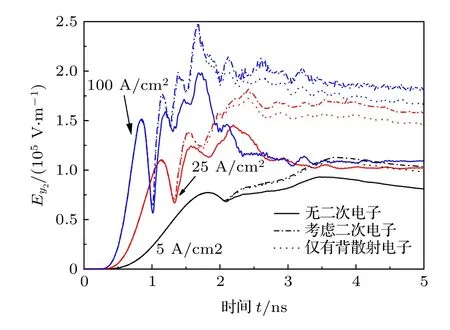
圖5 不同峰值電流密度條件下, P2位置的徑向電場強度Ey (實線: 未考慮二次電子發射, 虛線: 考慮二次電子發射, 點線: 僅考慮背散射電子, E0 = 5 keV)Fig.5.Radial electric field Ey at P2 for different peak current densities (Solid line: not including secondary electrons;dash line: including secondary electrons; dot line: only considering backscattering electrons, E0 = 5 keV).

圖6 對比了峰值電流密度5和100 A/cm2條件下, P2位置切向磁感應強度Bz.空間磁場的分布主要受金屬導體上電荷重新分布時產生的置換電流影響, 峰值電流密度越大, 磁感應強度的極值越大, 但受空間電荷層的限制, 磁感應強度的極值與峰值電流密度之間也不滿足線性關系.J0=5 A/cm2, 空間電荷效應弱, 光電子返回金屬表面所產生的二次電子較少, 對置換電流的影響也較低, 是否考慮二次電子發射對計算出的磁場基本沒有影響.提高峰值電流密度至100 A/cm2, 空間電荷效應增強, 磁感應強度會表現出明顯的振蕩, 振蕩頻率約為3.5 GHz.考慮二次電子使Bz第二負峰的幅值由 1.3×10-4T增至 2.0×10-4T, 磁場的振蕩頻率也略微升高.

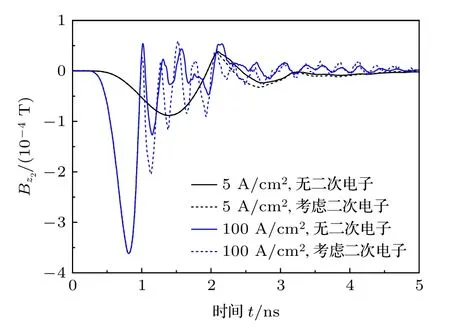
圖6 在J0 = 5, 100 A/cm2條件下, P2位置的磁感應強度BZ (實線: 未考慮二次電子發射, 虛線: 考慮二次電子發射, E0 = 5 keV)Fig.6.Magnetic field BZ at P2 for J0 = 5, 100 A/cm2 (Solid line: not including secondary electrons; dash line: including secondary electrons, E0 = 5 keV).

3.2 腔體內SGEMP

不同于3.1節的腔體外SGEMP, 本節研究的腔體內SGEMP, 其光電子的發射面在金屬腔體內部, 特別是對于封閉金屬腔體, 所有光電子都會撞擊到腔體表面, 并按一定概率產生二次電子.圖7比較了不同腔體材料對P1位置(圓柱腔體末端中心點)軸向電場強度的影響.考慮二次電子發射后, Ex1出現谷值的時刻由2.19 ns后移至約3.55 ns, 幅值由 7.56×104V/m增大至Al腔體下的 1.52×105V/m、Au腔體的 2.75×105V/m, 分別為未考慮二次電子條件下的2.01倍、3.64倍.Cu腔體條件下的電場強度變化介于Al和Au之間, 約為無二次電子條件下的2.84倍.不同材料條件下電場的脈沖寬度都發生了加寬.圖7還給出了Cu制腔體、僅考慮背散射電子條件下的計算結果, 可以發現, 真二次電子導致Ex1差異的占比隨著時間延長而逐漸增大, 5 ns時, 約為考慮二次電子導致電場總差異的24%.

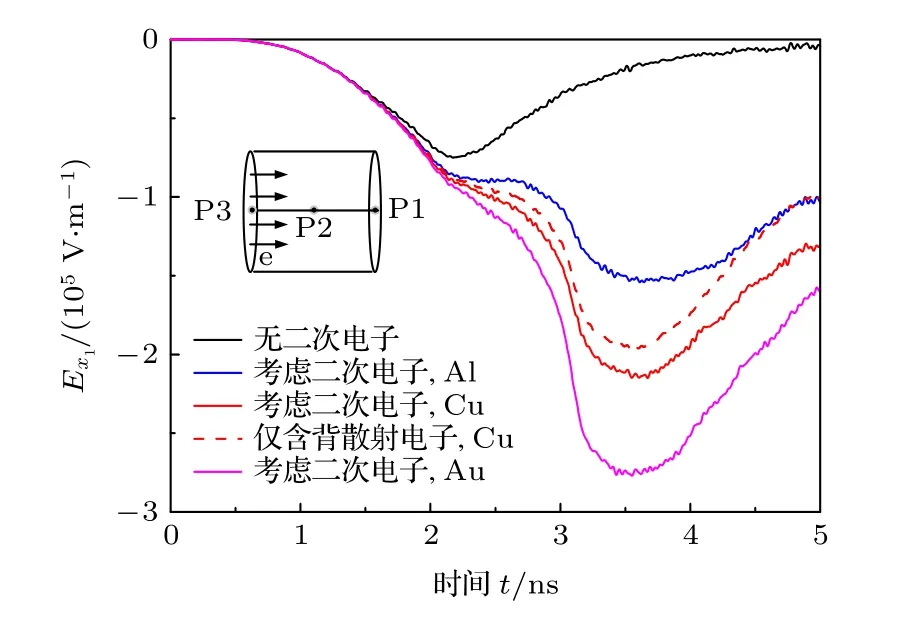
圖7 不同腔體材料, P1位置的軸向電場強度Ex(J0 =1 A/cm2, E0 = 5 keV)Fig.7.Axial electric field Ex at P1 for different materials(J0 = 1 A/cm2, E0 = 5 keV).

圖7 的結果表明, 在各類二次電子中, 背散射電子對內SGEMP的影響最為重要.在約3.5 ns后, 真二次電子導致的電場差異占比隨時間延長逐漸增大, 主要是因為金屬表面的電場幅值降低, 受該電場作用返回金屬表面的真二次電子數減小.腔體所用金屬材料的原子序數越高, 背散射電子發射系數就越大, 同時, 非彈性背散射電子能譜的峰值也向更高能量區域移動, 共同導致了高Z材料下算得電場強度差異的增大.

圖8給出了光電子發射面中心P3 (距左側端面5 mm)、軸向中點P2以及末端面中點P1 (距右側端面5 mm)三點的電場強度.可以發現, 二次電子發射對腔體內不同位置電場都有顯著影響, 如P3處電場的半高寬增加了11%(Al)-57%(Au).然而, P3處電場強度的幅值沒有發生顯著變化, 僅增大了約4%, 遠小于P1位置電場強度的變化.這主要是由于在較低的電流密度下(J0= 1 A/cm2), 光電子發射面附近累積的電子數目太少, 空間電荷限制效應較弱, 穿過空間電荷層并撞擊到腔體末端面的光電子占主導, 導致末端面二次電子發射數目大于光電子發射面附近的二次電子數, 所以P1處電場幅值的變化更大.

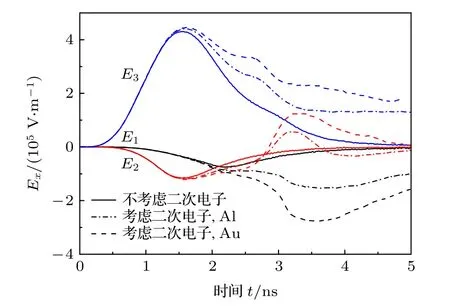
圖8 不同位置(P1, P2, P3)的軸向電場強度Ex (J0 =1 A/cm2, E0 = 5 keV)Fig.8.Axial electric field Ex at P1, P2 and P3 (J0 =1 A/cm2, E0 = 5 keV).

不同峰值電流密度下, 腔體末端P1點的軸向電場強度如圖9所示.在發射面的峰值電流密度(對應X射線注量)很低時, 如J0= 0.1 A/cm2, 空間電荷效應極弱, 考慮二次電子發射就會使模擬得到的電場強度峰值增大約0.6倍.增大發射面的峰值電流密度至J0= 5 A/cm2, 空間電荷效應顯著增強, 無二次電子條件下P1處的電場強度發生振蕩.打到腔體末端面的光電子數量在較強的空間電荷限制作用下減少, 但考慮二次電子發射后, J0=5 A/cm2條件下算得的電場強度幅值仍為無二次電子條件下的3倍左右.在金屬腔體中, 為保證導體為等勢體, 腔體的電荷需要重新分布從而影響整個腔體內部的電磁場分布, 二次電子在這里主要是通過增大金屬導體上的電荷數來影響腔體末端的電場強度.P3處的軸向電場強度隨電流密度的變化與圖4中所示腔體外SGEMP在發射面附近的變化規律類似, 這里不再給出.

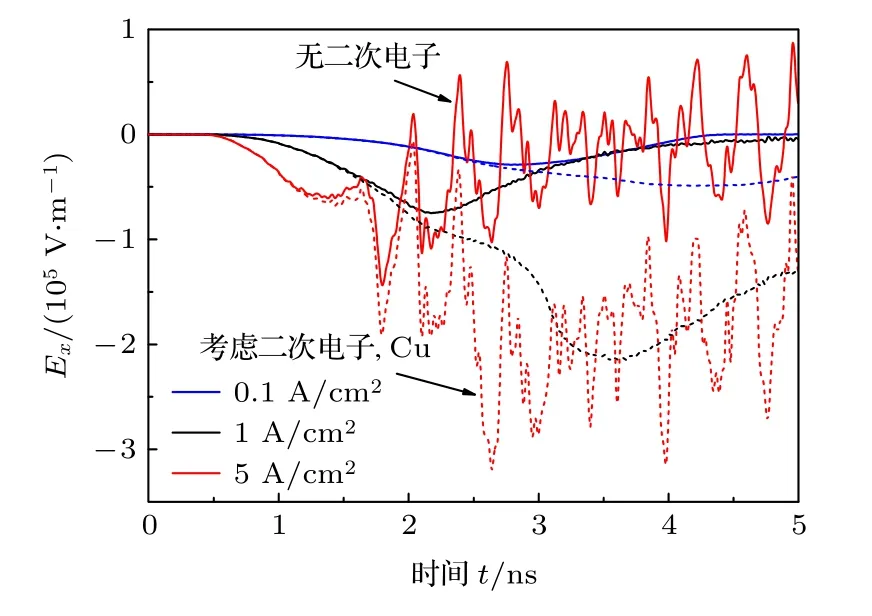
圖9 不同峰值電流密度下, P1位置的軸向電場強度Ex (實線: 未考慮二次電子發射, 虛線: 考慮二次電子發射,E0 = 5 keV)Fig.9.Axial electric field Ex at P1 for different peak current densities (Solid line: not including secondary electrons;dash line: including secondary electrons, E0 = 5 keV).

圖10 給出了不同初始光電子能量E0下, P1處的電場強度(Cu腔體).不同電子能量下, 考慮二次電子發射都會使P1位置算得電場的極值增大一倍以上.這是因為光電子能量越高, 空間電荷效應越弱, 光電子更容易打到末端面, 且其運動速度更快, 所以兩計算模型中電場強度表現出差異的時刻越早, 由5 keV時的1.46 ns提前至50 keV的1.06 ns.而是否考慮二次電子發射條件下, 計算出的Ex1谷值時刻之差也由5 keV的1.41 ns縮短至50 keV的0.46 ns.這是因為測量點P1距金屬腔體右端面仍有一定距離(5 mm), 無二次電子條件下, 電場谷值時刻對應大量光電子到達P1的時刻; 考慮二次電子時, 谷值時刻由向右運動的光電子與向左發射的二次電子共同決定.二次電子的作用又主要由背散射電子體現, 由于高入射電子能量下背散射電子的平均能量更高, 背散射電子由右側端面運動到P1位置所需時間更短, 谷值出現時刻之差也越小.

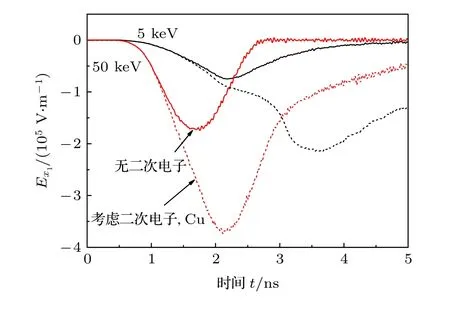
圖10 E0 = 5 keV與E0 = 50 keV條件下, P1位置 的軸向電場強度Ex(J0 = 1 A/cm2)Fig.10.Axial electric field Ex at P1 for E0 = 5 keV and E0 =50 keV (J0 = 1 A/cm2).

4 結 論

為了研究二次電子發射對SGEMP數值模擬結果的影響, 本文較為全面地考慮了電子-金屬相互作用產生二次電子的物理過程, 實現了基于PIC方法的三維非穩態SGEMP數值模擬.針對圓柱腔體外部、內部兩種典型結構下的SGEMP, 計算并比較了不同電流密度、初始光電子能量以及金屬材料條件下的電磁場響應, 主要結論如下:

1)在數值模擬中忽略二次電子發射會導致對電場、磁場強度的低估, 對于非受輻照面, 峰值電場強度會被低估2-3倍, 響應的時間寬度也會被低估10%以上.

2)在各類二次電子中, 背散射電子對SGEMP的影響占主導, 真二次電子對電場強度差異的貢獻約為背散射電子的1/5.構成系統的金屬材料的原子序數越高, 二次電子發射對電磁場響應的影響越大.

3)受結構影響, 對于腔體外SGEMP, 僅有高X射線注量, 空間電荷效應較強時, 二次電子才會對電磁場響應產生影響, 而在較低的輻照注量下, 腔體內SGEMP受二次電子發射的影響就較為顯著.