多源融合導航系統的因子圖算法綜述

羅子巖，陳 帥，王國棟，趙海飛，馬永犇

(1.南京理工大學自動化學院，南京 210094；2.北京航天控制儀器研究所，北京 100039)

0 引言

導航定位技術是現代戰爭中不可或缺的關鍵技術，在精確打擊和協同作戰中發揮著重要作用，同時也在無人駕駛等民用領域廣泛應用。目前，隨著對導航定位性能的要求越來越高以及導航環境的日益惡劣，集成在一起的傳感器種類和數量也不斷增加，導航手段已從單一導航方法發展到多源、全源組合導航系統階段，多傳感器的組合導航系統已經逐漸成為各種復雜環境下長時間高精度導航的主要方式。

在多傳感器數據融合方面，目前采用較多的方法是聯邦Kalman濾波算法。但是，多傳感器數據融合系統往往各個傳感器的頻率不同，誤差特性也不同，傳統的Kalman濾波算法為了保持數據的同步往往需要丟棄一部分測量值，這樣會造成信息的浪費。同時，標準Kalman濾波器只能解決線性問題，而大多數傳感器模型都包含了非線性成分。擴展Kalman濾波算法應用于非線性狀態估計系統中雖然已經得到了學術界認可并被廣泛使用，然而該種方法也帶來了兩個缺點：1)當強非線性時其違背局部線性假設，Taylor展開式中被忽略的高階項帶來大的誤差時，擴展Kalman濾波算法可能會使濾波發散；2)由于在線性化處理時需要用Jacobi矩陣，其繁瑣的計算過程導致該方法實現相對困難。

然而在因子圖框架下，每個傳感器的測量值被編碼成為一個因子，只需在產生測量值時加入組成框架圖，通過對這些連接起來的因子使用Bayes推理來完成數據融合和參數估計。這種方法顯然適用于處理異質異構非周期數據融合問題，具有很高的靈活性，能夠以即插即用的方式配置、組合傳感器，如果有傳感器失效，也可以從因子圖框架中及時刪除。因此在多源組合導航中，因子圖的身影出現得越來越頻繁，其在無人機、自主水下潛器(Autonomous Underwater Vehicle，AUV)、無人駕駛等領域都有相應的應用，并且逐漸出現了各種基于因子圖的改進算法[1]。本文將對因子圖模型理論以及因子圖算法的應用情況進行研究，并展望其發展前景。

1 因子圖模型

將一個具有多變量的全局函數因子分解，得到幾個局部函數的乘積，以此為基礎得到的一個雙向圖叫做因子圖。因子圖是概率圖模型的一種，其不僅可以被用來解決數學概率問題，還能被用來解決人工智能、信號處理、數字通信等其他領域的復雜問題[2]。當處理包含許多變量的全局函數時，通常采用的方法是利用給定函數的因子作為一個局部函數，然后由許多個局部函數的乘積表示全局函數。因子圖便是表示這樣的因式分解的二分圖模型[3]，因子圖模型由變量節點、因子節點以及聯系兩者的邊組成。若包含多變量的全局函數g(x1，x2，…，xn)可被分解為局部函數的乘積，則有

式(1)的因式分解可以使用因子圖表示，且在此雙向圖中，xn表示為一個變形節點，局部函數fj表示為因子節點，Xj表示第j個局部函數fj(·)的自變量點集，再由表示相互關系的邊將因子節點與相應的變量節點聯系起來，下面給出一個具體的例子。

設g(x1，x2，x3，x4，x5)為一個包含五個變量的全局函數，同時該函數還可以被表示為：g(x1，x2，x3，x4，x5) ＝fA(x1，x2)fB(x2，x3，x4)fC(x4，x5)， 則其對應的因子圖如圖1所示。

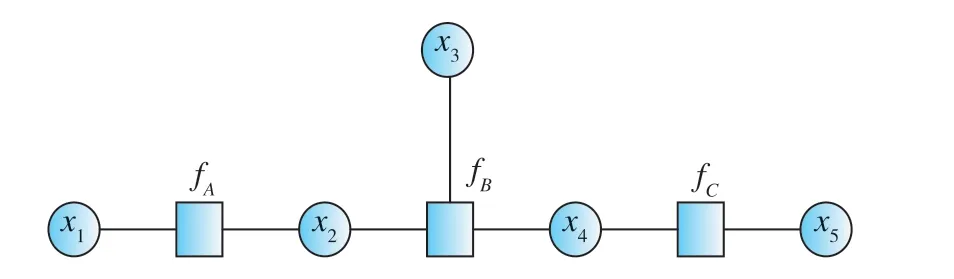
圖1 因子圖結構示意圖Fig.1 Structure diagram of factor graph

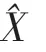
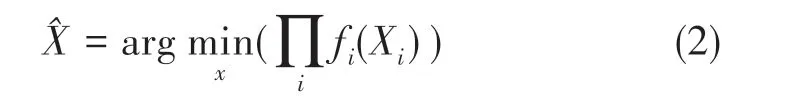
導航系統中，量測函數通常可以根據狀態變量估計預測出傳感器的量測值。而因子節點計算預測的測量值和實際測量值之間的差值通過構建相應函數獲得狀態變量估計，因子節點獲取預測的量測信息和實際量測信息的差值構建相應的指標函數從而獲取代價函數，即

式(3)中，hi(Xi)為與狀態變量有關的量測函數，zi為由傳感器得到的實際測量值，L(·)為代價函數。對于Gauss噪聲分布，L(·)為平方馬氏距離，定義為L(e)＝eT∑－1e，∑通常取量測噪聲方差陣R[4]。

2 基于因子圖的多傳感器信息融合實現

2.1 衛星慣性組合導航實現與因子圖算法可行性分析

文獻[5]以發射慣性系為導航坐標系，選取SINS基本誤差和慣性器件誤差參數構成15維系統狀態向量，在全軟化仿真平臺系統中通過軌跡發生器和衛星信號模擬器依次模擬生成導彈的慣組數據和GPS中頻信號，再對生成的角速率和比力數據進行慣導解算，將GPS中頻信號注入軟件接收機進行導航解算，建立發射慣性坐標系下慣性／衛星松組合導航狀態方程，采用傳統的Kalman濾波算法和因子圖算法進行信息融合。實驗顯示，運用因子圖融合算法的三軸位置均方誤差絕對值均比傳統Kalman濾波算法的誤差略小，較傳統濾波結果有一定的改善。結果表明，因子圖算法可以保證導航系統的正常使用且導航精度可以得到保障。文獻[6]則以慣性衛星緊組合導航為背景對因子圖算法代替Kalman濾波的可行性進行了研究，假設每個衛星就是一個傳感器，提供一組量測信息，同時通過因子圖來表示狀態的遞推與更新。通過Gauss-Newton迭代法求解優化方程，得到最優的狀態修正量，實驗結果同樣證明了因子圖算法的有效性。

2.2 因子圖算法國外研究現狀

2012年，美國Georgia理工學院的Indelman等針對美國國防高級研究計劃局(DARPA)提出的全源定位導航項目并參照Dellaert等的一些平滑定位算法提出了基于因子圖框架的多源導航傳感器融合算法[7-8]。2013年，美國SRI國際公司的Chiu等[1]在美國Georgia理工學院研究的基礎上針對機器人自主導航問題給出了基于因子圖的組合導航系統，該系統包含了57種不同的傳感器。其后，德國Chemnitz工業大學的Lange等[6]將基于因子圖框架的增量平滑多源導航傳感器融合方法應用到裝配有慣性測量單元、光流傳感器和無限反高度表的四旋翼無人機中，并與傳統的擴展Kalman濾波方法進行對比，仿真實驗結果驗證了基于因子圖的增量平滑算法相比傳統濾波算法的優勢。

目前來說，國外的學者對基于因子圖框架的多源數據融合方法已經進行了深入的研究，并且可以較好地處理異步、多速率數據。但是，研究的應用背景多以小場景多動態SLAM問題為主，尚未在實地大場景下進行驗證。

2.3 因子圖算法應用

組合導航系統面臨無人機、導彈、水下潛器等多種使用場景，以及衛星信號被干擾、不同傳感器的使用等各種特殊的情況。因此，因子圖算法被應用于多種使用場景并衍生出基于因子圖算法的各種改進算法。

沒有就算了。村長適時接過話頭。八斗丘補償問題，村委過些天會研究，你不要到處找人說事。特別是不要找那樣專門戳漏洞的什么狗屁記者。

(1)無人機

王慧哲等[9]以民用無人機為背景，結合全源導航需要快速集成并重新配置任意導航傳感器的要求，對全源導航的關鍵技術展開研究，構建了如圖2所示的基于因子圖的多傳感器融合框架，其中涉及的傳感器包括IMU、GPS、氣壓高度計、光流傳感器、磁航向傳感器、星敏感傳感器。

圖2 基于因子圖的多傳感器融合框架Fig.2 Diagram of multi-sensor fusion framework based on factor graph

在接收IMU觀測信息后定義因子節點fIMU，連接tk和tk+1兩個不同時刻的變量節點即導航狀態xk和xk+1， 因子節點IMU可表示為

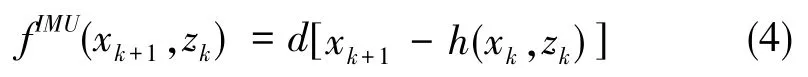
在tl時刻接收到GPS觀測信息后，定義因子節點fGPS

同理，在其他時刻接收到高度計、星敏感器等傳感器觀測信息后，定義相應因子節點拓展因子圖，根據相應的觀測方程和代價函數進行變量節點的狀態更新。實驗以Matlab為平臺實現對飛行器軌跡的設計，模擬不同傳感器的數據輸出以及對文中提出的算法進行仿真驗證。運動軌跡仿真通過抬頭、爬升、平飛、轉彎、傾斜、俯沖等機動動作模擬飛行器真實的飛行狀況，并且設置GPS在500s～1000s內不可用、星敏感器在800s～1200s內不可用、光流傳感器在1300s～1400s內不可用，以模擬飛行過程中的故障情況。仿真結果表明，因子圖算法能對異步異質傳感器的數據進行有效融合，并適應傳感器在運行過程中可用性發生變化的情況。

文獻[10]以無人機MINS／BDS／磁羅盤／氣壓高度表組合導航系統為例構建了因子圖信息融合模型，通過車載跑車試驗采集導航傳感器原始數據進行離線仿真，將因子圖融合算法與分散式聯邦濾波算法進行誤差對比，驗證了因子圖算法作為無人機信息融合方法的可行性，并且該方法在高度定位以及航向角測姿上展現了更高的精度。

針對密集集群無人機的協同導航問題，文獻[11]提出了一種基于因子圖優化的無人機群協同導航方法，結合無人機自身的導航信息和無人機之間的測距信息，將無人機群協同導航信息融合問題轉換成因子圖模型，給出了基于消息迭代策略的因子迭代方法，為每架無人機建立局部因子圖，實現了協同導航信息分布式處理和位置優化。仿真試驗結果表明，所提出的方法可有效提高密集集群等多無人機應用場景下的定位精度。

(2)AUV

對于自主水下潛器(AUV)的水下組合導航信息融合技術，國內外眾多研究學者作了大量的研究，其中的分布式Kalman濾波應用最為廣泛。文獻[12]則針對AUV所在水下復雜多變的環境與任務需求提出了基于因子圖的AUV多傳感組合導航算法，對捷聯慣性導航系統、Doppler計程儀、磁航向儀、地形輔助導航設備進行建模，構建了基于因子圖的信息融合框架。仿真結果同樣表明，因子圖方法能夠連續穩定地輸出較高精度的導航結果，有效實現了慣性導航系統與不同導航傳感器的非等間隔融合，且具有很好的靈活性與擴展性。

文獻[13]則提出了一種基于因子圖的多AUV協同導航定位算法，根據當前時刻AUV的領航與跟航關系構建相應的變量節點、函數節點和因子圖模型。之后，針對因子圖中的消息傳遞形式推導了和積算法，隨后對基于因子圖的多AUV協同導航定位算法進行描述和推導。最后的仿真結果表明，算法可以有效估計出AUV的位置信息，且在弱噪聲情況下的定位準確度要優于擴展Kalman濾波算法。另外，在大規模多AUV協同導航定位系統中增減AUV時只需添加對應的局部因子圖模型，因此因子圖方法具有很好的擴展性。

(3)衛星拒止條件下的應用

目前，幾乎所有軍用和民用系統都依靠基于衛星的組合導航系統來獲取導航定位信息。但衛星信號在復雜環境下容易受到干擾，在室內、地下等環境中衰減嚴重。因此，針對衛星導航在一些特定環境和條件下的局限性，國內外學者均對衛星信號拒止環境下的新導航技術展開了多項研究，基于因子圖的導航技術就包括其中。文獻[14]提出了一種基于因子圖協同定位輔助的單星定位方法，利用多個定位目標之間的高精度測距信息建立協作因子圖，并利用該協作因子圖輔助單星定位系統的定位結果，從而提高定位精度。

文獻[15]定義了IMU、BDS和里程計量測因子后構建了基于因子圖的多傳感器融合框架。在跑車實驗中，令五個時間段內北斗衛星信號丟失，在行駛600s后導航精度依舊可以得到有效保障，衛星拒止環境下可以將剩余傳感器信息快速有效融合，實現了多傳感器的即插即用。

2.4 改進的因子圖算法

當GNSS、OD的測量頻率與系統輸出頻率不同以及存在時延時，文獻[16]構建了如圖3所示的因子圖模型。

上述構建組合導航系統因子圖模型的過程表明，組合導航系統中各傳感器的因子節點在因子圖模型中是相互獨立的、互不影響的。當GNSS突然失效時，只需要抑制GNSS因子節點的繼續添加，便轉換為INS／OD因子圖模型；而當GNSS變為有效時，只需要重新加入GNSS因子節點，便恢復為INS／GNSS／OD因子圖模型。這說明采用因子圖模型描述組合導航問題可以靈活地處理傳感器有效性的動態改變，基于因子圖的組合導航算法具有很強的靈活性和實時性。

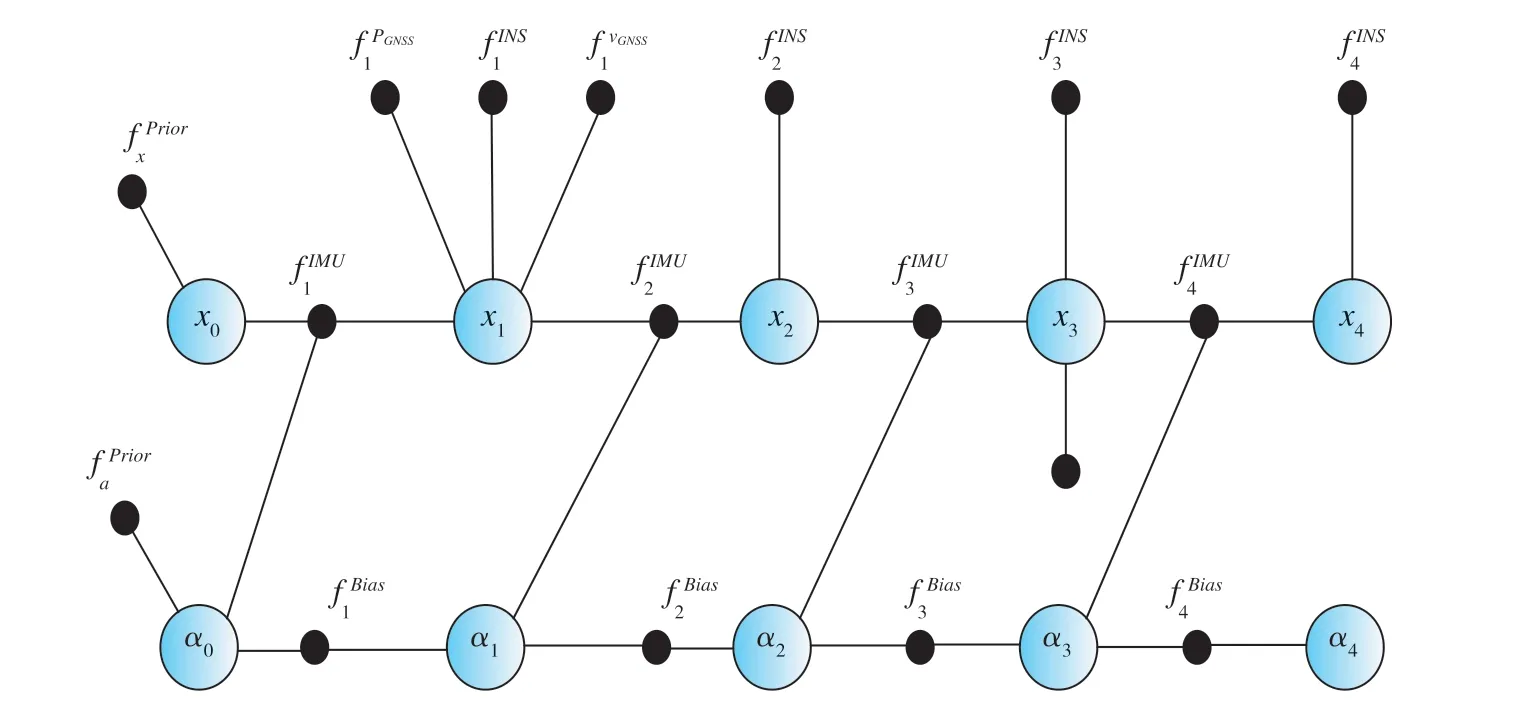
圖3 INS／GNSS／OD存在時延時的因子圖模型Fig.3 Factor graph modelof time delay in the presence of INS／GNSS／OD

文獻[17]提出了如下所示的自適應因子

式(8)中，Φ(Λk)為自適應可信度調節函數，其值為[0，1]之間的標量。從因子圖拓撲網絡角度來看，基于可信度的值，可以啟用或禁用與其關聯的約束邊，從而實現在拓撲中加入或刪除的操作。構建新的自適應因子圖模型，如圖4所示。

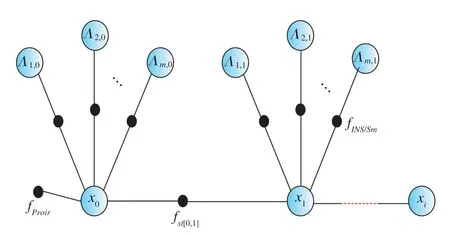
圖4 自適應因子圖模型Fig.4 Diagram of adaptive factor graph model

在仿真實驗中，分別采用傳統因子圖算法和基于可信度的自適應因子圖算法與真實軌跡及慣性／衛星子系統軌跡對比，尤其通過比較衛星拒止區域的定位精度可以看出：基于可信度的自適應因子圖算法能夠自適應調整因子圖拓撲結構，從而保證了復雜動態場景下多源融合導航算法的魯棒性和環境自適應性，提升了自主無人系統跨場景導航模式切換和連續可靠的導航定位能力。

在因子圖算法中，應用Bayes推斷進行狀態量估計的范圍可以是整個因子圖網絡。但是，遍歷估計的方法使得算法在運行過程中的計算量不斷增大，而且最新得到的觀測值對早期變量估計準確性的提高也并不顯著。因此，通過對因子圖的優化范圍加窗，即限定參與優化的因子節點范圍，能夠有效減少算法計算量，提高算法的效率。

滑動窗使得因子圖的全局最優化過程僅發生在最新生成的若干個節點間，它的引入不僅提高了融合算法的估計速度，而且還減少了算法的計算量。

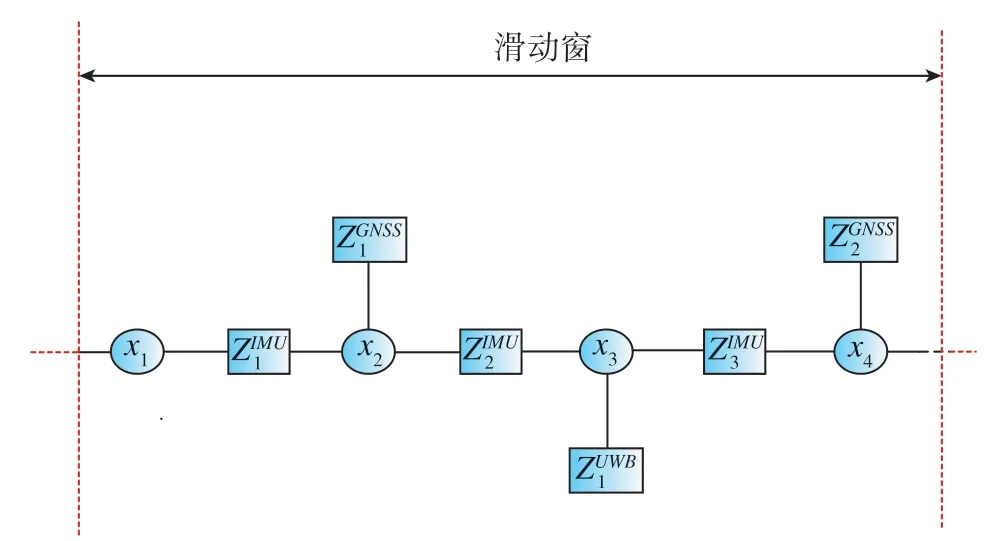
圖5 基于滑動窗口的因子圖模型Fig.5 Diagram of factor graph model based on sliding window

3 總結與展望

如今，單一的導航系統已經不能滿足對導航精度以及抗干擾能力的需求，組合導航技術成為載體導航與定位的主流方法[19]。與單個傳感器信息相比，多種傳感器組合信息顯然能夠提供更精確、更具魯棒性的導航結果[20]。基于因子圖的多傳感器信息融合導航算法可以方便地融合多種傳感器的數據，可以滿足傳感器的即插即用和快速配置。從對因子圖算法的可行性進行分析到其在無人機、水下潛器等上的應用再到多種改進的因子圖算法的提出，國內外已經開展了很多關于因子圖算法的研究，本文也對其進行了一定程度的闡述。但由于理論水平和技術水平有限，目前的研究仍然存在如下的一些改進空間：

1)因子圖算法中，隨著時間的增長，圖中的變量節點也逐漸增加，進行計算的時候，數據維度也逐漸增加，這需要消耗大量的空間資源和時間成本[21]。因此，需要對此進一步進行研究從而提高導航系統的實時性。

2)目前，基于因子圖的多傳感器融合算法大多都是基于松耦合結構的，建立緊耦合融合框架理論上可以提高導航精度，可以作為接下來的一個發展方向。

因子圖算法在即插即用等方面的巨大優勢注定它存在很大的發展空間和實用價值[22]，但迄今為止針對因子圖算法的研究仍只停留在實驗仿真階段，尚未應用于實際系統，同時研究也存在諸多問題，因此仍需要大量的理論工作和工程實踐。