艦載轉運彈鏈用對準系統設計與研究

邱 東，劉 明，游 浪

(湖北航天技術研究院總體設計所，武漢 430040)

0 引言

艦載運轉彈鏈系統采用彈鏈傳遞方式實現導彈的快速發射，為了達到防空功能，系統需要做到快速響應。目前，系統使用的彈載慣組無法在極短時間內進行精確自對準。為達到快速響應的目的，需要增加導彈外部對準系統給導彈提供精確初始基準。對準系統的主體是慣性導航設備與光學測量裝置，具體表現在光學測量裝置測量自身與導彈基準的相對姿態，慣性導航設備實時測量自身的絕對姿態，通過光學測量裝置的測量值、慣性導航設備的姿態信息及其相互間的結構姿態關系聯合解算出導彈基準的實時姿態信息。

因艦載運轉彈鏈結構復雜、存在多種應力環境，為進行對準系統的優化設計，需要進行對應的動力學、熱力學等方面的分析。文獻[1]～文獻[4]提出了基本結構的動力學響應分析方法，文獻[5]～文獻[7]提出了復雜結構的熱力學分析方法，文獻[8]、文獻[9]對艦載導彈裝填系統和發射系統進行了研究，文獻[10]對艦載導彈出筒姿態進行了分析，上述文獻記錄了艦船導彈發射技術的研究，也介紹了相關結構的仿真方法，對導彈出筒姿態也進行了部分分析，但是并未進行艦載導彈快速姿態測量技術和艦載對準系統相關結構仿真技術的研究。

基于運轉彈鏈特征，本文提出并分析了用于對準系統的兩種方案。為進行對準系統的優化設計，一方面以降低成本為目的提出精簡慣性導航設備數量的方法，另一方面對兩種方案的共四種實施途徑進行誤差分析。兩種對準方案均包括偏重測量精度和偏重系統成本的實施途徑，對每種實施途徑分別進行誤差分析。對準系統的輸出誤差包括：單機測量誤差、結構固定誤差、環境因素導致的結構隨機誤差等。其中，單機測量誤差可以通過實驗室精度試驗測量，結構固定誤差可以從標定精度、結構機加工誤差等方面進行分析，環境因素導致的應變引發的結構隨機誤差需要通過系統仿真建模來分析。基于上述分析方法可實現對準系統的優化設計。

1 對準系統方案及優化方法

基于運轉彈鏈特征設計兩種對準方案，分別為視覺方案和自準直方案。系統示意圖如圖1所示，定義Y軸正向為艦艏方向，Y軸負向為艦尾方向；繞X軸旋轉為縱搖，Y軸正向高縱搖角為正；繞Y軸旋轉為橫搖，X軸負向高橫搖角為正；定義繞Z軸角度為航向姿態角，從Z軸正向朝向負向看旋轉逆時針時，航向角為正。

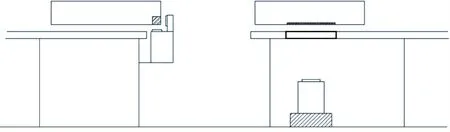
圖1 對系統示意圖Fig.1 Schematic diagram of alignment system

視覺方案的構成包括視覺測量裝置、慣性導航設備、標定板、視覺測量組合安裝基座等，自準直方案的構成包括自準直光學測量裝置、慣性導航設備、六面體鏡組合、自準直組合安裝基座等。其中，自準直光學測量裝置和視覺測量裝置均屬于光學測量裝置，標定板和六面體鏡組合為光學靶標。

托盤上表面為導彈彈箱的安裝基面，通過驅動托盤能夠帶動彈箱在運轉支撐架構上運轉，上述彈箱安裝基面與導彈基準之間的姿態誤差通過結構能夠保證。標定板和六面體鏡組合安裝于托盤不同位置，如圖2所示。

圖2 光學靶標在托盤上的布置Fig.2 Arrangement of optical target on tray

視覺測量裝置通過測量提取標定板上標記點的位置尺寸并解算以得到裝置到標定板間的姿態關系，自準直光學測量裝置通過發射兩個正交軸向的準直光照射六面體鏡組合的兩個鏡面并收取返回光信息以測量自身到六面體鏡組合的姿態關系。因自準直組合視場范圍為角分級，為保證與靶標的相對姿態關系，其安裝基座固連于支撐架構。視覺測量組合的視場角達到±2°，其安裝基座可安裝于艦體內部甲板表面。

慣性導航設備與光學測量設備通過剛性過渡板固連時的結構隨機誤差最小，針對運轉彈鏈特征設計對準系統用過渡板，慣性導航設備、光學測量設備和過渡板構成測量組合。自準直測量組合、視覺測量組合和托盤的位置關系分別如圖3、圖4所示。

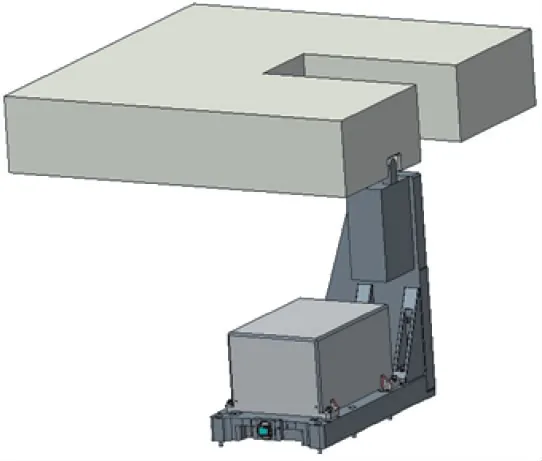
圖3 自準直測量組合和托盤位置關系Fig.3 Position relationship between autocollimation measurement combination and pallet

如圖3所示，A面和B面均連接于運轉支撐架構。如圖4所示，C面固連于甲板。

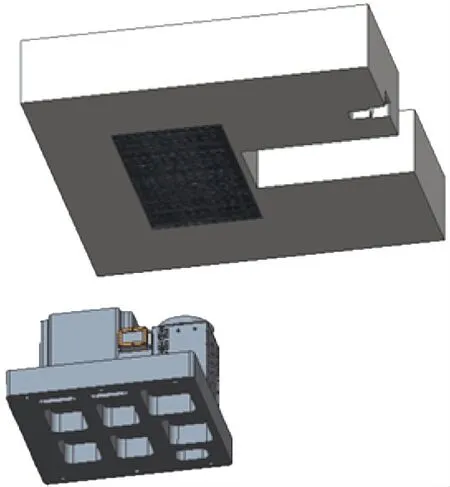
圖4 視覺測量組合和托盤位置關系Fig.4 Position relationship between visual measurement combination and pallet

采用上述方法，結構隨機誤差小，缺點是一臺慣性導航設備只能對應一臺光學測量設備，慣性導航設備利用率低。如果一臺慣性導航設備對應多臺光學測量設備，能降低系統成本，但由于彈鏈尺寸緣故，慣性導航設備與光學測量設備的安裝間距達5m以上，且各自固連于不同部件，結構因素產生的隨機誤差大。因此，在滿足系統精度的情況下，減少慣性導航設備數量的關鍵在于減小結構隨機誤差。

本文先進行系統誤差分析，再基于分析與仿真結果，以保證精度、降低成本為目的進行優化設計。

2 對準系統誤差分析

設定對準系統的測量誤差為系統測量值和導彈彈箱安裝基面實際姿態值之間的差值，將對準系統誤差來源進行具體劃分，如表1所示。

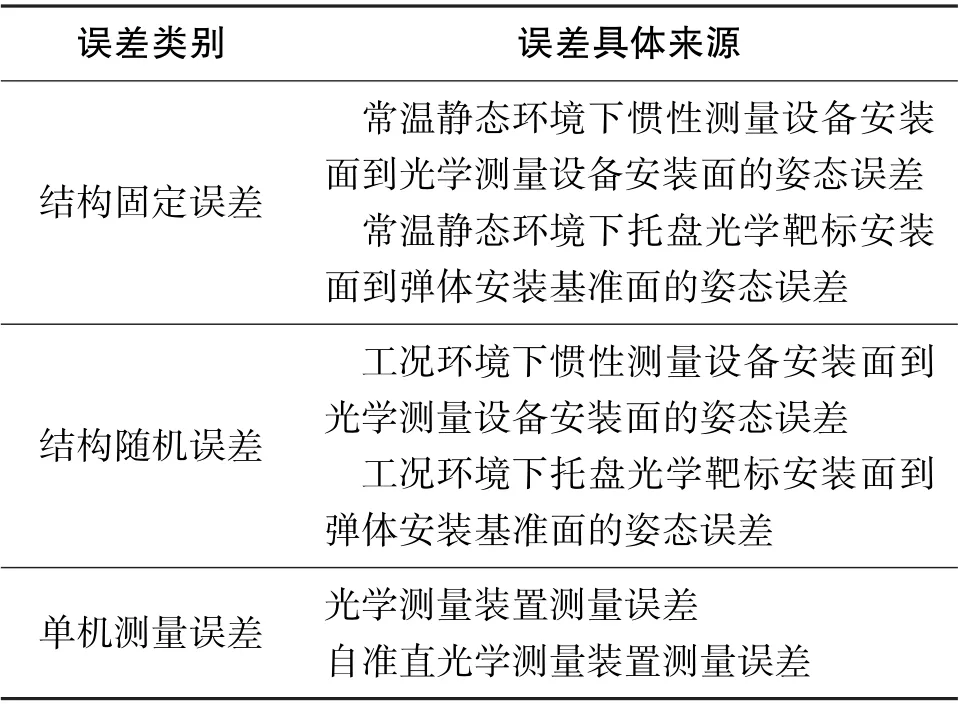
表1 對準系統誤差來源Table 1 Error sources of alignment system

根據試驗測試結果，慣性測量設備因為采用高精度加速度計，測量水平姿態的精度高于測量航向姿態的精度。根據試驗測量數據，其在工況下的測量誤差為90″(MAX，繞Z軸)、60″(MAX，繞X軸和Y軸)；同時，根據試驗測試結果，自準直光學測量裝置的測量誤差為20″(MAX，三方向)，視覺測量裝置的測量誤差為20″(MAX，繞Z軸)、40″(MAX，繞X軸和Y軸)。

下文對結構固定誤差和結構隨機誤差進行詳細分析。

2.1 結構固定誤差分析

(1)標定誤差

光學測量裝置到慣性導航設備之間不存在傳動連接，其相互間的結構固定誤差可以在常溫靜態環境下進行標定，標定值可以用作精度解算的補償量。

在一臺慣性導航設備對應一臺光學測量設備情況下，將慣性導航設備、光學測量設備和安裝基座作為一個組合在實驗室環境下進行標定，標定采用的方法為：通過經緯儀、慣性導航設備自帶航向棱鏡以及實驗室真北基準確定慣性導航設備的航向姿態，通過高精度水平儀確定慣性導航設備的水平姿態；將靶標放置于高精度雙軸轉臺，通過轉臺帶動靶標旋轉。通過光學測量設備讀數、轉臺轉動角度讀數聯合解算出慣性導航設備和光學測量設備的相對姿態。此處，經緯儀的測量誤差約為5″(MAX)，高精度水平儀的測量誤差約為5″(MAX)，慣性導航設備的航向棱鏡及水平儀安裝面到自身理論基準的加工誤差約為7″(MAX)，轉臺標定算法誤差為5″(MAX)，計算上述誤差的和方根，得到的合計誤差為10″(MAX，三軸)。慣性導航設備如果使用高精度加速度計，上述水平儀功能可以通過高精度加速度計實現。

在一臺慣性導航設備對應多臺光學測量設備情況下，由于慣性導航設備和光學測量設備放置于彈鏈不同位置，慣性導航設備和光學測量設備難以作為一個組合，無法在實驗室環境下標定。可使用的標定方法為：通過經緯儀、水平儀等測量慣性導航設備的姿態，方法同上；同時在光學測量設備或其關聯工裝上留航向棱鏡及水平儀安裝接口，通過同類方法測量光學測量設備的姿態，從而求解慣性導航設備和光學測量設備的相對姿態。此處，因為彈鏈內部結構復雜，航向棱鏡通常和北向基準之間存在遮擋，經緯儀測量時需要進行多次光路轉換或者采用中間基準進行基準傳遞，會額外帶來標定誤差。此處，慣性導航設備的航向棱鏡及水平儀安裝面到自身理論基準的加工誤差約為7″(MAX)，經緯儀的測量誤差約為10″(MAX)，高精度水平儀的測量誤差約為5″(MAX)。同時，因為光學測量設備體積小，難以提供經緯儀、水平儀的額外安裝接口，通常使用關聯工裝與光學測量設備固連，負責提供上述安裝接口，此處因加工因素帶來的誤差約為15″(MAX)，合計誤差為20″(MAX，三軸)。

(2)安裝誤差

因為運轉彈鏈托盤數量多，發射時無法嚴格按照既定順序發射，導致對單件托盤進行標定并進行算法補償的難度大，觀測靶標安裝面到托盤彈箱安裝基面的固定誤差，通過結構加工公差進行分析。

光學靶標安裝于托盤下部的安裝基面上，如圖5所示。

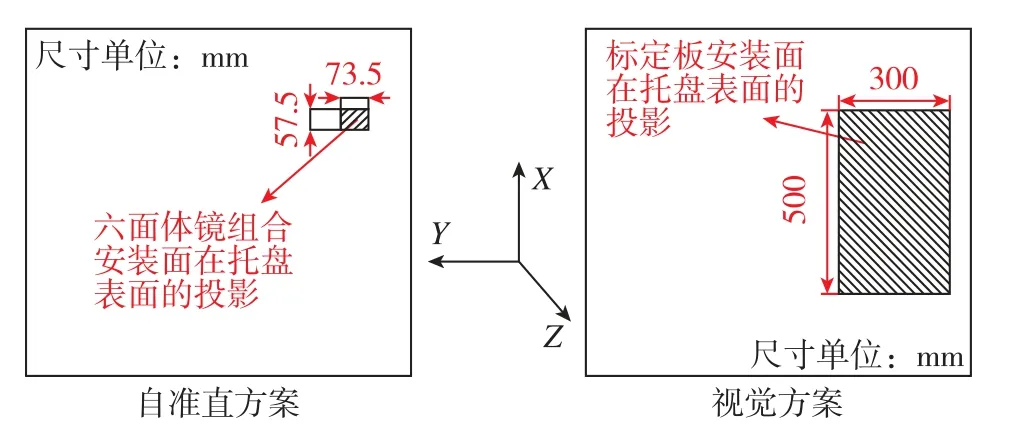
圖5 光學靶標尺寸示意圖Fig.5 Schematic diagram of opticaltarget size

光學靶標相對于托盤基準的安裝姿態依靠其安裝面及安裝靠面保證，基準靠面或者安裝面的形位公差受機加工能力限制，形位公差量級跟其尺寸大小直接相關。視覺方案使用的光學靶標為標定板，安裝面尺寸為300mm×500mm，根據該尺寸，其安裝面與托盤水平基準間的平行度能夠達到0.05mm；安裝靠面設置在安裝面長邊的兩端，長度為500mm，根據該尺寸，其安裝面與托盤航向基準間的平行度也能夠達到0.05mm。在加工極值情況下，標定板與托盤水平基準繞X軸方向的固定誤差達到arctan(0.05mm／300mm)≈35″，標定板與托盤水平基準繞Y軸方向的固定誤差達到arctan(0.05mm／500mm)≈20″，標定板與托盤航向基準繞Z軸方向的固定誤差達到arctan(0.05mm／500mm)≈20″。

自準直方案使用的光學靶標六面體鏡組合安裝面尺寸為57.5mm×73.5mm，根據該尺寸，其安裝面、安裝靠面與托盤基準之間的形位公差能夠達到0.025mm。以同樣方法計算，自準直方案六面體鏡組合到托盤基準間的固定誤差為：70″(MAX，繞Y軸)、90″(MAX，繞X軸)、70″(MAX，繞Z軸)。

基于上述原理，因形位公差導致托盤彈箱安裝面到托盤基準間的固定誤差最大值為30″(MAX，三個方向)。

光學靶標安裝面到彈箱安裝面的固定誤差由上述兩部分加工誤差構成，該處的固定誤差極值由疊加法計算，則視覺方案六面體鏡組合到托盤基準間的固定誤差為：50″(MAX，繞Y軸)、65″(MAX，繞X軸)、50″(MAX，繞Z軸)。自準直方案六面體鏡組合到托盤基準間的固定誤差為：100″(MAX，繞Y軸)、120″(MAX，繞X軸)、100″(MAX，繞Z軸)。

2.2 結構隨機誤差分析

對彈鏈及托盤進行結構仿真分析，以估算慣性導航設備到光學測量設備、光學靶標到彈箱安裝面之間的姿態關系隨機誤差。

按照具體實施狀態進行動力學建模，設定材料參數，根據艦體的實際工況環境要求，設定施載邊界條件：

1)按照表2的條件施加系統搖擺載荷，周期為6s；

2)托盤位于驅動運轉狀態，加載驅動力載荷；

3)全托盤均承載彈箱，帶導彈，即滿載狀態；

4)按照艦船的實際結構特征給模型甲板底部的支撐筋添加約束。

表2 搖擺環境加載條件Table 2 Loading conditions of swing environment

經過仿真運算，截取自準直組合和視覺組合在相關時刻的變形云圖，如圖6～圖9所示。

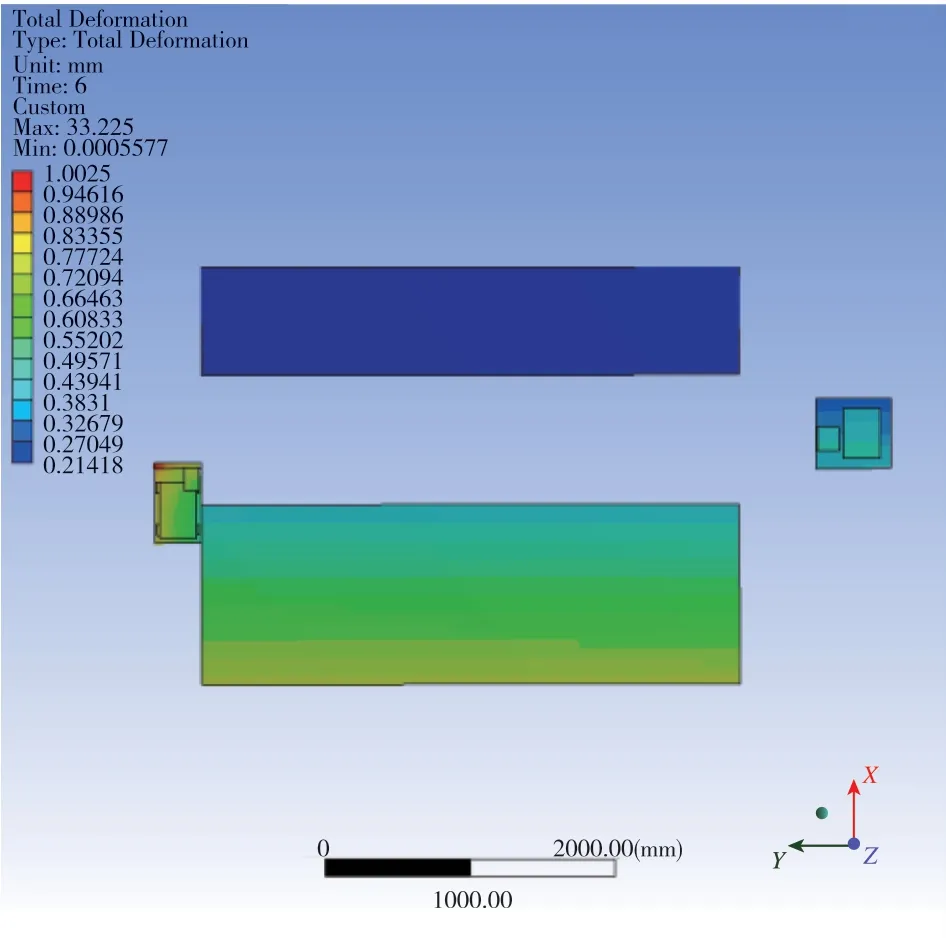
圖6 測量組合位移云圖一(放大50倍，6s)Fig.6 Diagram of measurement combination displacement nephogram I(50 times magnification，6s)

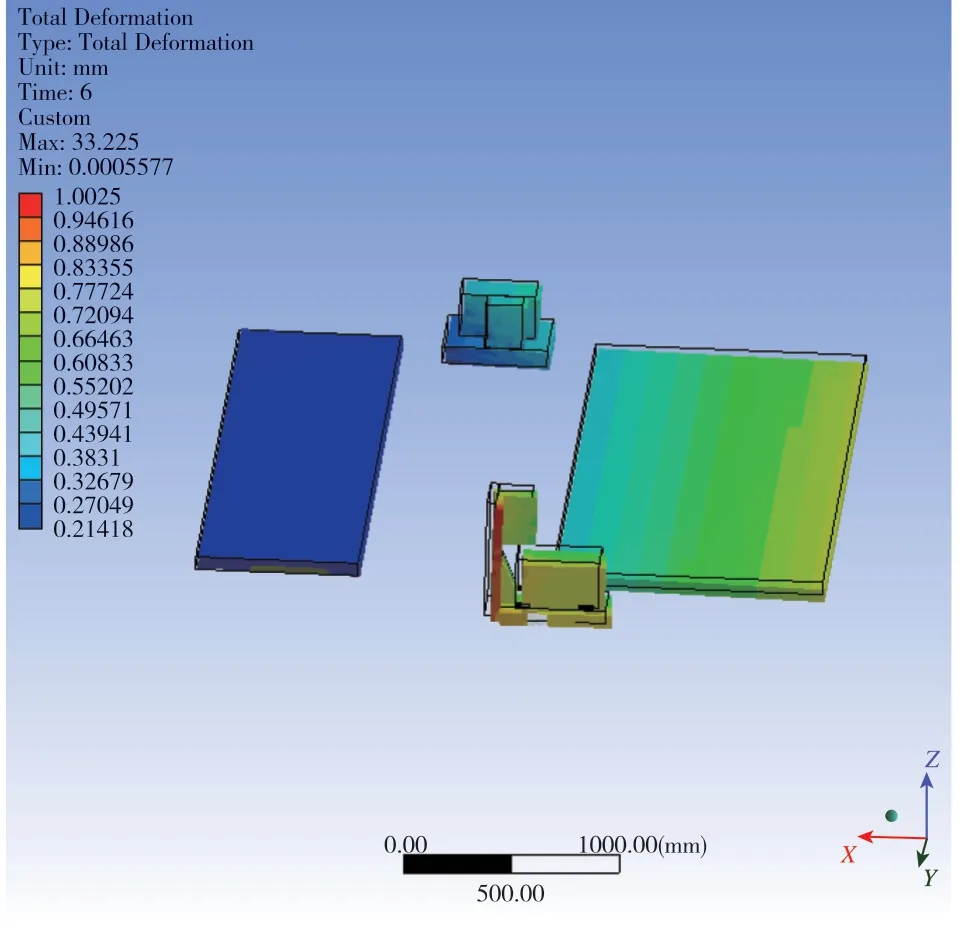
圖7 測量組合位移云圖二(放大50倍，6s)Fig.7 Diagram of measurement combination displacement nephogram II(50 times magnification，6s)

圖8 測量組合位移云圖一(放大50倍，2s)Fig.8 Diagram of measurement combination displacement nephogram I(50 times magnification，2s)

圖9 測量組合位移云圖二(放大50倍，2s)Fig.9 Diagram of measurement combination displacement nephogram II(50 times magnification，2s)

通過仿真計算，搖擺環境下對準系統關鍵部件的姿態角變化結果如表3～表5所示，參考值為橫搖角和縱搖角均為0°、系統僅受重力作用的初始值狀態。

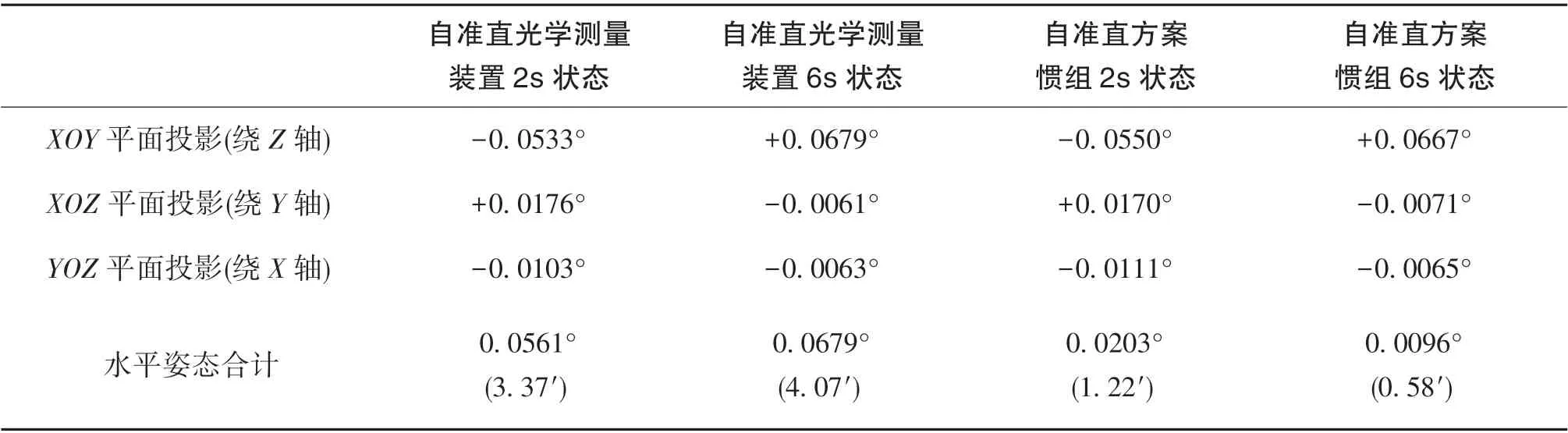
表3 自準直方案搖擺環境仿真計算姿態角變化結果Table 3 Simulation results of attitude angle in rolling environment of autocollimation scheme

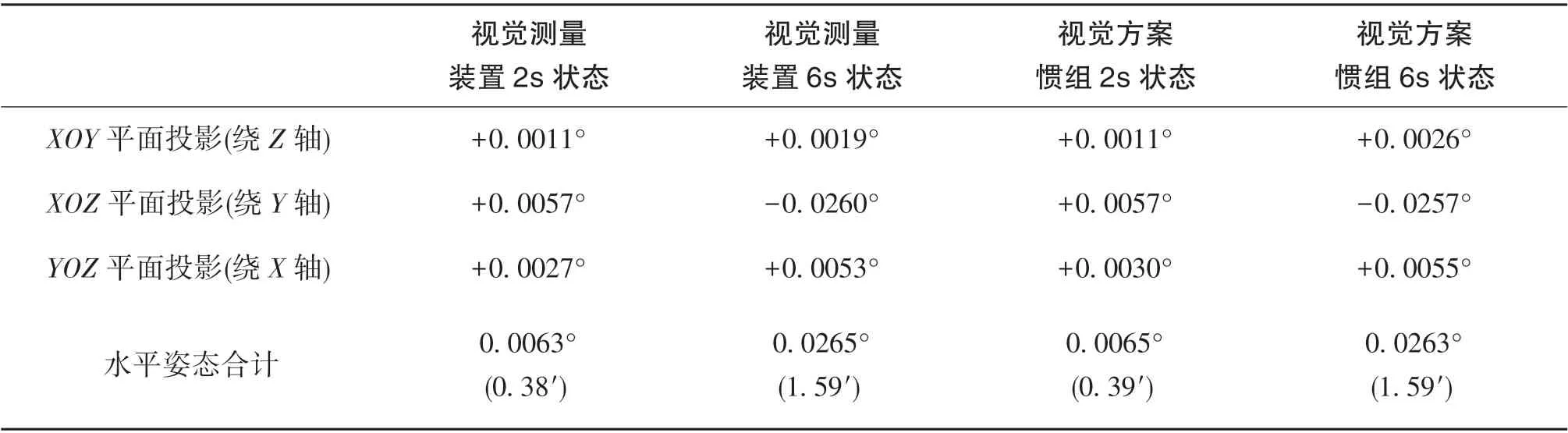
表4 視覺方案搖擺環境仿真計算姿態角變化結果Table 4 Simulation results of attitude angle in swing environment of vision scheme

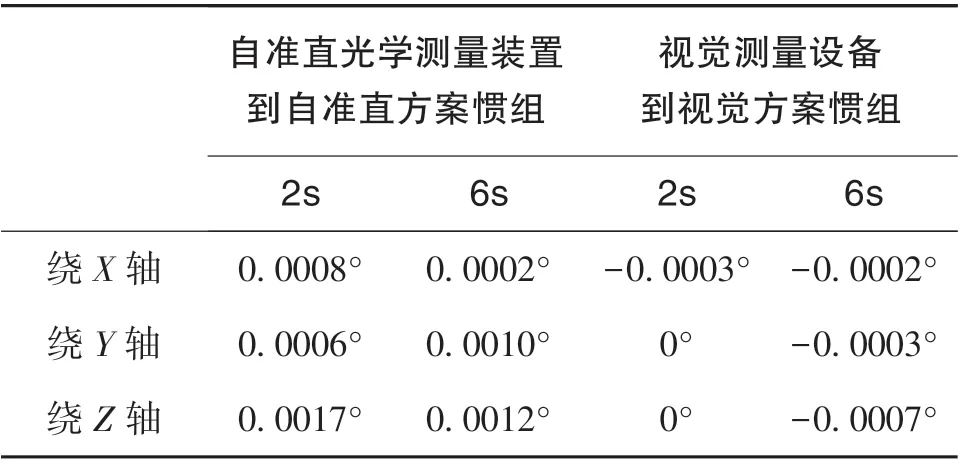
表5 搖擺環境仿真計算姿態角變化結果推算Table 5 Calculation results of attitude angle change in rolling environment

根據上述仿真結果，當光學測量裝置和慣性導航設備安裝于同一個剛性基座時，在搖擺環境下，自準直測量方案的相對姿態變化量均不大于7″(三軸方向)，視覺方案的相對姿態變化量均不大于3″(三軸方向)。

上文已述，因為自準直光學測量設備的視場角和測距原因，其必須和彈鏈固連，以避免托盤靶標超出視場，視覺測量設備因視場角大可以放置于甲板。根據表3和表4的數據，自準直光學測量設備所處的安裝面因彈鏈框架剛度、甲板底部筋條剛度及整體質量分布等因素導致航向姿態變化量較大。在搖擺狀態下，單軸最大姿態變化達到4.07′，在縮減局基數目的情況下不利于保證對準系統精度；而視覺設備放置于甲板，承受彈鏈及甲板的交互作用小，安裝面應變小。

為分析托盤在工況環境下應變導致的隨機誤差對對準系統測量精度帶來的影響，構建分析模型，分析模型包括：托盤、標定板以及作用于托盤上表面的彈箱底部安裝框架。托盤形變的主要來源包括：1)承載彈體、彈箱及自身質量帶來的應力變形；2)托盤內部單機工作產生的熱量引發的熱應力變形。

托盤光學靶標安裝面到托盤彈箱安裝面的姿態變化是重點分析對象，托盤標定板安裝面、六面體鏡組合安裝面的應變云圖分別如圖10、圖11所示。

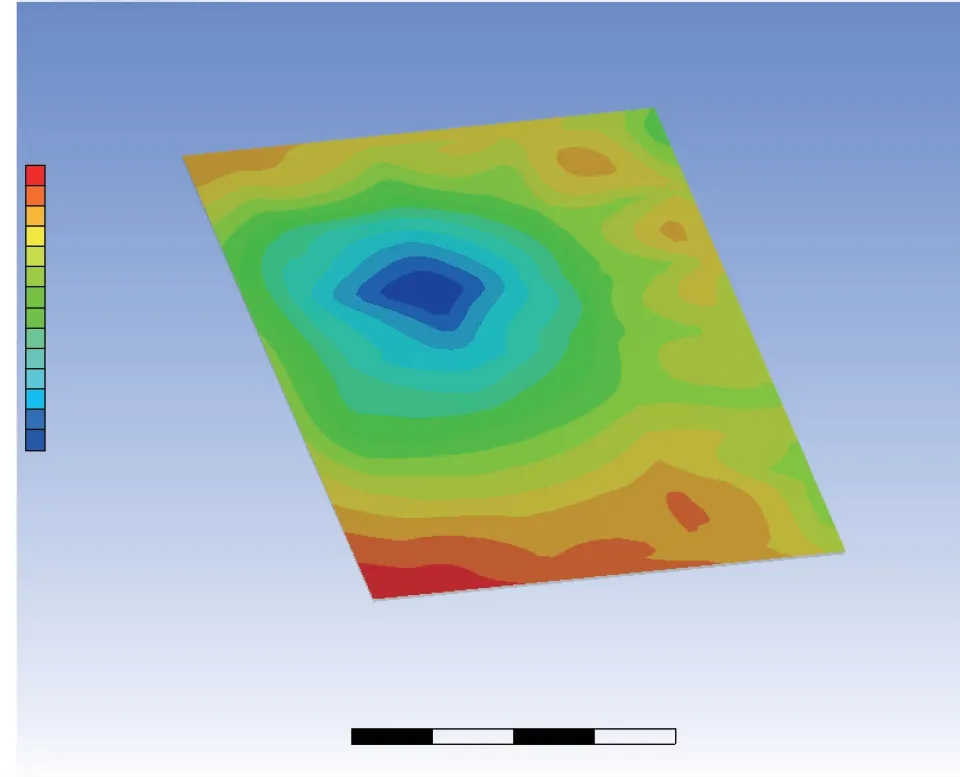
圖10 標定板安裝面應變云圖Fig.10 Deformation nephogram of calibration plate mounting surface

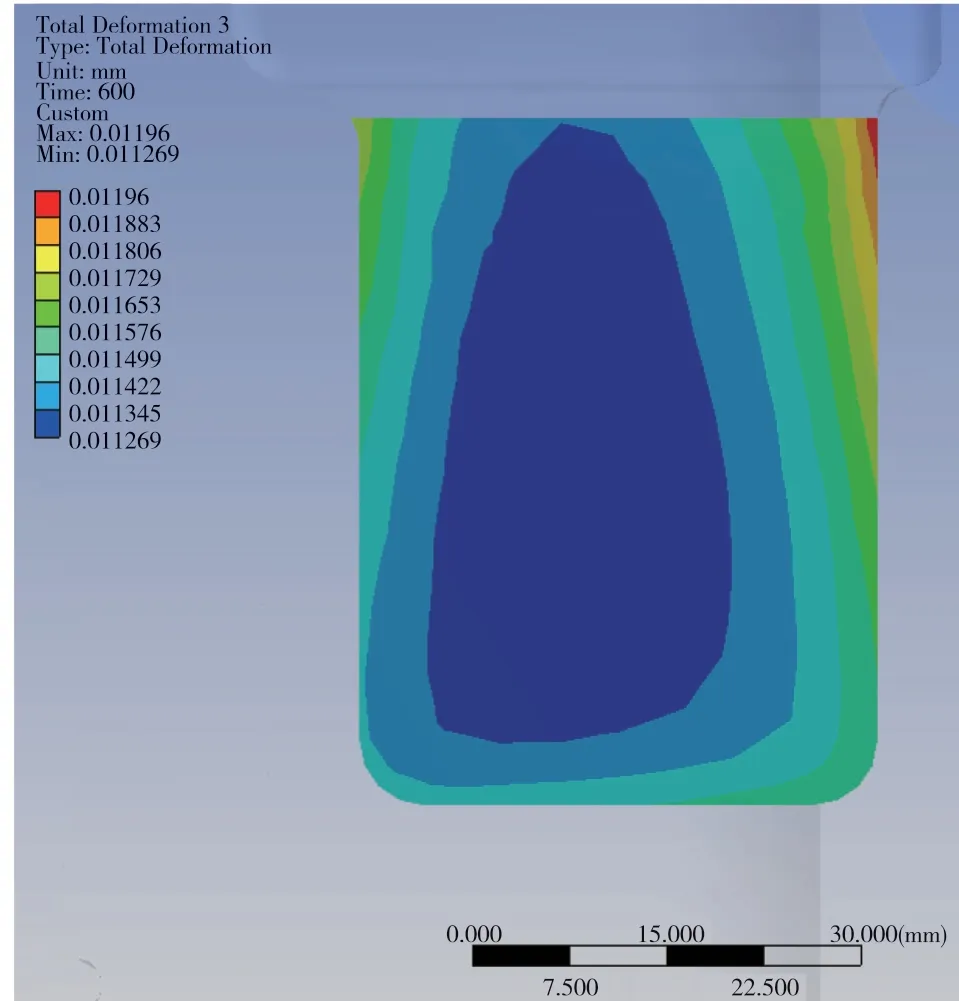
圖11 六面體鏡組合安裝面應變云圖Fig.11 Deformation nephogram of hexahedralmirror combination mounting surface

由圖10和圖11的仿真數據，可計算得到工況環境下光學靶標、彈箱安裝面相對各自初始狀態的姿態變化量。對于每個正交軸，分別計算托盤彈箱安裝面到托盤光學靶標安裝面的隨機姿態誤差，該隨機誤差極值為兩個安裝面相對各自初始姿態繞對應坐標軸姿態變化量的差值。據此原理計算托盤標定板安裝面、六面體鏡組合安裝面及托盤彈箱安裝面三軸方向的姿態變化量，結果如表6所示。

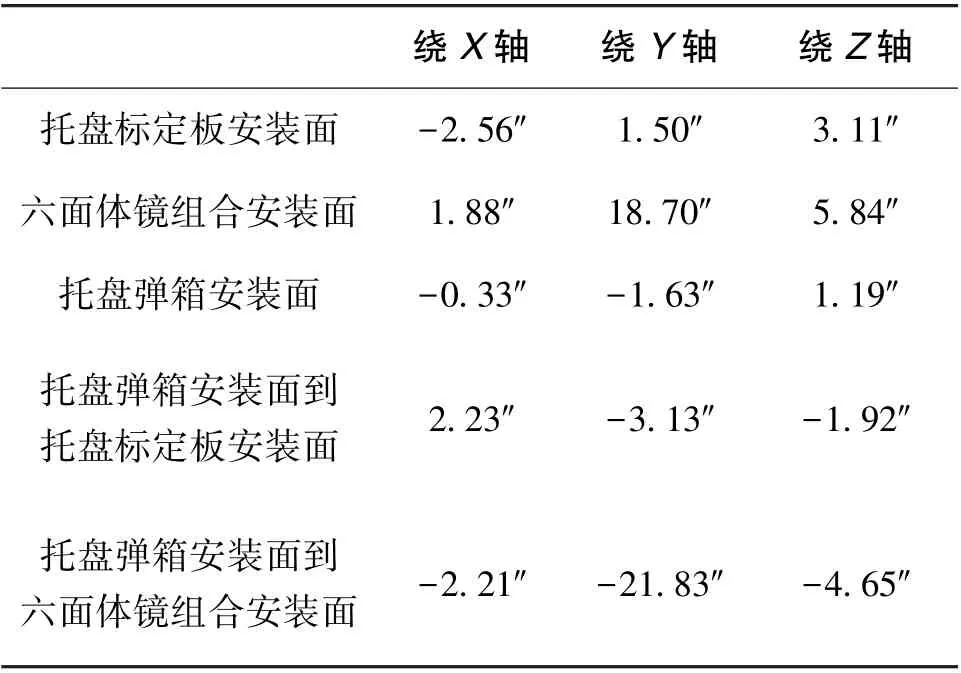
表6 托盤分析模型相關部件姿態角變化計算結果Table 6 Attitude angle change calculation results of the tray analysis modelrelated parts

3 方案優化及結果分析

艦船甲板底部的支撐筋架一般呈陣列布置，相同的彈鏈底部結構具有類似的剛度特性，上文分析的光學測量裝置隨機誤差是多彈鏈中的極值。在此基礎上，將慣性導航設備放置于結構隨機形變小的區域，能夠保證一臺慣性導航設備對應多臺光學測量裝置情況下的系統測量精度。

經過建模分析，甲板結構剛度最好的區域形變量級最小。選取此處位置安裝慣性導航設備，能夠使得其姿態變化量(三個方向)小于15″。

通過上述分析數據計算誤差的和方根，可得到對準系統的測量誤差，如表7所示。

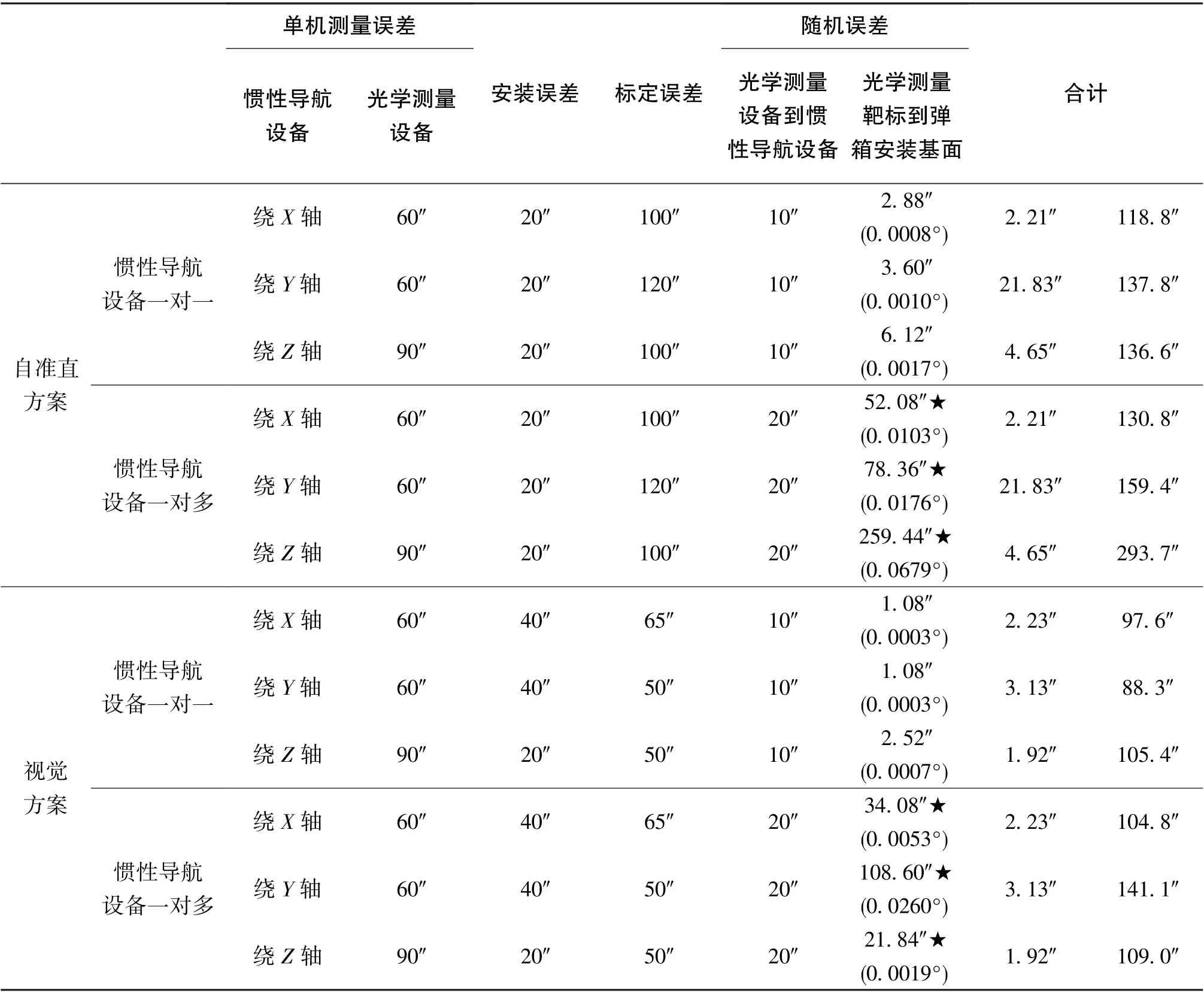
表7 對準系統測量誤差結果(3σ)Table 7 Measurement error results of alignment system

由表7可知，視覺方案的綜合測量精度優于自準直方案。慣性導航設備一對一的情況下，對準系統的最大測量誤差可達到1.8′以內，慣性導航設備一對多的情況下，最大測量誤差為2.5′。

4 結論

本文分析了艦載轉運彈鏈用對準系統的結構特征與測量誤差來源，提出了視覺方案和自準直方案，并分別進行了具體分析。對準系統的誤差來源包括：單機測量誤差、部分結構的加工誤差、標校誤差以及工況下結構應變引發的誤差。通過有限元仿真手段構建系統模型，重點分析了搖擺及溫度變化等工況環境下對準系統各部分的應變情況，分析了因應變引發的結構隨機誤差，再基于誤差來源綜合分析了系統測量總誤差。分析結果表明，在使用足夠慣性導航設備的情況下，對準系統的最大測量誤差可達到1.8′以內。通過仿真分析，將慣性導航設備放置于艦船甲板剛度最佳的區域，能夠有效降低其與光學測量裝置間的結構隨機誤差，達到滿足高精度對準要求的同時縮減慣性導航設備數量的目的，此時對準系統的最大測量誤差為2.5′。