基于時頻組合特征的PSO-SVM手勢識別方法

王亮，張安元，李佳佳，李奇

（長春理工大學 計算機科學技術學院，長春 130022）

表面肌電（sEMG）信號是肌肉收縮過程中多個活躍神經單元發放出的動作電位序列，經過脂肪組織容積導體濾波后，在皮膚表面上的綜合疊加效應［1］。不同的肢體運動對應不同的肌肉收縮方式，相對應動作的sEMG信號特征也會有不同程度的差異［2］。通過提取sEMG信號特征可以確定其對應肌肉的收縮狀態，從而識別出人體所對應的動作模式［3］。在基于sEMG信號的動作模式識別中，只需將電極放置在肌肉表面，無需侵入人體內，再通過藍牙等傳輸設備將電極采集的信號傳輸到終端進行特征提取及動作分類識別。因此，sEMG信號作為一種安全、無創、簡單的肌肉功能檢測手段，在人工智能控制等領域研究中得到越來越廣泛的應用。

sEMG信號的特征提取是手勢識別中的關鍵步驟之一。目前，在識別人體的多種手勢時，通常從時域、頻域、時頻域三方面對信號提取特征，例如，時域特征：過零點數（ZC）、斜率變化數（SSC）、自 回 歸 系 數（AR5、AR4）、絕 對 均 值（MAV）、均方根值（RMS）、方差（VAR）、波形長度（WL）等。頻域特征：平均功率頻率（MPF）、中位頻率（MF）等。時頻域特征：小波系數能量特征（EWC）、小波系數極大值特征（MWC）、小波包系數能量特征（EWPC）、小波包系數極大值特征（MWPC）等，然而這些特征提取方法有各自的優缺點［4］。例如，時域分析較為形象直觀，而頻域分析則更為簡練，分析問題更加深刻，但在時間或頻率上描述sEMG信號時，二者對信號細節表征缺少靈活性，比較單一、片面［5-6］。因此，單純從時域或頻域上描述sEMG信號特征具有一定的局限性。對于時頻域特征分析來說，它雖然兼顧了信號的時域和頻域信息，但此方法用于多手勢識別時，獲取到的動作信息不是十分顯著，所以時頻域特征分析用于多手勢識別時，也有一定的局限［7］。

另外，分類器對于手勢識別也十分重要。對于小樣本數據來說，支持向量機（SVM）分類器通常有著良好的分類性能。但SVM分類器在分類前，需要針對不同樣本數據對分類器參數進行優化。粒子群（PSO）算法在參數優化上有著良好的性能，可以在短時間內找到參數，完成SVM分類器的優化，從而提高分類器的分類性能。

本文提出了基于時頻組合特征和粒子群算法優化支持向量機（PSO-SVM）相結合的手勢識別方法。首先，提取8種時域特征、2種頻域特征、4種時頻域特征，將14種單一特征作為分類特征對手勢sEMG進行分類。然后，將8種時域特征和2種頻域特征進行線性組合，組合的16種時頻組合特征作為新的分類特征對手勢sEMG特征進行分類，來解決單一時域或頻域特征分類準確率不高和時頻域特征對多手勢識別時分類信息不顯著的問題。最后，采用PSO算法優化SVM分類器參數，來解決SVM分類器分類性能的問題，以期來提高手勢識別的準確率。

1 實驗和方法

1.1 數據獲取

本文采用NORAXON公司生產的NORAXONDTS無線肌電采集系統（采樣頻率1 500 Hz）采集sEMG信號，采集了日常生活中具有代表性的八類手勢：（a）掌面向上；（b）掌面向下；（c）內翻；（d）外翻；（e）握拳；（f）展拳；（g）上切；（h）下切。如圖1所示。

圖1 八種手勢動作示意圖

sEMG信號數據來自五名健康大學生（男5名，右利手，平均年齡23.0±1.5歲），均無神經肌肉功能疾病史。所有被試在sEMG信號數據采集前均接受過訓練，掌握了實驗的基本流程和注意事項，能夠正常完成實驗操作流程。實驗前，待測肌肉的皮膚表面需用酒精擦拭干凈，然后將肌電傳感器的雙電極放置在肌肉的肌腹處，兩電極間隔為20 mm［8］。在sEMG信號數據采集過程中，實驗環境應避免電磁干擾，減少人員走動，讓被試的干擾減到最小。被試坐在電腦屏幕前，放松手臂，根據電腦屏幕上的指令，完成相應的動作。

被試每種手勢動作連續執行5次，每次之間停歇5秒。一個動作執行完后，讓手臂處于放松狀態，休息3分鐘，執行下一個手勢動作。然后，肌電采集軟件（NORAXON MR）對采集的手勢sEMG信號進行濾波（20～ 450 Hz的帶通濾波，50 Hz的陷波濾波），最后保存。

1.2 特征提取

本文采用滑動窗口來處理記錄的手勢sEMG信號，并在各窗口中提取手勢sEMG信號特征。每個窗口中，特征向量由五通道的手勢sEMG信號組成。窗口長度為300 ms（450個數據點），步移長度為100 ms（150個數據點）。本文對采集的手勢sEMG信號分別提取8種時域特征、2種頻域特征、4種時頻域特征。

1.2.1 單一特征

本文提取的8種時域特征分別是：過零點數（ZC）、斜率變化數（SSC）、自回歸系數（AR5、AR4）、絕對均值（MAV）、均方根值（RMS）、方差（VAR）、波形長度（WL）。2種頻域特征分別是：平均功率頻率（MPF）、中位頻率（MF）。各特征提取公式如下：

（1）過零點數（ZC）：

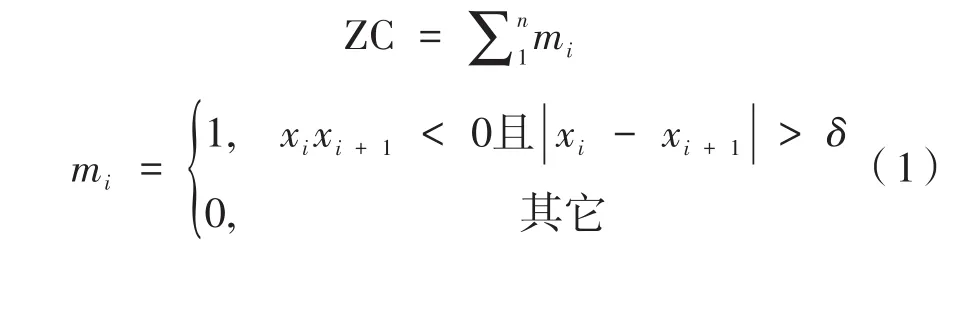
其中，n是窗口中樣本數；xi是窗口中第i個樣本點；δ是閾值。

（2）斜率變化數（SSC）：

其中，n是窗口中樣本數；xi是窗口中第i個樣本點；β是閾值。

（3）自回歸系數（AR5 AR4）：

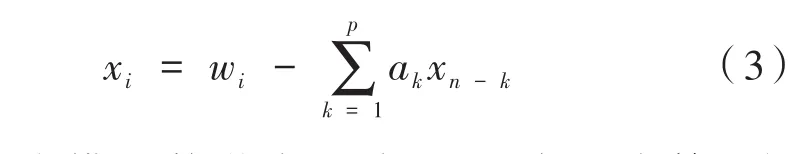
式中，AR為模型數學表達式；xi是窗口中第i個樣本點；wi為噪聲殘差；p是模型階數；ak是模型的第k個系數。當p=4時，所得的系數即為AR4系數，同理p=5時，所得系數為AR5系數。

（4）絕對均值（MAV）：

其中，n是窗口中樣本數；xi是窗口中第i個樣本點。

（5）均方根值（RMS）：

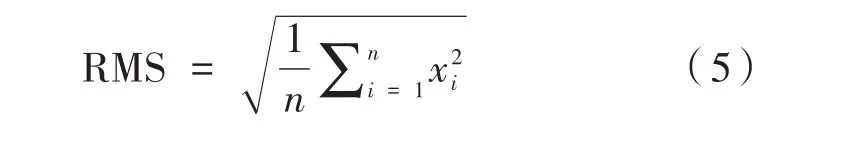
其中，n是窗口中樣本數；xi是窗口中第i個樣本點。

（6）方差（VAR）：

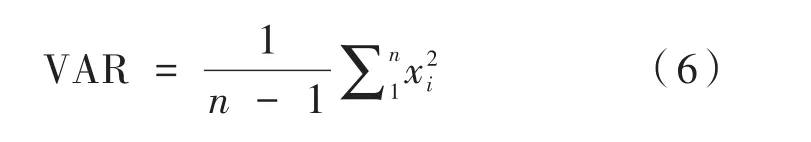
其中，n是窗口中樣本數；xi是窗口中第i個樣本點。

（7）波形長度（WL）：

其中，n是窗口中樣本數；xi是窗口中第i個樣本點。

（8）平均功率頻率（MPF）、中位頻率（MF）：

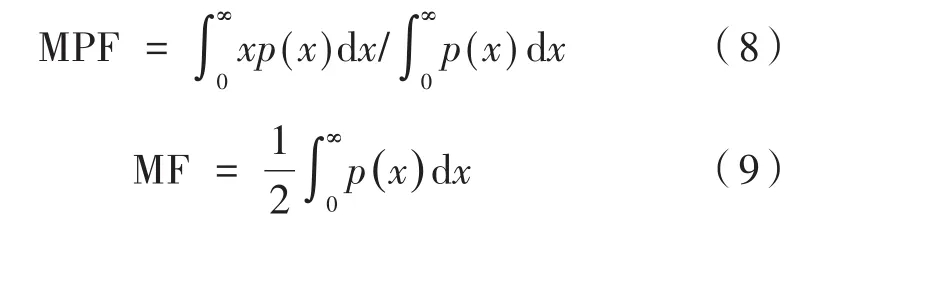
其中，p(x)是信號的功率譜密度函數。

本文提取的4種時頻域特征分別是：小波系數能量特征（EWC）、小波系數極大值特征（MWC）、小波包系數能量特征（EWPC）、小波包系數極大值特征（MWPC）。

小波分解示意圖如圖2所示，其中，S為原始信號，進行 3層小波分解，cA3、cD3、cD2、cD1為小波系數。所以，EWC特征為小波系數cA3、cD3、cD2、cD1的能量值組成的數組。MWC特征為小波系數cA3、cD3、cD2、cD1的極大值組成的數組。

圖2 小波分解示意圖

小波包分解示意圖如圖3所示，其中S為原始信號，進行3層小波包分解，cA31、cD31、cA32、cD32、cA33、cD33、cA34、cD34為小波包系數。所以，EWPC特征為各個頻段小波包系數的能量值組成的數組，MWPC特征為各個頻段小波包系數的極大值組成的數組。

圖3 小波包分解示意圖

1.2.2 時頻組合特征

本文將8種時域特征和2種頻域特征成對線性組合，合成16種時頻組合特征，作為新的手勢識別特征。時頻組合特征的組合過程如下：

假定，時域特征X=(x1,x2,x3,…,xm)，m為時域特征X的維數。頻域特征Y=(y1,y2,y3,…,yn)，n為頻域特征Y的維數。則時頻組合特征Z=(z1,z2,z3,…,zm,zm+1,zm+2,zm+3,…,zm+n)，m+n為 時頻組合特征Z的維數，其中，Z的前m列為時域特征X，Z的后n列為頻域特征Y。

本文提出16種時頻組合特征：ZC-MPF、SSC-MPF、 AR5-MPF、 AR4-MPF、 MAV-MPF、RMS-MPF、VAR-MPF、WL-MPF、ZC-MF、SSCMF、AR5-MF、AR4-MF、MAV-MF、RMS-MF、VAR-MF、WL-MF（注時頻組合特征ZC-MPF是時域特征ZC和頻域特征MPF的組合特征）。

2 PSO算法優化SVM參數

為了讓SVM分類器有更好的分類性能，本文采用PSO算法來優化SVM分類器的懲罰參數C和核函數參數g。

SVM是常見的非線性分類器，它的思想是將輸入的樣本通過非線性變換把樣本映射到高維空間中，在高維空間中找到輸入樣本與輸出樣本之間的非線性關系［9］。即選擇合適的核函數，將樣本投影到高維空間，找到最優的分類超平面，使得樣本與分類平面距離最大。最優超平面即決策函數如下：

其中，ai為訓練樣本的拉格朗日系數；C為懲罰因子；m為閾值；p(xi,x)為徑向基函數的核函數。

其中，g為核函數（徑向基函數）參數。

PSO算法是一種基于全局的優化算法，最優解是通過粒子本身及周圍粒子的經驗進行搜索，并在搜索過程中不斷調整粒子的位置和速度，找到最優解［10］。粒子的位置和速度的迭代更新公式如下：

其中，w是慣性權重；d是空間維數；i∈（1，n）是粒子數；m看是迭代次數；v表示粒子速度；x表示粒子位置；p為最優解；c為學習因子；r為［0，1］區間的隨機數。圖4為PSO算法流程圖。

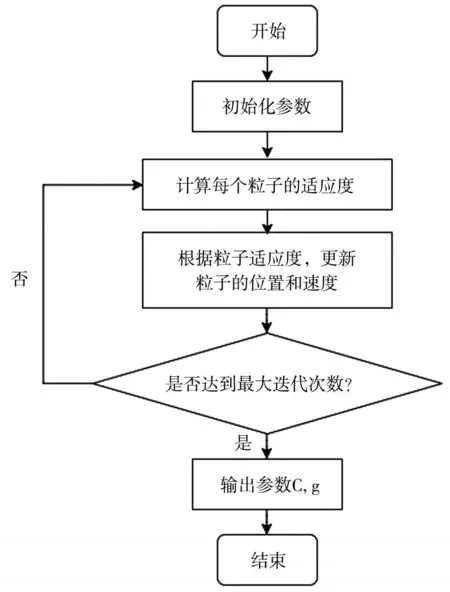
圖4 PSO算法流程圖

（1）初始化參數，通過優化學習因子C和權重系數，確定粒子的權重和位置。

（2）計算粒子的適應度并進行評估。

（3）根據公式（12）更新粒子位置和速度。

（4）看是否滿足終止條件，若不滿足執行步驟（3）；若滿足，則得到最優的參數C和g，并用選擇的參數對SVM分類器進行訓練模型。

實驗中設定PSO的參數如下：學習因子c1=1.5，c2=1.7，粒子迭代的終止次數為100，種群數量為 pop=40［11］。

3 實驗結果及分析

3.1 基于單一特征的手勢識別

本文分別選取上述的8種時域特征、2種頻域特征、4種時頻域特征作為分類特征，采用經PSO優化參數后SVM分類器對8類手勢進行識別，5位被試對8類手勢的平均識別率如表1所示。

由表1可知，對于時域特征而言，基于AR4系數特征的手勢平均識別率最高，為91.54%。基于WL特征的手勢平均識別率次之，為91.49%。基于ZC特征的手勢平均識別率最低，僅為76.23%。對于頻域特征而言，基于MPF特征的手勢平均識別率為88.90%，基于MF特征的手勢平均識別率為78.96%。

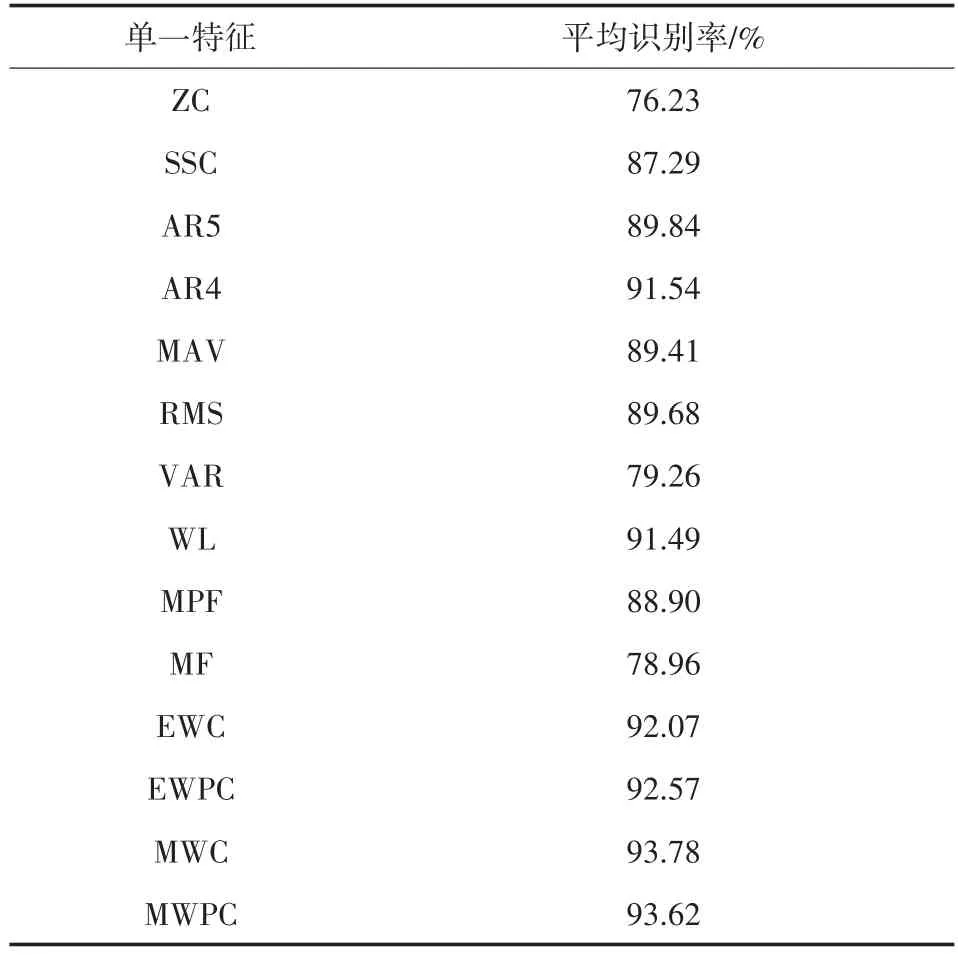
表1 單一特征的手勢平均識別率

可以看出，單一時域特征和單一頻域特征的手勢平均識別率都不高，均未達到95%。因此選取單一時域或頻域特征作為手勢識別的特征進行分類，分類效果并不理想。

對于時頻域特征而言，基于MWC特征的手勢平均識別率最高，為93.78%。基于MWPC特征、EWPC特征的手勢平均識別率次之，分別為93.62%、92.57%。基于EWC特征的手勢平均識別率最低，為92.07%。可以看出，4種時頻域特征的手勢平均識別率均高于單一時域特征和單一頻域特征的手勢平均識別率，但4種時頻域特征的手勢平均識別率均未達到95%。因此，時頻域特征在進行多手勢識別時效果并不顯著。

3.2 基于時頻組合特征的手勢識別

本文選取了16種時頻組合特征作為分類特征。表2顯示的是基于16種時頻組合特征的手勢平均識別率。在16種時頻組合特征的手勢平均識別率中，8種時頻組合特征的手勢平均識別率達到95%。其中基于RMS-MPF時頻組合特征的手勢平均識別率最高，為97.29%。所以時頻組合特征的手勢平均識別率相對于單一特征的手勢平均識別率來說有了比較明顯的提高。

表2 時頻組合特征的手勢平均識別率

由表2知，時域特征與MPF頻域特征的組合特征中，有7種時頻組合特征的平均識別率達到95%，時域特征與MF頻域特征的組合特征中，沒有時頻組合特征的手勢平均識別率達到95%。所以，與MF頻域特征相比，MPF頻域特征和時域特征的組合特征有更好的手勢平均識別率。

為了進一步研究時頻組合特征與單一時域特征和單一頻域特征手勢識別率之間的關系，本文將時頻組合特征與它對應的時域特征和頻域特征分別做配對t檢驗，t檢驗p值如表3所示。由表3可知，表中（除AR5-MPF與AR5、AR4-MPF與AR4、MAV-MF與MAV的p值）時頻組合特征和單一時域特征的所有p值均小于0.05，表明時域特征與頻域特征組合之后，時頻組合特征的手勢識別率有顯著性提高；由表3可知，表中（除ZC-MF、VAR-MF與MF的p值）時頻組合特征和頻域特征的所有p值均小于0.05，表明頻域特征與時域特征組合之后，時頻組合特征的手勢識別率有顯著性提高。所以，除個別特征外，時頻組合特征與它對應的時域特征和頻域特征相比，時頻組合特征有更好的手勢識別率。

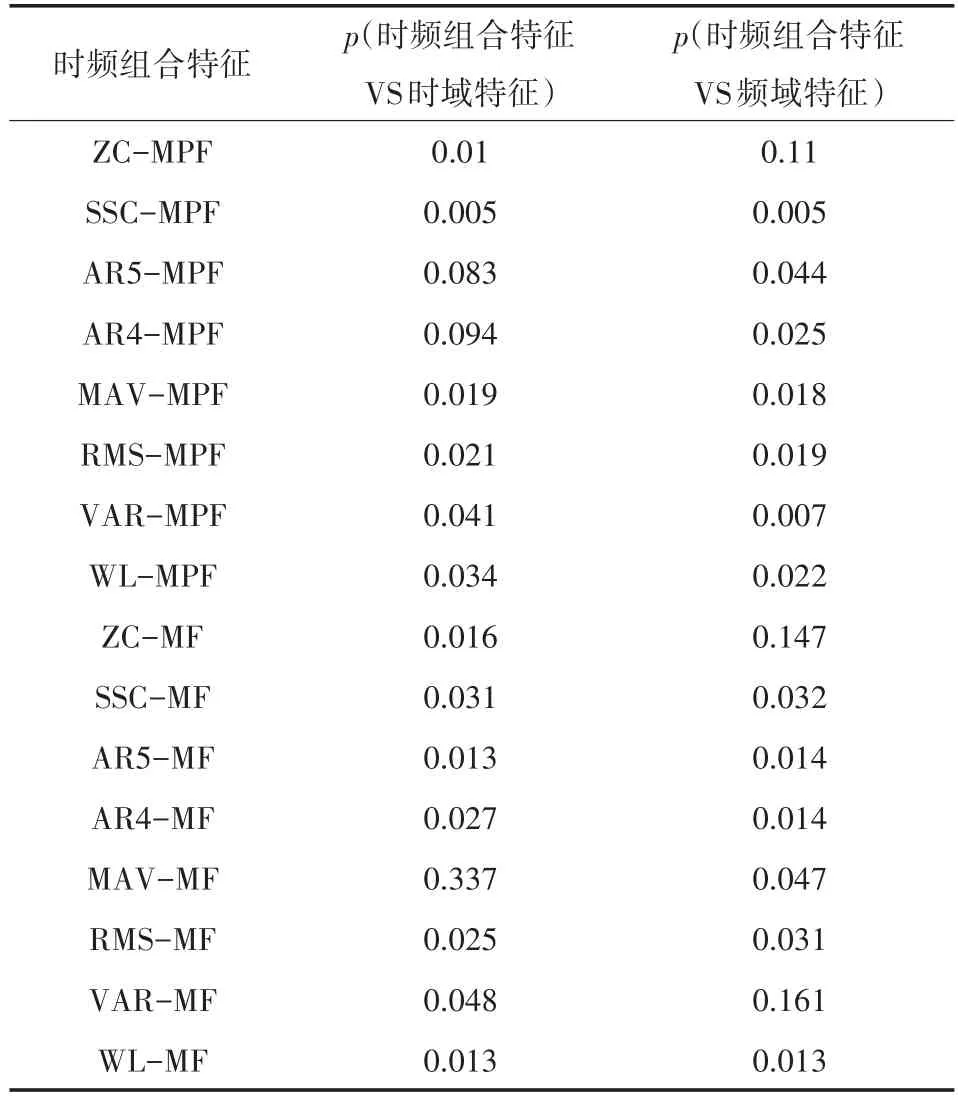
表3 時頻組合特征與它對應的時域特征和頻域特征配對t檢驗的p值

為了進一步研究時頻組合特征與時頻域特征手勢識別率之間的關系，本文將時頻組合特征與時頻域特征做配對t檢驗，t檢驗p值如表4所示。

表4 時頻組合特征與時頻域特征配對t檢驗的p值

由表2和表4可知，時頻組合特征RMS-MPF的手勢平均識別率在16種時頻組合特征手勢平均識別率中最高，與時頻域特征EWC、EWPC的P值為0.02、0.023（p<0.05）。可以看出時頻組合特征RMS-MPF的手勢識別率相對于時頻域特征EWC、EWPC的手勢識別率有顯著性提高。

由表2和表4可知，時頻組合特征RMS-MPF與時頻域特征MWC、MWPC的p值分別為0.065、0.082，雖然它們的p>0.05，但是它們的p值與0.05非常接近，并且p值均小于0.1，所以，可以認為時頻組合特征RMS-MPF的手勢識別率相對于時頻域特征MWC、MWPC的手勢識別率有顯著性提高。所以，可以認為時頻組合特征RMSMPF的手勢識別率相對于時頻域特征的手勢識別率有顯著性提高。

同理，結合表2和表4可發現，時頻組合特征MAV-MPF與RMS-MPF有相似特性。所以，可以認為時頻組合特征MAV-MPF的手勢識別率相對于時頻域特征的手勢識別率有顯著性提高。

4 結論

由于單一特征描述手勢sEMG信號的片面性，所以僅靠單一的時域特征、頻域特征、時頻域特征去識別多種手勢時，往往手勢識別效果不是很理想，為了提高手勢識別的準確率，本文提出了基于時頻組合特征的PSO-SVM手勢識別方法，對8類手勢進行識別分類。結果顯示，時頻組合特征RMS-MPF、MAV-MPF相對于它對應的時域特征、頻域特征有更好的手勢識別率，同時對時頻域特征也有更好的手勢識別率。可以看出，基于時頻組合特征RMS-MPF、MAV-MPF的PSO-SVM識別方法對手勢識別有良好的分類效果。

下一階段的研究內容是采集更多的手勢SEMG信號，對更多的手勢進行分類識別。以及提取更多單一的時域特征、頻域特征、時頻域特征，進行更多時頻組合特征的實驗分析。并且PSO算法在對SVM分類器參數優化時運行耗時較長，還需要不斷的優化PSO算法本身，在不影響算法性能的前提下，極大的縮短PSO算法的運行時間。