光譜自回歸移動(dòng)平均模型的貝葉斯分析方法
胡珍妮,常在斌,崔娟
(西安交通工程學(xué)院,陜西 西安 710300)
自回歸移動(dòng)平均模型(Autoregressive Moving Average,ARMA)的頻譜估計(jì)被認(rèn)為是一些應(yīng)用領(lǐng)域中值得關(guān)注的話題,如工程、計(jì)量經(jīng)濟(jì)學(xué)等。不同的方法已經(jīng)被研究,包括兩個(gè)方面:最優(yōu)方法(如最大似然估計(jì))、基于尤爾-沃克方程的次優(yōu)方法(使用線性方程對(duì)參數(shù)進(jìn)行估計(jì))。
ARMA過(guò)程的估計(jì)方法被廣泛研究,特別是參數(shù)的單獨(dú)估計(jì)[1-2],其中文獻(xiàn)[3-4]使用尤爾-沃克方程估計(jì)AR的過(guò)程參數(shù),然后通過(guò)Durbin方法估計(jì)MA過(guò)程參數(shù)。在這些方法中,應(yīng)用最廣泛的是改進(jìn)的尤爾-沃克方程(Modified Yule-Walker Equations,MYWE)和最小二乘法尤爾-沃克(Least Squares Yule-Walker,LSYW)方法,這些方法為ARMA頻譜估計(jì)提供了相似的結(jié)果。
目前,貝葉斯推理已經(jīng)成功地用于實(shí)際問(wèn)題中。在貝葉斯推理中,未知參數(shù)被認(rèn)為是一個(gè)隨機(jī)變量[5],因此假設(shè)與先驗(yàn)相關(guān)聯(lián)的概率分布是從過(guò)去的數(shù)據(jù)或?qū)<乙庖娭兄付ǖ腫6]。文中的主要目標(biāo)是證明貝葉斯方法估計(jì)參數(shù)ARMA過(guò)程的可行性,通過(guò)比較ARMA模型參數(shù)的估計(jì)值和功率譜的估計(jì)值[7-8],對(duì)經(jīng)典估計(jì)方法和貝葉斯估計(jì)方法進(jìn)行了比較。由簡(jiǎn)單的蒙特卡羅模擬MCMC算法得到了參數(shù)的平均估計(jì)值及其各自的標(biāo)準(zhǔn)偏差。
1 ARMA光譜模型
考慮階數(shù)為(p,q)的ARMA平穩(wěn)隨機(jī)過(guò)程,由以下差分方程式定義:
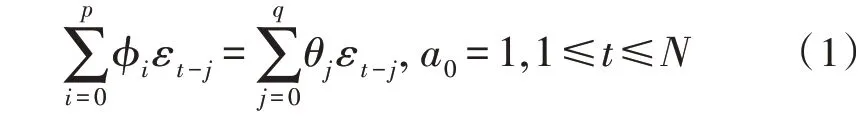
其中,i=0,1,…,p;j=0,1,…,q是過(guò)程參數(shù),εt是均值為零、方差為2的白噪聲。因此,要估計(jì)的參數(shù)向量為:
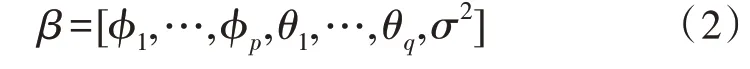
系統(tǒng)函數(shù)在z平面上定義ARMA過(guò)程的功率譜密度為:
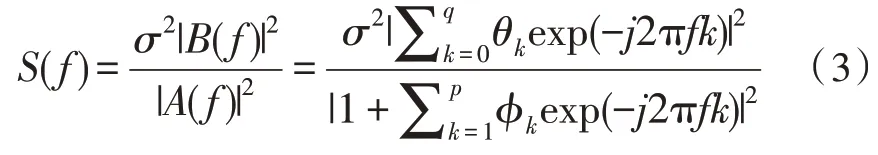
函數(shù)S(f)是自相關(guān)函數(shù)的傅里葉變換,估計(jì)頻率有非負(fù)周期性,周期為1 Hz,頻帶限制在±0.5 Hz。
ARMA光譜估計(jì)的問(wèn)題首先在于選擇合適的模型,以便可以估計(jì)過(guò)程參數(shù)的向量,然后將估計(jì)值替換到光譜密度函數(shù)中。函數(shù)S(f)的這種參數(shù)化是通過(guò)使用參數(shù)β的向量實(shí)現(xiàn)的。
2 使用尤爾-沃克方程的估計(jì)方法
在使用修正的尤爾-沃克方程(MYWE)和最小二乘尤爾-沃克(LSYWS)時(shí),在參數(shù)估計(jì)中使用了多于p個(gè)線性方程。在兩種方法中,都可以對(duì)誤差進(jìn)行加權(quán)以穩(wěn)定方差。此外,這些方法為ARMA頻譜估計(jì)提供了相似的結(jié)果。
2.1 最小二乘尤爾-沃克方法
最小二乘尤爾-沃克方法旨在減少M(fèi)YWE估計(jì)量的方差,提高估計(jì)量的質(zhì)量。已知ARMA過(guò)程的自相關(guān)函數(shù)定義為:
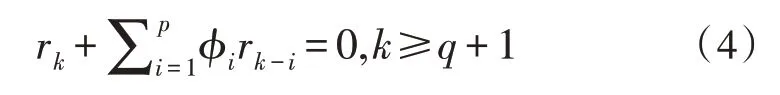
從MYWE出發(fā),首先描述了改進(jìn)的尤爾-沃克方程的最小二乘法,用于估計(jì)AR過(guò)程的參數(shù),因?yàn)锳RMA過(guò)程的尤爾-沃克擴(kuò)展方程可以表示為r=-RΦ。其中,R是展開的自相關(guān)矩陣,r是自相關(guān)向量,可以獲得AR矢量參數(shù)Φ=[φ1,…φp]T的一致估計(jì)。當(dāng)M-q>p時(shí),方程式個(gè)數(shù)多于未知數(shù)個(gè)數(shù),有解。為了估計(jì)自相關(guān)參數(shù),應(yīng)引入一個(gè)大小為(M-q)×1的誤差e,公式為=-Φ+e。其中,和分別對(duì)應(yīng)于r和R的估計(jì)量。
使用無(wú)偏自相關(guān)rk來(lái)估計(jì)r和R是很方便的,使近似誤差的偏差為零。因此,可以使用最小二乘法來(lái)找到使誤差平方和最小的向量,即由此可得,。
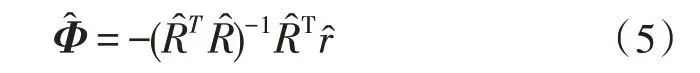
2.2 MA估計(jì)中使用AR濾波器的方法
新的分離估計(jì)方法包括利用Durbin方法的MA參數(shù)估計(jì)[9-10]對(duì)信號(hào)xt進(jìn)行新的AR濾波,從而確定一個(gè)新的信號(hào),如圖1所示,表達(dá)式為。
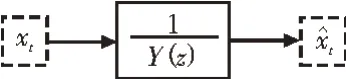
圖1 AR濾波器濾波
在圖1中,1/Y(z)是系統(tǒng)傳遞函數(shù),并且,此過(guò)程類似于重復(fù)Durbin方法的第二步,這是獨(dú)立估算方法的關(guān)鍵思想。
已知,AR(∞)過(guò)程可以作為MA過(guò)程的一種方法。在該方法中,使用新的信號(hào)估計(jì)值xt通過(guò)LSYW方法獲得新的AR估計(jì)值,然后通過(guò)Durbin方法確定新的MA估計(jì)值[11]。提出方法的關(guān)鍵思想是從AR濾波中得到一個(gè)新信號(hào),當(dāng)ARMA過(guò)程的參數(shù)被重新估計(jì)時(shí),它將提供更好的估計(jì)。
3 貝葉斯估計(jì)
在貝葉斯框架中,推理是基于參數(shù)β的后驗(yàn)分布,表示為p(β|x),進(jìn)而用于涉及到?jīng)Q策的推理和決策。后驗(yàn)分布p(β|x)是從先驗(yàn)分布f(β)提供的信息和數(shù)據(jù)通過(guò)似然L(β|x)提供的信息組合中得到的。因此,利用貝葉斯定理,給出了后驗(yàn)分布:
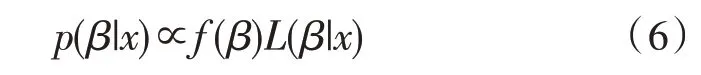
先驗(yàn)分布表示實(shí)驗(yàn)運(yùn)行前有關(guān)參數(shù)β的不確定狀態(tài),后驗(yàn)分布描述觀察到數(shù)據(jù)x后對(duì)參數(shù)β的更新信息。
對(duì)于一個(gè)ARMA(p,q)模型,需要估計(jì)參數(shù)β和σ,其中β=(φ1,…,φp,θ1,…,θq)。在給定矢量參數(shù)(β,σ)的情況下,針對(duì)觀察值X的似然函數(shù)可以寫成:
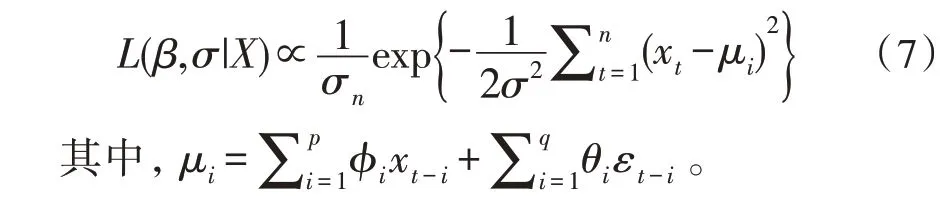
上述似然結(jié)合先驗(yàn)分布,得到的后驗(yàn)分布為:
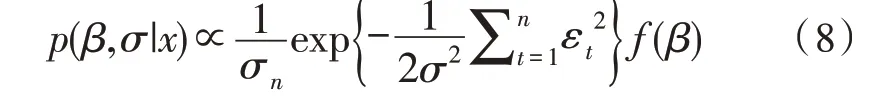
對(duì)于變量xi-p,i=1,2,…,p,誤差項(xiàng)為εi-q,i=1,2,…,q。
為了進(jìn)一步進(jìn)行貝葉斯分析,有必要在參數(shù)空間上指定先驗(yàn)分布。根據(jù)所有當(dāng)前可用的信息,可以使用不同的先驗(yàn)分布。如果研究參數(shù)的先驗(yàn)信息不可用或不存在[12-14],則初始參數(shù)的不確定性可以用非信息先驗(yàn)分布來(lái)量化。因此,對(duì)于ARMA系數(shù),可以將均勻分布用作先驗(yàn)分布。假設(shè)一個(gè)先驗(yàn)條件,即β的分量是獨(dú)立的,則β的總體先驗(yàn)是其組件的先驗(yàn)乘積。因此,β和σ2的聯(lián)合先驗(yàn)分布具有以下形式:
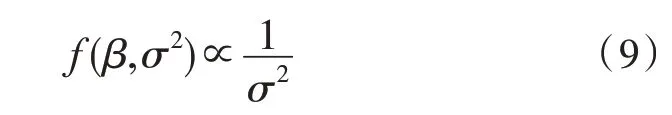
其中,-∞<β<∞和0<σ2<∞。
也可以考慮其他先驗(yàn)規(guī)范作為β分量的獨(dú)立信息正態(tài)分布,即βj~N(μ,),j=1,…,k,均值μ和方差指定了信息先驗(yàn)作為參數(shù)σ2的逆Gamma分布,即σ2~I(xiàn)G(aσ,bσ)的超參數(shù)aσ和bσ已知。因此,β和σ2的聯(lián)合先驗(yàn)將為f(β,σ2)∝f(β)f(σ2)。
為了從模型中獲得每個(gè)參數(shù)的邊際后驗(yàn)分布,需要解決涉及聯(lián)合后驗(yàn)密度的積分,這些積分在解析上不易處理,并且標(biāo)準(zhǔn)積分逼近的效果不佳。在這種情況下,使用馬爾可夫鏈蒙特卡羅(MCMC)方法進(jìn)行貝葉斯后驗(yàn)推理。具體而言,可以運(yùn)行一種算法來(lái)模擬從后驗(yàn)分布中提取的長(zhǎng)鏈,并基于從樣本中計(jì)算出的參數(shù)或參數(shù)函數(shù)的后驗(yàn)總結(jié)進(jìn)行推斷。MCMC本質(zhì)上是使用馬爾可夫鏈的蒙特卡羅積分。
假設(shè)在時(shí)間t處,首先從提議分布q(η|γt)中對(duì)候選點(diǎn)η進(jìn)行采樣來(lái)選擇γt+1,接受候選η的概率為:
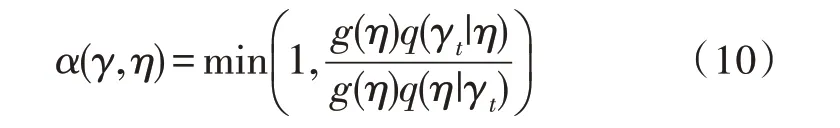
如果候選點(diǎn)被接受,則下一狀態(tài)變?yōu)棣胻+1=η。如果拒絕,則γt+1=γt且鏈條不移動(dòng)。從MCMC算法獲取β每個(gè)分量的隨機(jī)樣本后,重要的是研究諸如收斂和混合等問(wèn)題,以確定該樣本是否可以被合理地視為目標(biāo)后驗(yàn)分布的一組隨機(jī)實(shí)現(xiàn)。除了正式程序外,查看邊際跡線圖是檢查輸出的最簡(jiǎn)單方法。這樣,鏈的所有值都具有由均衡分布給出的邊際分布。
4 數(shù)值圖示
下面描述蒙特卡羅模擬,以便獲得與每個(gè)ARMA流程相對(duì)應(yīng)的參數(shù)和頻譜功率密度的估計(jì)。仿真和程序在Matlab中實(shí)現(xiàn)。
模擬中使用的方法是改進(jìn)的尤爾-沃克方程MYWE、最小二乘改進(jìn)的尤爾-沃克方程(LSYW)、具有AR濾波的最小二乘尤爾-沃克方程(LSYWSAR)、最大似然估計(jì)器(MLE)、考慮非信息先驗(yàn)和獨(dú)立正態(tài)先驗(yàn)參數(shù)的貝葉斯估計(jì)器。
為了評(píng)估這些方法的性能,從相同的種子中生成隨機(jī)數(shù)據(jù),并隨序列的變化而變化,i=1,…,B,B是每次模擬中的重復(fù)次數(shù)。使用N=256個(gè)觀測(cè)值和B=30次重復(fù)進(jìn)行此操作。從均值等于零且方差等于1的標(biāo)準(zhǔn)高斯分布(白噪聲)生成隨機(jī)數(shù),然后生成過(guò)程ARMA的信號(hào)。
改進(jìn)的協(xié)方差是Durbin方法的標(biāo)準(zhǔn),選擇較大的AR過(guò)程階數(shù),并根據(jù)要分析的光譜特征選擇了方程數(shù)M。另一方面,對(duì)于極點(diǎn)遠(yuǎn)離單位圓的頻譜,M取一個(gè)小數(shù),它的一個(gè)極點(diǎn)靠近單位圓,另一極點(diǎn)遠(yuǎn)離單位圓。
在第一個(gè)示例中,使用ARMA(4,2)模型,其中M=10,L=85,N=256;在第二個(gè)示例中,使用ARMA(4,4)模型,其中M=20,L=125,N=256。
示例1 ARMA(4,2)模型
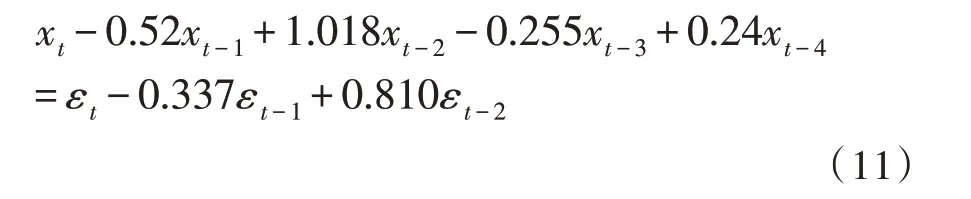
示例2 ARMA(4,4)模型

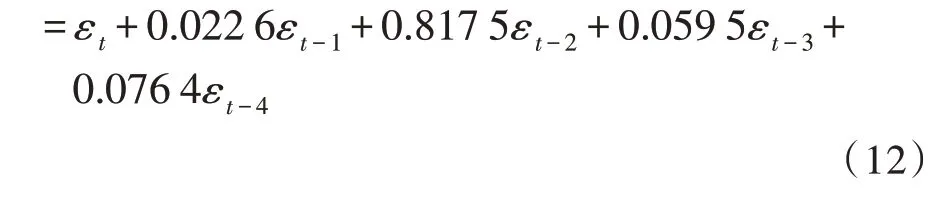
首先,利用示例1的數(shù)據(jù)擬合ARMA(4,2)模型,對(duì)經(jīng)典方法進(jìn)行比較分析,LSYWS方法相比其他方法提供了估計(jì)參數(shù)的最佳平均值,但與AR模型的LSYW方法相比,變異性稍大。LSYW方法產(chǎn)生中間估計(jì)值,但性能優(yōu)于MYWE和MLE方法。這些事實(shí)可以通過(guò)圖2(a)~2(d)中頻譜功率的平均估計(jì)來(lái)觀察,這表明LSYWS方法提供了最佳估計(jì)。將文中研究的經(jīng)典貝葉斯方法與非信息性先驗(yàn)貝葉斯方法進(jìn)行比較發(fā)現(xiàn),兩種貝葉斯方法的參數(shù)估計(jì)值均與LSYWS方法相似,但變異性較小(參見圖2(e)、2(f))。圖2中,虛線是理論值,實(shí)線是估計(jì)值的平均值。
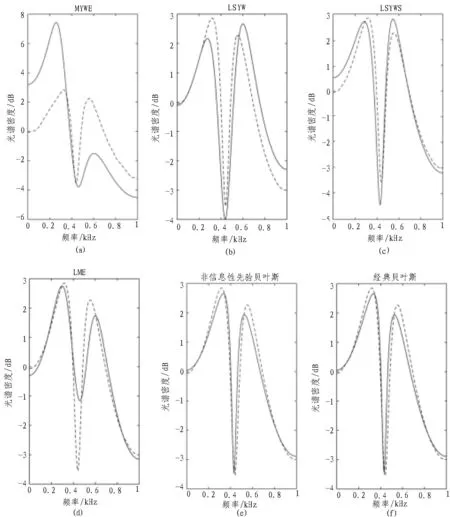
圖2 光譜密度與頻率之間的關(guān)系(ARMA(4,2)模型)
通過(guò)使用非信息性先驗(yàn),獲得了比經(jīng)典先驗(yàn)算法更好的估計(jì),這是由于LME給出的平均先驗(yàn)不能產(chǎn)生如此好的結(jié)果。應(yīng)用于ARMA(4,4)模型的估計(jì)方法MEYW、LSYW、LSYWS和MLE的結(jié)果見圖3。在這種情況下,所有考慮方法的參數(shù)平均估計(jì)值近似相等,只是平均估計(jì)值的標(biāo)準(zhǔn)偏差顯示出與貝葉斯標(biāo)準(zhǔn)偏差之間的差異[15-16]。非信息性先驗(yàn)下的標(biāo)準(zhǔn)差比其他方法的值小,但略小于MLE法得到的標(biāo)準(zhǔn)差,該分析還可以通過(guò)功率譜估計(jì)值的曲線來(lái)確認(rèn)。在這種情況下,這種相似性可能是由于ARMA(4,4)具有穩(wěn)定的功率譜,并且比以前的情況要估計(jì)更多的參數(shù)。
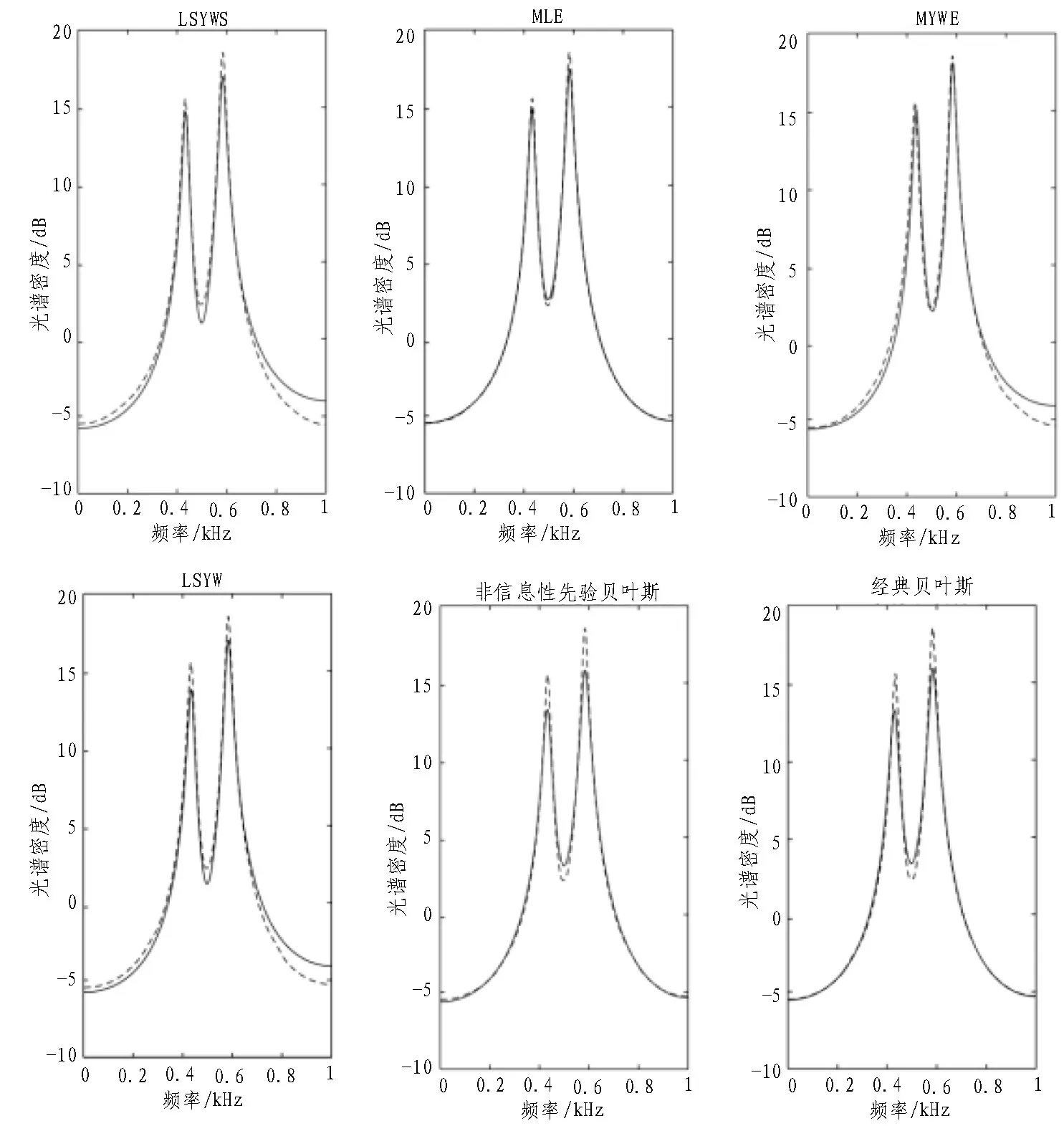
圖3 光譜密度與頻率之間的關(guān)系(ARMA(4,4)模型)
5 結(jié)論
文中通過(guò)使用非信息先驗(yàn)分布估計(jì)ARMA模型的密度譜來(lái)描述貝葉斯方法[17-18]。將該貝葉斯方法與非貝葉斯方法——LSYWS方法和LSYW進(jìn)行了比較,二者均基于尤爾-沃克方程。引入了兩個(gè)具有不同順序的ARMA模型,以說(shuō)明所建議的方法并檢查其性能。該研究表明,考慮ARMA(4,2)模型,貝葉斯方法比其他方法產(chǎn)生的估計(jì)值更準(zhǔn)確。對(duì)于不太穩(wěn)定的ARMA模型,貝葉斯方法是合理的,并且可以選擇任何一種方法來(lái)獲得更穩(wěn)定的功率譜。與其他方法相比,貝葉斯方法提供了適用于任意階次ARMA模型的光譜的最佳擬合。

