數學新情境問題教學的幾點思考

江西省南豐一中 (344500) 肖志強

近年來，教育部相關部門對高考命題提出了不少具體要求，其中強調要“加強情境創設”.并認為“情境是高考評價體系的載體”，情境題能更好地考查學生的創新精神、實踐能力及學生的核心素養，可見情境問題在高考中的重要地位.在數學高考考查方式中，問題情境和情境活動是通過文字與符號的形式進行的“以生考熟”問題轉化的能力.為應對新高考中的情境背景要求，一線教師該采取什么應對的策略呢？

1.準確掌握基本概念，重視概念的生成過程

數學概念是構建數學理論大廈的基石，是導出數學定理和數學法則的邏輯基礎，是數學學科的靈魂和精髓.只有掌握好概念，才能充分認識事物的本質，做出正確的判斷與推理，才能夠更好地解決一些由基本概念衍生出的新情境數學問題.概念教學過程，首先應重視教材中呈現的概念和方法，回顧概念的學習過程，重演定理的推導過程，從而加深對概念的理解并會對重點方法學會應用；其次應以問題為導向進行教學優化,要注意問題設計的有序性,層次性,廣度性,深度性,在有效問題分析探索的基礎上提高對概念的理解,強化“四基四能”,提高數學概念復習教學效果；在掌握和理解了一定的基礎知識后，引導學生領悟深層知識(隱性知識)及其中的指數學思想和方法，使基礎知識的掌握達到一個質的“飛躍”.

案例1 若一系列函數的解析式相同、值域相同，但其定義域不同，則稱這些函數為“同族函數”，那么函數解析式為y=x2，值域為{1,4}的“同族函數”共有________________個．

解析：設函數y=x2的定義域為D，其值域為{1,4}，易知D的所有情形的個數，即是同族函數的個數.D的所有情形為{-1，2}，{-1，-2}，{1，2}，{1，-2}，{-1，1，2}，{-1，1，-2}，{-1，2，-2}，{1，2，-2}，{-1，1，2，-2}，共9個.

上述案例是新定義情境下的函數概念試題，本題給出了函數解析式相同、值域相同但定義域不同的“同族函數”新概念，其實質考查的是學生在新定義情境下對函數三要素的理解.

2.重視閱讀方法引導，培養學生數學閱讀能力

數學閱讀能力是各種數學思維的基礎和前提，其直接影響到學生數學學習過程中問題解決能力的形成和發展.目前學生數學閱讀存在的問題是閱讀能力低，概念模糊，無法理順數據關系，不能順利轉化問題；生活常識匱乏，讀不懂題，在新的情境中學生很難找出關鍵信息，關鍵信息的提煉不到位；教師沒有給予學生閱讀方法指導，忽視學生讀題、審題、分析習慣的養成，等等.為此，教學中應重視閱讀能力的訓練.對概念的學習，要引導學生閱讀，仔細辨析，找出概念的內涵和外延，達到理解要求.公式、定理、法則等教學要突出問題的背景、發生發展過程；解題教學過程中應引導學生認真讀題，明確題意，學會搜集和處理信息的方法.

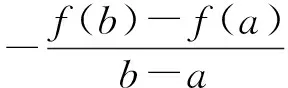
圖1

3.加強問題情景題的訓練，掌握問題解決的化歸思想

“解題就是把要解的題轉化為已經解過的題”，作為問題解決一般的化歸思想，其實質就是“以生考熟”，就是用陌生的問題情境考查熟悉的知識和方法.

圖2

案例3 (2015高考新課標Ⅰ理16)如圖2，在平面四邊形ABCD中，∠A=∠B=∠C=75°，BC=2,則AB的取值范圍是________________.

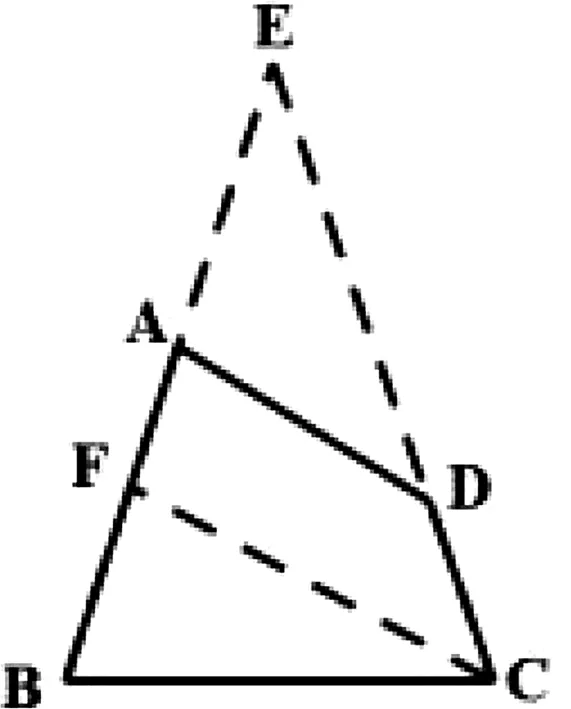
圖3

案例4 (2009高考重慶卷9)已知二面角α-l-β的大小為50°，P為空間中任意一點，則過點P且與平面α和平面β所成的角都是25°的直線的條數為( ).

A．2 B．3 C．4 D．5

解析：設平面α,β的法線分別為m,n，m與n所成的角是50°，過點P的直線與平面所成的角是25°，則與平面的法線所成的角是65°，問題即轉化為：已知兩直線m與n所成的角是50°，則過空間中一點P與m,n所成的角都是65°的直線有幾條？易知選B.

案例5 如圖4，在棱長為2的正方體ABCD-A1B1C1D1中，P是B1C的中點，Q,R分別在BC,BD上，則△PQR周長的最小值為________________．

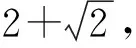
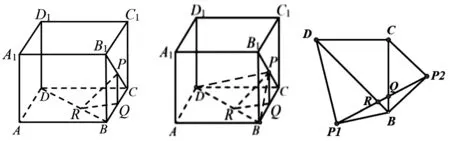
圖4 圖5 圖6

實際上，本題可轉換成問題:如圖5，一只螞蟻從三棱錐P-BCD的頂點P出發,沿表面繞經棱BD和BC回到點P,最短路徑長為________________.

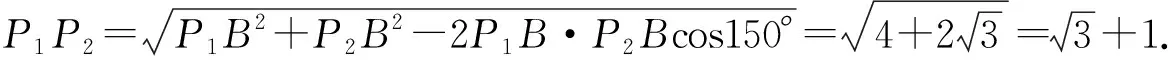
新情境的試題在近年高考中出現的頻率很高，創新更明顯，越加體現出對學生數學應用能力和數學閱讀能力的要求，也體現了對數學學科素養的考查.我們教學中，應更強調牢牢把握數學教學的新課程理念，真正落實從“四基”“四能”到“三會”，再到“核心素養”這一主線，真正達到強化概念基礎、培養數學閱讀能力、掌握化歸思想的目標.