圓外切四邊形涉及旁切圓的一個性質
2021-09-06 03:51:50江蘇省運河高等師范學校221300穎江蘇省蘇州工業園區工業技術學校215000胡甲維
中學數學研究(江西) 2021年8期
關鍵詞:性質
江蘇省運河高等師范學校 (221300) 胡 穎江蘇省蘇州工業園區工業技術學校 (215000) 胡甲維
圓外切四邊形有許多優美的性質,本文給出的是與它內切圓和四個旁切圓相關的一個性質.

圖1
如圖1所示,圓外切四邊形ABCD,與四邊形的一邊及它的兩條相鄰邊的延長線都相切的圓稱為四邊形的一個旁切圓,共有四個旁切圓.旁切圓的三個切點構成的三角形稱為這個旁切圓的切點三角形.四邊形的內切圓與各邊的切點構成的四邊形稱為切點四邊形.設四個旁切圓半徑依次是r1,r2,r3,r4,相對應的四個切點三角形面積依次為S1,S2,S3,S4,內切圓半徑為r,切點四邊形面積為S,則有如下性質:
為了證明上面這個性質,首先證明一個引理.

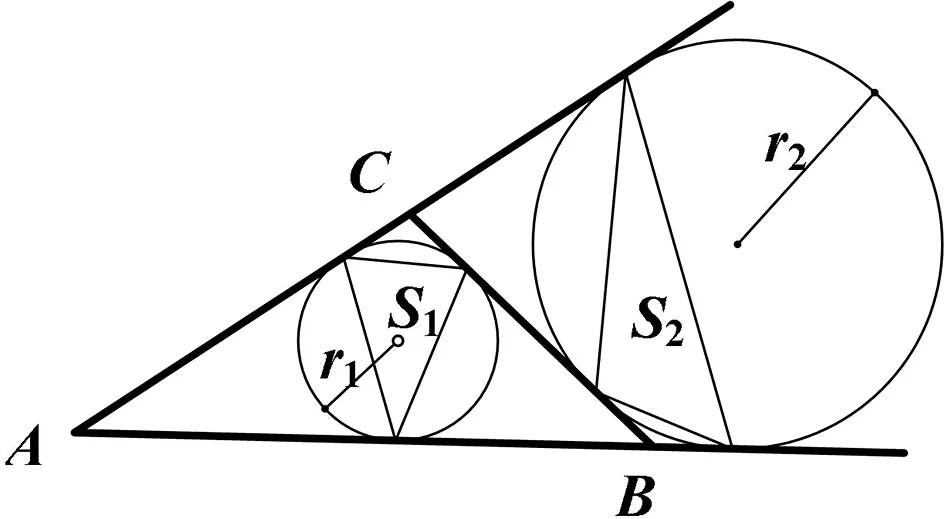
圖2
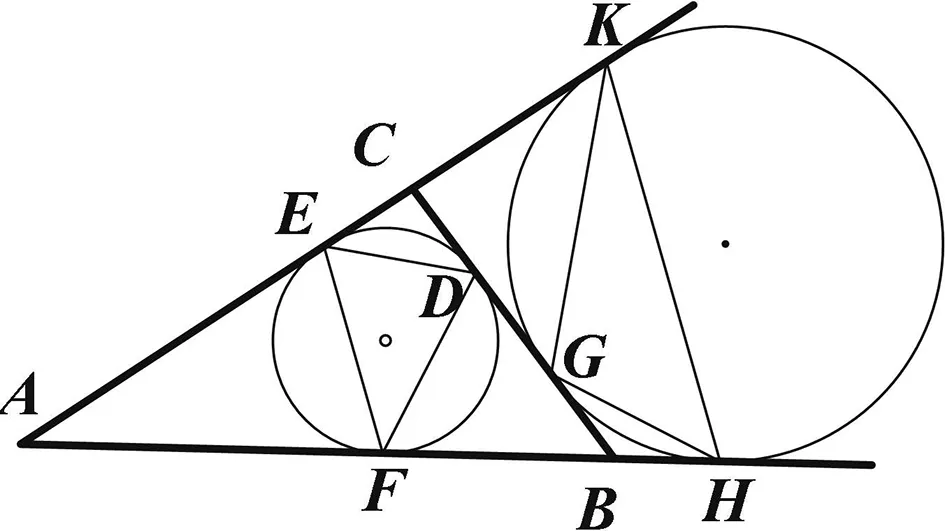
圖3
為了證明上面的引理,先給出并證明下面幾個結論.
結論1 如圖3,兩個切點三角形分別是△DEF和△GHK,則有∠EDF+∠HGK=180°.當然也有sin∠EDF=sin∠HGK.
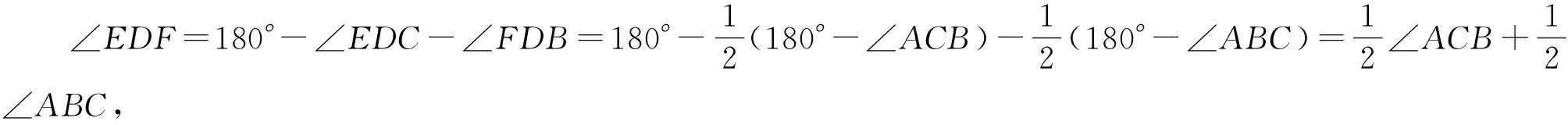
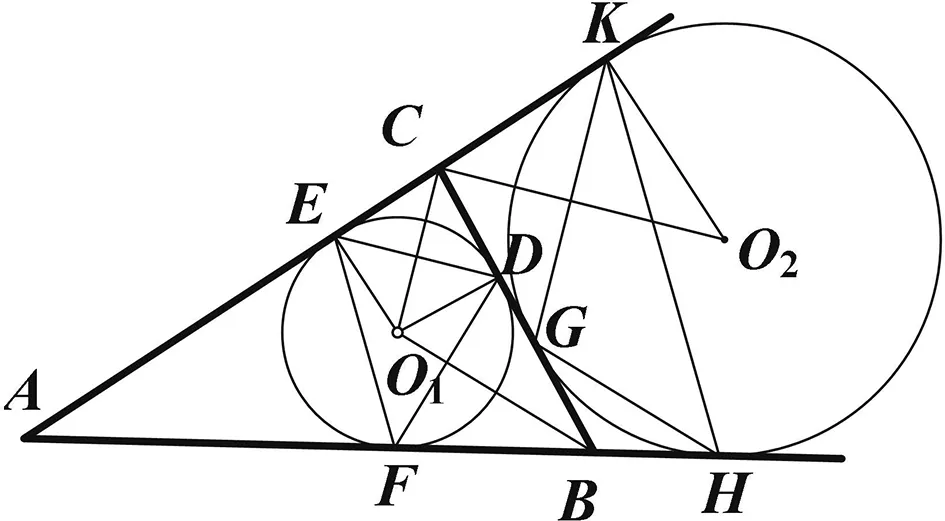
圖4

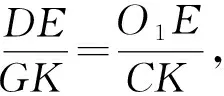
結論3O1B·O1C=O1O2·r1,
O2B·O2C=O1O2·r2.
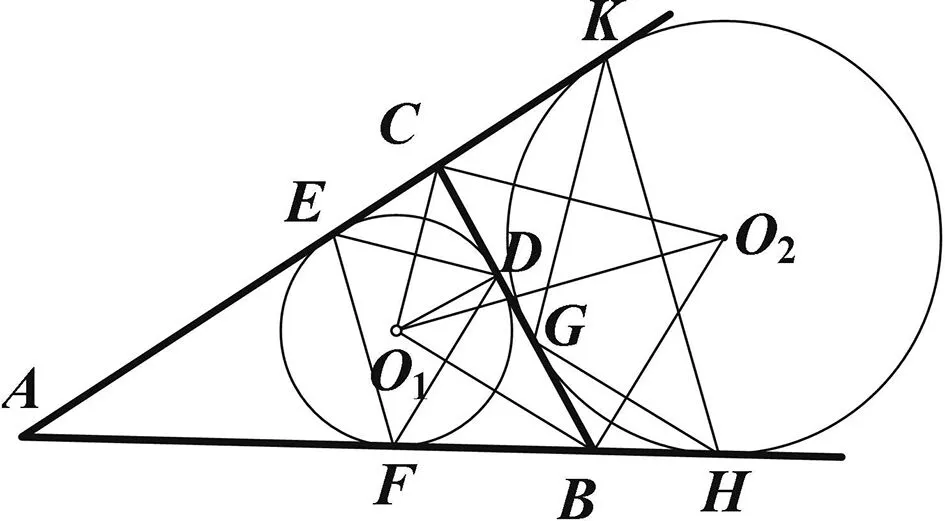
圖5
證明:如圖5,不難看出O1,B,O2,C四點共圓,則∠O1O2C=∠O1BD,由此得O1B·O1C=O1B·O1O2·sin∠O1O2C=O1O2·O1B·sin∠O1BD=O1O2·O1D=O1O2·r1,同理可證O2B·O2C=O1O2·r2.

有了上面的引理,證明本文的性質就容易了.我們分兩種情形來說明.
情形1:圓外切四邊形的兩組對邊分別交于一點.

圖6
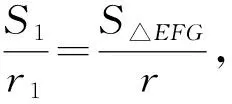
情形2:圓外切四邊形的兩組對邊有一組對邊平行或兩組對邊分別平行.

圖7
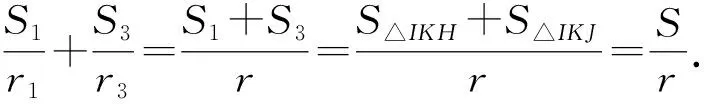
猜你喜歡
中學生數理化·高三版(2023年6期)2023-07-19 11:17:53
數學物理學報(2022年6期)2022-12-15 08:45:02
上海師范大學學報·自然科學版(2022年3期)2022-07-11 03:05:59
數學雜志(2021年6期)2021-11-24 11:12:00
中學生數理化(高中版.高二數學)(2021年5期)2021-07-21 02:14:46
數學年刊A輯(中文版)(2021年1期)2021-06-09 09:31:56
中等數學(2020年6期)2020-09-21 09:32:38
山東農業工程學院學報(2019年11期)2020-01-19 02:49:10
數學物理學報(2019年6期)2020-01-13 06:07:52
中等數學(2019年6期)2019-08-30 03:41:46

