一道直線與橢圓問題的解法與應(yīng)用

江蘇省海門中學(xué) (226100) 蒯 龍

在直線與橢圓的題目中經(jīng)常遇到三角形的面積問題，構(gòu)造三角形的面積有多種途徑，如果將三角形改為四邊形，特別是一般的四邊形，如何求其面積呢？本文通過一道考題的兩種解法來說明如何處理四邊形的面積問題.

一、問題與解

圖1

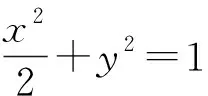
(1)求|AB|(用k表示)；

(2)設(shè)AB與CD交于點(diǎn)Q，AB和CD所成的角為θ，則SACBD=S△AQC+S△CQB+S△BQD+S△DQA

方法一：運(yùn)用角公式得正切、求正弦，構(gòu)造函數(shù)求范圍

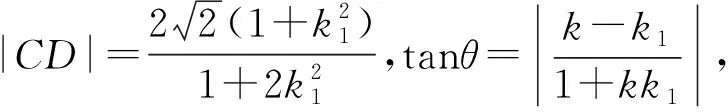
方法二：坐標(biāo)變換將橢圓化為圓，基本不等式求范圍

圖2

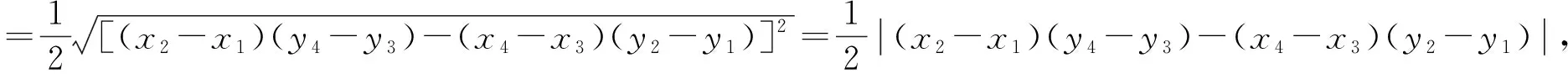
評析：第2問的關(guān)鍵是表示出四邊形的面積，方法一利用到角公式求得兩對角線夾角的正弦值，進(jìn)而利用斜率表示出四邊形的面積,利用函數(shù)單調(diào)性求出取值范圍；方法二，通過變換將橢圓的內(nèi)接四邊形轉(zhuǎn)化為圓中對角線互相垂直的四邊形面積，利用基本不等式求出取值范圍.

二、解法推廣

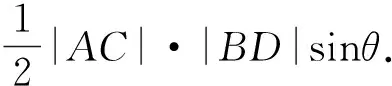
圖3

證明：當(dāng)ABCD是凸四邊形時(shí)，(2)中已證，下證ABCD是凹四邊形時(shí)的情形，如圖3設(shè)AC與BD交于點(diǎn)E，則SABCD=S△AEB+S△BEC-S△AED-S△CED

上述命題說明任意四邊形的面積就是以對角線平移后構(gòu)成的三角形的面積，由解法二可得到三角形面積的坐標(biāo)公式.

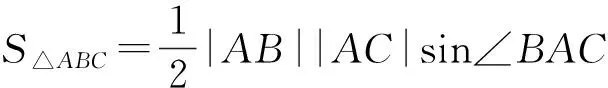
根據(jù)上述命題只需知道三角形3個(gè)頂點(diǎn)的坐標(biāo)，便可以求出三角形的面積，解法二中依據(jù)上述坐標(biāo)公式可以得到變換前后三角形面積之間的關(guān)系.

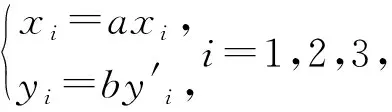
三、綜合應(yīng)用

例1 (2021廣州市一模)已知點(diǎn)A(1,0)，點(diǎn)B是圓O1:(x+1)2+y2=16上的動點(diǎn)，線段AB的垂直平分線與BO1相交于點(diǎn)C，點(diǎn)C的軌跡為曲線E.

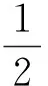
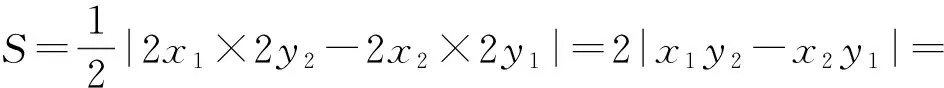
結(jié)語：涉及四邊形的面積問題，關(guān)鍵在于如何表示面積，命題1與命題2用坐標(biāo)表示四邊形的面積，避免了討論四邊形的形狀，運(yùn)用了數(shù)形結(jié)合的思想，將幾何問題轉(zhuǎn)化為代數(shù)方法處理，體現(xiàn)了解析幾何的思想.命題3中的變換，實(shí)現(xiàn)了將橢圓中的問題轉(zhuǎn)化為圓中的問題，使得問題的幾何特征更為明顯，運(yùn)用了轉(zhuǎn)化與化歸的數(shù)學(xué)思想.