函數有唯一零點問題的多視角分析

陜西省西安市第八十九中學 (710003) 彭文靜

函數零點是連接函數與方程兩大問題的橋梁，是高考復習的熱點問題，該知識往往滲透于綜合題中，對學生邏輯思維能力要求高.函數y=f(x)為零的自變量x的值即為函數的零點，即方程f(x)=0的根，也即y=f(x)圖像與x軸交點的橫坐標.其等價關系如圖：

函數零點的多角度分析過程體現了轉化與化歸、數形結合、分類討論等數學思想方法，筆者以一道函數零點問題為例從四個方面進行剖析.

1、題目呈現

題目當x∈(1,+∞)，函數f(x)=xlnx+(1-k)x+k有唯一零點，求距離k最近的整數.

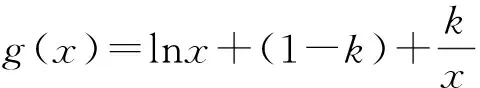
2、具體解法

視角1：直接切入找零點，分類討論需謹慎

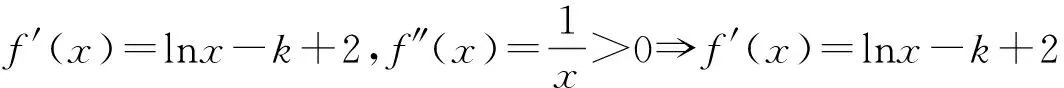
點評：該解法中依據k-2與0的大小關系，將參數k分兩種情況討論.其中在情形②中，f′(x)=lnx-k+2=0在(1,+∞)有且只有一個解，該方程為超越方程，則要“虛設”零點，設而不求，然后由函數f(x0)單調性，借助零點存在性定理，憑號定論零點存在區間，這是解決該問題的核心思想，最后就是利用二分法進一步縮小根的存在區間，以此確定k的整數值.

視角2：函數角度求交點，數形結合顯直觀

圖1

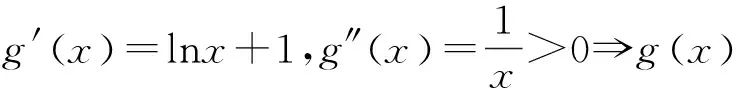
點評：該方法清晰明快，避免了參數的分類討論，但找準兩個基本函數是關鍵，一般以能畫出兩個函數圖像為原則，如本題中的下凸函數圖像和直線.

視角3：完全分參探性質，研究最值是關鍵

圖2

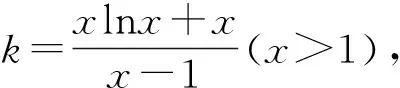
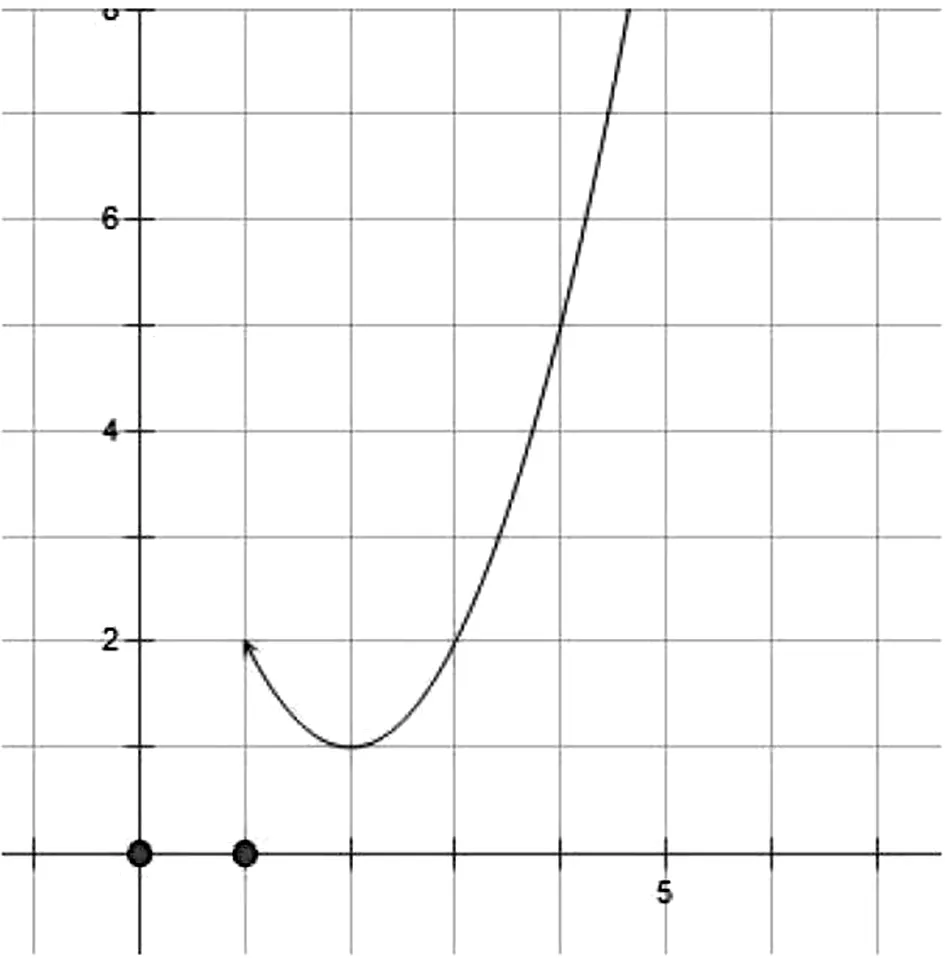
圖3

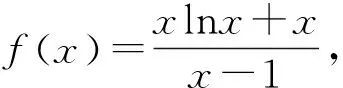
視角4：“降維”變形巧構造，等價轉化是本質

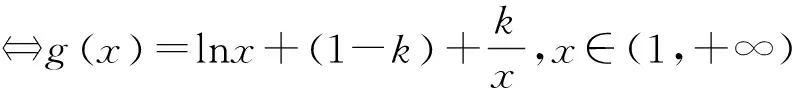
函數零點是連接函數與方程兩大思想問題的橋梁，而已知零點個數唯一求參數的取值范圍是函數零點問題的常見題型之一，其本質是函數單調性、極值、最值的應用，涉及到的具體思想方法有數形結合、分類討論及轉化與劃歸思想.本題從四個不同視角分析零點唯一性問題，解題方法迥異.其中，解法1直接切入普遍常規，學生易于著手，但解答完整還需較強的導數功底及邏輯思維能力，其中找準分類討論的切入點和解決超越方程的“隱零點”是兩個關鍵點；解法4進行等價變形后直接分析新函數的性質，本質與解法1相同，但比解法1簡單原因是沒有超越方程的出現，便于解決問題.解法2分離參數操作簡單，備受學生青睞，直接求分參后新函數的值域或最值即可，但缺點在于新函數的最值可能無法求得，需要借助于“洛必達法則”，亦或是新函數解析式過于復雜，無法進行下去等等；解法3數形結合比較直觀，唯一零點找臨界可用切線法，但需要有較強的圖形分析能力.

由函數零點的唯一性進而可以拓展到求函數零點個數問題，其基本解決途徑如上，在做題過程中，對該四種解法的綜合評估、確定最優解法的過程其實也是提高學生分析問題、解決問題、落實數學核心素養的途徑.只要用心思考、靈活轉換，抓住導數性質這一有力工具，則函數零點個數問題將不再是難題.