基于BAS-PID算法的介電彈性體執行器控制研究

徐 健，惠 楠，蘇澤斌

(西安工程大學 電子信息學院，陜西 西安 710048)

0 引 言

軟體機器人在勘探、救援、醫療等領域有廣闊的應用前景。DEA作為軟體機器人，具有能量密度高[1]、變形大[2]等特點，并且可以完成移動、抓取等任務[3]。但DEA具有黏彈性的特點限制了在機器人領域的運動精度，為了實現對DEA的有效控制，可采用流變模型對DEA進行建模，從而模擬DEA的黏彈性效應[4]。對于DEA的控制分為前饋控制和反饋控制[5]。反饋控制相對于前饋控制具有更理想的控制精度，采用PID控制DEA具有較好的跟蹤性能[6]。PID控制的難點在于其參數整定問題，不同參數的整定方法會對PID的性能產生巨大差異，常規的PID參數整定方法相對復雜，很難實現最優整定參數[7-8]。

針對傳統PID控制的缺點，采用仿生智能算法優化PID參數是一種有效的方法。BAS算法是近年來提出的一種仿生優化算法，在不需要函數的具體形式情況下，就可以實現高效尋優[9]。BAS算法的生物原理是一種通過模擬天牛覓食時根據觸角來接收的食物氣味強弱，確定搜索方向，最終找到全局最優參數的一種新型智能優化算法[10]。該算法有2個優點：第一，不需要知道函數具體形式和梯度信息；第二，能夠降低運算量，縮短尋優時間[11-12]。

針對介電彈性體構成的執行器在驅動過程中存在難以精準控制的缺點，提出采用BAS算法和PID結合的控制方法來實現對DEA的精確控制。為了給DEA后續的實際應用提供理論依據，建立了DEA的動力學模型，利用Matlab/SIMULINK對所建立的模型和控制算法進行了仿真研究，控制系統采用BAS算法，對PID進行參數優化，實現對DEA的有效控制。

1 DEA動力學模型

介電彈性體在外加電壓作用下會發生形變，當給柔性電極加載電壓，在電場的作用下介電彈性體表面會積累正負電荷，導致介電彈性體厚度變薄且平面方向上擴張變形；當柔性電極電壓卸載，介電彈性體會恢復至原狀，則介電彈性體實現從電能到機械能的轉化[13]。DEA是由介電彈性體材料和柔性骨架組成的軟體機器人。DEA在電能和機械能轉化過程之中存在黏彈性效應[14]。因此，可采用流變模型中的彈簧阻尼器對DEA的黏彈性效應導致的非線性運動進行建模[15]。

DEA模型的動力學方程可表示為

(1)

式中：i=1,2,3,4；xi為彈簧變形；此模型中表示黏彈性的彈簧阻尼動力學由2個單元組成，彈簧k為一個單元，彈簧ki和阻尼器ci組成另一個單元；m為DEA的質量，此處取9 g；Φ為DEA的驅動電壓；Ω(x)為DEA長度變化的線性函數；ζ為DEA運動過程中的阻力;當x′>0，sgn(x′)=1；當x′=0，sgn(x′)=0；當x′<0，sgn(x′)=-1，為了保證系統的穩定性，可以采用PID使DEA的誤差收斂。

在DEA模型中，將式(1)中Φ2作為PID的輸出，有

(2)

式中：i=1,2,3,4；x為DEA的輸出；ζsgn(x′)/m為由摩擦力導致的擾動，并且有界可收斂。

2 BAS-PID控制算法

PID是一種基于過去、現在和未來信息估計的算法[16]。PID參數，即比例參數Kp、積分參數Ki和微分參數Kd[17]。比例參數Kp反映系統偏差，通過調節能夠提高系統靈敏度及系統穩定性；積分參數Ki作用是消除系統穩態誤差，改善系統無差度；微分參數Kd反映偏差信號變化規律，依據這些規律進行超前控制調節，改善系統能動性。BAS算法和傳統PID算法相結合，使得控制系統可以利用BAS算法的參數優化能力來調整PID的參數。基于BAS算法的PID控制框架如圖1所示。

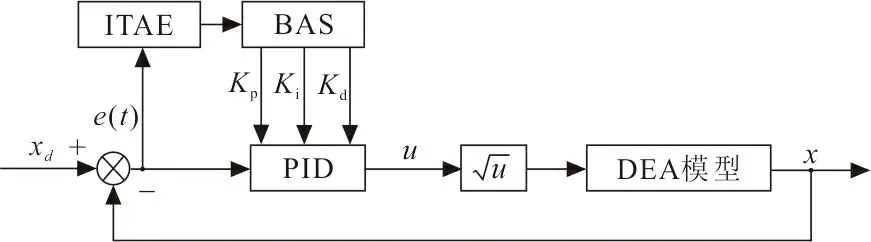
圖 1 DEA控制系統Fig.1 DEA control system

圖1中，ITAE為時間乘以絕對誤差的積分，xd為期望位移,x為輸出位移,u為PID的輸出量,DEA的位移受到電壓平方的影響，DEA的輸入為電壓信號Φ，而PID的輸出量u為電壓平方Φ2，所以將PID控制量的平方根作為DEA的輸入。BAS算法可以通過基于誤差的ITAE函數對PID參數進行優化，在迭代過程中，減小DEA產生的誤差，從而提高DEA的驅動精度。

BAS算法是一種元啟發式智能優化算法[18],天牛每次的運動軌跡就是一個優化解決方案。BAS算法的適應度函數選用ITAE作為指標[19-20]，可表示為

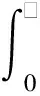
(3)

式中：e(t)為系統產生的誤差。PID參數整定可以轉化為BAS算法的三維參數優化問題。在BAS算法迭代過程中，利用天牛的位置來更新PID參數。當PID控制系統的性能滿足要求或搜索過程達到最大迭代次數時，以天牛的最佳位置作為最終的PID參數。BAS-PID控制器的參數整定步驟如下。

1) 初始化天牛位置和天牛須的朝向信息，天牛朝向信息可表示為

(4)

式中：D賦值為3，為優化參數的維數；rand()為[0,1]之間的一個隨機數。

2) 天牛三維位置參數分別賦值給Kp、Ki和Kd，運行PID控制系統進行仿真。

3) 將PID控制系統產生的誤差代入適應度函數G中計算當前適應度值。

4) 每次迭代產生的適應度值和對應的PID參數按照適應度從大到小進行存儲更新。

5) 判斷是否迭代到最大迭代次數T=80或適應度值G≤0.01，若未達到，則天牛觸須三維參數分別賦值給Kp、Ki和Kd，運行控制系統進行仿真。計算觸須適應度值，并且觸須長度lt和步長δt以及左右觸角位置pl、pr采用式(5)進行更新，并且天牛向適應度小的方向進行移動。

(5)

式中：lt為天牛在t時刻觸須的長度參數；δt為天牛t時刻的步長參數；dt為天牛在t時刻觸角之間的距離參數；pt為天牛在t時刻的位置參數；pr為天牛右觸須的位置參數；pl為天牛左觸須的位置參數。

6) 天牛位置參數采用式(6)更新，并且返回第2)步進行循環迭代。

pt+1=pt+?tbsgn(G(pl)-G(pr))

(6)

式中：sgn函數用來返回步長參數的正負，當G(pl)大于G(pr)時，天牛向左移動，當G(pl)小于G(pr)時，天牛向右移動，當G(pl)等于G(pr)時，天牛保持原位置不動。

7) 當迭代次數T=80或適應度值G≤0.01，迭代結束。從存儲的PID參數和適應度值中輸出最優PID參數和對應的適應度值。BAS-PID工作流程如圖2所示。

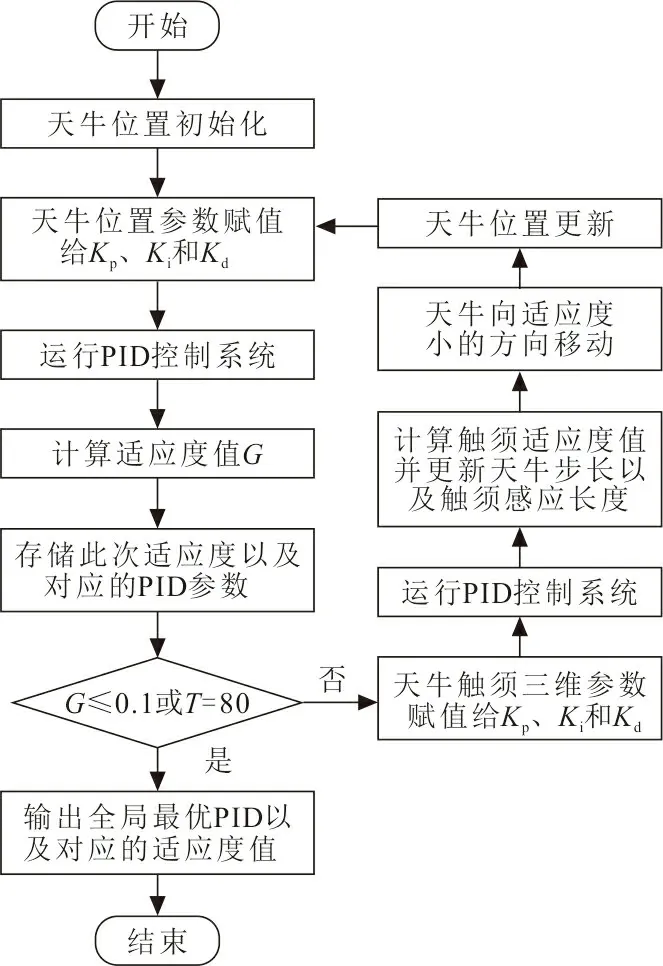
圖 2 BAS-PID工作流程Fig.2 BAS-PID workflow

圖2中，BAS-PID在迭代過程中采用多只天牛搜索、變步長和變觸須長度增強全局搜索能力，同時避免陷入局部最優，由于天牛初始位置隨機，所以通過設定天牛的位置邊界的方式，提高BAS算法搜索最優PID參數的準確性。

3 仿 真

為了驗證本文提出的BAS-PID控制方案的有效性，在Matlab/SIMULINK中搭建PID控制系統和DEA模型，并將BAS算法在M文件中實現。在BAS運行中調用PID的數據，對PID參數進行迭代優化。BAS算法參數：種群數量為10，初始步長δ0=5，最大迭代次數T=80，適應度函數最小精度G=0.01。在仿真實驗中，BAS-PID在迭代過程中的適應度曲線如圖3所示，BAS-PID、BP-PID和PID對不同參考信號的跟蹤效果如圖4所示。

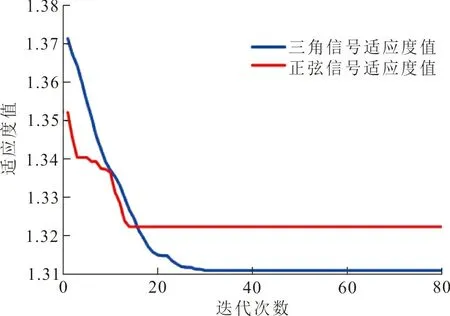
圖 3 BAS-PID適應度值的迭代曲線Fig.3 Iterative curve of BAS-PID fitness value

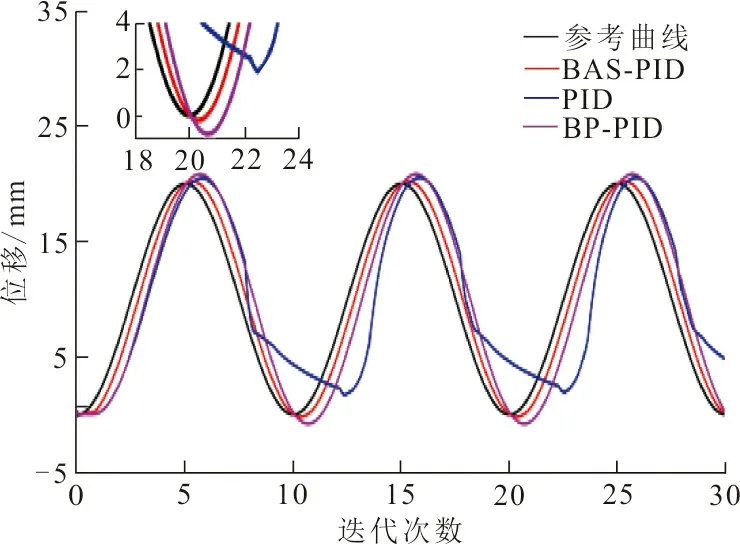
(a) 不同控制算法正弦信號跟蹤曲線

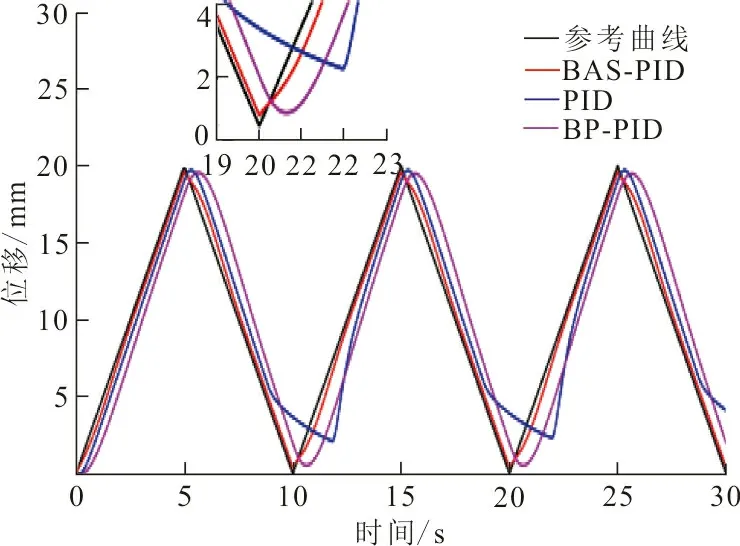
(b) 不同控制算法三角信號跟蹤曲線圖 4 不同控制算法跟蹤曲線對比Fig.4 Curve tracking of different control algorithms

從圖3可看出，當參考信號為正弦信號和三角信號情況下，BAS算法分別在的第14次和第30次迭代時，搜索到最優PID參數，最小的適應度值分別為1.32和1.31，由此可見，BAS-PID在收斂速度上取得較好結果，能夠用較少的迭代次數達到最優值。從圖4可看出，PID算法和BP-PID算法在不同波形的參考信號拐點處都存在較大誤差，這主要是由于黏彈性效應導致控制器難以及時響應，所以PID算法和BP-PID算法在拐點處都存在明顯滯后于參考曲線。BAS-PID算法在不同波形的參考曲線拐點處、上升和下降部分均可以進行有效跟蹤，在控制過程中減少了DEA黏彈性影響，提高了DEA的控制精度。仿真結果說明：BAS-PID算法的調節能力相較于PID算法和BP-PID算法能夠更準確跟蹤DEA的參考信號，具有良好的控制性能。

為了量化3種控制算法的優劣，選取最大跟蹤誤差emax和均方根誤差erms進行對比，最大跟蹤誤差emax和均方根誤差erms采用式(7)進行計算，具體精度參數如表1所示。

(7)

式中：x為輸出位移；xd為期望位移；N為采樣的次數。

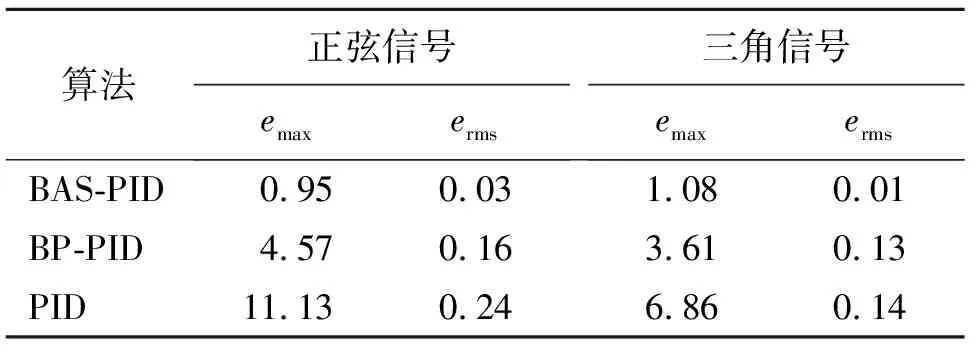
表1 不同控制算法精度參數

從表1可看出，在正弦輸入信號下，BAS-PID比常規的PID最大跟蹤誤差降低10.08 mm，均方根誤差降低0.21 mm，在三角輸入信號下，BAS-PID比常規的PID最大跟蹤誤差降低5.78 mm，均方根誤差降低0.13 mm。BP-PID的控制精度優于常規PID但仍有較大誤差。文獻[15]所提出的生物啟發控制方法對于正弦信號的最大跟蹤誤差為0.97 mm，均方根誤差為0.47 mm。BAS-PID的最大跟蹤誤差為0.95 mm，比生物啟發控制方法的最大跟蹤誤差略有降低，均方根誤差從0.47 mm降低至0.03 mm。

4 結 語

本文提出并使用BAS-PID算法完成了對介電彈性體執行器驅動控制方法的研究。首先,建立了介電彈性體執行器的模型并對其驅動過程中的黏彈性效應進行模擬驗證；其次，詳細介紹了BAS-PID算法，將BAS算法中天牛的三維信息引入PID參數中，在迭代優化過程中，使得衡量系統穩定性的ITAE適應度函數減小，解決DEA存在的黏彈性問題；最后,通過仿真對比實驗驗證了BAS-PID、BP-PID、PID控制算法的控制效果，其中BAS-PID算法產生的誤差更小，說明本文的控制算法可以實現介電彈性體執行器的精確控制。