Abundant Exact Solutions for Differential-Difference Equations Arising in Toda Mechanics

WANG Yan (王 燕)， AN Jianye (安建業)， LIU Jiangen (劉建根)

1 School of Sciences, Tianjin University of Commerce, Tianjin 300134, China

2 School of Mathematics, China University of Mining and Technology, Xuzhou 221116, China

Abstract: For a discontinuous Toda medium, a differential-difference equation(DDE) can be established. A modification of the exp-function method is applied to construct some soliton-like and period-like solutions for nonlinear DDEs with variable coefficients. The solution process is simple and straightforward and some new solutions are obtained with full physical understanding.

Key words: rational expansion method; discrete hybrid equation; soliton-like solution; period-like solution; exp-function method; Toda mechanics

Introduction

It is the known fact that nonlinear evolution equations are usually used to describe complex phenomena, including physics, mechanics, biology, and so on. The investigation of exact solutions of nonlinear evolution equations plays an essential role in the study of these phenomena. In the past several years, many feasible methods were proposed for finding exact solutions of these evolution equations by a lot of workers, such as the Hirota bilinear method[1], the tanh method[2-4], the exp-function method[5-7], the rational expansion method[8-9], the(G′/G)-expansion method[10-11], the Lie symmetry method[12], the Jacobin elliptic function method[13-14], and other ways.

Here, differential-difference equations (DDEs) play a major role in modeling of many physical phenomena arising in Toda mechanics, for example, particle vibrations in lattices (Toda medium), currents of electrical networks and pulses in biology. Unlike the difference equations which are fully discrete, DDEs are semi-discrete with some (or all) of their special variables discrete while time part is kept to be continuous. Since the work of Fermietal.[15]in 1950s, many researchers made lots of works on it. Zhu[6]extended the exp-function method to nonlinear differential-difference equations (NDDEs) to obtain physically important solutions. Baldwin[3]applied the tanh-method and its extended form to DDEs and obtained a series of exact solutions. Levi and Yamilov[12]analyzed the condition for existence of higher symmetries for a class of DDEs ,etc.

In this paper, we apply the rational expansion method, a modified exp-function method[16-20], to directly construct some new analytical solutions for the discrete hybrid equation. As a result, the soliton-like and period-like solutions have been obtained.

1 Description of Rational Expansion Method

The exp-function method was proposed by Heetal.[16-20], and it is mainly applicable to solitary waves. In this present section, we present the main steps of the method for solving nonlinear DDEs by a modification of the exp-function method, which is also called the rational expansion method[8-9].

First, for a given nonlinear DDEs

(1)

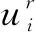
Step1We suppose the solutions in the following form

(2)

whereh(x) is an arbitrary function with respect tox, andaijis an arbitrary constant. The new functionsφnandψnshall be selected as a series of functions which consists of an autonomous system.

Repeatedly applying the chain rule

(3)

the polynomial Eq. (1) can be turned into the following form

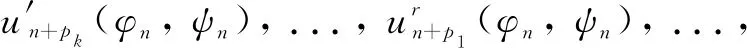
(4)

Remark1It is noted that for anyl(l=1, 2,...,k)，un+plin Eq. (4) are required to be functions ofφnandψn.

Family1Ifφn=ψn=tanh, then, according to the identity

(5)

we have

(6)

where

γs=ps·d=ps1d1+ps2d2+...+psQdQ,

(7)

andpsjis thejth component of shift vectorps.

Family2Assumeφn=1 andψn=tanh, we have the similar result.

Family3Assumeφn=ψn=tan, then, according to the identity

(8)

we have

(9)

whereγsis determined as in Eq. (7).

Family4Assumeφn=1 andψn=tan, we have similar results.

Remark2There are many choices forφnandψnto construct an autonomous system, such asφn=sinh,ψn=cosh,φn=tanh,ψn=sech,φn=sinh, andψn=cosh.

Step2Determine the degree of the polynomial solutions. In order to obtain the solutions of the form Eq. (2), we need to ensure the value of the leading termMi.As the framework in the continuous case, we can give the leading-term analysis[3].

Step3Derive the differential equation system foraijandh(x).Substitute

(10)

into Eq. (4) with alongγsas in Eq. (7).

Step4According to Families 1-4 of the algebra system, collecting the coefficients ofφnandψn, and we set them to be zero, this action yields a set of algebraic equations. Solving this algebraic equations system and substituting these value into Eq. (2), we can obtain the exact solutions of Eq. (1) instantly.

2 Applications

In this section, we use the rational expansion method to find some new exact solutions for the discrete hybrid equation arising in Toda mechanics. The discrete hybrid equation can be written as[21]

(11)

whereαandβare arbitrary parameters. For Eq. (11), by using the leading term analysis we obtain the degree of polynomial solutions is 1.

Corresponding to Family 1, we have

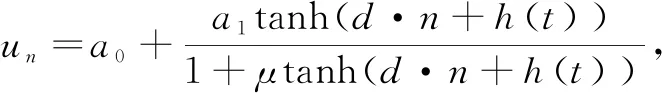
(12)

whereh(t) is an arbitrary function with respect tot.a0anda1are arbitrary constants.

Substituting Eq. (12) into Eq. (11) and collecting the same power terms of tanh(d·n+h(t)) as well as solving the over-determined system by Maple, we could obtain the values fora0,h(t) anda1.

Case1

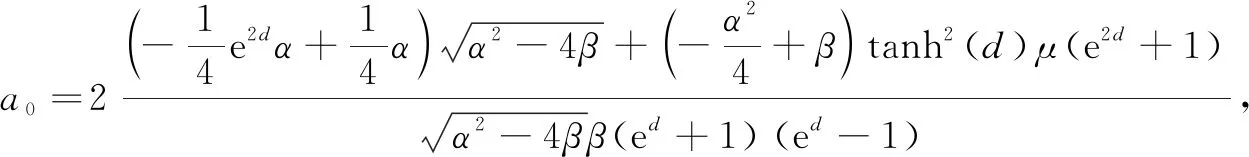
(13)

whereC1is an integral constant.

Case2

(14)

whereC2is an integral constant.

Then, we can obtain the soliton-like solutions to Eq. (11).

(15)

wherea0,a1andh(t) are the values of Case 1 and Case 2, as illustrated in Fig. 1.

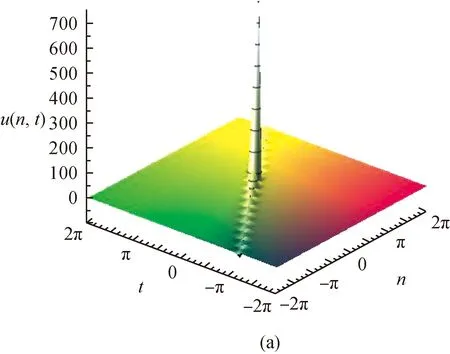
Fig. 1 Soliton-like solutions of Eq. (15) with d=1, α=2, β=0.5, μ=2, C2=0 in the sense of Case 2:(a)3D-pot;(b) 2D-pot

Corresponding to Family 2, we have

(16)

whereh(t) is an arbitrary function with respect tot,a0anda1are arbitrary constants.

Proceeding as the previous steps, and substituting Eq. (17) into Eq. (11), we obtain the values fora0,h(t) anda1.

Case3

(17)

whereC1is an integral constant.

Case4

(18)

whereC2is an integral constant.

Then, we can obtain the soliton-like solutions to Eq. (11).

(19)

wherea0,a1andh(t) are the values of Case 3 and Case 4.

Corresponding to Family 3, we have

(20)

whereh(t) is an arbitrary function with respect tot,a0anda1are arbitrary constants.

Substituting Eq. (20) into Eq. (11), we obtain the values fora0,h(t) anda1.

Case5

(21)

whereC1is an integral constant.

Case6

(22)

whereC2is an integral constant.

Then, we can obtain the period-like solutions to Eq. (11).

(23)

wherea0,a1andh(t) are the values of Case 5 and Case 6, as illustrated in Fig. 2.

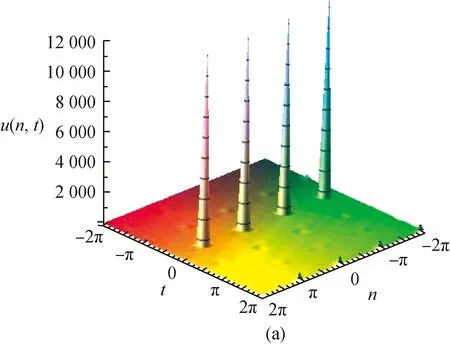
Fig. 2 Period-like solutions to Eq. (23) with d=1, α=2, β=0.5, μ=2, C2=0 in the sense of Case 6: (a) 3D-pot; (b) 2D-pot

Corresponding to Family 4, we have

(24)

whereh(t) is an arbitrary function with respect tot,a0anda1are arbitrary constants.

Substituting Eq. (24) into Eq. (11), we obtain the values fora0,h(t) anda1.

Case7

(25)

whereC1is an integral constant.

Case8

(26)

whereC2is an integral constant.

Then, we can obtain the period-like solutions to Eq. (11).

(27)

wherea0,a1andh(t) are the values of Case 7 and Case 8.

Remark3Here, we pointed out that these solutions are new solutions, which are more interesting than those obtained before.

3 Conclusions

In this paper, we employed the rational expansion method to obtain some new soliton-like and period-like solutions for the discrete hybrid equation arising in Toda mechanics. This approach is easily carried out for calculating, and it is a direct and efficient as well as powerful method, which can be used to various discrete equations possessing strong physical backgrounds.