基于概率統計的水電機組狀態監測參數波動預警策略
周寧剛,徐劍峰,江書樵,陳澤陽
(1.浙江華電烏溪江水力發電有限公司,浙江省衢州市 324000;2.北京華科同安監控技術有限公司,北京市 100043)
0 引言
自20世紀90年代起,水電機組狀態監測系統陸續在各大水電廠投運,至今已得到廣泛應用,實時監測水電機組的振動、壓力脈動、噪聲等特征參數,當出現異常時及時做出預警,保障水電機組的安全運行[1]。近年來,行業內對水電機組狀態監測數據開展了多種數據挖掘研究,探索更完善、更科學的預警模式。參考文獻[2]對某機組在一定時段的不同監測值進行了概率統計,證明了不同監測值的概率分布與正態分布較為接近。參考文獻[3]對機組軸瓦溫度進行了統計分析,并進行了嚴格的分布檢驗,證明了軸瓦溫度數據的樣本均值序列服從正態分布。參考文獻[4]和參考文獻[5]對比了不同的概率統計方法對狀態監測數據統計特性的影響。參考文獻[6]對基于不同統計原理的故障診斷方法做了梳理和對比。參考文獻[7]設計了基于機器學習的水電機組監測參數預警模式。但時至今日,狀態監測系統的預警方式仍多以單一的限值作為預警依據,即當實時監測值超過預設的閾值時做出預警。對此,本文根據正態分布理論,對狀態監測參數的波動特性開展統計分析,探尋機組潛在的狀態變化,進而對其波動中出現的異常進行預警,以期改善單一閾值的越限預警方式,提高水電機組的安全運行系數。
1 波動預警原理
水電機組屬于慢速旋轉機械,運行特性經常處于緩慢變化的狀態,在系統工作正常的前提下,監測參數較少出現突然跳變的情況。若機組由于某種故障或潛在隱患的不斷惡化,運行狀態已在發生緩慢的劣化,但監測參數尚未超過預設的閾值,此時單一閾值的預警方式難以察覺。此外,水電機組監測參數的單一預警限值大多來自于相關國內、國際標準中對應的規定,即便設置了多個單一閾值進行分級報警,仍為單一的數值越限預警模式,不能監測到特征參數正在發生的緩慢變化。這就導致故障已經發生或設備已惡化到一定程度才被發現,給機組的安全運行帶來隱患,增加未預期的檢修成本。
根據概率統計學中的中心極限定理,對于容量足夠大的數據樣本,其采樣均值服從正態分布[8],可利用正態分布的理論對其進行分析。
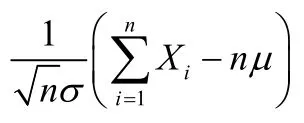
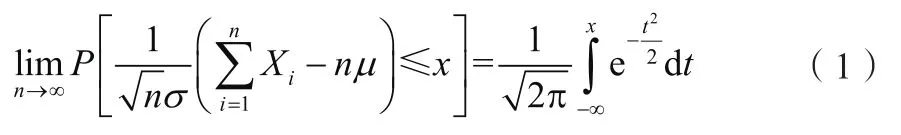
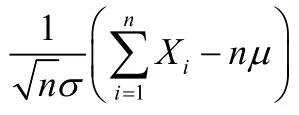
中心極限定理表明,只要采樣樣本容量n足夠大,多次采樣的樣本均值序列服從正態分布。對水電機組而言,特征參數的每一個實時監測值由系統根據實時采集波形獨立計算得出,不同的監測值之間相互獨立,且由于其監測同一特征參數,不同的監測值服從同一概率分布。不管該概率分布為一明確的還是未知的數學分布,其均值序列均應服從正態分布。但值得注意的是,中心極限定理表述的是監測值的樣本均值序列服從正態分布,而非不同監測值構成的序列本身服從正態分布。因此,不可盲目地對任一監測參數的數據序列進行概率統計分析,即便其近似服從正態分布,也屬偶然現象,且缺乏中心極限定理的理論支持,必須經過嚴格的正態分布檢驗,才可利用正態分布的理論進行分析。
根據中心極限定理,若某一監測參數的采樣樣本均值序列服從正態分布,即可對該參數n次采樣的均值進行監測和預警。由于監測參數的均值反映的是該參數在穩態工況下的緩慢波動,本文定義該預警模式為波動預警。具體而言,根據正態分布的理論,監測參數實時值位于3σ區間內的概率為99.74%,即99.74%的概率下,監測值會在3σ區間內波動,如果數據波動超出了這一區間,監測參數出現異常的概率為99.74%。因此,可采用3σ準則設定參數的波動閾值:

式中:μ——樣本均值;
σ——樣本標準差。
2 波動預警的實現
選取國內某水電機組滿負荷穩定運行10h積累的監測數據進行概率統計分析,包括上導擺度+X、上機架水平振動+X、蝸殼進口壓力脈動、發電機層噪聲4個監測參數。狀態監測系統每3s保存一組實時數據,以上每個監測參數分別包括12000個數據點,作為統計分析的總體P。
2.1 概率特性統計
4個監測參數的時域分布如圖1所示。從圖中可以看出,由于機組在滿負荷穩定運行,各監測值均保持穩定,偶有數值出現突然增大或減小的現象,但未超過系統預設的單一報警閾值,系統不會作出預警。
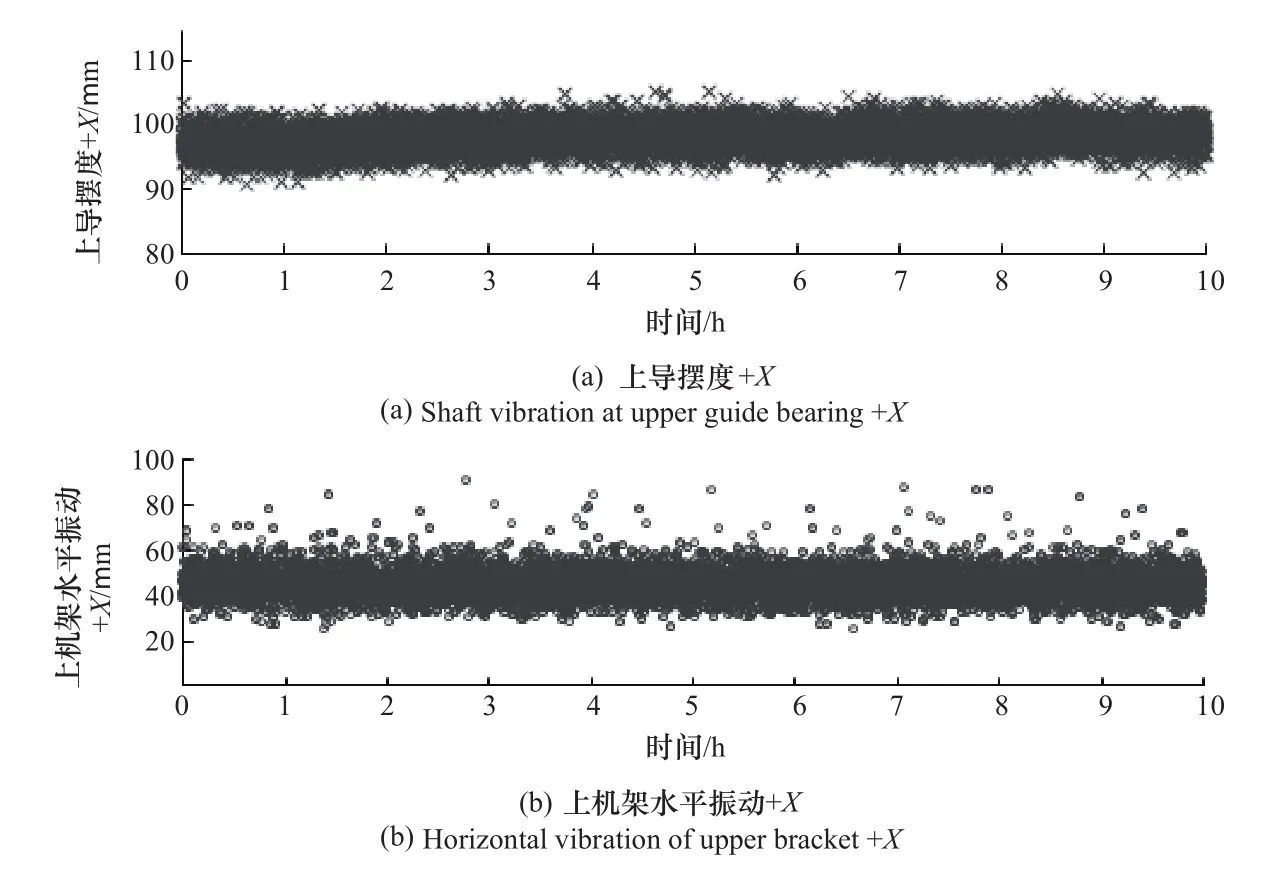
圖1 監測參數時域分布圖(一)Figure 1 Time-domain diagrams of monitoring parameters(No.1)
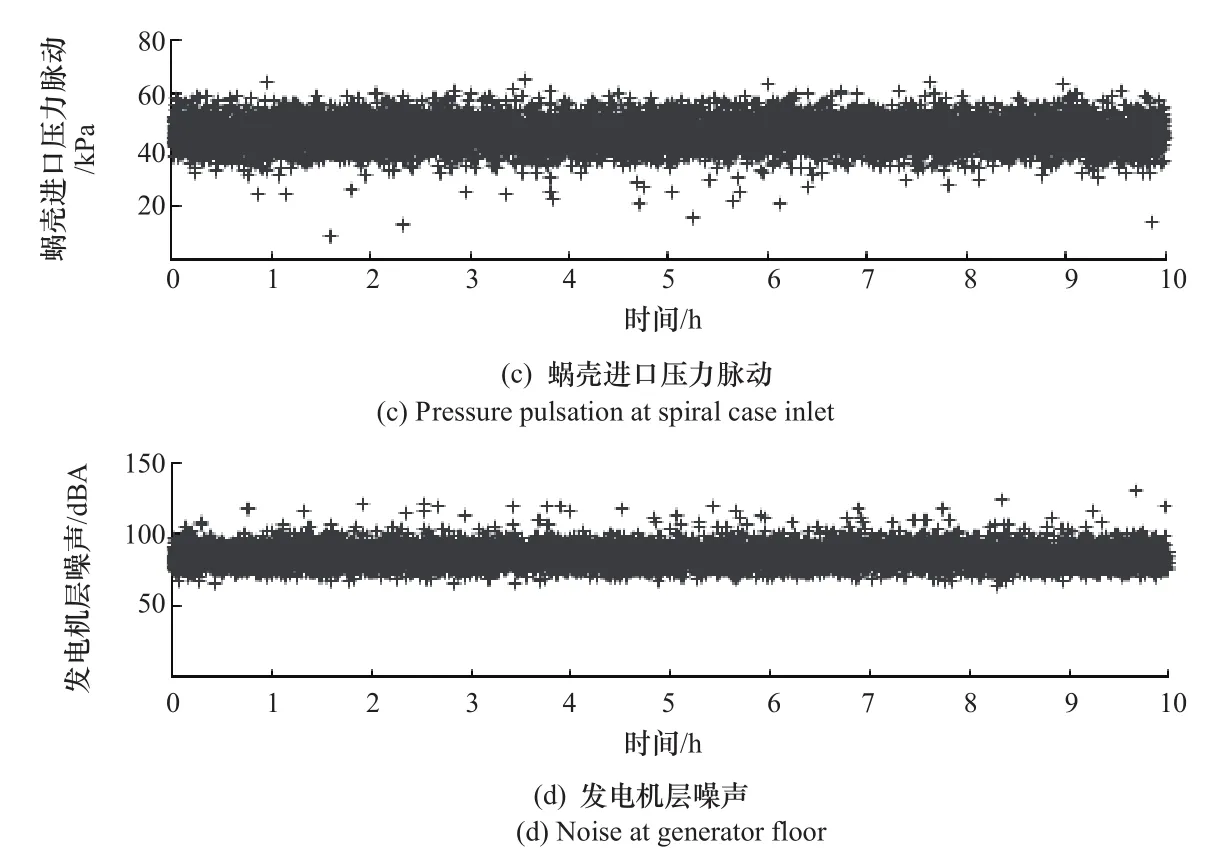
圖1 監測參數時域分布圖(二)Figure 1 Time-domain diagrams of monitoring parameters(No.2)
2.2 數據分布驗證
對每個監測參數,按照以下步驟進行數據分布檢驗:
(1)在總體P中進行n次采樣,得到n個樣本值x1,x2,…,xn,計算樣本均值;
(3)利用MATLAB中的Jbtest函數對樣本均值序列進行正態分布檢驗。
4個監測參數的概率密度分布如圖2所示。累積概率分布如圖3所示。從圖2和圖3可以看出,監測數據的概率分布近似服從正態分布。正態分布檢驗結果如表1所示。
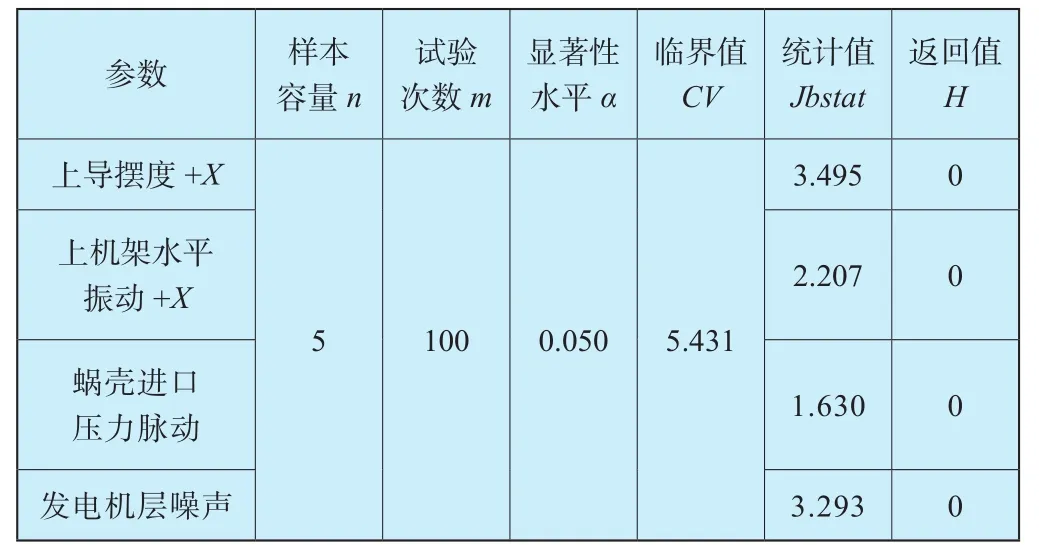
表1 監測參數正態分布檢驗結果Table 1 Test results of Gaussian distribution on monitoring parameters
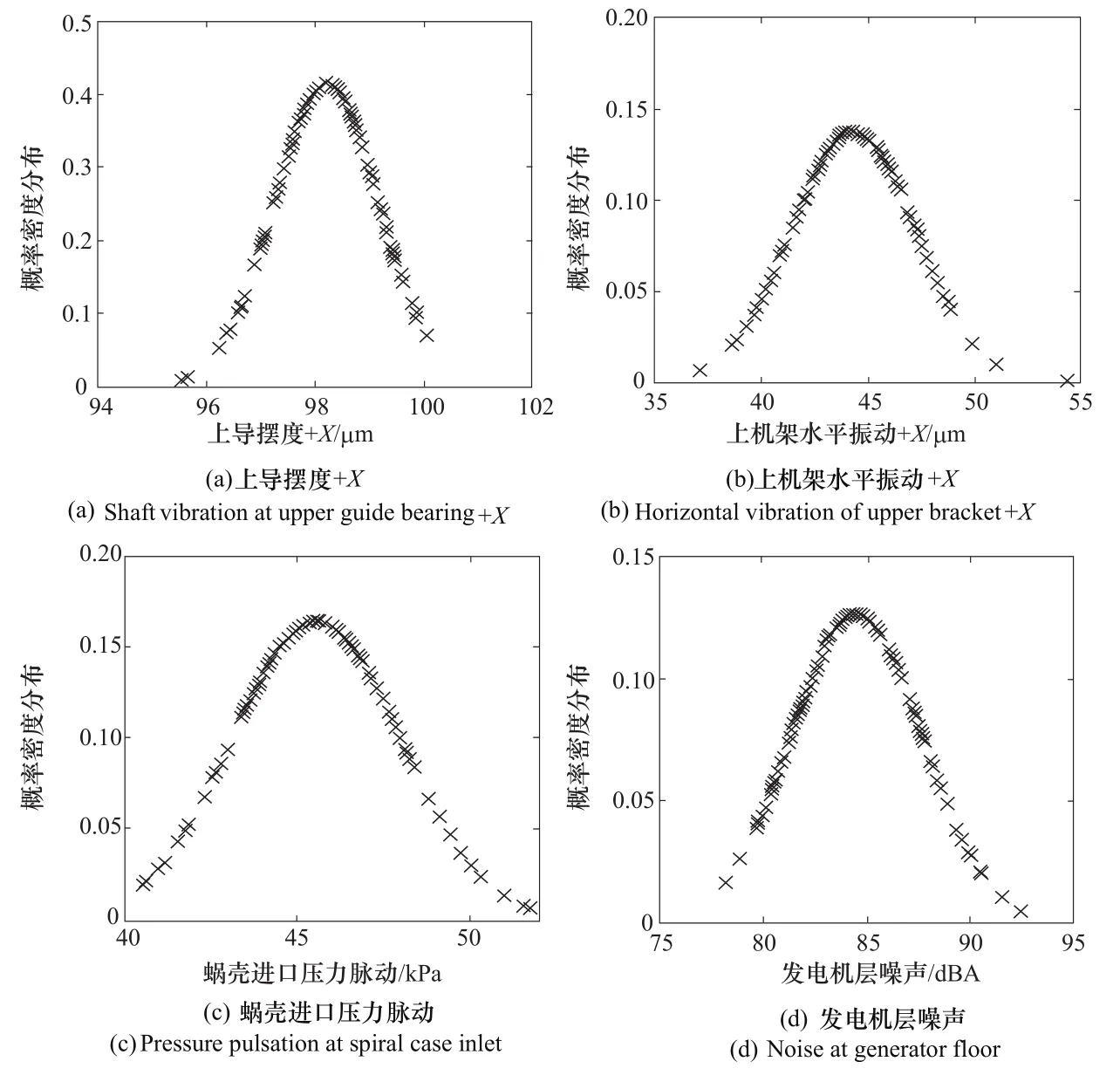
圖2 監測參數概率密度分布圖Figure 2 Probability density distribution of monitoring parameters
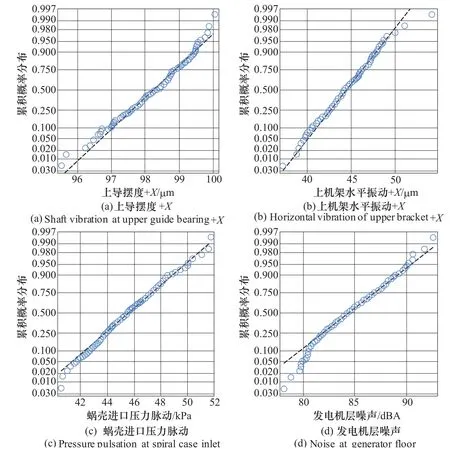
圖3 監測參數累積概率分布圖Figure 3 Cumulative probability distribution of monitoring parameters
表1中,樣本容量n為單次試驗的采樣次數,試驗次數m即樣本均值序列的容量,統計值Jbstat均小于臨界值CV,檢驗返回值H均為0,表明4個監測參數的樣本均值序列均服從正態分布,驗證了檢驗前的預測。樣本均值序列的均值和方差統計同總體的對比如表2所示。
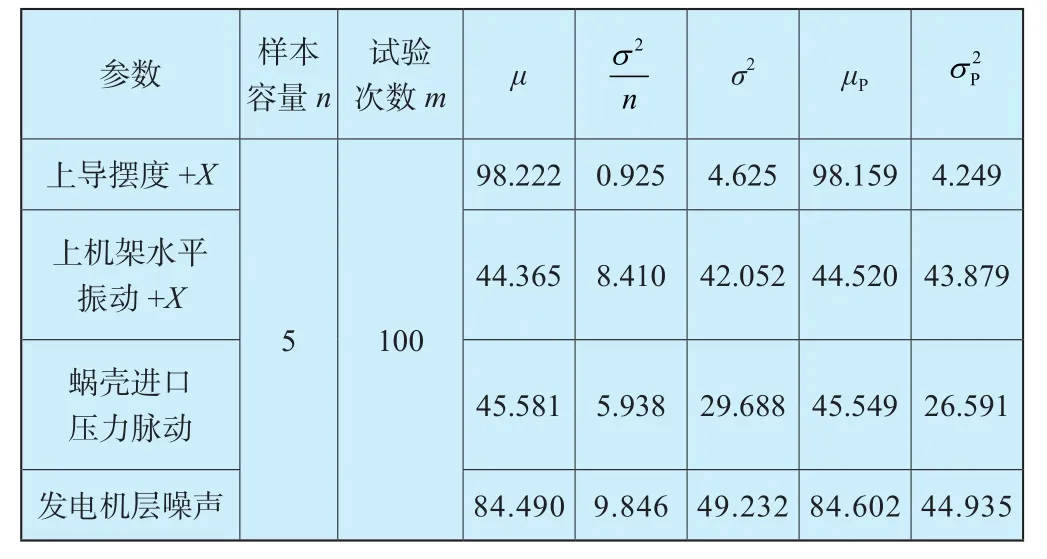
表2 監測參數樣本均值與方差估計結果Table 2 Estimation results of sample average and variance of monitoring parameters
從表2可以看出,由樣本均值推算出的均值μ和方差σ2同實際總體的均值μP和方差較為接近,可以將經過檢驗的樣本均值序列作為波動預警的數據基礎。
2.3 波動預警策略
根據上述檢驗結果,狀態監測參數的樣本均值序列服從正態分布,可利用正態分布的知識對其波動閾值進行規定。根據正態分布理論,服從正態分布的監測量在(μ-3σ,μ+3σ)區間波動的概率為99.74%,可根據3σ準則,即判斷監測量是否位于該區間來判定該監測量是否超出正常的波動范圍,采用該準則可以涵蓋絕大部分的正常數據,能夠滿足工程上的監測需要。
對水電機組狀態監測系統,單一閾值的預警依據往往來源于相關國內、外標準的規定,如擺度預警閾值設定來源于GB/T 11348.5—2002《旋轉機械轉軸徑向振動的測量和評定 第5部分:水力發電廠和泵站機組》,振動預警閾值設定來源于GB/T 8564—2003《水輪發電機組安裝技術規范》等。當監測參數出現小幅波動,尚未超過預設預警閾值時,系統難以發現和做出及時預警。利用正態分布知識對監測參數進行波動預警,可有效地捕捉這一類異常波動。具體實施時,對任一監測參數,當系統采集到最新的實時監測值時,首先判斷其是否超過單一閾值,如超過則馬上作出越限預警;計算最新實時監測值與前序相鄰若干監測值的均值,若超過根據3σ準則預設的波動區間,則做出波動預警。預警流程圖如圖4所示。波動預警的模式,可有效監測參數偶然出現的數值波動,若該波動持續不間斷地發生,且波動量超出預設區間的程度呈現一定的規律性,則可判斷機組存在某種異常,需進行進一步檢查。
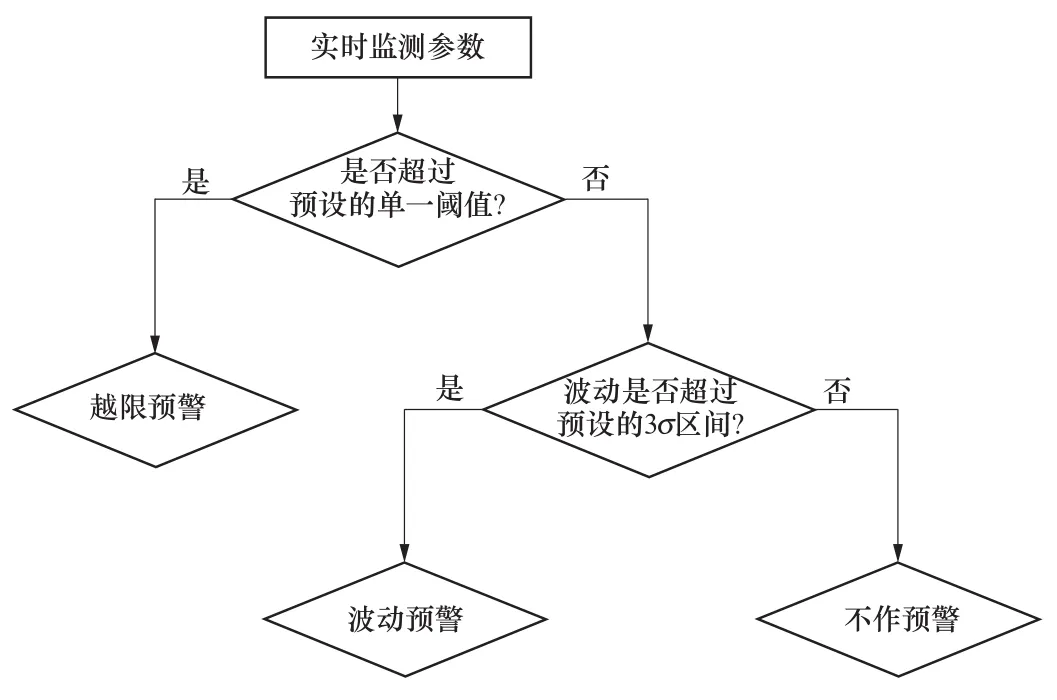
圖4 預警策略流程圖Figure 4 Flow diagram of alarm procedure
3 結論
本文以水電機組的實際監測數據為研究對象,對其樣本均值序列進行了嚴格的分布檢驗,結果表明,樣本均值序列服從正態分布,驗證了中心極限定理的正確性。進而根據正態分布的理論,提出了基于3σ準則的波動預警策略,該預警模式可有效地捕捉狀態監測參數的小幅異常波動,對監測參數的波動量做出及時預警,保障機組在發生小幅變化時可被系統及時察覺,有利于機組的長期安全運行。為防止誤報、錯報發生,本文提出的波動預警策略,仍需得到長期運行的考驗,以不斷完善,實現科學、全面地監測預警。

