Kalman濾波組合預(yù)測模型研究及其在高鐵路基沉降中的應(yīng)用

焦雄風(fēng) 張獻(xiàn)州 蔣英豪 陳 錚 譚社會

(1.西南交通大學(xué)地球科學(xué)與環(huán)境工程學(xué)院,成都 611756; 2.高速鐵路運(yùn)營安全空間信息技術(shù)國家地方聯(lián)合工程實(shí)驗(yàn)室,成都 611756; 3.中國鐵路上海局集團(tuán)有限公司,上海 200071)

1 概述

影響高速鐵路路基沉降的因素較多,建立各影響因素與形變過程之間精確的函數(shù)模型十分關(guān)鍵。已有許多學(xué)者開展相關(guān)研究,毛文飛等研究了改進(jìn)的MEEMD-ARMA殘差修正組合預(yù)測模型[1];岳春芳等將RBF神經(jīng)網(wǎng)絡(luò)組合模型應(yīng)用于GPS高程擬合中[2];楊帆等研究自回歸預(yù)測模型變權(quán)組合定階方法[3]。上述研究表明,組合預(yù)測模型不論是從信息豐度還是預(yù)測效果方面都優(yōu)于單類預(yù)測模型。然而,在每一次預(yù)測計(jì)算時,需要根據(jù)往期先驗(yàn)信息重新調(diào)權(quán),會造成大量計(jì)算冗余。近年來,自適應(yīng)Kalman濾波理論趨于成熟,馮磊等研究自適應(yīng)Kalman濾波在高鐵沉降觀測數(shù)據(jù)處理中的應(yīng)用[4];Christopher等將自適應(yīng)Kalman濾波應(yīng)用于INS/GPS的組合導(dǎo)航中[5];Akbar等基于協(xié)方差采樣提出一種自適應(yīng)卡爾曼濾波模型,并驗(yàn)證了該方法的有效性[6]。基于前人的研究,采用基于極大似然估計(jì)的自適應(yīng)Kalman濾波算法與組合預(yù)測模型進(jìn)行結(jié)合,與目前較為實(shí)用的預(yù)測模型進(jìn)行比較,從擬合情況、精度評判指標(biāo)等方面,探究上述自適應(yīng)kalman濾波組合預(yù)測模型的可靠性。

2 單類因素預(yù)測模型構(gòu)建

2.1 單類因素預(yù)測模型容量選擇

研究表明,并不是囊括越多單類因素預(yù)測模型,其組合預(yù)測模型的精度就越好[7]。相反,如果構(gòu)建的單類預(yù)測模型精度不高,甚至與其他單類預(yù)測模型發(fā)生信息沖突,還會降低組合預(yù)測模型的精度。為了解決上述問題,嘗試采用包容性檢驗(yàn)原理[8]來處理組合預(yù)測模型的容量選擇問題,步驟如下。

假設(shè)w1、w2為兩種不同的單類預(yù)測模型,兩者第t期的預(yù)測值為δ1,t、δ2,t,當(dāng)期實(shí)際變化量為γt時,可表示為

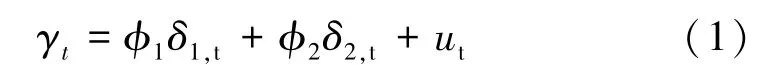
Φ1、Φ2分別表示回歸系數(shù),且兩者之和為1,ut為方程隨機(jī)噪聲。

上式同時減去δ1,t,有

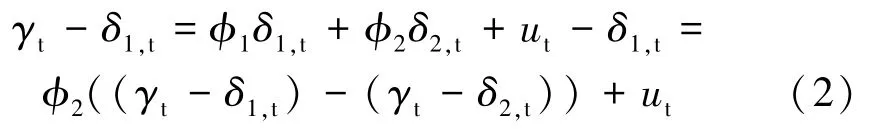
設(shè)εi,t=γt-δi,t(i=1,2),則有

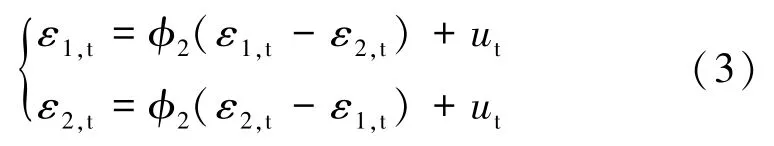
由此,組合預(yù)測模型的容量選擇問題可看作對式(3)的線性假設(shè)的顯著性檢驗(yàn), 給出假設(shè)

(3)當(dāng)Φ1=0,Φ2=1時,則表示w2包容w1,即w2包含w1的信息,w1對組合預(yù)測模型沒有影響,可裁去w1;當(dāng)Φ2=0,Φ1=1時,則表示w1包容w2,即w1包含w2的信息,w2對組合預(yù)測模型沒有影響,可裁去w2。

當(dāng)單類預(yù)測模型推廣到n個時[9],可將其看作第i類單類預(yù)測模型和n-i個單類預(yù)測模型的集合,首先對單類預(yù)測模型進(jìn)行預(yù)測精度評價,然后對其預(yù)測效果進(jìn)行排序,基于上述兩種單類預(yù)測模型包容性檢驗(yàn)的思想,對單類預(yù)測模型逐個檢驗(yàn),最后得到1組效果最優(yōu)的組合預(yù)測模型。

2.2 單類因素預(yù)模型定權(quán)

建立組合預(yù)測模型正確與否取決于兩大核心問題:①單類模型的正確選擇;②單類預(yù)測模型的權(quán)重。針對第二點(diǎn),采用熵值法進(jìn)行權(quán)重賦予。

利用熵值法對單類預(yù)測模型賦權(quán),λit為單類預(yù)測模型相對誤差,有

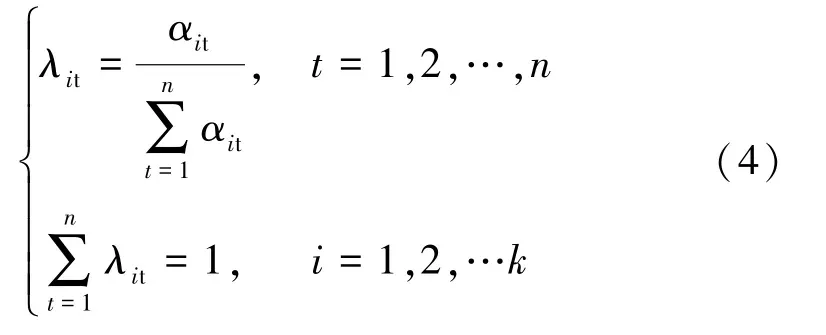
αit表示t期第i類預(yù)測模型的預(yù)測相對誤差值,其取值如下

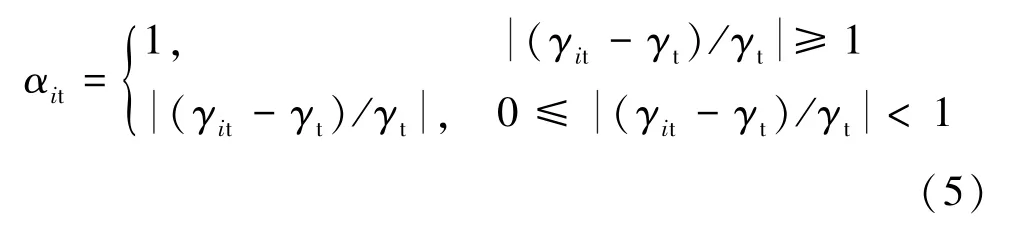
3 改進(jìn)Kalman濾波

3.1 基于極大似然估計(jì)的自適應(yīng)Kalman濾波

標(biāo)準(zhǔn)Kalman濾波函數(shù)模型為:

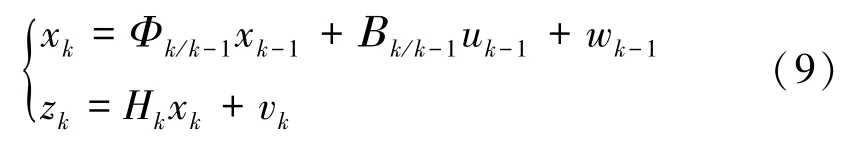
其中,xk為(n×1)初值參數(shù)矩陣;zk為(m×1)監(jiān)測參數(shù)矩陣;wk為(n×1)動態(tài)噪聲;vk為(m×1)監(jiān)測噪聲;Φk/k-1為(n×n)狀態(tài)轉(zhuǎn)移矩陣;Hk為(m×n)觀測矩陣;Bk/k-1為(n×r)控制參數(shù)的增益矩陣;uk-1為(r×1)控制參數(shù)矩陣;下標(biāo)k為第k時刻在某一時刻的估值,可按如下公式遞推演算得到。

狀態(tài)值及估計(jì)協(xié)方差矩陣一步預(yù)測為

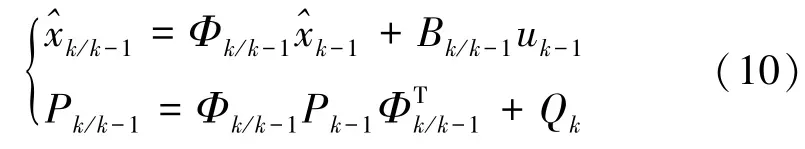
測量誤差、測量誤差協(xié)方差及最優(yōu)卡爾曼增益一步更新為

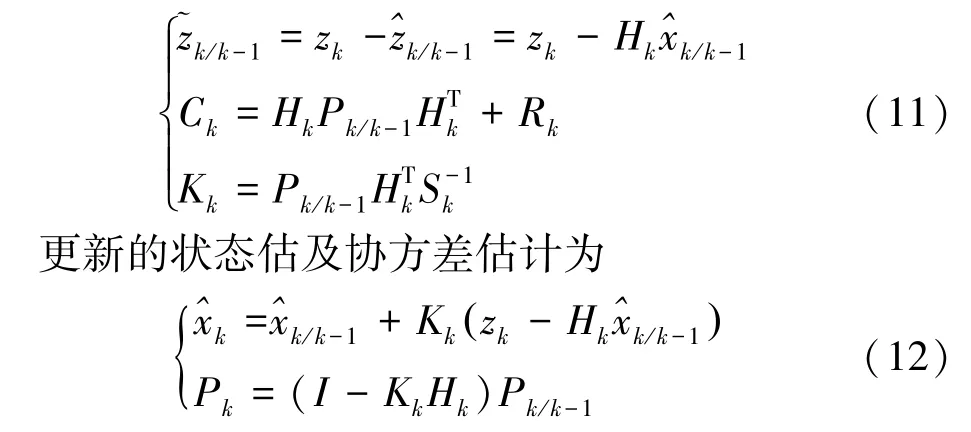
通過上述公式遞推流程,若給定初值狀態(tài)參數(shù)以及在k時刻下的觀測值Zk,就能得到在k時刻下目標(biāo)狀態(tài)的一步預(yù)報(bào)值

上述標(biāo)準(zhǔn)Kalman濾波中的Q和R都為固定參數(shù),無法隨著預(yù)測誤差的變化動態(tài)調(diào)整,有學(xué)者提出一種基于極大似然估計(jì)理論的自適應(yīng)Kalman濾波[10],從系統(tǒng)測量出現(xiàn)概率最大的方面來預(yù)測,不但可以追蹤預(yù)測誤差變化,還可以捕捉預(yù)測誤差的協(xié)方陣變化[11]。其自適應(yīng)性體現(xiàn)在系統(tǒng)噪聲協(xié)方差陣Q和觀測噪聲協(xié)方差陣R的實(shí)時修正[12],主要通過基于預(yù)測

式中,tr表示對矩陣求逆。由此,對Q、R的修正問題轉(zhuǎn)變?yōu)閷?shù)α求導(dǎo)的問題。

根據(jù)標(biāo)準(zhǔn)Kalman濾波基本方程,有

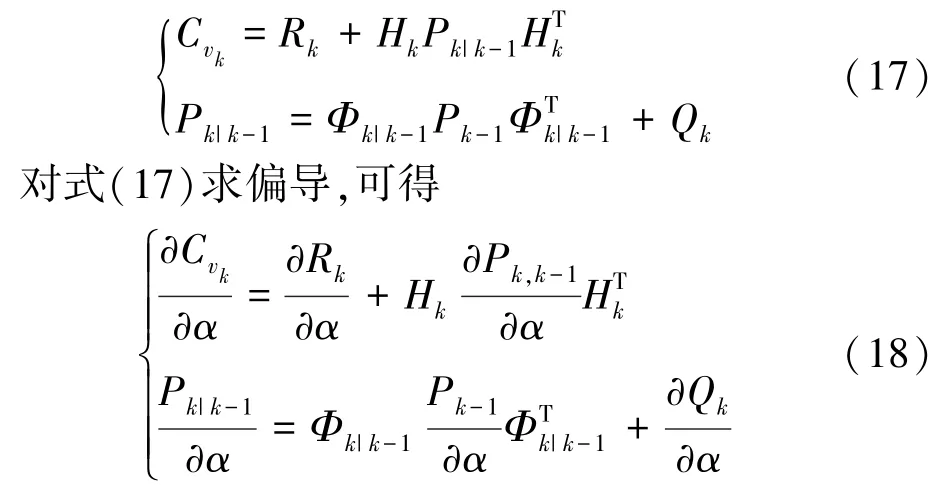
假設(shè)濾波處于穩(wěn)態(tài)時,狀態(tài)誤差的方差陣Pk-1理論上無限接近某常量,有

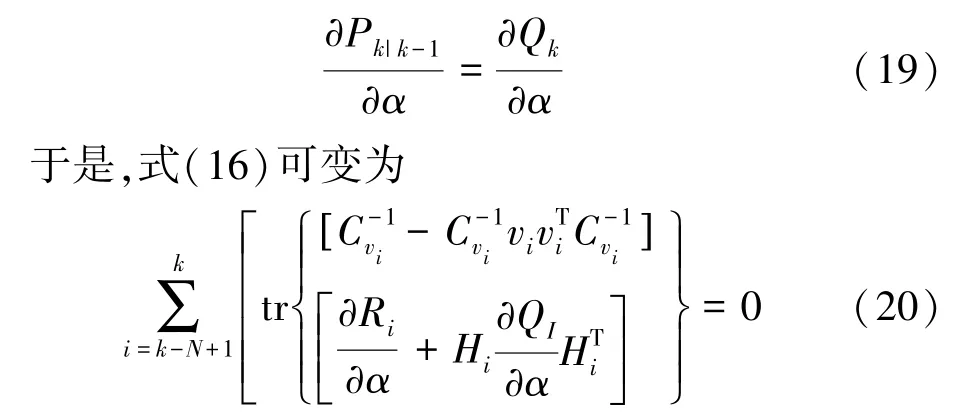
通過上述公式,可以求得α的實(shí)時估計(jì),進(jìn)而可以對Q、R進(jìn)行實(shí)時修正。

3.2 噪聲協(xié)方差矩陣的幾種修正方式

(1)測量噪聲協(xié)方差矩R修正

假設(shè)系統(tǒng)噪聲協(xié)方差陣Q已知,式(20)可以簡化為

(3)噪聲協(xié)方差陣Q、R同步修正

通過上述修正方式可以看到,當(dāng)對其中1個噪聲協(xié)方差陣進(jìn)行調(diào)整時,必須假設(shè)另1個為已知量,即兩者必須有1個作為已知量。同步調(diào)整2個噪聲協(xié)方差陣時,若不考慮已知信息,則可能導(dǎo)致式(21)、式(24)不成立[15],繼而導(dǎo)致濾波穩(wěn)態(tài)喪失,達(dá)不到所要求的自適應(yīng)性。故應(yīng)慎重考慮同時對Q、R的同步修正。

4 基于極大似然估計(jì)的自適應(yīng)Kalman濾波組合預(yù)測模型

4.1 組合預(yù)測模型建立

一般情況下,對同一觀測值,假設(shè)用m種單類預(yù)測模型預(yù)測,其組合預(yù)測模型為

例如某種變形量與溫度、時間因子的組合預(yù)測模型[16],有

式(29)、式(30)建立后,即可用基于極大似然估計(jì)的自適應(yīng)Kalman濾波算法進(jìn)行推算。

4.2 模型預(yù)測精度評價指標(biāo)

引入Pearson相關(guān)系數(shù)、相關(guān)指數(shù)R2、均方根誤差RMSE[17]、平均絕對誤差MAE來進(jìn)行相關(guān)性分析及模型預(yù)測精度評價,pearson能衡量兩變量之間是否存在線性相關(guān)關(guān)系,其值越接近1,表示兩者相關(guān)性越強(qiáng);R2能衡量模型回歸效果,其值越接近1,表示回歸效果越顯著;RMSE能反映估值與監(jiān)測值之間的偏差,其值越小表明其模型預(yù)測精度越好;MAE能反映估值誤差的實(shí)際情況,其值越小,表明模型擬合程度越高,公式為

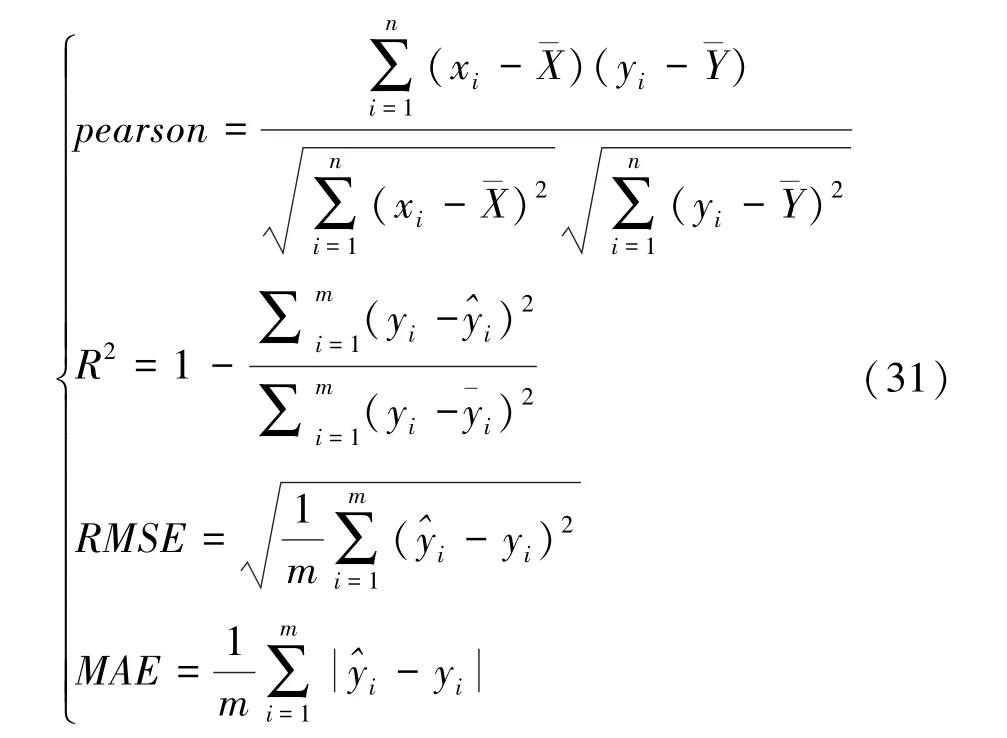
式中,m為觀測期數(shù);表示模型估計(jì)值表示觀測量平均值;yi、xi表示實(shí)際觀測量。

5 實(shí)例分析

5.1 高速鐵路路基沉降監(jiān)測數(shù)據(jù)分析

(1)工程概況

某高速鐵路路基區(qū)段,長1.916km,共26個觀測斷面,每個觀測斷面在上下行各設(shè)1個路基觀測樁進(jìn)行監(jiān)測,路基填筑完成時間為2018年12月31日,利用高精度水準(zhǔn)儀及精密水準(zhǔn)尺進(jìn)行若干次的周期性重復(fù)測量,監(jiān)測內(nèi)外業(yè)精度均符合相關(guān)規(guī)定。

(2) 數(shù)據(jù)分析

現(xiàn)對該路基的小里程段、中里程段、大里段各挑選1個觀測斷面,選取2016年6月至2019年12月對應(yīng)的上行路基觀測樁 0085880L1、0086686L1、0087492L1監(jiān)測數(shù)據(jù)(共180期)進(jìn)行分析,數(shù)據(jù)如圖1所示。

由圖1可知,3個斷面路基觀測樁的監(jiān)測數(shù)據(jù)都表現(xiàn)為逐漸沉降且趨于穩(wěn)定。

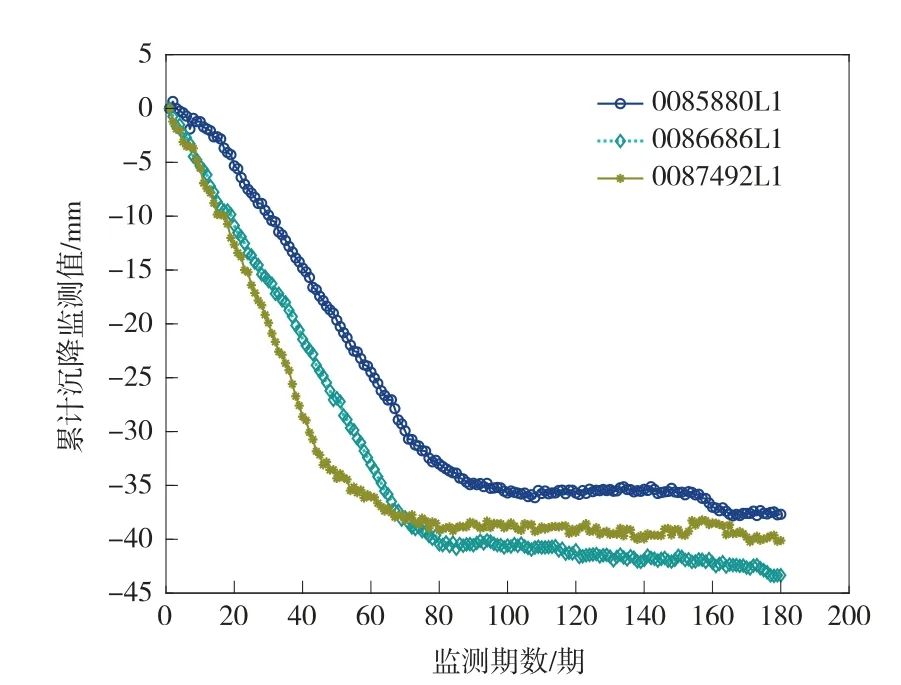
圖1 累計(jì)沉降監(jiān)測數(shù)據(jù)

路基沉降主要受外力荷載的影響,堆載預(yù)壓都會使路基隨時間發(fā)生一定程度的沉降。另外,還需要考慮荷載作用次數(shù)及地質(zhì)類型等,這類參數(shù)因子難以量化,而通過路基填筑平均高度及時間的變化來建立路基沉降預(yù)測模型,可定量分析具體沉降趨勢。

5.2 單類預(yù)測模型建立

路基沉降擬合預(yù)測常用方法有雙曲線法、三點(diǎn)法、泊松曲線法等,這些方法均考慮以時間因子為自變量,累計(jì)沉降量為因變量,即沉降隨時間發(fā)生變化。因此,根據(jù)上述3個監(jiān)測樁的沉降趨勢,提出6種以時間因子為自變量的預(yù)測模型,有

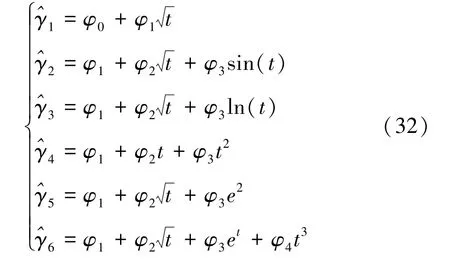
式中,分別表示基于時間因子的模型預(yù)測值;t為以天為單位數(shù)值化的時間因子;φi表示模型回歸參數(shù)。

為篩選出最優(yōu)預(yù)測模型,以前120期的監(jiān)測數(shù)據(jù)為建模樣本,預(yù)測后一期的累計(jì)沉降量,有關(guān)精度分析情況如圖2、表1所示。

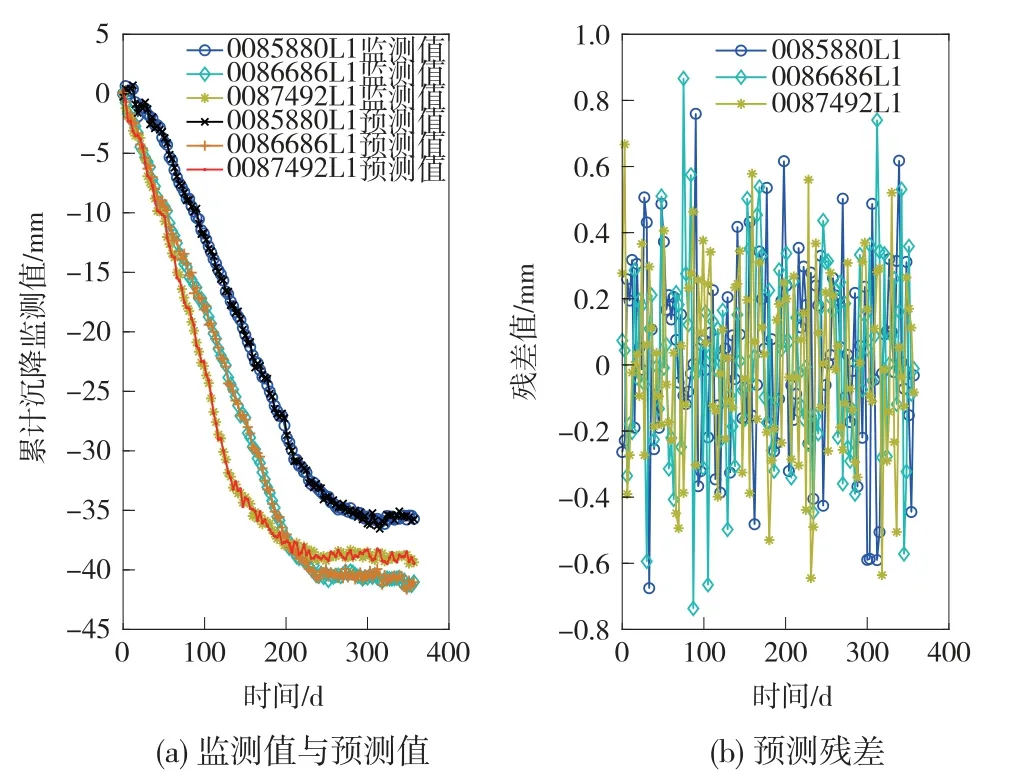
圖2 基于時間因子的單類模型預(yù)測結(jié)果及殘差

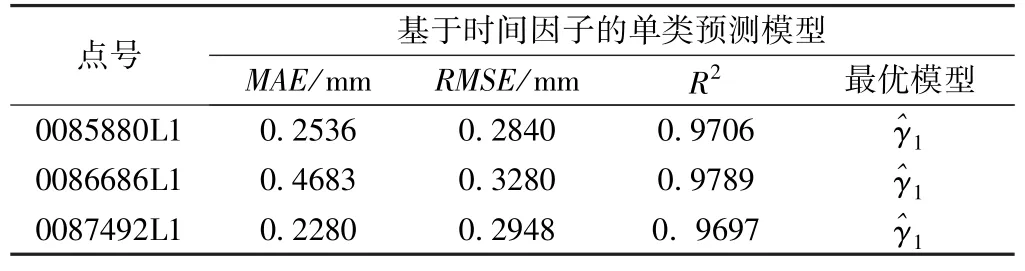
表1 精度評價指標(biāo)

為判斷路基填筑平均高度與路基樁沉降是否具有強(qiáng)相關(guān)性,取監(jiān)測當(dāng)日、前15d、前30d和前45d的路基填筑平均高度與當(dāng)日路基觀測樁沉降量的pearson相關(guān)系數(shù),如表2所示。

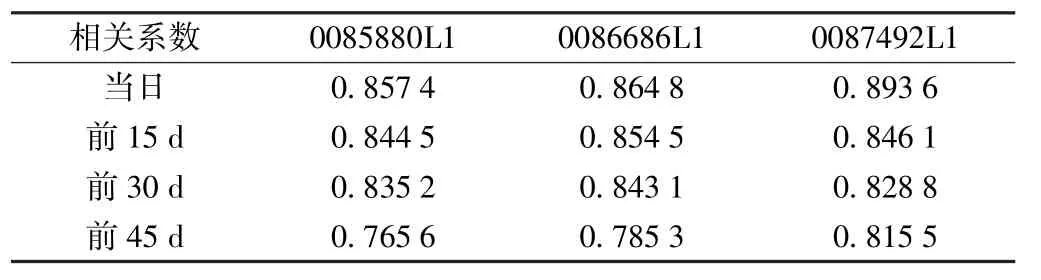
表2 pearson相關(guān)系數(shù)

由表2可知,該段路基填筑平均高度變化與路基樁沉降量存在強(qiáng)線性相關(guān)。取監(jiān)測當(dāng)日、前15d、前30d、前45d的路基填筑平均高度作為自變量,預(yù)先構(gòu)建線性模型,有

式中,分別表示基于路基填筑平均高度的模型預(yù)測值,μi表示回歸參數(shù)。θi表示監(jiān)測當(dāng)日的前i天的路基填筑平均高度。

選擇與基于時間因子預(yù)測模型同樣的數(shù)據(jù)進(jìn)行計(jì)算,結(jié)果如圖3、表3所示。

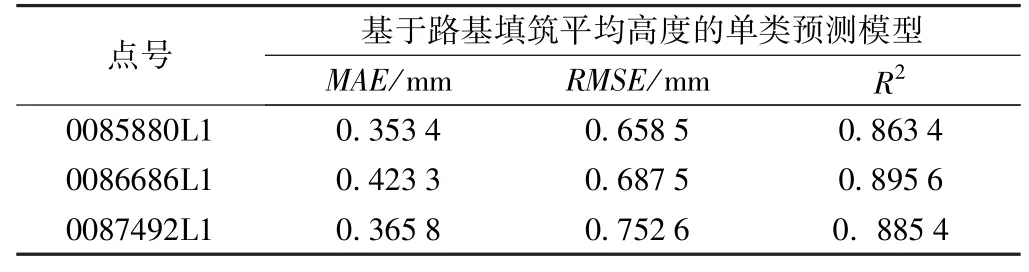
表3 精度評價指標(biāo)

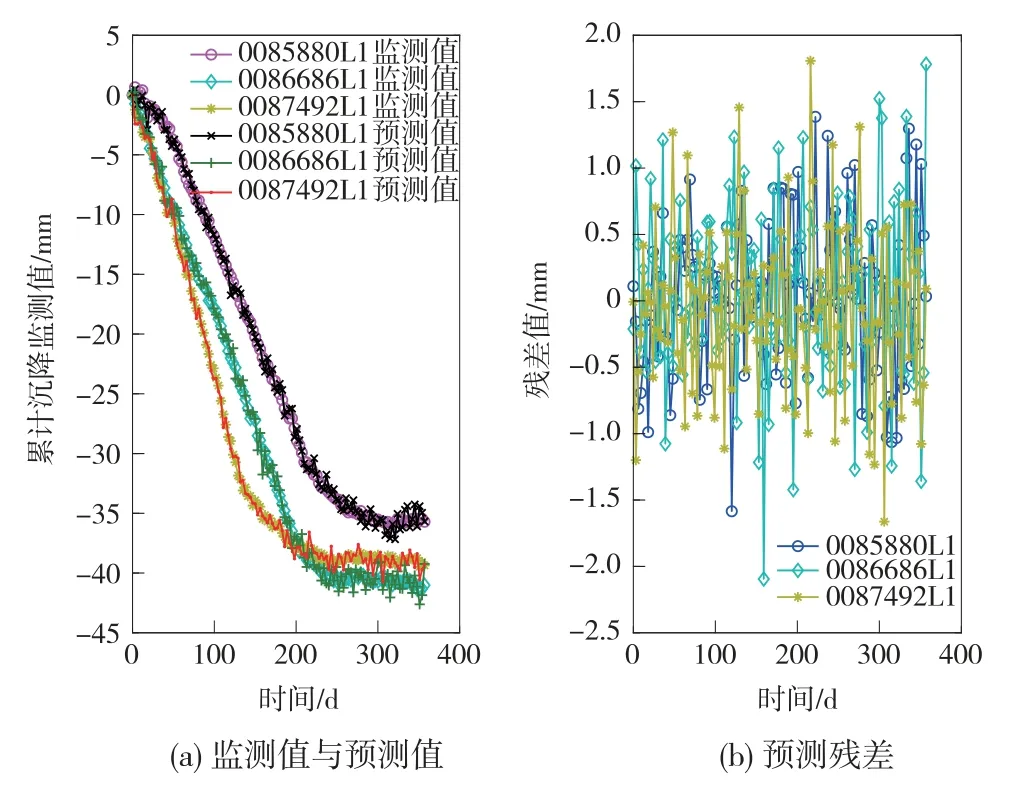
圖3 基于路基填筑平均高度的單類模型預(yù)測結(jié)果及殘差

確定上述單類預(yù)測模型具體參數(shù)后,利用2.1節(jié)的包容性檢驗(yàn)原理對兩個單類預(yù)測模型之間的信息包含程度進(jìn)行分析,取顯著性水平α=0.025,經(jīng)計(jì)算,3個點(diǎn)0085880L1、0086686L1、0087492L1的t統(tǒng)計(jì)量分別為4.054、4.5823、4.2359,由此可見,t0.0025(58)=2.0017,原假設(shè)不成立,即單類預(yù)測模型可組合。

組合預(yù)測中的單類預(yù)測模型容量確定后,再利用熵值法對兩單類預(yù)測模型進(jìn)行定權(quán),取第前119期的兩單類預(yù)測數(shù)據(jù)作為計(jì)算數(shù)據(jù),求得120期數(shù)據(jù)的各單類模型權(quán)值,結(jié)果如表4所示。

表4 單類模型權(quán)值分配情況

5.3 模型預(yù)測分析

當(dāng)上述組合預(yù)測模型確定后,即可利用基于極大似然估計(jì)的自適應(yīng)Kalman濾波進(jìn)行濾波推估,取組合預(yù)測模型第120期的預(yù)測模型參數(shù)為狀態(tài)參數(shù)初值,取初始估計(jì)協(xié)方差矩陣P0為I(單位矩陣),考慮組合預(yù)測系統(tǒng)的估計(jì)誤差,采用2.3節(jié)的第二種方差調(diào)整方式進(jìn)行自適應(yīng)調(diào)整,系統(tǒng)噪聲協(xié)方差矩陣Q=1、觀測噪聲協(xié)方差矩陣取R=0.01,為對所提出組合預(yù)測方法性能進(jìn)行客觀評價,增加基于非等間隔灰色系統(tǒng)的最優(yōu)權(quán)組合預(yù)測模型進(jìn)行對比實(shí)驗(yàn),計(jì)算結(jié)果及精度評價如圖4、表5所示。

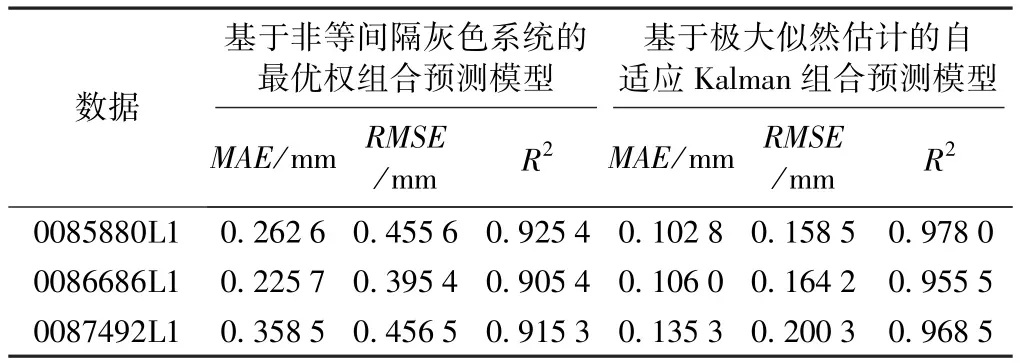
表5 精度評價指標(biāo)

由圖4、表5可知,基于非等間隔灰色系統(tǒng)的最優(yōu)權(quán)組合預(yù)測模型的平均絕對誤差、均方根誤差、相關(guān)指數(shù)最優(yōu)精度分別為0.2257mm、0.3954mm、0.9254;基于極大似然估計(jì)的自適應(yīng)Kalman組合預(yù)測模型的平均絕對誤差、均方根誤差、相關(guān)指數(shù)最優(yōu)精度分別為0.1028mm、0.1585mm、0.9780。實(shí)驗(yàn)表明,基于極大似然估計(jì)的自適應(yīng)Kalman組合預(yù)測模型各項(xiàng)精度指標(biāo)皆優(yōu)于基于非等間隔灰色系統(tǒng)的最優(yōu)權(quán)組合預(yù)測模型。由此可見,在對單類預(yù)測模型加權(quán)組合后,其預(yù)測精度得到了提高,而結(jié)合自適應(yīng)Kalman濾波,可進(jìn)一步增強(qiáng)組合預(yù)測模型的自適應(yīng)性。

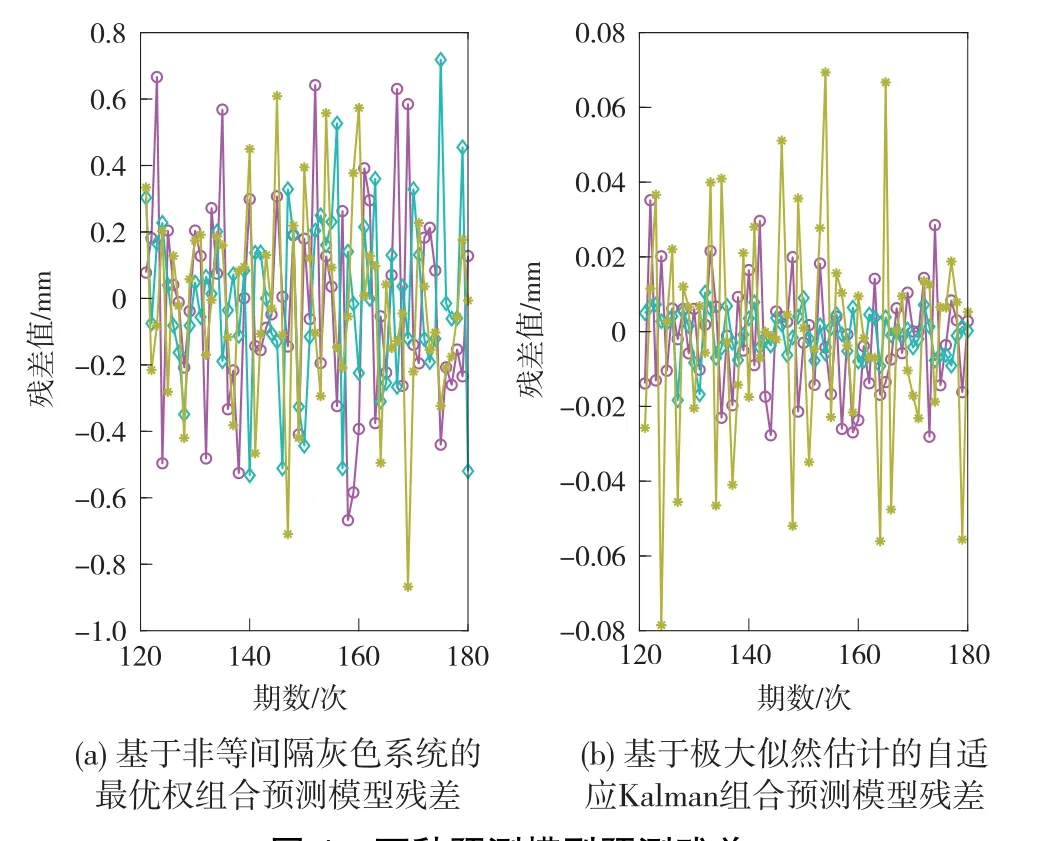
圖4 兩種預(yù)測模型預(yù)測殘差

6 結(jié)語

建立組合預(yù)測模型來分析高速鐵路路基沉降監(jiān)測數(shù)據(jù)十分必要,上述研究表明,組合預(yù)測手段能在一定程度上改善預(yù)測精度,結(jié)合基于極大似然估計(jì)的自適應(yīng)Kalman濾波算法,利用其只需一定的初始參數(shù),就能自動更新迭代,且在更新的過程中不斷對噪聲方差進(jìn)行修正的自適應(yīng)特性,可解決組合預(yù)測模型中冗余計(jì)算等問題,有效減少組合預(yù)測模型誤差的積累,提高組合預(yù)測模型的自適應(yīng)能力。但上述模型只考慮2種單類預(yù)測模型的組合問題,而現(xiàn)實(shí)中其他環(huán)境因素的并沒有考慮,需要進(jìn)行深入研究。