具有干擾抑制的電液伺服系統控制器設計

常景嵐，張高峰，曹秀芳，楊秀萍*，王收軍

（1.天津理工大學a.天津市先進機電系統設計與智能控制重點實驗室，b.機電工程國家級實驗教學示范中心，天津300384；2.南京晨光集團有限責任公司，南京210006）

電液伺服系統由于具備響應快、精度高、維護方便、傳動效率高等優點被廣泛應用在航空航天、軍工、礦山機械、冶金煉金等領域[1]。然而電液伺服系統作為典型的傳動系統，其控制精度受到建模不完整和非線性因素的影響[2]，這就對其控制策略提出了很高的要求。

為了提高電液伺服系統的控制精度，文獻[3]建立了盡可能詳細的電液系統模型，運用自適應魯棒控制策略。在此基礎上，文獻[4]使用濾波器來避免虛擬控制器中的復雜微分項，但其只依靠非線性反饋項來處理模型中各種不確定性，獲得的控制性能只能在較小干擾下保持。文獻[5]采用有限時間滑模控制，但無法消除不匹配干擾對于系統控制性能的影響。觀測器理論上可以對系統中未知干擾進行估計，從而提高系統抗干擾能力[6-7]。文獻[8]設計了非線性觀測器，但其采用的魯棒控制法需要依靠很大的反饋增益來保證系統穩定性，而過大的反饋增益會導致系統控制器在設計初時的一些前提條件被破壞，進而使系統發散。

因此，本文針對電液伺服系統高度非線性和模型不確定性的特點，設計了一個不匹配干擾來描述系統的模型誤差，建立了考慮摩擦以及不匹配干擾的閥控缸數學模型。通過設計觀測器來預測系統中存在的不匹配干擾，使用基于參數映射的自適應律處理系統中的不確定參數，同時由非線性反饋項抑制誤差造成的影響。本文設計的控制器可以有效抑制不匹配干擾對系統的影響，減少控制器對于高增益反饋的依賴，顯著提高系統的控制精度。

1 電液系統模型的建立

如圖1所示的電液伺服系統，其運動學方程為

圖1 單桿活塞缸電液伺服系統Fig.1 Electro-hydraulic servo system of single rod piston cylinder

式中：m為負載質量；y為液壓缸輸出位移；p1、p2為液壓缸左右兩腔壓力；A1、A2為液壓缸左右兩腔活塞的工作面積；B、Af、、d（x，t）分別為黏性阻尼系數、庫侖摩擦系數、類似庫侖摩擦形狀的函數、建模誤差和模型中未建立部分。

對于液壓缸兩腔的壓力：

式中：V1、V2分別為液壓缸左右兩腔實際容積；E為液壓油彈性模量；Ct為液壓缸泄露系數；pL=p1-p2為液壓缸左右兩腔壓差；q1、q2分別為伺服閥流入和流出液壓缸左右兩腔的流量。

假設1：伺服閥對稱匹配，伺服閥頻寬遠大于系統頻寬，且0＜pr＜p1＜ps，0＜pr＜p2＜ps，則對于伺服閥流量有

式中：g為伺服閥控制流量增益；u為系統控制輸入；ps、pr為供油端壓力和回油端壓力；s（u）=

由式（1）定義系統狀態變量為：x=[x1，x2，x3]T=

假設2：對于未知參數φ、建模誤差和未建模部分，其范圍已知

其中：φmin=[φ1min，φ2min，φ3min]T，φmax=[φ1max，φ2max，φ3max]T分別為向量φ的下界和上界；δd為已知有界函數。

假設3：系統參考的指令信號x1d（t）三階連續有界。

2 控制器設計

首先將式（4）中的d（x，t）擴張為冗余狀態xe，并令xe=-d（x，t）/m，則x˙e=h（t），于是式（4）擴張后的系統狀態方程為

基于式（6）的設計觀測器為

其中·i表示向量·中的第i個元素。定義如下自適應律：

式中：Γ＞0為自適應增益，是一個正定對角矩陣；τ為自適應函數。通過分析式可知，參數的范圍可控，且相同于式（5）中φ的范圍，可得出如下性質：

定義下面誤差變量：

式中：e1表示系統跟蹤誤差。

由式（4）、（11）可得

為了使e2趨于0，將x3看做式（12）中的一個控制輸入，并設計控制函數α2

式中：k2s1為控制器參數，且k2s1＞0；α2a是模型補償項；α2b為系統線性穩定反饋；α2c為非線性反饋。

定義e3=x3-α2，則由式（12）、（13）得：

其中：η2T=[-x2，-Sf（x2），0]，選擇合適的α2c從而滿足如下條件：

式中：σ1為大于零的控制器設計參數；k2s2＞0為非線性反饋增益[2]。

由e3定義以及式（4）得知

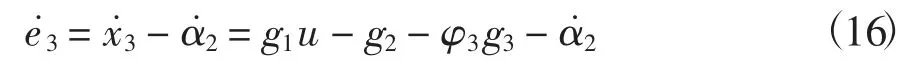
通過分析α˙2可知，它包括可計算的偏微分部分和不可計算的部分，因此將兩者分別歸為α2d和α2e。

由式（16）、（17）可得控制器u結構如下

式中：k3s1為控制器參數，且k3s1＞0；ua是模型補償項；ub為系統線性穩定反饋；uc為非線性反饋。

將式（18）代入式（16）可得

式中：σ2為大于零的控制器設計參數；k3s2＞0為非線性反饋增益[2]。

3 控制器性能分析

綜合設計參數k1，k2s1，k3s1，使下面矩陣Λ為正定矩陣：

定理：令自適應函數τ=η2e2+η3e3，設計的控制器u具有如下性質：

①系統中所有信號皆為有界信號；

證明：對于定理①設置如下Lyapunov函數

對式（22）Lyapunov函數微分，結合式（11）、式（14）、式（19）可得

根據式（15）、式（20）和正定矩陣Λ可得

式中：ρ=2λmin（Λ）μ；λmin（Λ）為矩陣Λ的最小特征值；μ為向量中最小的元素；σ=σ1+σ2。

對式（24）解微分不等式可得

由式（25）可得出V是有界的，結合式（22）可證明定理①。

根據式（15）、式（20），可得

根據式（9）以及自適應函數Γ=η2e2+η3e3，可得

根據式（10），可得

式中K∈Lp，p=2[9]。對K求導，結合式（11）、式（14）、式（19）并由定理①得知，K˙有界。根據Barbalat引理，由文獻[9]中引理5可知，再由λmin（Λ）＞0可知，

4 仿真驗證

在Matlab中搭建系統模型驗證本文提出的控制策略的有效性，為使得模型更加接近實際情況，系統參數參考文獻[10]的表4：B=4 000 N·s/m；Af=119 N；Ct=7×10-12m5/（N·s）；E=7×108Pa；A1=12.56×10-4m2；A2=9.42×10-4m2；Sf=2arctan（1 000x2）/π；Ps=8×106Pa；Pr=0 Pa；g=7×

取下面3種控制策略進行仿真對比。

1）基于擴張狀態觀測器的自適應魯棒控制器（extended state observer adaptive robust controller，ESOARC）。控制系統參數為：k1=200；k2s1+k2s2=160；k3s1+k3s2=80；φmin=[3 970，90，4×10-12]；φmax=[4 030，130，1×10-11]；φ（0）=[3 970，90，4×10-12]；自適應增益Γ=diag[50，20，1×10-25]；觀測器參數ω0=1 000。

2）自適應魯棒控制器（adaptive robust controller，ARC）。不包含干擾估計部分，其他參數與ESOARC控制器相同。

3）PID（proportion integration differentiation）控制器。控制器參數為kp=1 500，ki=600，kd=0。

工作條件如下：最大運動速度為15 mm/s；頻率為0.5 Hz；系統外部干擾d（x，t）=50 sin（πt）；在10 s時添加持續10 s的階躍干擾d（x，t）=50 sin（πt）+100，以檢測系統的抗干擾能力。仿真時間30 s，設定仿真中指令信號為：x1d=0.015 sin（πt）/π。

仿真指令信號如圖2所示。分析圖3，PID控制器在0～10 s和20～30 s期間的跟蹤誤差達到（±8）mm，在10～20 s間由于階躍干擾的影響誤差出現較大的波動，達到了（±23）mm。由此看出：強干擾對于PID控制器的影響較大，其魯棒性較差；ARC控制器跟蹤誤差較PID控制器有很大改善，但其跟蹤精度仍不理想，受階躍干擾的影響較大，且通過圖4可知，自適應過程由于被強干擾污染導致參數估計失效；而本文設計的ESOARC控制器全程都保持較好的跟蹤性能。由圖5可知，觀測器可以準確對干擾進行預測，并在系統控制器中進行補償，使得控制器在強干擾作用下依然保持很好的魯棒性。通過圖6可知，雖然階躍干擾對自適應過程產生了影響，但參數估計仍然保持穩定并向真實值靠近。通過圖7可以看出，相比于PID控制器和ARC控制器，ESOARC控制器的控制信號更加平滑，更有利于在實際系統中實施。

圖2 指令信號Fig.2 Reference signal

圖3 跟蹤誤差Fig.3 Tracking error

圖4 ARC參數估計Fig.4 ARC parameter estimation

圖5 干擾估計Fig.5 Disturbance estimation

圖6 ESOARC參數估計Fig.6 ESOARC parameter estimation

圖7 控制輸入Fig.7 Control input

5 結論

本文針對電液伺服系統存在高度非線性以及模型不確定性的特點，將觀測器和采用反步法設計的自適應魯棒控制器相融合，其中：觀測器對系統中存在的不匹配干擾進行估計，在系統控制器中前饋補償；自適應魯棒控制器通過自適應律得出未知參數的估計值，由不連續參數映射約束參數估計值的范圍，在控制器中用作模型補償；由非線性反饋項抑制不匹配干擾估計誤差和參數估計誤差對系統的影響。利用Lyapunov定理驗證了控制器的性能，并在Matlab仿真中測試了控制器在階躍干擾下的控制性能。結果表明，與PID控制器和ARC控制器相比，ESOARC控制器能有效抑制非匹配干擾對系統的影響，提高了系統的控制精度。