氮化硅陶瓷軸承外圈磨削的雙目標工藝優化*

謝天舒

(包頭鋼鐵職業技術學院 機械工程系， 內蒙古 包頭 014010)

軸承作為關鍵的基礎部件之一，對高端裝備制造具有重要影響。通常要求其具有高強度、高精度、高承載能力、高轉速、高可靠性等重要特性[1]，傳統的金屬軸承逐漸滿足不了日益提高的應用需求。工程陶瓷具有高強度、高硬度、低熱膨脹系數、耐磨損以及耐腐蝕等優良特性，被廣泛應用于精密機械、航空航天、極端工況和軍事設備等重要領域[2-3]。因此，將工程陶瓷材料引入軸承中可大幅提升軸承的服役性能和應用范圍。

工程陶瓷作為典型的硬脆材料，其自身特性決定了磨削為其主要加工方式。但磨削過程中因磨削力較大、磨削熱較多，極易造成陶瓷表面的加工損傷和精度差等問題[4-5]，因此，加工中應選用合理的工藝對加工質量進行控制。軸承外圈作為軸承主要的組成部件之一，其溝道的加工質量對裝配后精度具有重要影響。而外圈溝道的表面粗糙度和圓度作為評價加工表面質量和加工精度的重要指標，對軸承的耐磨性、抗疲勞性、回轉精度、使用壽命等具有很大影響[6-7]。

近年來，國內外學者對陶瓷軸承套圈磨削工藝進行了大量研究。閆海鵬等[8]通過正交試驗對陶瓷內圓磨削表面粗糙度進行了研究，分析了不同工藝參數與表面粗糙度的關系，并在此基礎上建立了氮化硅陶瓷內圓磨削的粗糙度預測模型。郝慧靈[9]研究了氮化硅陶瓷軸承套圈磨削時的磨削力與表面質量關系，從力的角度闡述了磨削工藝參數對表面粗糙度的影響規律。孫長青等[10]研究了砂輪粒度和工藝參數對陶瓷軸承外圈內表面粗糙度的影響規律，通過正交試驗得出了最優工藝參數組合。吳玉厚等[11]對高速電主軸用陶瓷軸承套圈內表面進行了磨削試驗研究，得出了工藝參數對表面粗糙度的影響規律和比磨削能與去除方式的關系，指出在脆性去除時所消耗的能量比塑性去除少。李頌華等[12]采用切入式溝道磨削，研究了工藝參數對氧化鋯陶瓷溝道表面質量的影響規律和加工過程中材料的去除機理，通過試驗得出適當提高磨削深度、增加磨削熱量有利于降低工件表面粗糙度，選用半徑較大的金剛石砂輪加工有助于軸承自潤滑。SUN等[13]研究了工藝參數對氮化硅陶瓷軸承內圓磨削表面形貌的影響規律，通過正交試驗得出最優表面質量的工藝參數，并分析了其去除機理。王強[14]建立了陶瓷軸承套圈表面粗糙度的磨削優化函數，并通過試驗驗證了優化函數的準確性。陳士超[15]通過磨削試驗建立了氧化鋯陶瓷主軸磨削和軸承外圈磨削時的表面粗糙度預測模型，后將預測模型應用于算法優化的目標函數中來指導實際加工。吳玉厚等[16]對氮化硅陶瓷軸承套圈溝道超精加工進行了工藝參數優化研究，得出最優工藝參數組合下超精加工后的軸承套圈溝道表面粗糙度改善率為90.8%。張珂等[7]通過ABAQUS有限元仿真和試驗結合的方式研究了氮化硅陶瓷軸承套圈的超精加工，通過改變不同加工工藝參數, 分析了溝道表面應力分布情況，最終得到了低溝道圓度的工藝參數優化組合。

以上研究表明陶瓷軸承套圈加工工藝對套圈的加工質量具有重要影響，但以往的研究只是單方面關注工藝參數對表面粗糙度或者溝道圓度的影響，沒有將二者同時考慮進去。要同時保證粗糙度和圓度最優，傳統的正交試驗方法無法完成。因此，以工程陶瓷材料中最適合作為軸承的氮化硅陶瓷為研究對象，通過雙目標優化獲得最優加工工藝參數，以期為工程陶瓷實際加工提供技術參考。

1 PSO算法與試驗條件

1.1 PSO算法

PSO(particle swarm optimization)算法名為粒子群優化算法，是早期模擬動物集群行為的一種算法模型，其以迭代的方式來獲得最優解。該算法首先初始化一群隨機產生的粒子，而后在給定的搜索空間中不斷對其自身進行迭代，從而獲得最優的粒子位置和速度，當迭代達到設定的最大循環數和最小適應度閾值后，算法運算終止[17]。

計算中為了確定是否要對找到的最優個體的粒子種群極值和個體極值進行判定更新，需引入適應度函數來進行判斷。適應度函數是由集中計算訓練產生的誤差的平方和來定義的，然后根據所設定粒子的飛行度來產生新個體，當適應度函數值小于10-6時，算法迭代終止。適應度函數如式(1)所示：

(1)

式中：A為模型的訓練值，Ai為模型樣本值。

為了增加PSO算法的收斂性，將慣性權重因子引入到進化方程中，粒子原有的速度保留程度可通過慣性權重來表示。當將原始慣性權重設為0.9時，最終慣性權重將被設定為0.1，此時在算法迭代初期有較高的全局搜索性，并且算法在迭代后期可更精確地對局部進行分析[17]。PSO算法流程如圖1所示。

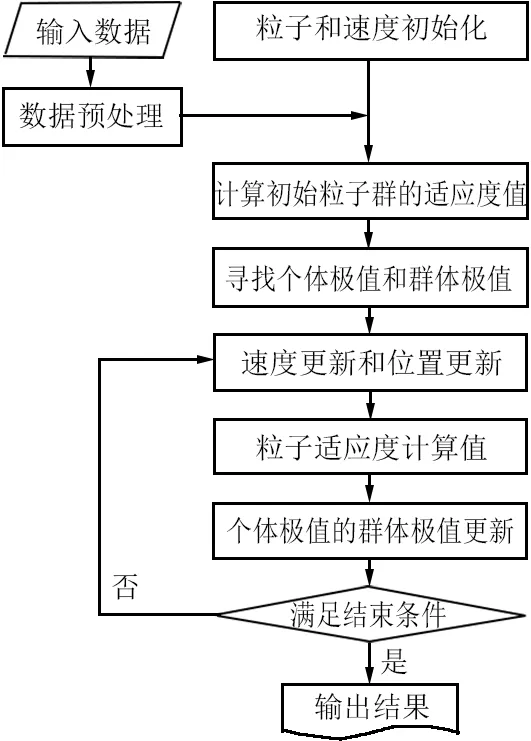
圖1 PSO算法流程圖Fig. 1 Flow chart of PSO algorithm

1.2 試驗條件

試驗在MK2710內外圓數控磨床上進行，機床各軸的最高運動分辨率為1 μm。軸承套圈試件為粗磨溝道后的H7009C氣壓燒結氮化硅陶瓷軸承外圈。砂輪采用RVD人造金剛石圓弧砂輪，砂輪外徑為50 mm，厚度為7.5 mm，端面圓弧半徑為3.75 mm，內孔直徑為10 mm，粒度代號為230/270，濃度為100%。

試驗采用逆磨的磨削方式(工件旋轉方向與砂輪旋轉方向相反)在濕磨下進行，主軸軸向振蕩速度為50 mm/min，通過調整工藝參數(砂輪線速度vs、徑向進給量f、工件轉速vw)來獲得工件加工后不同的表面粗糙度與圓度。用Taylor Hobson S3C輪廓度儀檢測磨削后套圈的表面粗糙度，用Taylor Hobson TR 385圓柱度儀測量溝道圓度，采樣點數為18 000個。為了確保數據準確，表面粗糙度Ra與圓度R0均為多點測量后的平均值。

加工試驗時不同工藝參數下的粗糙度和圓度值如表1所示，通過表1的試驗數據進行工藝參數與表面粗糙度和溝道圓度的數值擬合(一元模型)。

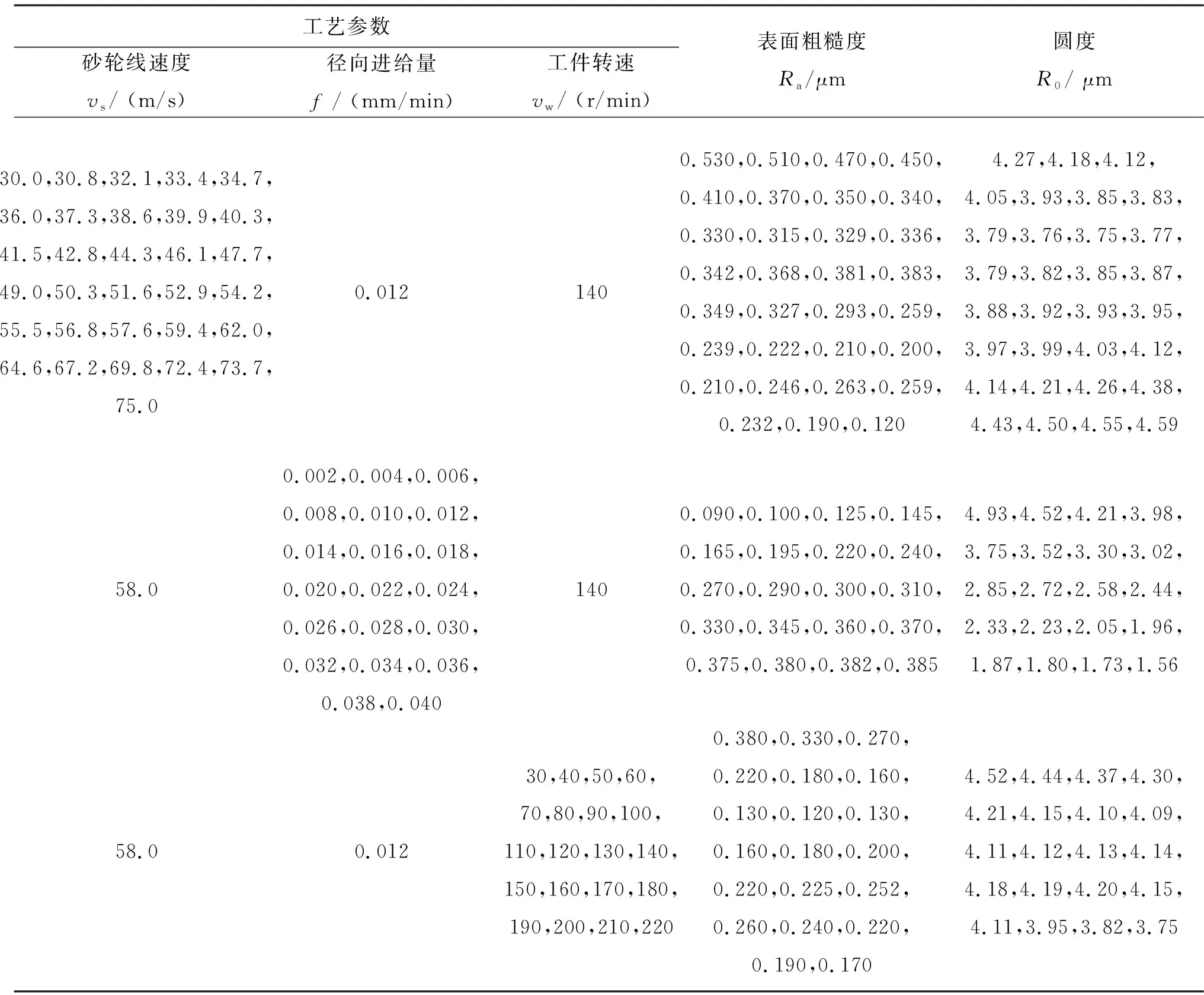
表1 不同工藝參數下的粗糙度與圓度(一元模型數值擬合)Tab. 1 Roughness and roundness under different process parameters (numerical fitting of unitary model)

2 表面粗糙度模型的擬合與檢驗

2.1 工藝參數與表面粗糙度數值擬合

2.1.1 砂輪線速度與表面粗糙度

氮化硅陶瓷軸承套圈磨削時砂輪線速度與表面粗糙度關系曲線如圖2所示。當徑向進給量f=0.012 mm/min，工件轉速vw=140 r/min，砂輪線速度vs由30.0 m/s增加到75.0 m/s時，表面粗糙度值Ra先由0.530 μm減小到0.315 μm，后增加到0.383 μm，而后又降低到0.200 μm，在此基礎上又繼續增加到0.263 μm，最后降低到0.120 μm。出現此現象的原因是砂輪線速度增加導致了磨削區溫度升高，溫度的升高在一定程度上會使陶瓷表面產生玻璃相而軟化，增大材料的斷裂韌性，使得表面更多以塑性變形的方式去除，表面質量變好[2-5]，致使表面粗糙度整體呈減小的趨勢。

根據圖2中散點的分布，判斷表面粗糙度模型為截斷的正弦函數模型，由于數值增值差距較大，因此在正弦函數前乘上二次項bvs2+cvs+d加以修正，據此建立的表面粗糙度關于砂輪線速度的一元模型如式(2)所示：

Ra1=a(bvs2+cvs+d)sin(gvs+h)+k

(2)

通過最小二乘法進行擬合，求解得一元模型如式(3)所示：

Ra1=1.26(-0.0027vs2+0.0626vs-1.256)×sin(0.1222vs-0.168)+0.5125

(3)

在模型中隨機代入試驗點進行驗證，擬合曲線如圖2所示。計算得出其模型預測值與試驗值相關系數為0.969 2，表明該模型具有較高精度。

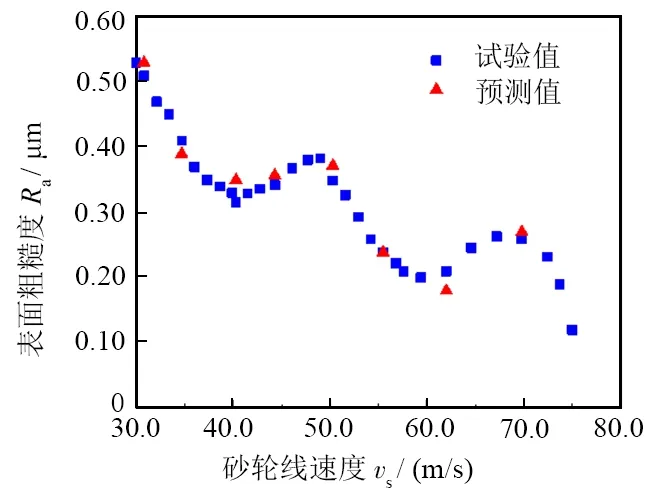
圖2 砂輪線速度與表面粗糙度關系Fig. 2 Relationship between grinding wheel speed and surface roughness

2.1.2 徑向進給量與表面粗糙度

氮化硅陶瓷軸承套圈磨削時徑向進給量與表面粗糙度關系曲線如圖3所示。

當砂輪線速度vs=58.0 m/s、工件轉速vw=140 r/min，徑向進給量f由0.002 mm/min增加到0.040 mm/min時，表面粗糙度值Ra由0.090 μm增加到0.385 μm，且上升趨勢逐漸變緩。原因是徑向進給量增加，砂輪與工件的接觸弧長增加，去除量增大，磨削抗力變大，導致材料的去除方式向脆性斷裂轉變，因此表面粗糙度呈增大趨勢。

根據圖3中散點的分布，判斷其Ra模型為以歐拉系數e為底的指數函數。通過最小二乘法擬合求得表面粗糙度對徑向進給量的一元模型如式(4)所示：

Ra2= -0.396e-0.1502f+0.434

(4)

在模型中隨機代入試驗點進行驗證，該模型擬合曲線如圖3所示。計算得出其相關系數為0.979 8，表明該模型具有較高精度。

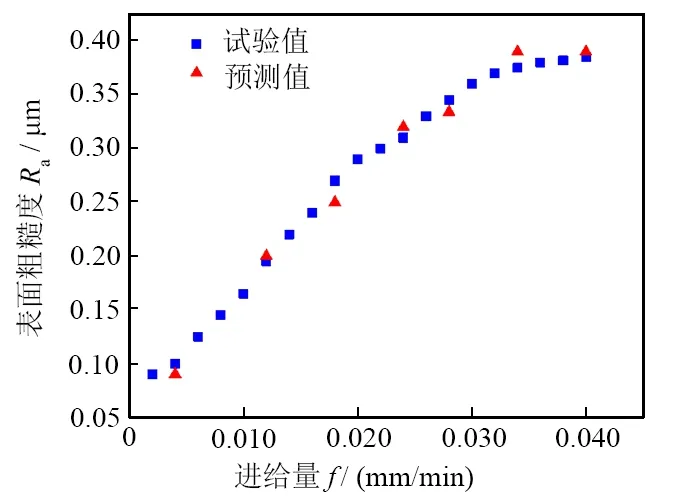
圖3 徑向進給量與表面粗糙度關系Fig. 3 Relationship between feed rate and surface roughness

2.1.3 工件轉速與表面粗糙度

氮化硅陶瓷軸承套圈磨削時工件轉速與表面粗糙度關系曲線如圖4所示。當砂輪線速度vs=58.0 m/s、徑向進給量f=0.012 mm/min，工件轉速vw由30 r/min增加到220 r/min時，表面粗糙度值Ra先由0.380 μm下降到0.120 μm，后又增加到0.260 μm，最后減小到0.170 μm。這是因為隨著工件轉速增加，在磨削力與砂輪工件接觸時間的共同作用下，磨削接觸區積累的熱量較多，陶瓷材料塑性去除所占的比例較大，磨削后的表面質量較好，因此表面粗糙度先呈減小趨勢。而隨著工件轉速的繼續增加，單位面積上參與磨削的有效磨粒數增多，進而磨粒的最大切削厚度變大，使得陶瓷表面更多以脆性斷裂的方式去除，表面質量變差，因此粗糙度又呈增大趨勢[2]。當轉速增大到一定程度后，因為高溫的作用，材料的斷裂韌性增加，塑性去除比例大于脆性去除比例，因此粗糙度值又減小。

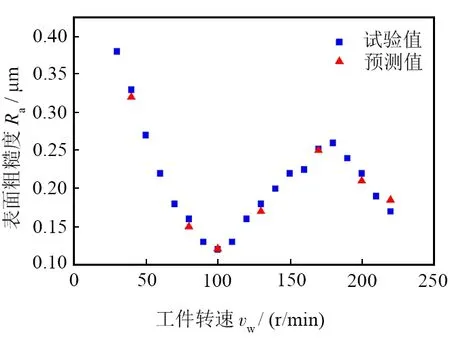
圖4 工件轉速與表面粗糙度關系Fig. 4 Relationship between workpiece rotation speed and surface roughness

根據圖4中散點分布，判斷Ra模型為截斷的正弦函數模型，由于數值的幅值有下降的趨勢，因此在正弦函數前乘上冪函數加以修正。通過最小二乘法擬合求得表面粗糙度關于工件轉速的一元模型如式(5)所示：

Ra3=0.156vw-0.213sin(0.121vw+0.982)+0.2252

(5)

在模型中隨機代入試驗點進行驗證，該模型擬合曲線如圖4所示。計算得出其相關系數為0.976 9，表明該模型具有較高精度。

2.2 粗糙度多元模型的建立與檢驗

2.2.1 模型建立

根據式(3)～式(5)的單因素數值擬合結果，將式(3)～式(5)相加后整合建立氮化硅陶瓷外圈磨削粗糙度關于工藝參數的多元模型，如式(6)所示：

Ra(vs,f,vw) =n1×vwn2×(n3vs2+n4vs+

n5)×sin(n6vsvw+n7)+n8en9 f+n10+n11

(6)

式中：n1～n11為試驗常數，由試驗中氮化硅陶瓷和金剛石砂輪的材料屬性共同決定。

為了求解式(6)中的相關系數，額外設計表2的系數求解試驗，表2中A、B、C分別代表vs、f、vw。

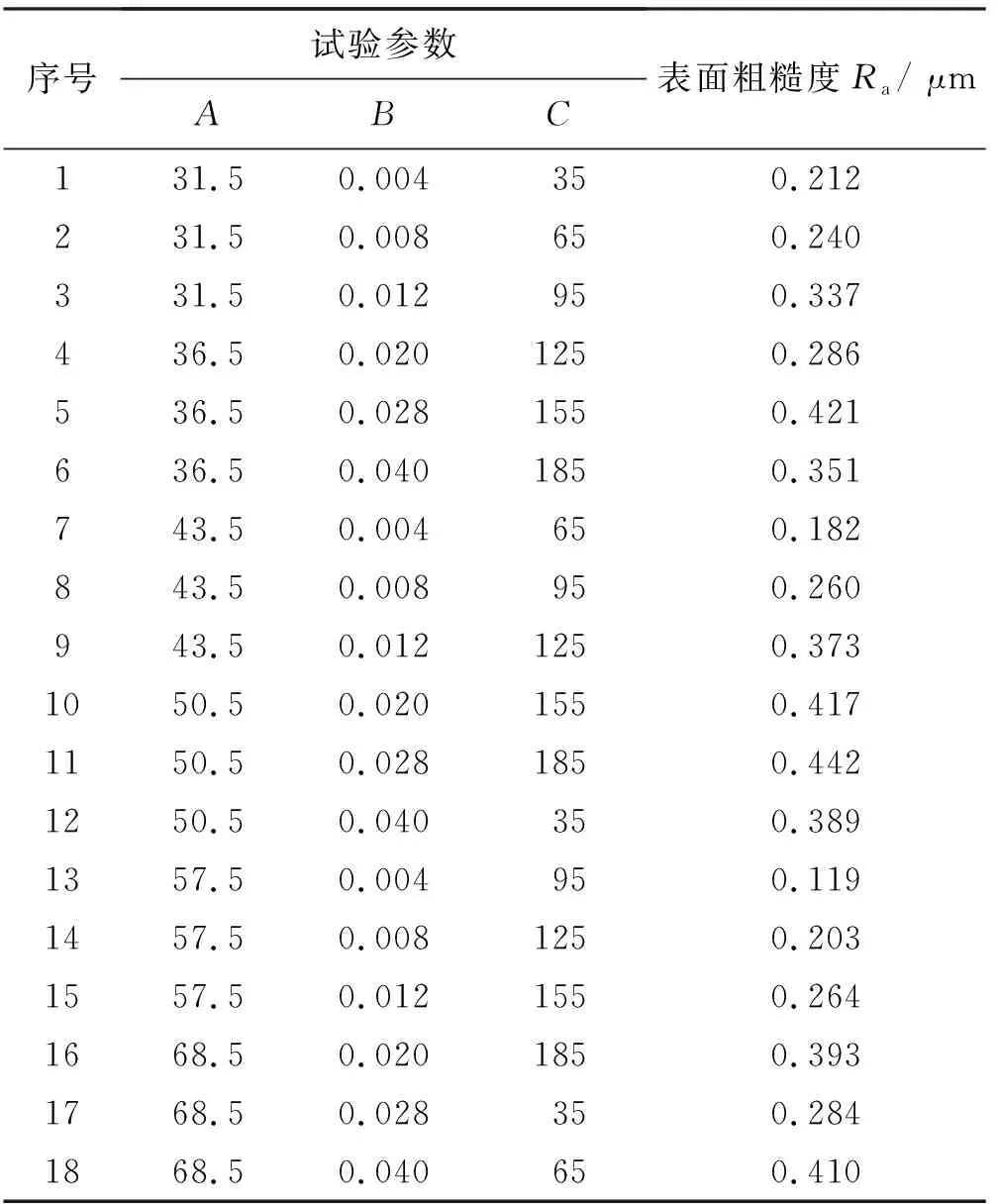
表2 試驗系數求解—表面粗糙度Tab.2 Solving experimental coefficients-surface roughness

基于表2系數求解試驗的結果，利用PSO算法對多元模型進行系數優化求解，求解過程中以多元模型預測值與表2試驗值的方差最小作為粒子適應度準則，如式(1)所示，式中A為多元模型的預測值，Ai為正交試驗值。使用PSO算法對多元模型進行求解，最終得到氮化硅陶瓷軸承外圓磨削表面粗糙度關于工藝參數的多元模型如式(7)所示。

Ra(vs,f,vw) =1.96vw-0.042×(0.0023vs2+0.362vs+12.25)×sin(2.454vsvw+11.73)+e-0.4621f+1.065+0.208

(7)

2.2.2 模型驗證

為了驗證多元模型的精度，再次設計如表3所示的模型驗證試驗，D與E分別表示粗糙度的試驗值和預測值，模型的預測值與試驗值的對比如圖5所示。

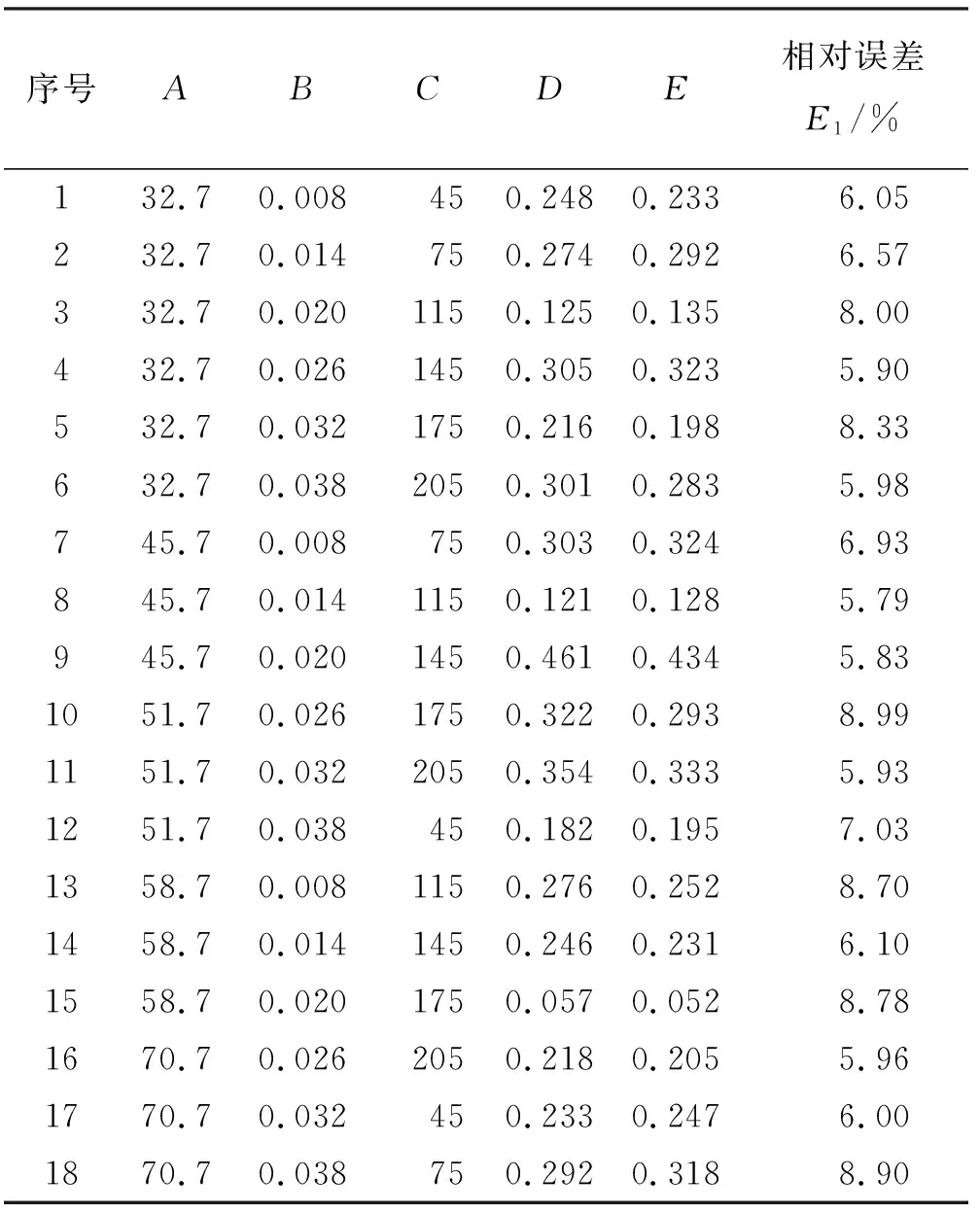
表3 精度驗證試驗—表面粗糙度Tab. 3 Accuracy verification experiment-surface roughness

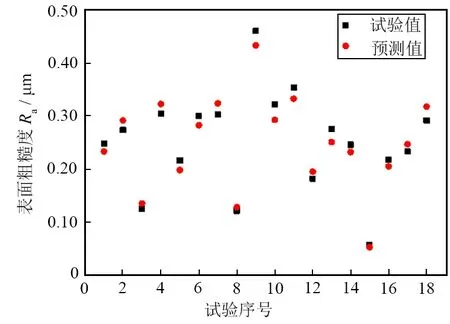
圖5 粗糙度模型的預測值與試驗值對比Fig. 5 Comparison of predicted value and experimental value of roughness model

經計算，試驗值與預測值的相對誤差(表3中E1為絕對值)在5.83%～8.99%，在合理的范圍內，表明該多元模型可以很好地反映實際加工情況，具有一定的可信度。

3 溝道圓度模型的擬合與檢驗

3.1 工藝參數與圓度數值擬合

3.1.1 砂輪線速度與圓度

氮化硅陶瓷軸承套圈磨削時砂輪線速度與溝道圓度關系曲線如圖6所示。當徑向進給量f=0.012 mm/min、工件轉速vw=140 r/min，砂輪線速度vs由30.0 m/s增加到75.0 m/s時，溝道圓度值Ro先由4.27 μm減小到3.77 μm，隨后又增加到4.59 μm，且增加趨勢明顯。出現此現象的原因是砂輪線速度的增加會使單顆磨粒的最大切削厚度減小，使表面更多以塑性變形的方式去除，并不會在磨削接觸區域出現表面剝落等現象，因此溝道圓度先減小。而隨著砂輪線速度的繼續增大，主軸的轉速也隨之增大，會引起機床主軸的振動，進而影響溝道圓度，因此會呈現先減小后增大的趨勢。

根據圖6中散點的分布，判斷Ro模型為截斷的正弦函數模型，由于數值的幅值不對稱，因此在正弦函數前乘上一次項vs加以修正，據此建立的溝道圓度關于砂輪線速度的一元模型為Ro1=avssin(bvs+c)+d。通過最小二乘法進行擬合，求解得一元模型如式(8)所示：

Ro1=-0.077vssin(16.62vs-27.24)+0.417

(8)

在模型中隨機代入試驗點進行驗證，該模型擬合曲線如圖6所示。計算得到其相關系數為0.952 1，表明該模型具有較高精度。

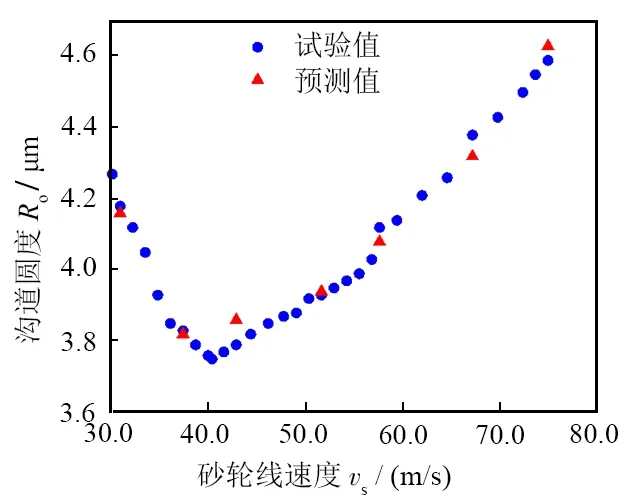
圖6 砂輪線速度與溝道圓度關系Fig. 6 Relationship between grinding wheel speed and raceway roundness

3.1.2 徑向進給量與圓度

氮化硅陶瓷軸承套圈磨削時徑向進給量與溝道圓度關系曲線如圖7所示。當砂輪線速度vs=58.0 m/s，工件轉速vw=140 r/min，徑向進給量f由0.002 mm/min增加到0.040 mm/min時，溝道圓度值Ro由4.93 μm減小到1.56 μm，且下降趨勢先急后緩。這是因為徑向進給量增加，磨削接觸弧長增大，砂輪與工件作用路徑增長，磨削區的熱流密度增加[18]，材料的斷裂韌性隨之增加，材料表面以塑性變形的方式去除，磨削力較小，因此溝道圓度呈減小趨勢。

根據圖7中散點的分布，判斷Ro模型為以歐拉系數e為底的指數函數。通過最小二乘法擬合求得溝道圓度關于徑向進給量的一元模型，如式(9)所示：

Ro2= -0.968e0.0774f+6.031

(9)

在模型中隨機代入試驗點進行驗證，該模型擬合曲線如圖7所示。計算得到其相關系數為0.923 3，表明該模型具有較高精度。

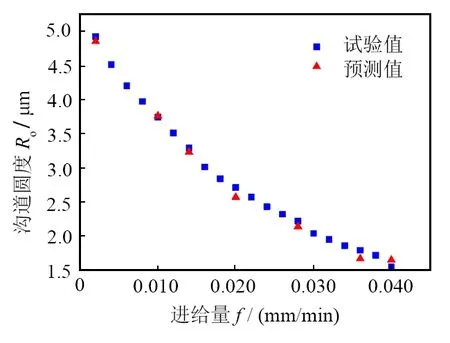
圖7 徑向進給量與溝道圓度關系Fig. 7 Relationship between feed rate and raceway roundness

3.1.3 工件轉速與圓度

氮化硅陶瓷軸承套圈磨削時工件轉速與表面粗糙度關系曲線如圖8所示。當砂輪線速度vs=58.0 m/s，徑向進給量f=0.012 mm/min，工件轉速vw由30 r/min增加到220 r/min時，溝道圓度值Ro先由4.52 μm下降到4.09 μm，后又增加到4.20 μm，最后減小到3.75 μm。出現此現象的原因是工件轉速增加，砂輪上磨粒的實際切削厚度減小，降低了每個磨粒的切削力，所以整體磨削力降低[19]，溝道圓度總體呈減小趨勢。在110～170 r/min出現回升趨勢是由于工件轉速增大，單位面積上參與磨削的有效磨粒數增加，并且金剛石砂輪的導熱性要優于陶瓷的，在較短的熱源作用時間下大部分熱被傳入砂輪中[4]，使材料表面脆性剝落少量增加，因此溝道圓度有小幅度增高。

根據圖8中散點分布，判斷Ro模型為二次函數，由于數值的不對稱性，因此在二次函數前乘上以歐拉系數e為底的指數函數加以修正。通過最小二乘法擬合求得溝道圓度關于工件轉速的一元模型，如式(10)所示：

Ro2= 0.032e2.56vw(-11.63vw2+128.31vw-23.28)+3.936

(10)

在模型中隨機代入試驗點進行驗證，該模型擬合曲線如圖8所示。計算得出其相關系數為0.962 2，表明該模型具有較高精度。

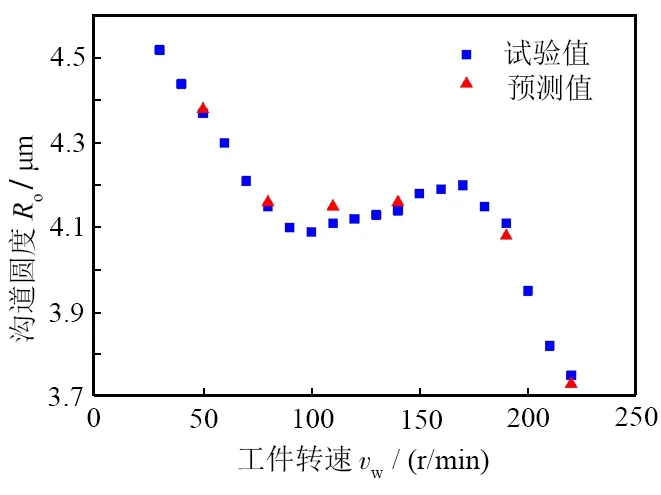
圖8 工件轉速與溝道圓度關系Fig. 8 Relationship between workpiece rotation speed and raceway roundness

3.2 圓度多元模型的建立與檢驗

3.2.1 模型建立

根據式(8)～式(10)的單因素數值擬合結果，整合建立氮化硅陶瓷外圈磨削圓度對工藝參數的多元模型，如式(11)所示：

Ro(vs,f,vw) =m1×vssin(m2vs+m3)×(m4vw2+m5vw+m6)+m7em8 f+m9vw+m10

(11)

式中：m1～m10為試驗常數，由試驗中氮化硅陶瓷和金剛石砂輪的材料屬性共同決定。

為了求解式(11)中的相關系數，采用與表2中相同的試驗參數對式(11)的系數進行求解，試驗結果如表4所示。

同樣在系數求解試驗結果的基礎上利用PSO算法進行優化求解，采用式(1)的適應度函數，最終得到氮化硅陶瓷軸承外圓磨削溝道圓度關于工藝參數的多元模型如式(12)所示：

Ro(vs,f,vw) =-0.145vssin(2.08vs-72.19) ×

(-35.66vw2+9.83vw-56.75)+0.022e0.172f+1.35vw+3.054

(12)表4 試驗系數求解—圓度Tab. 4 Solving experimental coefficients-roundness

3.2.2 模型驗證

為了驗證多元模型的精度，采用表5所示的模型驗證試驗對模型精度進行驗證，表中F、G分別表示圓度的試驗值與預測值。模型的預測值與試驗值的對比如圖9所示，計算得到試驗值與預測值的相對誤差(表5中E2為絕對值)在4.62%～8.01%，在合理的范圍內，表明該多元模型可以很好地反映實際加工情況，具有一定的可信度。

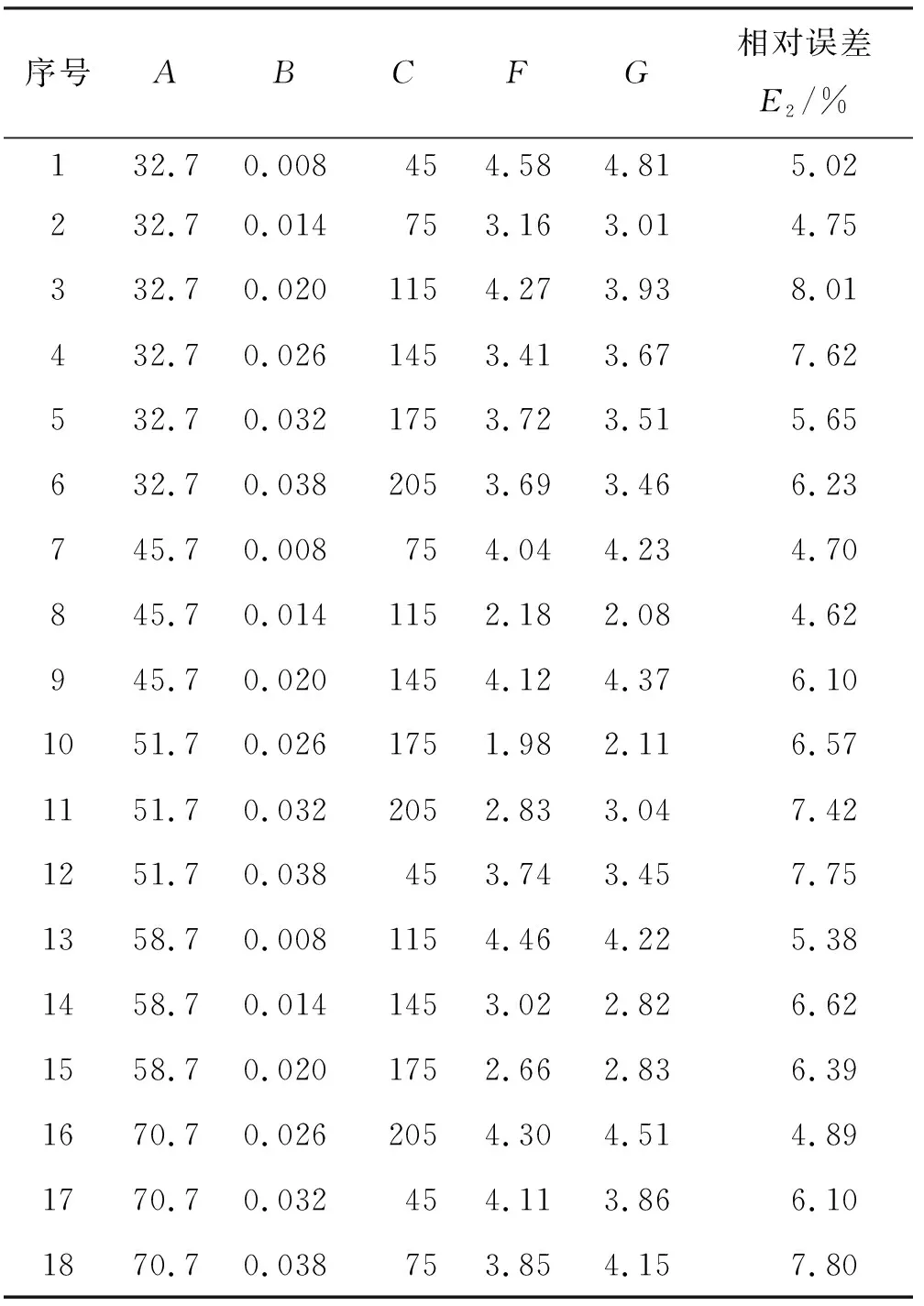
表5 精度驗證試驗-圓度Tab. 5 Accuracy verification experiment-roundness

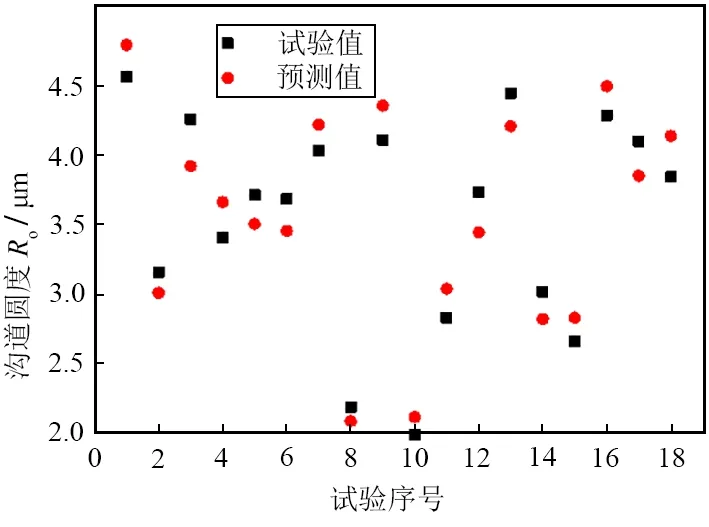
圖9 圓度模型預測值與試驗值對比Fig. 9 Comparison of predicted value and experimental value of roundness model

4 基于PSO算法的雙目標優化與檢驗

4.1 雙目標優化

在日常磨削加工中，工藝參數對陶瓷軸承外圓磨削的加工質量影響較為復雜，在保證粗糙度值小的同時還要保證圓度值小，因此結合實際加工情況，建立基于表面粗糙度和溝道圓度模型的雙目標優化模型，如式(13)所示：

(13)

式中：H1和H2為Ra和Ro的雙目標函數，vs、f、vw3個參數的選取范圍為約束條件。

為了使表面粗糙度和溝道圓度對優化結果的影響權重接近一致，在圓度Ro前乘以常數系數0.1，得到算法的適應度函數如式(14)所示。通過PSO算法對雙目標模型進行優化求解，得到優化后加工工藝參數為vs=56.0 m/s、f=0.012 mm/min、vw=215 r/min，此時加工后對應的表面粗糙度值為0.130 μm，圓度值為2.20 μm。

Fit′=Ra+0.1×Ro

(14)

4.2 優化結果檢驗

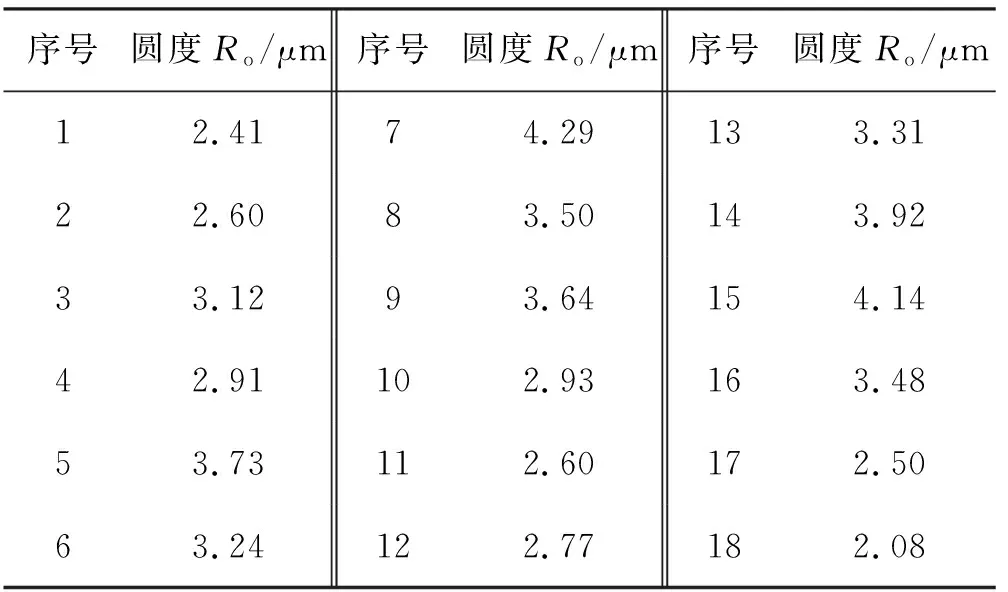
將雙目標優化后的工藝參數應用于實際加工中，另外再額外進行與之不同的9組參數進行對比，結果如表6所示。其中，序號1為優化后參數，其余為隨機參數。從表6中可看出：優化后的工藝參數能同時保證粗糙度值和圓度值相對較小，達到最優工藝參數條件。

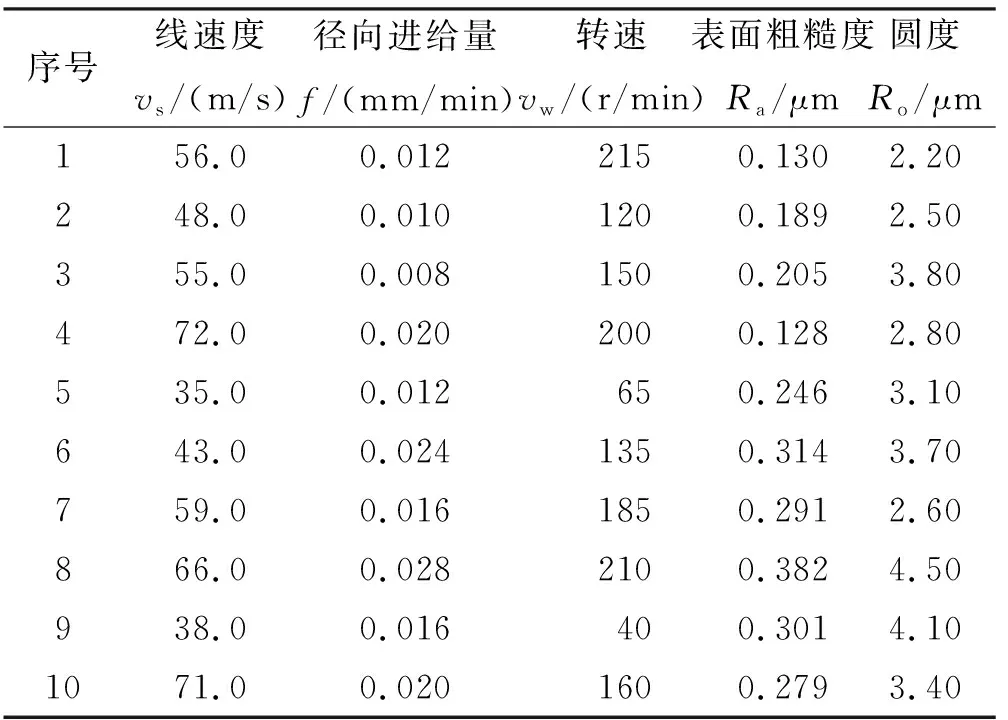
表6 工藝參數結果對比Tab. 6 Comparison of process parameter results

5 結論

在單因素試驗下分別研究了工藝參數對氮化硅軸承套圈表面粗糙度和溝道圓度的影響規律，基于試驗值和PSO算法，利用最小二乘法建立了粗糙度和圓度的多元模型，并對其進行了驗證，主要結論如下：

(1) 基于砂輪線速度、徑向進給量和工件轉速對粗糙度的一元模型建立了表面粗糙度對工藝參數的多元復合模型，該模型預測值和實際加工值的相對誤差在5.83%～8.99%，表明多元模型可較為準確地預測實際加工時Ra情況。

(2) 基于砂輪線速度、徑向進給量和工件轉速對圓度的一元模型建立了溝道圓度對工藝參數的多元復合模型，該模型預測值和實際加工值的相對誤差在4.62%～8.01%，表明多元模型可較為準確地預測實際加工時Ro情況。

(3) 通過對氮化硅陶瓷外圓磨削的粗糙度和圓度的雙目標函數進行優化，得到優化后工藝參數為vs=56.0 m/s、f=0.012 mm/min、vw=215 r/min，此時的粗糙度與圓度分別為0.130 μm和2.20 μm，且此參數加工后可同時得到較小的粗糙度值與圓度值。