基于振動臺試驗的黃土場地具有地上結構地鐵車站地震反應特性分析

韓建平 張虎虎

（1.蘭州理工大學甘肅省土木工程防災減災重點實驗室，蘭州730050；2.蘭州理工大學西部土木工程防災減災教育部工程研究中心，蘭州730050）

0 引 言

近年來，隨著城市規模的快速發展及其交通需求的不斷增大，我國西部黃土地區地鐵工程建設發展迅速。截至2020年，西安市已開通地鐵線路5條，總里程達161.5 km，在建線路11條，遠景規劃總里程達420 km；蘭州市已開通地鐵線路1條，總里程達26 km，在建線路1條，里程為9.4 km。由于黃土具有大孔隙和弱膠結等結構特性，因此其表現出極高的地震易損性［1］。而地鐵車站作為生命線工程，在緊急狀況下，人流疏散困難，在地震下車站結構一旦發生倒塌破壞，所造成的人員傷亡將是十分慘重的，并且地鐵車站埋置于地下，震后修復難度大，代價高。但目前針對黃土這種特殊地質條件下地下結構抗震性能的研究成果相對較少［2-5］。因此開展黃土場地中地鐵車站結構的地震反應特性研究迫在眉睫。

自1995年日本阪神地震中大開地鐵車站遭受嚴重破壞后，國內外學者對地下結構地震反應特性及破壞機理和失效模式開展了廣泛而深入的研究，已形成了較為深刻的認識［6-8］。地下結構地震反應主要受控于周圍地基土的動力特性［9-12］；地下結構的破壞機理和失效模式是在強烈水平地震動作用下，周圍土體發生過大剪切變形致使車站結構產生過大的層間位移，而車站結構中柱抗剪強度和變形能力不足，最終發生剪切破壞和彎曲破壞［13-16］。然而，目前針對具有地上結構的地鐵車站地震反應特性的研究幾乎空白。

因此，本文以蘭州黃土場地中某具有兩層地上結構的地鐵車站為原型，基于縮尺模型的振動臺試驗數據，分析模型體系各階段的基頻、加速度和水平位移反應以及模型車站的應變和側墻處的動土壓力反應，目的是探索黃土場地條件下具有地上結構的地鐵車站地震反應規律，揭示其地震損傷和災變機制。

1 振動臺試驗概況

本次試驗采用蘭州地鐵某站臺施工基坑的黃土為模型地基土，在蘭州理工大學地震模擬振動臺上進行了幾何比例為1∶30的具有兩層地上結構的地鐵車站模型試驗。模型土箱采用疊層剪切土箱，內部凈尺寸為2.95 m×1.95 m×1.9 m。模型車站采用由微粒混凝土澆筑的地下一層、地上兩層的三層三跨矩形斷面結構。模型試驗的傳感器布置如圖1所示，試驗方案詳見文獻［5］。

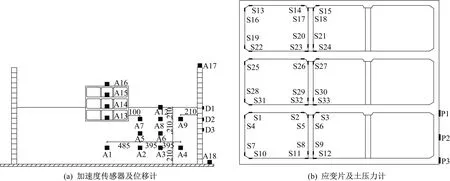
圖1 振動臺試驗傳感器布設Fig.1 Arrangement plan of sensors for shaking table test

振動臺試驗加載工況如表1所示。

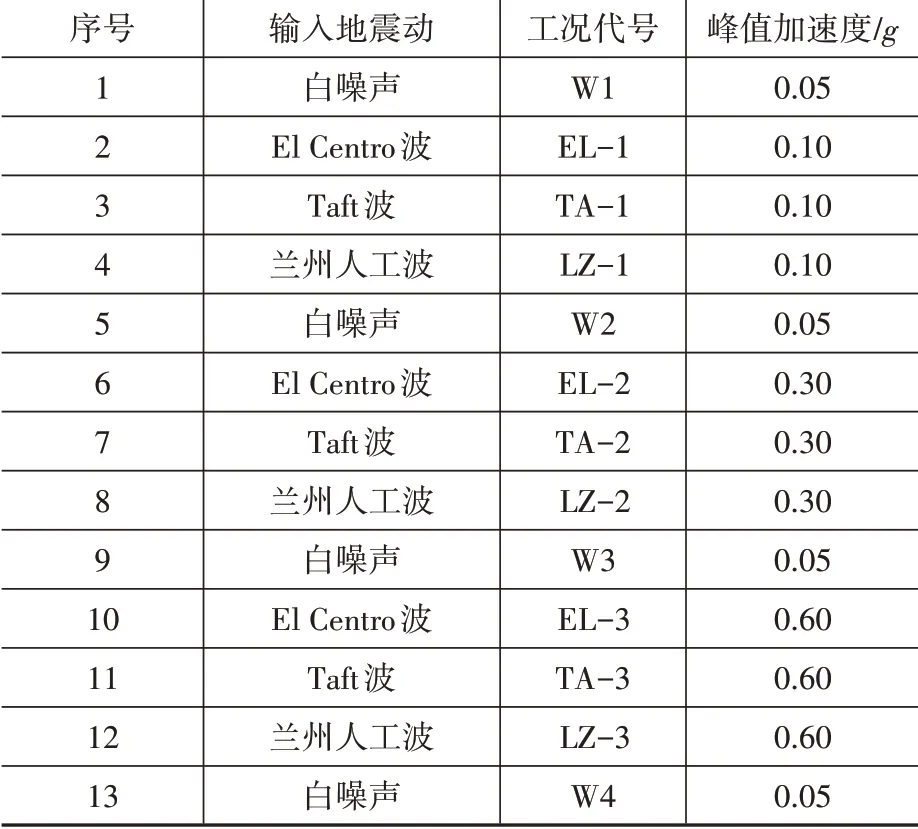
表1 振動臺試驗加載工況Table 1 Loading cases for shaking table test

2 試驗結果與分析

2.1 模型體系基頻

計算模型地基土中A8、A12測點，地下結構A13、A14測點及地上結構A16測點相對于模型土箱底部A18測點的互相關函數，利用時域ITD法，識別各次白噪聲工況下模型體系的基頻如表2所示。

由表2可知，在前三次白噪聲掃頻下相同深度處的地基土和地下結構基頻基本一致。這一方面說明在較小地震動作用下，地下結構與其一定水平距離處的地基土剛度差異較小，土體密實度未發生明顯變化，地下結構未發生明顯損傷；另一方面表明地基土與地下結構始終緊密接觸協同振動。第四次掃頻時地下結構-土體系基頻驟增。這可能是由于在較大地震動作用下，土-地下結構動力相互作用強烈，以至于兩者之間已產生間隙，當白噪聲掃頻時，土與地下結構瞬時碰撞產生散射和反射效應，致使土與地下結構體系基頻均驟增。四次白噪聲掃頻得到的地上結構基頻不斷降低，說明在振動臺試驗過程中地上結構損傷不斷累積，剛度逐漸降低。

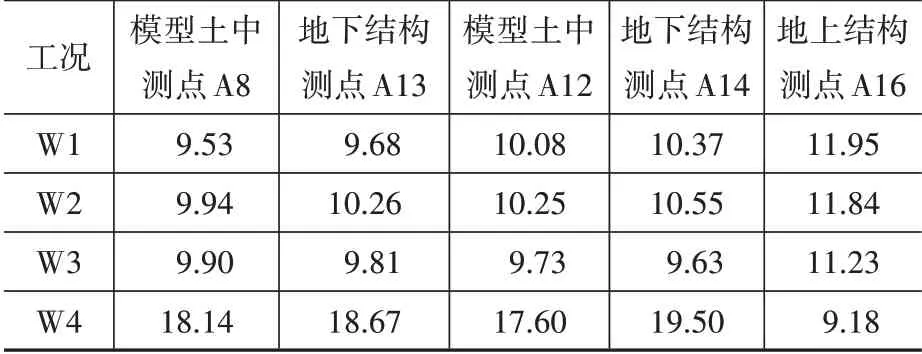
表2 不同測點加速度計獲得的基頻Table 2 Fundamental frequencies calculated by different accelerometers Hz

2.2 模型體系加速度反應

以A3加速度傳感器所測峰值加速度為基準值，利用土體深度方向布設的A6、A8和A12加速度傳感器所測的峰值加速度計算地基土加速度放大系數，如圖2所示。在不同地震動輸入下，地基土加速度放大系數自下而上呈現先減小后增大的規律。這可能是由于地基土分層填筑時，在0.4～0.6 m深度范圍夯實度比其他深度范圍較小所致。從圖2（a）可知，當地震動峰值加速度增大時，深層地基土（0.4～0.6 m深度范圍）的加速度放大系數變化幅度較小，淺層地基土（0～0.2 m深度范圍）的加速度放大系數變化幅度較大，在地表處尤為顯著，且呈現出不斷減小的規律。這進一步表明試驗過程中深層地基土的密實度未發生明顯變化，淺層地基土中由于土-結構相互作用的存在，對地震動能量具有較大的消耗作用，也即表明車站結構的存在對地震動在地基土中的傳播具有一定影響。從圖2（b）和圖2（c）可知，在不同地震動輸入下，淺層地基土中的加速度放大系數為El Centro地震動記錄作用下最大，蘭州人工波作用下次之，Taft地震動記錄作用下最小，在地表處尤為顯著。在深層地基土中，不同地震動輸入下的土層加速度放大系數差異較小。上述結果表明，在淺層地基土中，地基土加速度放大系數對地震動頻譜特性比較敏感；而在深層地基土中，地震動頻譜特性對土層加速度放大系數的影響較小。

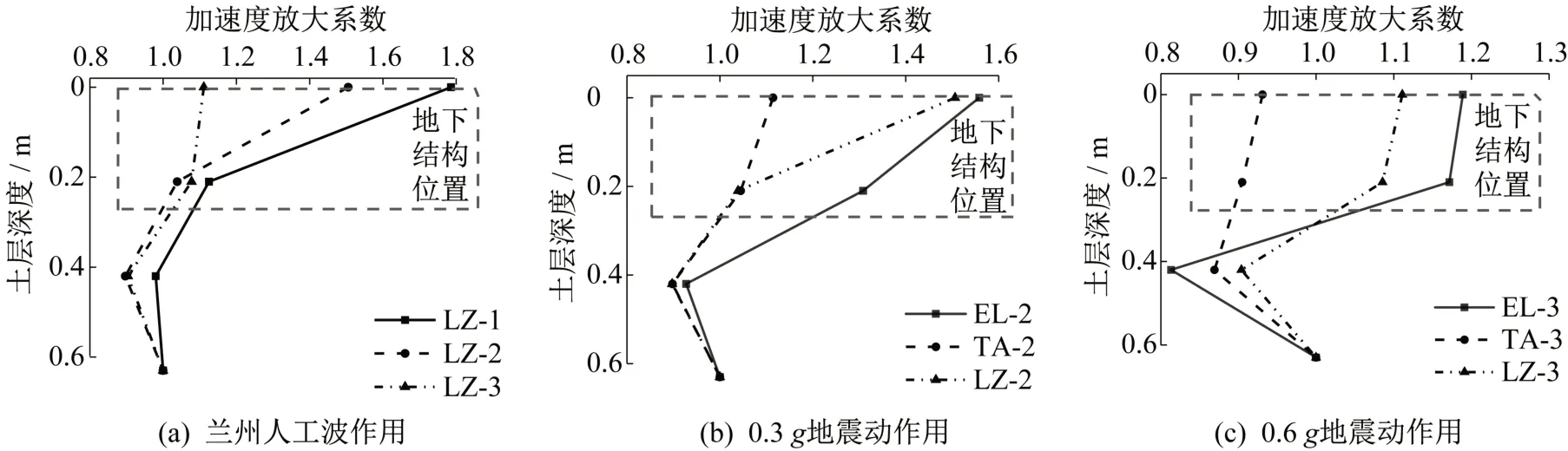
圖2 模型地基土不同深度處的加速度放大系數Fig.2 Acceleration amplification factors at different depths of the model foundation soil

圖3（a）給出了蘭州人工波輸入下車站結構不同高度處的加速度放大系數，可以發現：隨峰值加速度的增加，結構不同高度處的加速度放大系數不斷增大。從圖3（b）和圖3（c）可以看出，在不同地震動輸入下，地上結構同一高度處的加速度放大系數之間無明顯規律。這表明地上結構的加速度反應與地震動特性無明顯關系。同時，不同強度地震動輸入下模型車站結構的加速度放大系數發展規律顯著不同，這是由于振動臺試驗中損傷累積的存在，在0.6g地震動作用下，模型結構已經出現了明顯的非線性反應。對比圖2和圖3中地下結構位置處的地基土加速度放大系數與地下結構上的加速度放大系數，可知地下結構的加速度反應主要受周圍地基土動力反應的影響，故其加速度放大系數對地震頻譜特性有一定的敏感性。

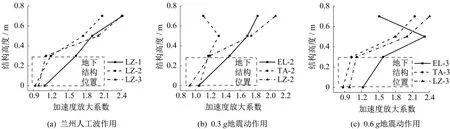
圖3 模型車站結構不同高度處的加速度放大系數Fig.3 Acceleration amplification factors at different heights of the model substation structure

2.3 模型體系水平位移反應

由于振動臺試驗中模型地基土及地下結構的位移反應不易直接測量，故采用將加速度二次積分的方法求得相應位置處的水平位移反應。圖4分別對0.1g和0.6gEl Centro地震動記錄作用下地下結構與同深度地基土的水平位移反應進行了對比，整體而言，同一深度處地基土與地下結構的水平位移大小相等、方向相反，且不同深度處兩者的水平位移分別相等。這一方面表明，地下結構與其一定距離處地基土之間的剛度無明顯差異，且該距離處地基土始終處于彈性狀態；另一方面說明，在土-結構相互作用過程中，地基土與地下結構運動方向相反，地基土對地下結構的變形起到“主動”約束和限制作用，對地下結構抗震具有一定作用。

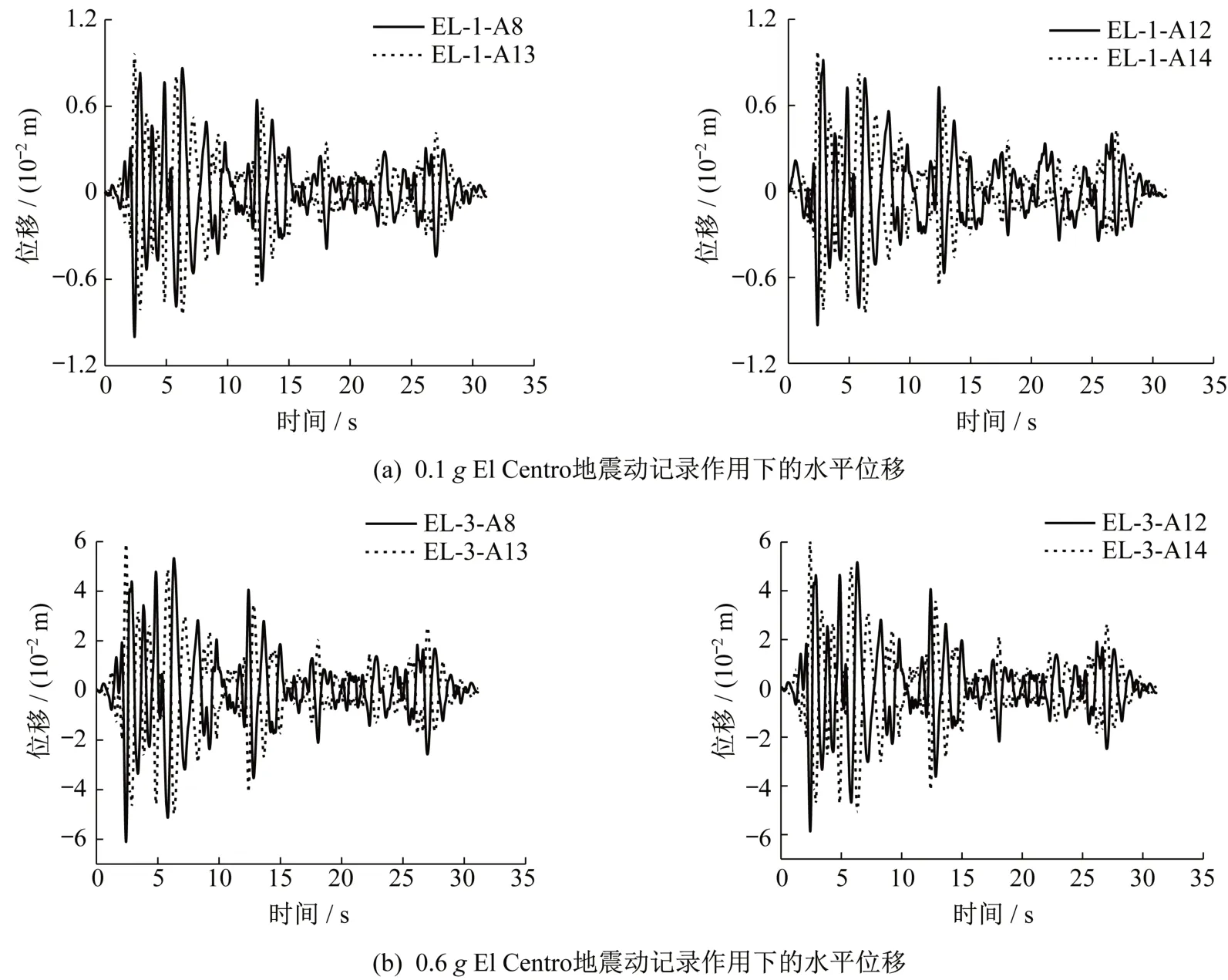
圖4 不同強度地震動作用下模型結構與模型地基的水平位移時程曲線Fig.4 Horizontal displacement time-histories of model structure and foundation under different intensity ground motions

2.4 模型結構動應變反應

不同地震動作用下車站結構不同部位的峰值拉應變分布如圖5所示（注：“0”表示應變計無信號）。

從圖5可以看出：隨地震動峰值加速度的增加，結構各測點處的峰值拉應變逐漸增大。在同一工況下，地下結構的峰值拉應變遠小于地上結構的峰值拉應變，這是由于地下結構受周圍土體的約束作用，在地震動作用下的變形遠小于地上結構。

圖5 不同地震動作用下車站結構峰值拉應變分布圖（單位：10-6）Fig.5 Peak tensile strain in structure under different ground motions（unit：10-6）

模型結構地上第二層中柱柱頂的峰值拉應變始終大于該層中柱柱底的峰值拉應變，地上第一層中柱柱頂的峰值拉應變始終小于該層中柱柱底的峰值拉應變。模型結構地上第二層的頂板截面剛度顯著大于該層底板的，在地震動作用下，當頂板與底板之間發生剪切變形時，中柱頂部與頂板連接處的附加彎矩較大，因此模型結構地上第二層中柱頂部峰值拉應變大于該層中柱底部的。在模型結構地上第一層，一方面，由于底板截面剛度顯著大于頂板的，中柱底部與底板連接處的附加彎矩較大；另一方面，模型結構地上第一層底部位于車站結構地上地下交界處，模型結構在此處剛度突變，在水平地震動作用下，受土-結構動力相互作用和上部結構慣性力耦合作用，承受較大且復雜的剪切和彎曲等作用，極易產生應力集中現象。故模型結構地上第一層中柱柱底的峰值拉應變始終大于該層中柱柱頂的，且是地鐵車站結構的抗震薄弱部位。

在不同強度地震動作用下，除個別工況外，模型結構地上第二層側墻頂部的峰值拉應變始終大于該層側墻底部的。輸入地震動峰值為0.1g和0.3g時，模型結構地上第一層側墻頂部和底部的峰值拉應變差異較小，而當輸入地震動峰值為0.6g時，模型結構地上第一層側墻底部的峰值拉應變顯著大于該層側墻頂部的，表明該層側墻底部發生了嚴重的局部損壞。

在相同強度的地震動作用下，模型結構地上第二層底板靠近中柱處的峰值拉應變始終大于該層底板靠近中柱處的。隨地震動強度的增大，模型結構地上第一層靠近側墻處的峰值拉應變變化并不明顯，而模型結構地上第二層頂板和該層底板靠近側墻處的峰值拉應變均表現為先增大后減小，且底板處的峰值拉應變始終大于頂板處的。這可能是由于在地震動作用下，結構局部區域損傷導致結構剛度不連續，進而影響了結構的整體受力性能。

2.5 動土壓力反應

表3給出了不同地震動作用下模型結構不同高度處的側墻動土壓力增量。可以發現，在峰值加速度為0.1g和0.3g的不同地震動作用下，模型結構側墻動土壓力增量隨埋深增大而增大，側墻底部測點P3動土壓力增量增大效果最為顯著。當輸入地震動峰值為0.6g時，整體而言，側墻頂部測點P1動土壓力增量遠大于側墻中部和底部測點的。

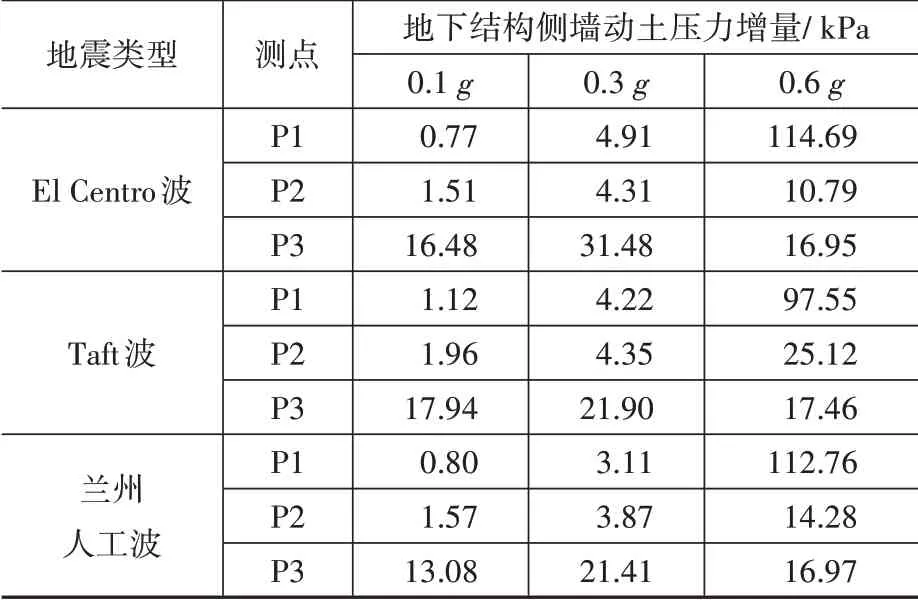
表3 不同地震動作用下地下結構側墻動土壓力增量Table 3 Soil pressure increment at different heights of the model structure under different ground motion

圖6分別繪制了峰值加速度為0.1g和0.6g的蘭州人工波作用下模型結構側墻處測點P1、P2和P3的動土壓力時程曲線。由圖6（a）可知：在0.1g地震動作用下，土體處于彈性變形狀態，且P1和P2測點的初始土壓力大于零，這是因為在振動臺試驗前，通過夯擊制作模型地基時，土和結構緊密接觸，產生一定大小的圍壓；在試驗過程中P1和P2測點動土壓力始終大于零，表明土體與地下結構始終緊密接觸，圍壓效果始終存在。P3測點初始土壓力雖為零，但也始終與地下結構緊密接觸，協同振動。由圖6（b）可知：在0.6g地震動作用下，由于P3測點埋深較大，土-結構相互作用較小，土體仍具有較大的彈性變形性能，能夠與地下結構協同運動，表現為動土壓力時程曲線與坐標橫軸接觸點密集，且橫軸兩側的曲線較為飽滿。P2測點的動土壓力發展大致經歷三個階段。第一階段，土體與地下結構緊密接觸，協同振動，圍壓始終大于零。第二階段，地震動能量不斷累積，土與地下結構不協調振動，發生滑移，地下結構與土體相向運動時，接觸面處的動土壓力增加；而地下結構與土體背向運動時，由于土體彈性變形能力下降，導致接觸面處動土壓力急劇降低，直至為零。第三階段，地震動加載即將結束時，土體與地下結構均復位，兩者的接觸狀態趨于穩定，動土壓力又維持在一定的數值。P1測點的土體在加載前已完全進入塑性狀態，圍壓為零，在地震動加載時，土與結構發生嚴重滑移，地下結構與土體背向運動過程中出現完全脫開現象，且土體始終無法完全復位，因此動土壓力時程曲線表現出瞬降瞬增的單側離散峰值現象。

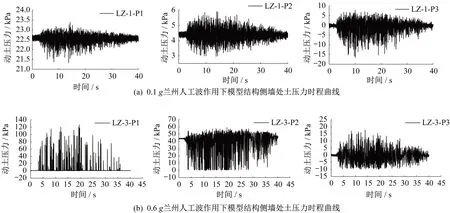
圖6 不同強度地震動作用下側墻動土壓力時程曲線Fig.6 Dynamic soil pressure time-histories of side wall under different ground motions

3 結 論

本文基于黃土場地具有地上結構的地鐵車站考慮土-結構動力相互作用的大型振動臺試驗數據，通過對模型體系基頻、加速度和水平位移反應以及模型車站的應變和側墻處的動土壓力反應的分析，得到以下主要結論：

（1）淺層地基土及埋置于其中的模型車站地下結構的加速度反應對地震動頻譜特性具有較高的敏感性，而深層地基土及模型車站地上結構的加速度反應對地震動頻譜特性敏感性較低。

（2）水平位移反應表明，在土-結構相互作用過程中，地基土與地下結構運動方向相反，地基土對地下結構的變形起到“主動”約束和限制作用。

（3）應變反應表明，由于土體的約束作用，地下結構的應變遠小于地上結構的。模型結構地上第一層中柱底部是地鐵車站結構抗震最薄弱部位，因此在黃土地區具地上結構的地鐵車站抗震設計中應加強此部位的延性，進而提高其抗震性能。

（4）當地震動峰值加速度較小時，模型結構側墻動土壓力增量隨埋深增大而增大；當地震動峰值加速度較大時，不同高度處的土體變形性能差異較大，地表側墻處動土壓力增量遠大于埋深較大側墻處的動土壓力增量。