外貼CFRP加固RC連續梁的抗彎性能及彎矩重分布分析

張智梅 程 雯

（上海大學土木工程系，上海200444）

0 引 言

碳纖維（CFRP）具有高強、耐腐蝕、輕質等突出優點，被廣泛運用于各類鋼筋混凝土受彎構件的加固中［1-5］。對外貼CFRP加固RC梁的探討主要在簡支梁方面［6-7］，然而，在實際工程中需要加固的受彎構件大多為RC連續梁。在結構工程中，RC連續梁的受損破壞在一定程度上會引起整個結構的傾覆。因此近年來國內外學者開始重視對外貼CFRP加固連續梁的研究［8-12］。

分析現有的研究成果可以發現，首先，對外貼CFRP加固連續梁的研究集中在試驗上［10-12］，而關于有限元模擬及理論分析的研究較少；其次，外貼CFRP加固RC連續梁呈現顯著的彎矩重分布，但僅有少量學者討論連續梁的內力重分布［13］；最后，《混凝土結構加固設計規范》（GB 50367—2013）［14］并沒有對外貼CFRP加固RC連續梁的彎矩調幅系數給出明確的數值。若明確外貼CFRP加固RC連續梁的彎矩重分布，便可將按彈性方法計算的彎矩通過彎矩調幅系數進行調整，從而合理地評估結構的承載力，實現設計的優化。

為此，本文首先利用ABAQUS模擬CFRP加固RC連續梁；其次在分析模型上進行影響參數分析，研究各參數對CFRP加固RC連續梁抗彎性能的影響；最后提出連續梁極限破壞時跨中彎矩調幅系數及中支座彎矩調幅系數隨CFRP粘貼長度變化的公式，并利用已有的試驗數據進行驗證，為實際工程設計提供理論依據。

1 非線性有限元數值模擬

1.1 試驗概況

本文選用文獻［15］中的4根連續梁E1至E4建立有限元模型，試驗中E1為未加固梁，E2為負彎矩區加固梁，E3為正彎矩區加固梁，E4為正、負彎矩區同時加固梁。梁的尺寸、加固位置、截面配筋如圖1所示，圖中P代表豎向外加荷載，L1和L2分別表示負、正彎矩區CFRP黏結長度，其中L1和L2長度分別為2 500 mm及3 500 mm，CFRP板厚度為1.2 mm。材料的具體數據如表1所示。

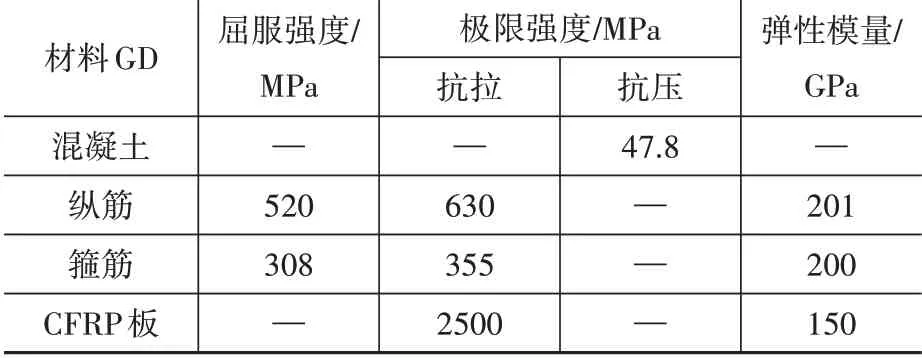
表1 材料的力學性能Table 1 Mechanical properties of materials

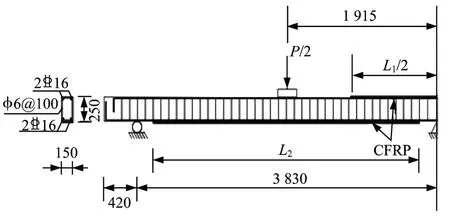
圖1 加固梁簡圖Fig.1 Test piece and reinforcement diagram

1.2 有限元模型的建立

本文應用ABAQUS軟件模擬了連續梁E1至E4。建模時，混凝土的本構用ABAQUS中的塑性損傷模型，其受拉和受壓應力-應變本構分別選取混凝土結構設計規范［16］（以下簡稱規范）中相應的混凝土單軸受拉和受壓本構，并用C3D8R三維實體單元來模擬；鋼筋的本構用規范中有加強段的雙線性彈塑性模型，用T3D2桁架單元來模擬；CFRP板按線彈性材料設置本構，并用C3D8R單元模擬；為了避免產生應力集中現象，在支座處和跨中加載點處分別設置線彈性剛墊塊，其單元類型為C3D8R。

本模型假設鋼筋-混凝土界面和CFRP-混凝土界面之間均不發生黏結滑移，故建模時鋼筋與混凝土采用內置（Embedded）約束；CFRP與混凝土采用綁定（Tie）約束；墊塊與梁的接觸采用綁定（Tie）約束；墊塊與加載點采用耦合（Coupling）約束。根據連續梁實際約束情況，將中支座設置為固結，限定三個方向的位移及轉角，取UR1=U R2=UR3=U1=U2=U3=0；將兩個邊支座設置為鉸結，限定Y軸、Z軸的位移及X軸、Z軸的轉角，取U2=U3=UR1=U R3=0，同時采用位移加載模式進行有限元分析。連續梁E2的模型如圖2所示。

圖2 E2有限元模型Fig.2 Finite element model of E2

1.3 有限元模擬分析與驗證

圖3 為提取模型中的數據得到的荷載-跨中位移曲線與文獻［15］中的相應曲線的對比。表2進一步給出了各試驗梁的關鍵荷載及位移。文獻［15］中未給出試驗屈服荷載及屈服位移，故表2也未給出具體數據。

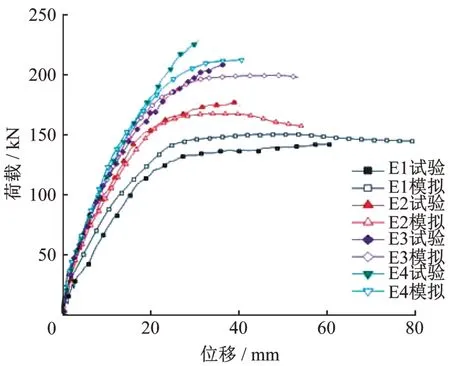
圖3 荷載-跨中位移曲線對比Fig.3 Comparison of load-deflection

由表2可見，CFRP加固連續梁E2、E3、E4與參考連續梁E1相比，位移延性系數減小，模擬的屈服荷載及極限荷載均有提高；模擬的極限荷載值與試驗較接近。

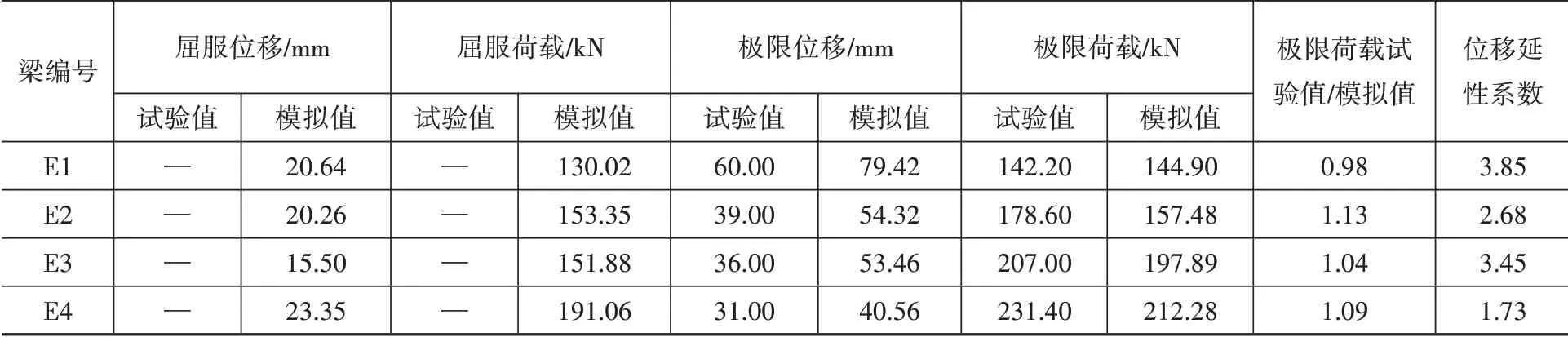
表2 連續梁主要模擬值與試驗結果對比Table 2 Comparison between test results and finite element results

結合圖3及表2可見，梁E1-E4的荷載-跨中位移曲線在鋼筋屈服前與試驗基本吻合，在屈服至極限階段存在一定差異。這些差異出現的原因如下：有限元模擬中的支座約束與真實支座約束存在偏差；模型中混凝土等材料的本構與實際材料的本構有一定差異。綜上，若能確保模擬支座約束與實際一致，材料本構保持一致，則應用ABAQUS軟件對CFRP加固雙跨連續梁進行模擬是切實可行的。

由圖表進一步分析可知，用CFRP加固連續梁能有效地增加梁的抗彎承載力，同時加固連續梁的延性均有一定程度的下降。連續梁的彎矩重分布程度越大則表明塑性鉸轉動能力越強。塑性鉸轉動能力越強表明梁延性越好。若明確CFRP加固鋼筋混凝土連續梁的彎矩重分布，并將其應用于設計中，就可以較為真實地判斷結構的承載能力。因此，在試驗研究有限的情況下，有必要通過已驗證的有限元模型進一步研究CFRP加固鋼筋混凝土連續梁抗彎性能及彎矩重分布特征。

2 加固連續梁抗彎性能的影響參數分析

影響外貼CFRP加固鋼筋混凝土連續梁抗彎性能的主要因素有CFRP加固量、加固位置、黏結長度及CFRP力學性能等。現有研究［5］主要分析了CFRP加固量及其力學性能對加固梁性能的影響，本文擬從改變FRP黏結長度及加固位置的角度，研究其對FRP加固RC連續梁的抗彎性能的影響。

2.1 CFRP黏結長度對負彎矩區加固連續梁的影響

本文以有限元模型E2梁為基礎，保持其他建模參數不變，僅改變CFRP黏結長度，建立了多根負彎矩區加固梁的有限元模型，并定義CFRP黏結長度與梁跨度之比為α1。

表3為不同α1下負彎矩區加固連續梁的主要計算結果及位移延性系數。由表3可得，加固連續梁的屈服荷載隨著α1的增加非線性增加；α1≤0.4時，極限荷載隨著α1的增加而增加，α1＞0.4時，極限荷載基本不變。相比于未加固梁E1，各梁屈服荷載的增幅在9.54%～18.60%之間，極限荷載增幅在6.96%～11.42%之間。同時梁的位移延性系數基本上隨著α1的增大而減小。綜上，當α1=0.4時，負彎矩區加固梁既能獲得較強的承載能力也兼顧了良好的延性。

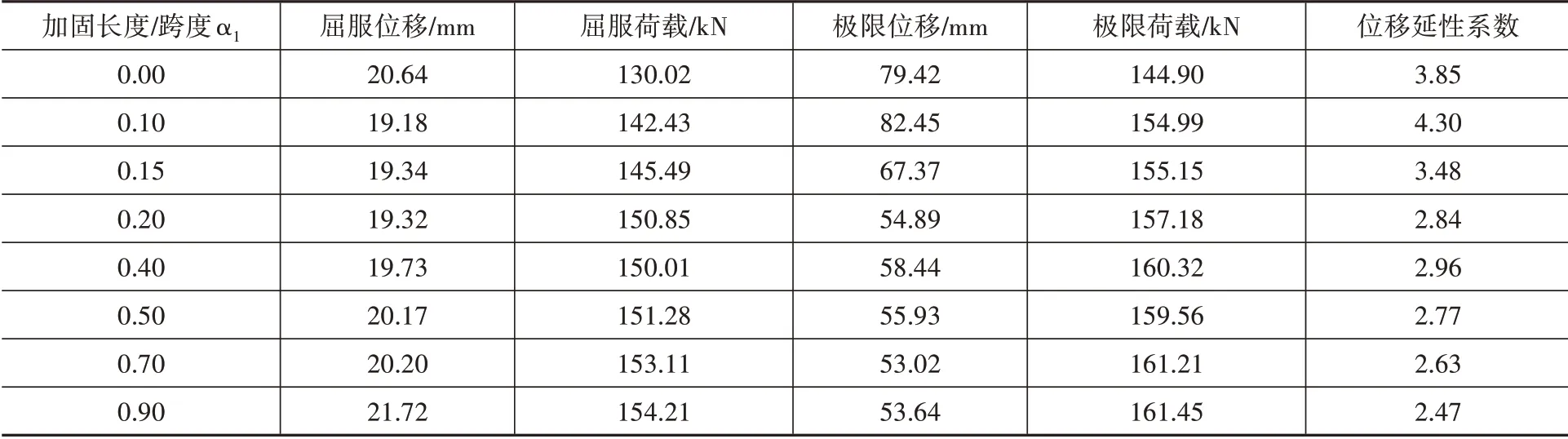
表3 負彎矩區加固主要計算結果Table 3 Main calculation results of beams strengthened in negative moment

2.2 CFRP黏結長度對正彎矩區加固連續梁的影響

本文以有限元模型E3梁為基礎，保持其他建模參數不變，僅改變CFRP黏結長度，建立了多根正彎矩區加固梁的有限元模型，并定義CFRP黏結長度與梁跨度之比為α2，研究α2對加固梁抗彎性能的影響。表4為不同α2下加固連續梁的主要結果及位移延性系數。

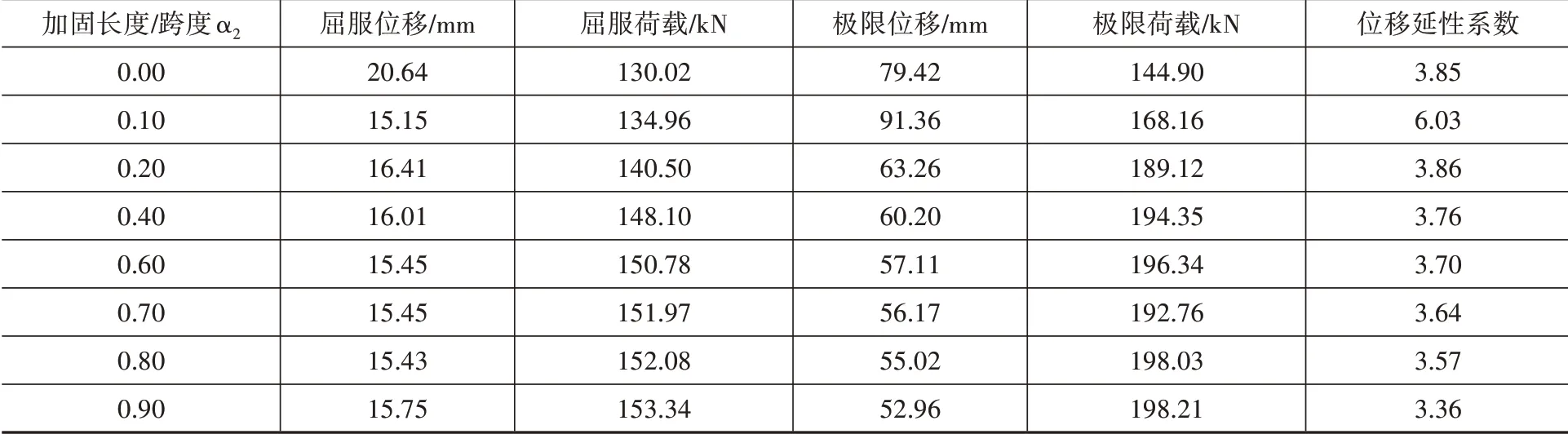
表4 正彎矩區加固主要計算結果Table 4 Main calculation results of beams strengthened in positive moment

由表4可知，從承載力來看，正彎矩區加固連續梁的屈服荷載隨著α2的增加而增加；在α2≤0.6時極限荷載隨著α2的增加而增加，當α2>0.6后極限荷載較為穩定。與未加固梁E1相比，屈服荷載增幅在3.80%～17.94%之間，極限荷載增幅在16.05%～36.79%之間。從變形性能角度上來看，隨著α2的增加，梁達到極限狀態時的位移延性系數一直減小。故可知，正彎矩區加固連續梁的CFRP粘貼長度與梁跨度的最優比值α2為0.6。

3 彎矩重分布研究

連續梁的內力重分布大致分成兩段，第一段是混凝土截面開裂至形成塑性鉸；第二段是塑性鉸形成后到結構處于極限狀態。在這兩個階段中，連續梁的內力重分布集中在第二段。基于以上的理論，本文主要探討第二段的內力重分布。

世界各國研究人員提出許多探究連續梁內力重分布的方法，如塑性鉸法、全過程分析法、變剛度法及彎矩調幅法等。塑性鉸法及變剛度法假定過多；全過程分析法計算過程過于復雜；彎矩調幅法因其思路清晰、計算簡潔而被各國采納。彎矩調幅法是以彈性方法得到的彎矩值按彎矩重分布能力進行適當調整，彎矩重分布能力大小用彎矩調幅系數β來表示，β按下式確定：

式中：MT為有限元分析得到的彎矩值；Me為彈性方法計算的彎矩值。其中梁的實測彎矩由模型提取，彈性彎矩值由力法計算。

表5為在不同α1下負彎矩區加固梁達到極限狀態時的彎矩調幅系數。由表5可知，隨著α1的增加，負彎矩區加固梁的跨中彎矩調幅系數β1及中支座彎矩調幅系數β2均逐漸減小，其中β1降幅在-0.04～-0.17之間，β2降幅在0.07～0.29之間。在α1達到最優值0.4后，β1與β2基本保持不變。

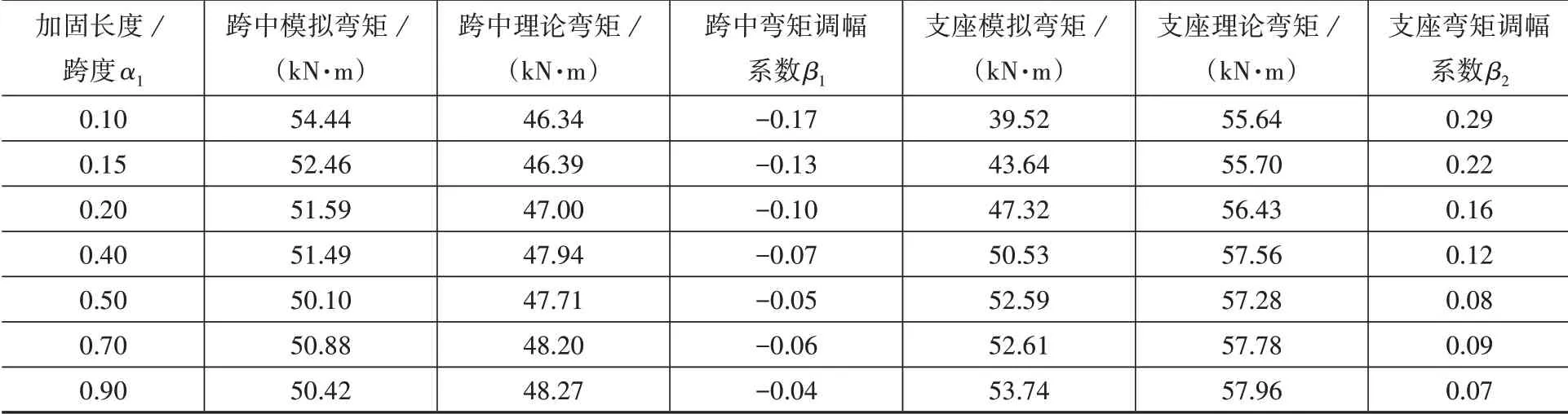
表5 不同α1時極限狀態下關鍵彎矩值Table 5 key bending moment values in limit state under differentα1

基于以上分析，將負彎矩區加固梁的α1～β1及α1～β2的試驗點分成兩段，第一段α1≤0.5，第二段α1>0.5。以α1為橫坐標，以β1，β2為縱坐標，可以得到負彎矩區加固梁的第一段試驗點分布，如圖4所示。

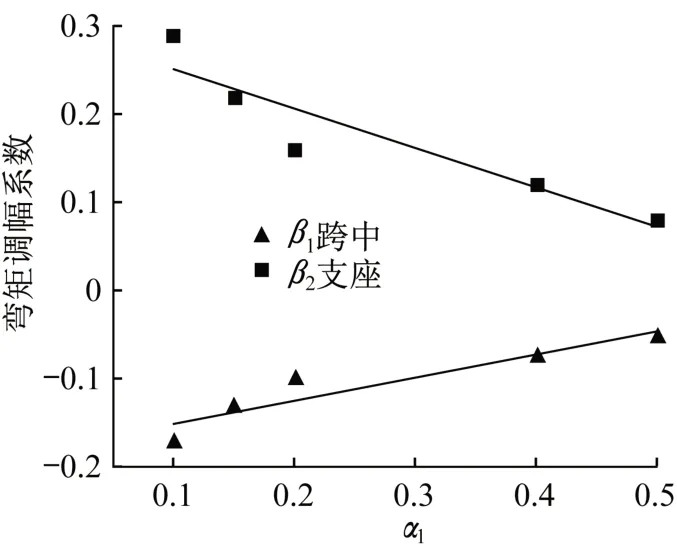
圖4 α1～β1及α1～β2擬合曲線Fig.4 Fitting curve ofα1～β1 andα1～β2

經擬合之后得到以α1為自變量的負彎矩區加固梁達到極限狀態下的β1的公式：

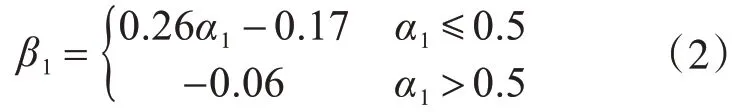
上述擬合公式中相關系數R2為0.88。

以α1為自變量的負彎矩區加固梁達到極限狀態下的β2的公式：

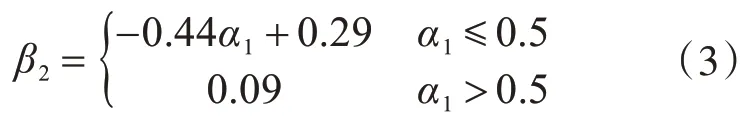
上述擬合公式中相關系數R2為0.86。

由表5可見，負彎矩區加固梁的第二段彎矩調幅系數β1或β2均隨著CFRP黏結長度的增加基本不變，即為恒定值。

表6為正彎矩區加固梁在不同α2下達到極限狀態時的彎矩調幅系數。由表6可知，隨著α2的增加，正彎矩區加固梁的跨中彎矩調幅系數β3及中支座彎矩調幅系數β4基本逐漸增大，其中β3增幅在-0.08～-0.17之間，β4增幅在0.13～0.28之間。在α2達到最優比值0.6后，β3與β4基本保持不變。

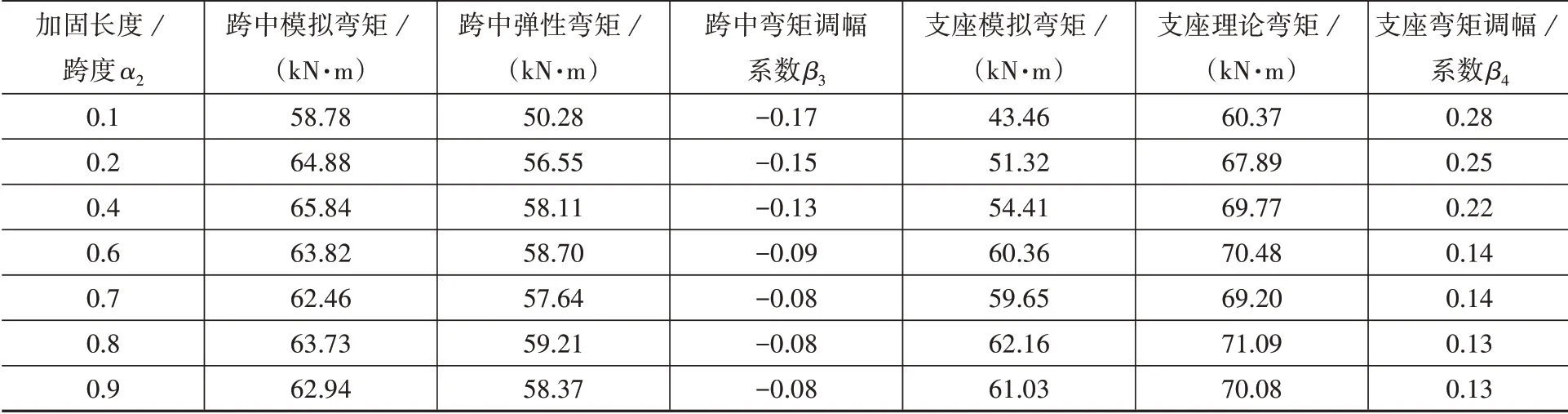
表6 不同α2時極限狀態下模擬彎矩值和理論彎矩值Table 6 Key bending moment values in limit state under differentα2

將正彎矩區加固梁的α2～β3及α2～β4的試驗點分成兩段，第一段α2≤0.7，第二段α2＞0.7。圖5為以α2為橫坐標，以β3，β4為縱坐標，得到的第一段正彎矩區加固梁α2～β3及α2～β4的試驗點分布。

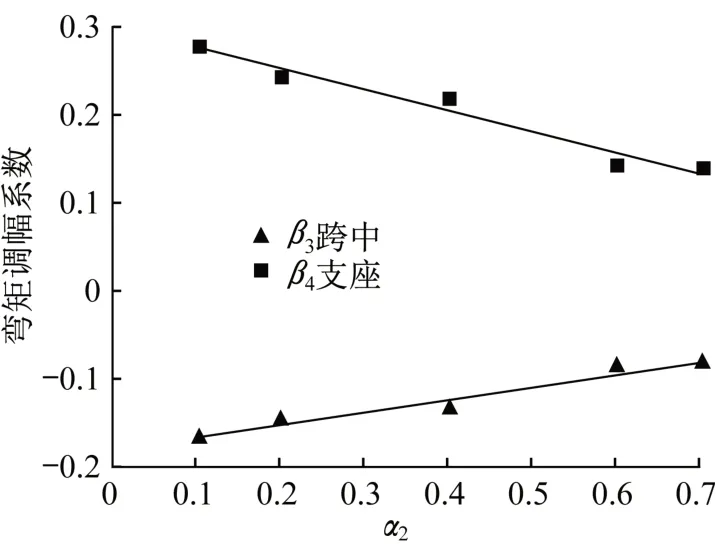
圖5 α2～β3及α2～β4擬合曲線Fig.5 Fitting curves ofα2～β3 andα2～β4

經擬合之后得到以α2為自變量的正彎矩區加固梁達到極限狀態下的β3的公式：

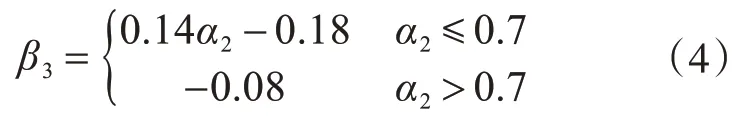
上述擬合公式中相關系數R2=0.96。

以α2為自變量的正彎矩區加固梁達到極限狀態下的β4的公式：

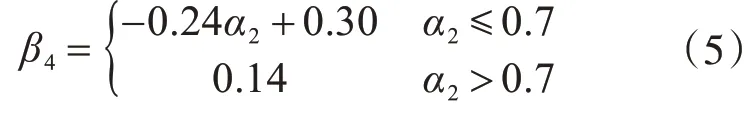
上述擬合公式中相關系數R2為0.96。

由表6可見，負彎矩區加固梁的第二段彎矩調幅系數β3或β4均隨著CFRP黏結長度的增加基本不變，即為恒定值。

綜上，負彎矩區加固梁的最優比值α1為0.4，建議極限狀態下跨中彎矩調幅系數β1按式（2）取值，中支座彎矩調幅系數β2按式（3）取值；正彎矩區加固梁的最優比值α2為0.6，建議極限狀態下跨中彎矩調幅系數β3按式（4）取值，中支座彎矩調幅系數β4按式（5）取值。

4 公式的應用及正確性驗證

為了進一步說明公式的應用及正確性，本文對公式進行了應用說明，并收集了國內外外貼CFRP加固RC連續梁的試驗數據，將試驗彎矩與調幅后的彎矩進行對比，以驗證公式的正確性。

表7、表8分別為負彎矩區及正彎矩區加固RC連續梁的關鍵數據，其中ME1為調幅后的跨中彎矩，MT1為跨中試驗彎矩；ME2為調幅后的中支座彎矩，MT2為中支座試驗彎矩。限于篇幅，表7、表8僅利用文獻［10］、［17］的試驗數據進行驗證分析。

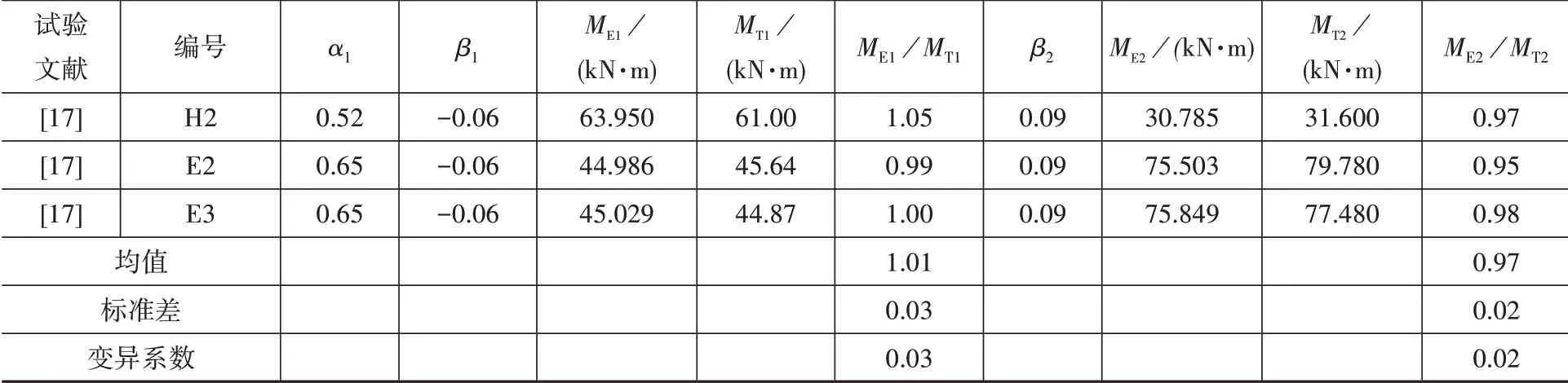
表7 負彎矩區加固梁彎矩計算值與試驗值對比Table 7 Comparison between calculated moment and test moment of negative strengthened beam

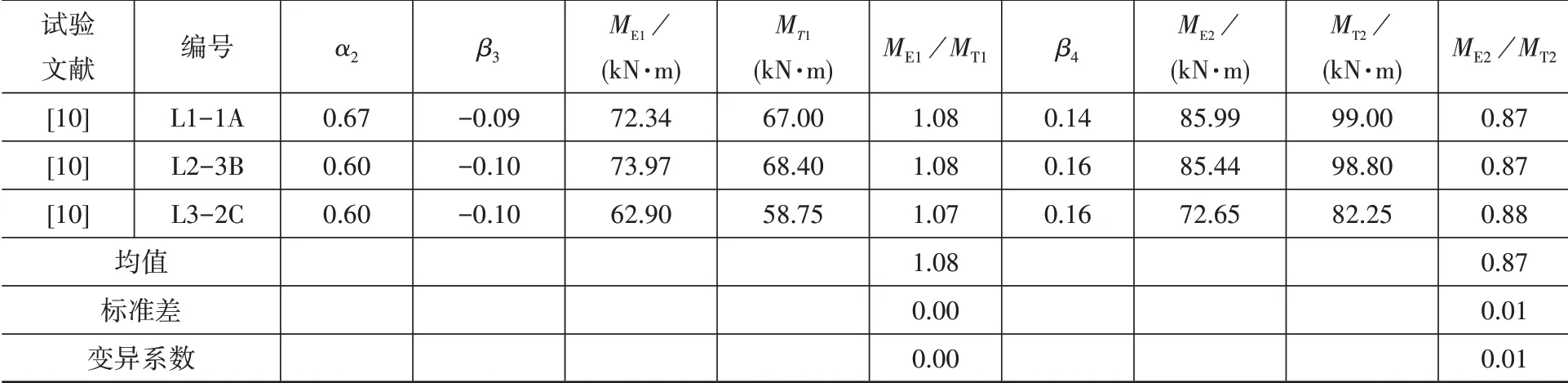
表8 正彎矩區加固梁彎矩計算值與試驗值對比Table 8 Comparison between calculated moment and test moment of positive strengthened beam

ME1的計算過程如下：首先由規范算出跨中理論彎矩Me1；其次根據試驗梁的實際情況算出黏結長度與跨度的比值；再根據比值套用本文擬合的公式，得出彎矩調幅系數；最后由彎矩調幅系數及跨中理論彎矩Me1得出ME1。經調幅后的中支座彎矩同理。

表7中的ME1及ME2由以上方法計算而來；Me1、Me2、MT1、MT2取自文獻［17］；表8中的Me1、Me2由力學方法計算而來，ME1及ME2根據以上方法計算，MT1、MT2由文獻［10］中的支座反力與相應跨度相乘而來。

從表7及表8可見，雖經調幅后的彎矩與試驗彎矩相比有一定誤差，但最大誤差不超過13%，仍在可接受范圍之內。故可得經調幅后的彎矩與試驗彎矩較吻合，即本文所擬合的公式具有一定的參考價值。

5 結 論

本文完成了外貼CFRP加固RC連續梁抗彎性能參數影響分析，提出了連續梁極限狀態時跨中及中支座彎矩調幅系數隨CFRP黏結長度與梁跨度比值變化的公式并進行驗證，得到主要結論如下：

（1）建立了外貼CFRP加固RC連續梁的有限元模型；數值分析結果表明：連續梁的屈服荷載隨著CFRP黏結長度的增加而增加，極限荷載隨著CFRP長度的增加先增加后基本不變，位移延性系數隨著CFRP長度的增加而減小。

（2）在簡化的基礎上，本文建議負彎矩區加固梁中CFRP黏結長度與梁跨度最優比值α1為0.4，正彎矩區加固梁中CFRP黏結長度與梁跨度最優比值α2為0.6；

（3）本文分別提出了負彎矩區加固連續梁中CFRP黏結長度與梁跨度之比α1和彎矩調幅系數β1、β2的關系公式及正彎矩區加固連續梁中CFRP黏結長度與梁跨度之比α2和彎矩調幅系數β3、β4的關系公式。通過試驗數據驗證分析，表明本文擬合的公式具有一定的參考價值。