砂泥巖混合填料濕化變形與沉降計算方法

云海浪， 韓文喜， 王 波， 張日華， 胡倫俊

(1.成都理工大學環境與土木工程學院， 成都 610059； 2.成都理工大學地質災害防治與地質環境保護國家重點實驗室，成都 610059； 3.河北建設勘察研究院有限公司， 石家莊 050000； 4.中國建筑西南勘察設計院有限公司， 成都 610000)

西南地區砂泥巖填料作為混合填筑材料，由于雨水的侵入作用使得該填筑體強度降低，經常發生濕化變形，對工程存在巨大安全隱患。目前，很多學者對軟巖和堆石料濕化變形特性進行研究。其中，劉輝[1]采用雙線法對變質軟巖軸向濕化變形和濕化體變規律展開分析，并通過擬合提出濕化變形經驗公式；殷坤垚等[2]對風干和飽和狀態軟巖填料進行試驗，通過分析圍壓對濕化變形規律的影響，得出濕化變形發展分為兩個階段；李青山等[3]對巴東組土料進行不同壓實度、不同圍壓的濕化變形試驗，得出濕化變形隨濕化點偏應力增大而增大，附加軸向應變隨圍壓增大而減小；丁艷輝等[4]對土石壩堆石料展開快速濕化三軸試驗，主要研究堆石料濕化變形的過程、特性及發生機制。隨著濕化變形在機場地基處理中成為重點，部分學者對砂泥巖類填料的濕化變形機制進行研究。王勝杰[5]闡明填筑體在濕化條件下的沉降機理并提出避免措施；付泓銳[6]通過砂泥巖三軸剪切試驗，探究周期性飽水作用對飽和砂泥巖混合料抗剪特性的影響；楊洋[7]提出了周期性飽水砂泥巖混合料的壓縮試驗方法，得出砂泥巖混合料的壓縮流變計算方法。

由于濕化變形對填筑體的變形、穩定帶來巨大困擾，學者在濕化變形機理的基礎上對變形量以及變形量計算方法展開研究。趙振梁等[8]對斜心墻堆石壩砂巖粗粒料采用單線法進行中型三軸濕化變形特性試驗，提出濕化變形數學模型。周雄雄等[9]采用單線法對粗粒料進行試驗，提出濕化體變與濕化軸變比值的計算方法和濕化軸變與濕化應力水平的雙曲線關系。楊培浩等[10]將濕化軸向應變分為由圍壓引起的應變和由偏應力引起的應變兩部分，分析其規律提出濕化變形計算公式。介玉新等[11]認為在某一應力狀態下的濕化變形是由兩部分，由材料本身剛度引起的濕化變形可用雙線法確定，由濕化引起的附加變形可通過單線法結合雙線法確定。

為研究西南地區砂泥巖濕化變形規律以及濕化后沉降變形，以成都天府國際機場砂泥巖填料為研究對象，使用GDS三軸試驗儀對直徑為300 mm、高度為600 mm的試樣展開濕化變形研究。通過室內試驗得出砂泥巖濕化變形計算方法，結合分層總和法進行沉降變形計算，并通過數值模擬進行驗證。

1 砂泥巖混合料濕化變形試驗

1.1 試驗材料

本次試驗所用土料取自成都天府國際機場T2航站樓南側附近，均為砂泥巖填料。顏色呈紫紅、磚紅，砂泥結構互層，節理發育明顯。根據現場試驗得出砂泥巖最優配比為7∶3，現場砂泥巖填料的天然含水率為2.68%。最優含水率為10.1%，最大干密度為2.01 g/cm3，現場級配曲線如圖1所示。

圖1 級配曲線圖

1.2 試驗方案

試驗所用砂泥巖混合料的相應級配、含水率與現場填料保持一致。試樣均為直徑300 mm、高度600 mm，最大粒徑為60 mm。本次濕化變形飽和樣采用飽和水頭法[12]進行飽和，注水水壓為350 kPa，水流從試樣底部注入，從試樣頂部出水口流出，直至流入水量與溢出水量相等為止。結合相關文獻[1-2，13-14]設計試驗方案如表1所示(未設置平行試驗)。

表1 試驗方案

1.3 試驗儀器與試驗步驟

本次試驗使用最新引進英國的GDS三軸試驗儀，試驗裝置主要由壓力室、軸向加壓設備、圍壓施加系統、體積和孔隙壓力量測系統和計算機控制與分析系統幾部分組成，如圖2所示。該套系統吸取了先進的機械制造工藝和自動控制技術，量測、控制精度高且實現了數字化操作。試驗主要步驟如下。

圖2 GDS三軸儀

(1)填料加工：在實驗室經過風干、碾碎、過篩，根據現場填料所使用的砂泥巖配比和級配制作砂泥巖顆粒試樣原料，配置所需含水率。

(2)試樣制備：制作直徑為300 mm，高度為 600 mm 的試樣，如圖3所示。根據試樣密度計算，分別稱取各級粒徑下填料質量，并配置相應含水率進行充分攪拌。試樣分6層擊實，每層裝入等量土料，使用擊實錘對每層擊實，達到每層要求高度 10 cm 時，對表面進行拋毛處理，減少人為因素降低試樣強度。

圖3 試樣制備

(3)裝樣：將壓力室放到加載架上，使加載中心與試樣中心、壓力室活塞桿中心在中軸線上，安裝位移傳感器、孔壓傳感器，關閉孔壓控制器閥門、壓力室排水孔。

(4)試驗設置及運行：將位移傳感器歸零，圍壓調至300 kPa，根據試樣要求應力水平為0.25、0.5、0.75的軸向偏應力值。

(5)終止試驗：該試驗全過程以應變速率為 0.1 mm/min 施加軸向偏應力，直至軸向應變達15%視為完成試驗[15]，破壞后試樣如圖4所示。

圖4 剪切破壞后試樣

2 結果分析

2.1 濕化應力應變曲線

整理試驗結果作干樣和濕樣的應力應變曲線圖，如圖5所示，軸向應變以壓縮為負，圍壓為300 kPa。

圖5 干樣與飽和樣應力應變曲線圖

由圖5可知，干樣在300 kPa圍壓下峰值偏應力為1 200 kPa，根據此數據可確定濕化試驗所施加的應力，為最大偏應力的0.25、0.5、0.75。在飽和樣剪切試驗中，施加約50 kPa的周圍壓力，水流從試樣底部注入，從試樣頂部出水口流出，直至流入水量與溢出水量相等，認為其達到飽和要求，然后在300 kPa進行固結剪切破壞。分析圖中應力應變曲線可得出的結論如下。

(1)干樣的最大破壞偏應力為1 200 kPa，而飽和樣的最大破壞偏應力為750 kPa，干樣濕化后，其強度下降了約1/3。

(2)砂泥巖干樣的應力應變曲線呈軟化型；飽和試樣的應力應變曲線一直位于干樣的下方，呈現出S型。結合姜景山等[15-16]、左永振等[17]利用CT手段研究濕化變形，分析其原因可能是由于水的侵入，軟化和潤滑了粗粒土顆粒，顆粒間產生滑動、破碎，顆粒位置發生重新調整，導致土顆粒的強度降低，削弱了應變硬化。因此隨著應變的繼續增長，應力漸漸趨向于一條直線。

2.2 濕化應力水平對濕化變形的影響

砂泥巖混合料在0.25、0.5、0.75的應力水平下浸水的變形時間曲線如圖6所示。

從圖6可以看出，在施加相應的應力水平的前2 000 s(33 min)內，試樣迅速產生變形，該階段變形快是因為施加荷載，且施加的荷載越大，變形越大。(在干樣的三軸剪切試驗中已確定干樣在300 kPa圍壓下的峰值破壞應力為1 200 kPa，因此試樣在相應應力水平下不會發生破壞。)

圖6 砂泥巖填料在不同應力水平下的變形時間曲線

保持試樣圍壓、應力水平不變，監測記錄位移數據，發現試樣在經過5 000 s(80 min)左右后，位移數據基本不會發生變化。待位移數據穩定后開始向試樣注水，可以發現趨于穩定的試樣開始繼續發生變形，經過7 h的浸水濕化變形后重新穩定，此時可以看出試樣的出水孔在均勻、穩定的出水，可以認為試樣的濕化已經完成。砂泥巖填料干樣、濕樣與濕樣分別在0.25、0.75應力水平下的應力應變曲線如圖7所示，試驗可得出以下結果。

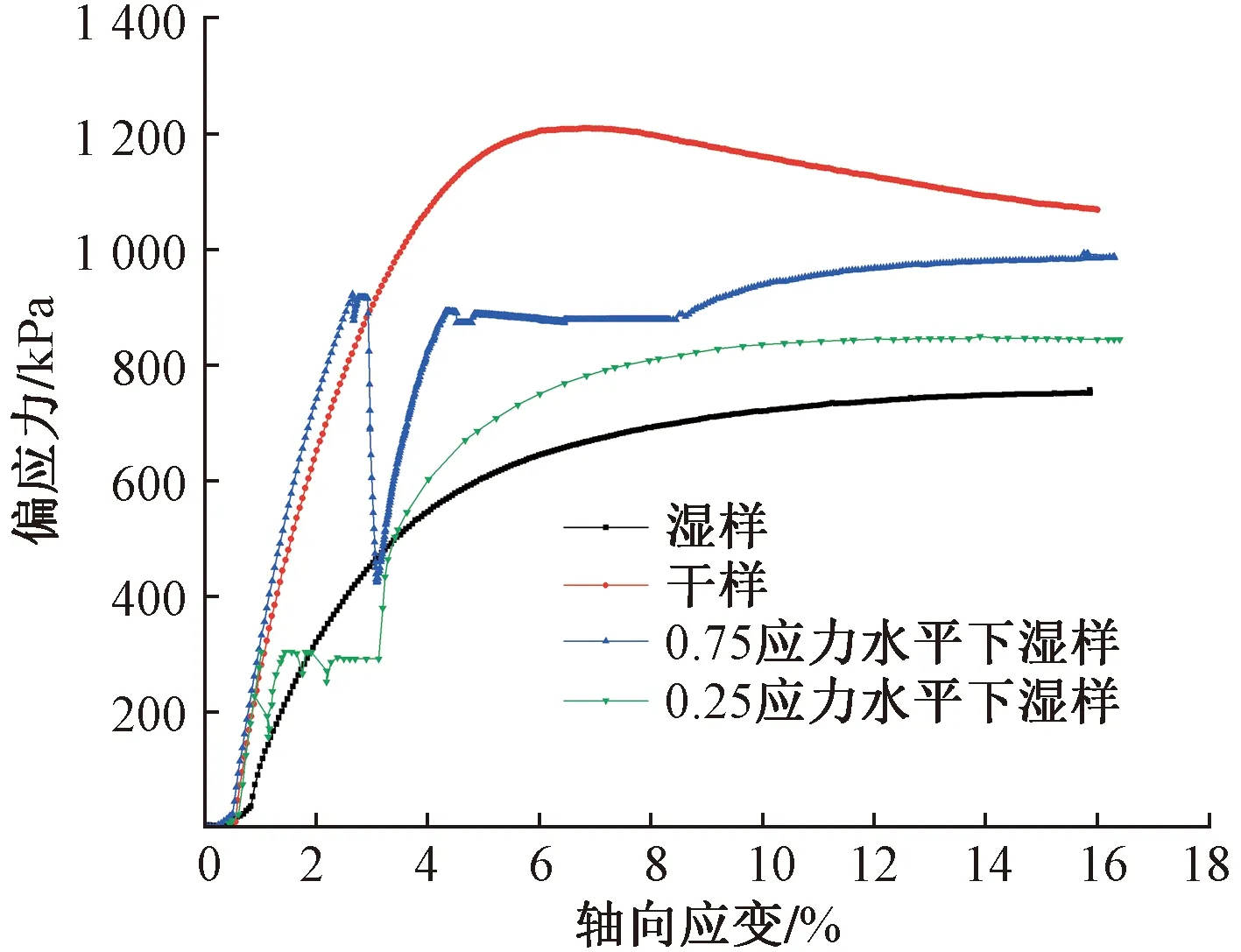
圖7 0.25、0.75應力水平下濕樣與干樣、濕樣的應力應變曲線

(1)砂泥巖填料在三軸壓縮試驗中的應力應變行為最初遵循干樣的應力應變曲線，在經受浸水濕化后遵循濕樣的應力應變曲線。

(2)砂泥巖填料在0.25、0.75應力水平下，其直線部分為濕化變形期間，在此期間，水在不斷地注入試樣濕化，可以發現應力水平越大，其濕化變形量越大。當應力水平下濕樣開始濕化時，其偏應力會發生驟降，分析原因可能是水的注入致使試樣內部孔隙水壓力升高，使軸向壓力驟降；偏壓力的下降幅度與圍壓、應力水平有關，圍壓越大、應力水平越高，其偏應力下降幅度越大。

試樣在注水后發生的變形直至穩定，在此期間發生的變形量認為是濕化變形，砂泥巖填料在不同應力水平下的濕化變形如圖8所示。

從圖8可以發現，砂泥巖填料在注水初期的變形增長相對較快，用不到20%的變形時間發生整體80%的變形量，而后變形放緩慢慢趨于穩定。另一方面，在同一圍壓下，濕化變形量隨著濕化應力水平的增大而增大，在應力水平較大時，濕化變形增加的幅度也比較大。一些學者分析其中原因，應力水平越高時，試樣在注水條件下的顆粒間的接觸、錯動、滑移越大，內部應力越大，造成的顆粒破碎、顆粒軟化越劇烈[18-19]。此外泥巖土性較軟，強度比砂巖強度差，在較大應力水平下會更容易破壞。

圖8 砂泥巖填料在不同應力水平下的濕化變形

為了探究濕化應力水平對濕化變形的影響，將砂泥巖填料在不同應力水平下的濕化變形統計出來，不同應力水平下濕化變形如表2所示。

表2 不同應力水平下濕化應變

分別采用指數型、線性、對數型、乘冪型關系對濕化變形和應力水平擬合，其擬合效果如表3所示。

表3 不同擬合類型下擬合效果表

從表3可以看出，濕化變形量與濕化應力水平用指數形式擬合效果最好，表達式如式(1)所示：

εw=aebs

(1)

式(1)中：εw為濕化變形量，mm；a、b為與材料、圍壓有關的參數；s為應力水平；e為自然常數。

可以得出，濕化變形量與濕化應力水平從經驗法上講是符合指數型關系的。可以根據相關試驗得到a、b值，算出單次濕化變形量。

3 考慮濕化變形的回填區域沉降變形分析

3.1 考慮濕化變形的沉降變形機理

通過對成都天府國際機場飛行區大鐵(東區)表層、地面、水位、孔隙的監測點分析，回填區域的沉降變形可分為原地面沉降變形、填筑體沉降變形、濕化變形。沉降變形受到上覆荷載、土體性質、地下水位等條件的影響。具體可分為以下4部分。

(1)瞬間變形：在土體受荷初期發生，土體受到荷載發生剪切變形形成的沉降，變形所用時間短、速率快，堆載高度和軟土厚度對其影響很大。

(2)主固結變形：隨后由土體內部孔隙水壓力的消散引起的沉降變形，占總沉降變形的大部分。

(3)濕化變形：因為降雨或者其他因素導致的地下水位升降，由于水的浸入濕化作用[18-19]，使土顆粒軟化并潤滑，使原先穩定的顆粒接觸狀態變得不穩定，顆粒位置重新調整，接觸得更為緊密，導致變形增大，但軟化和潤滑所導致的強度降低要大于擠密作用所帶來的強度提高，最終使粗粒土在濕化后強度降低。

(4)次固結變形：在填筑結束后較長一段時間內，填筑體相當于固定荷載，由于土中超孔隙水壓力基本消散完成，在有效應力不變，土體顆粒之間仍發生緩慢移動造成土體的微量變形沉降。

3.2 考慮濕化變形的分層總和法計算

分層總和法假定土體為各向同性彈性體，以彈性力學的應力應變為基礎來計算，忽略了土體的塑性變形，因此算出的沉降變形比實際地基沉降變形要小。在實際工程中，土體受到三個不同方向的應力，地基沉降變形包括豎向沉降變形和側向變形兩種。計算土體深度越深，側向變形越大，因此性需要乘以修正系數來矯正計算的總沉降量。但盡管如此，因為實際工程地質條件的復雜性，考慮到地下水位回升對影響范圍內土體產生的影響，提出考慮濕化變形的分層總和法計算沉降變形。在分層總和法的基礎上加上由式(1)提出的濕化變形計算方法，即

S=S1+S2

(2)

(3)

S2=aLebs

(4)

式中：S為沉降變形，mm；S1為分層總和沉降變形，mm；S2為濕化變形，mm;e1i為根據第i層的自重應力平均值從e-p曲線上得到相應的孔隙比；e2i為根據第i層的自重應力平均值與附加應力平均值之和從e-p曲線上得到相應的孔隙比；Hi為第i分層土的厚度；s為應力水平；a、b為與材料、圍壓有關的參數；L為地下水位影響砂泥巖填料深度(通過現場監測得到)。

選取由于地下水位上升產生變形的表層點BC792，其附近鉆孔XK3024上覆有14 m厚的砂泥巖填料。根據分層總和法算出在天然狀態下的沉降變形量S1，如表4所示。

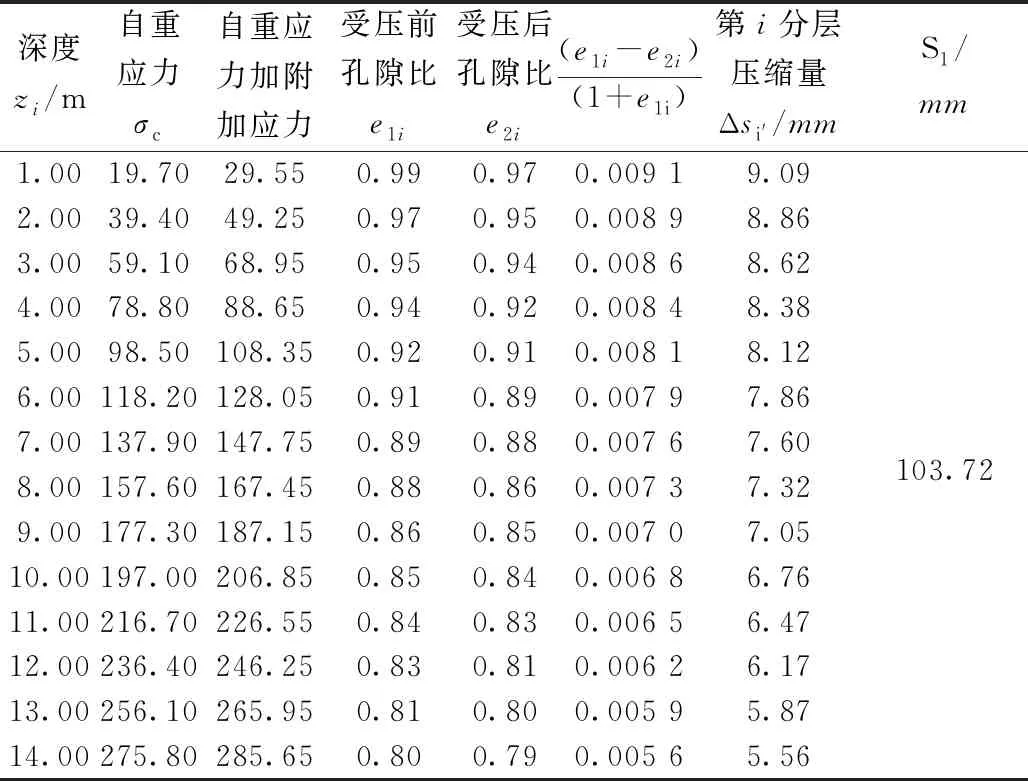
表4 分層總和法計算表

濕化變形沉降量S2=aLebs，由2.2節可知a=0.004 8、b=3.006，根據監測可知在2019年5—7月的地下水位進入填筑體高度為2 m，因此L=2，得到S2=17.5 mm。總沉降變形量S=S1+S2=121.22 mm，與實測BC792的沉降量相差4.52 mm，根據經驗其誤差在允許誤差范圍內。

通過地下水進入填筑體高度和式(2)考慮濕化變形的分層總和計算方法得到飛行區(東區)沉降變形如表5所示。

表5 飛行區(東區)沉降變形表

從表5中可以看出，考慮濕化變形的分層總和法的差值占比為-12.64%～17.47%。證明了考慮濕化變形的分層總和法的半經驗的數學公式針對成都天府國際機場沉降變形計算是相對準確的，可以用來計算回填區域的濕化變形。

4 考慮濕化變形的回填區域沉降變形數值模擬

PLAXIS數值模擬法可以設置施工工序，通過監測水位數據可以將地下水位變化趨勢體現出來。其本構模型中雙曲線模型可根據土體濕化前后力學性質改變，通過地下水位線的變化來確定發生濕化變形的土體范圍，根據力學性質的改變來計算其濕化變形。因此選擇PLAXIS數值模擬法進行砂泥巖填料濕化變形的模擬。PLAXIS的不足在于雙曲線模型存在8個特征參數，參數的選取對于性質的敏感性尚未探討。

4.1 本構模型選擇

通過對PLAXIS中本構模型的梳理，針對飛行區大鐵(東區)中砂泥巖填料、可塑性黏土和砂質泥巖的沉降變形和濕化變形計算選用Hardening-Soil模型，其優點在于該模型可以很好地模擬土體因應力狀態的變化其力學性質變化的情況，并可以模擬實際工程中地下水位回升對土的應力狀態造成的改變。

4.2 土體參數確定

通過現場試驗、室內三軸濕化試驗確定土體參數，在分步施工工序中設置變化的地下水位來模擬地下水位在工程實際發生的變化，模擬考慮濕化變形的填筑體的沉降變形。即可根據本構模型的特征參數來確定模型土體材料參數。

(1)m：剛度依據某個冪率的應力相關性；在軟土這種特殊情況下，使用m=1是現實的。

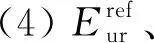
(5)c、ψ、φ：依據Mohr-Coulomb 模型的破壞模式確定。

模型土體等材料參數來源于《成都新機場詳勘總報告》《貨運區地區檢測報告》《成都天府國際機場飛行區工程全場地基處理工程施工圖設計說明》以及室內三軸濕化試驗，具體參數如表6所示。

表6 模型土體參數

4.3 數值計算結果與分析

確定模型土體參數后，將建好的數值模型生成網格，根據監測資料設置模型初始水位和荷載，初始工序設置完成后，開始進行數值計算。首先設置分步施工工序，根據水位監測點水位變化及對應時間確定時間間隔和地下水位線，時間間隔-水位變化如表7所示。

根據表7設置了8次工序，詳細設置如表8所示。

表7 時間間隔-水位變化表

表8 分步施工工序設置表

本次數值模擬是在模擬BC792點從2018年11月3日到2019年10月25日期間所發生的沉降變形量，時長共356 d。圖9所示A點即為BC792位置，B、C、D、E為其他表層監測點位置。

圖9 數值計算選取點A(BC792)

完成設置后開始進行數值模擬計算，變形的網格圖和陰影圖如圖10所示。

從圖10可以看出從A點到B點到C點，其沉降變形越來越小。歸結原因，距離A點越近，砂泥巖填料的高度越高，軟土的厚度也越厚，隨著地下水位線的變化其沉降變形越大。A點、B點、C、D點的變形-時間曲線如圖11所示，從下往上依次為A、B、C、D點曲線。

圖10 東區1-1′剖面沉降變形網格和陰影圖

圖11 A、B、C、D的變形時間曲線圖

根據監測數據BC792從2018年11月3日到2019年10月25的實際變形量為81.2 mm，數值模擬數值73.1 mm，誤差在允許范圍內。

4.4 實測值、理論計算與數值計算對比

飛行區大鐵(東區)的表層監測點實測沉降變形、理論計算沉降變形、數值計算沉降變形值得對比如表9所示。

從表9可以看出，考慮濕化變形的分層總和法的差值占比為-12.64%～17.47%，數值模擬的誤差占比為-11.97%～8.28%，其模擬效果相對較好。

表9 實測值、理論計算和數值模擬計算對比表

綜上所述，成都天府國際機場新近回填區域填料由于沒有經受降雨的影響且填筑高度高、未完成固結沉降，為確保濕化變形對工程不造成太大危害，選用理論公式計算、數值模擬、監測數據進行濕化變形分析，結果證明理論公式計算和數值模擬的可靠性，可以用來模擬濕化變形的，同時也證明了考慮濕化變形的分層總和法計算方法的適用性。

5 結論

通過砂泥巖填料的室內大三軸濕化試驗，初步分析研究了砂泥巖填料濕化作用下的變形特性，以及利用數值模擬和考慮濕化變形的分層總和法計算沉降變形，得出的結論如下。

(1)通過干樣和濕樣的三軸剪切試驗得到砂泥巖填料的應力應變曲線特征：干樣的應力應變曲線是軟化型；濕樣的應力應變曲線呈現出S形，其原因可能是水在顆粒之間的潤滑以及顆粒遇水崩解、軟化作用，使得飽和樣的抗剪強度小于干樣，削弱了應變硬化，因此隨著應變的繼續增長，應力漸漸趨向于一條直線。

(2)通過不同應力水平下的變形-時間曲線可以得到應力水平對濕化變形的影響：①砂泥巖填料在注水初期的變形增長相對較快，用不到20%的變形時間發生整體80%的變形量，而后變形放緩慢慢趨于穩定；②在同一圍壓下，濕化變形量隨著濕化應力水平的增大而增大，并通過指數擬合得到濕化變形計算公式。

(3)提出一種考慮濕化變形的計算沉降變形理論公式，并通過與監測數據對比證明了理論公式的準確性。

(4)通過PLAXIS中設置地下水位隨時間的變化以及濕化后土體性質改變的特點模擬回填區域考慮濕化變形的沉降變形，數值模擬成果證明理論公式計算和數值模擬的可靠性，可以用來模擬濕化變形；同時也證明了濕化應變與濕化應力水平呈指數型關系的半經驗數學公式的可靠性。