基于BP神經(jīng)網(wǎng)絡(luò)的大豆種子外觀品質(zhì)質(zhì)量檢測(cè)技術(shù)研究
魏 劍
(黑龍江省科學(xué)院,哈爾濱 150001)
大豆是主要的農(nóng)作物及經(jīng)濟(jì)作物之一。我國(guó)大豆種植面積和總產(chǎn)量都位居世界第四。大豆的生產(chǎn)形式通常為混合種植、混合收購(gòu),這種傳統(tǒng)的生產(chǎn)方式不能使優(yōu)質(zhì)大豆產(chǎn)品得到更好的經(jīng)濟(jì)收益。高蛋白、高品質(zhì)大豆的專門性種植、篩選是提高經(jīng)濟(jì)效益的有效途徑,這需要對(duì)大豆種子的質(zhì)量嚴(yán)格把關(guān)。20世紀(jì)80 年代,人工神經(jīng)網(wǎng)絡(luò)在人工智能領(lǐng)域成為研究熱點(diǎn)。神經(jīng)網(wǎng)絡(luò)是通過(guò)對(duì)人腦的模擬和抽象[1],從信息處理角度建立一種簡(jiǎn)單模型,由不同的連接方式形成不同類型的網(wǎng)絡(luò),是人工智能的高科技產(chǎn)物。由大量節(jié)點(diǎn)構(gòu)成網(wǎng)絡(luò),節(jié)點(diǎn)是一種函數(shù),稱為激勵(lì)函數(shù)。節(jié)點(diǎn)之間的連接是權(quán)重,激勵(lì)函數(shù)和權(quán)重的不同,影響網(wǎng)絡(luò)的輸出結(jié)果。
1 Matlab中神經(jīng)網(wǎng)絡(luò)的構(gòu)建
1.1 Matlab中典型的n維神經(jīng)元模型
Matlab中典型的n維神經(jīng)元模型如圖1。

圖1 典型n維網(wǎng)絡(luò)神經(jīng)元模型
其中,p1,p2,…,pn為神經(jīng)網(wǎng)絡(luò)的n個(gè)輸入,用n維向量表示為:
p=[p1,p2,…,pn]T
(1)
w1,w2,…,wn表示網(wǎng)絡(luò)權(quán)值,是輸入和神經(jīng)元之間的關(guān)聯(lián)度,設(shè)b代表神經(jīng)元閾值,則輸出表示為:
a=f(wp+b)
(2)
常見(jiàn)的傳遞函數(shù)f有線性函數(shù)、S函數(shù)、硬現(xiàn)幅(包括符號(hào)函數(shù))函數(shù)。在Matlab中,以上的傳遞函數(shù)—線性函數(shù)、S函數(shù)、硬限幅函數(shù)分別是purelin函數(shù)、logsig函數(shù)、hardlim函數(shù)。
1.2 神經(jīng)網(wǎng)絡(luò)的學(xué)習(xí)和訓(xùn)練
神經(jīng)網(wǎng)絡(luò)的學(xué)習(xí)和訓(xùn)練目的是調(diào)整合適的神經(jīng)元模型中的權(quán)值w和閾值b[2]。
學(xué)習(xí)是通過(guò)輸入層輸入信息,傳遞給中間層神經(jīng)元,最終到達(dá)輸出層。學(xué)習(xí)過(guò)程分為監(jiān)督學(xué)習(xí)和無(wú)監(jiān)督學(xué)習(xí),通過(guò)反復(fù)對(duì)比實(shí)際輸出和目標(biāo)輸出,調(diào)整權(quán)值和閾值,使實(shí)際輸出不斷接近目標(biāo)輸出。
訓(xùn)練分為批量式和漸進(jìn)式訓(xùn)練。其分別將目標(biāo)矢量和輸入矢量做統(tǒng)一一次性處理和調(diào)試或漸進(jìn)式調(diào)試。
2 BP神經(jīng)網(wǎng)絡(luò)的模式識(shí)別
BP神經(jīng)網(wǎng)絡(luò)是神經(jīng)網(wǎng)絡(luò)中最為廣泛使用的算法,產(chǎn)生于20世紀(jì)80年代,是對(duì)輸入、輸出對(duì)組訓(xùn)練的模型,是一種非循環(huán)的多級(jí)反復(fù)訓(xùn)練,具有廣泛的適應(yīng)性[3-4]。BP神經(jīng)網(wǎng)絡(luò)的基本結(jié)構(gòu)如圖2所示。
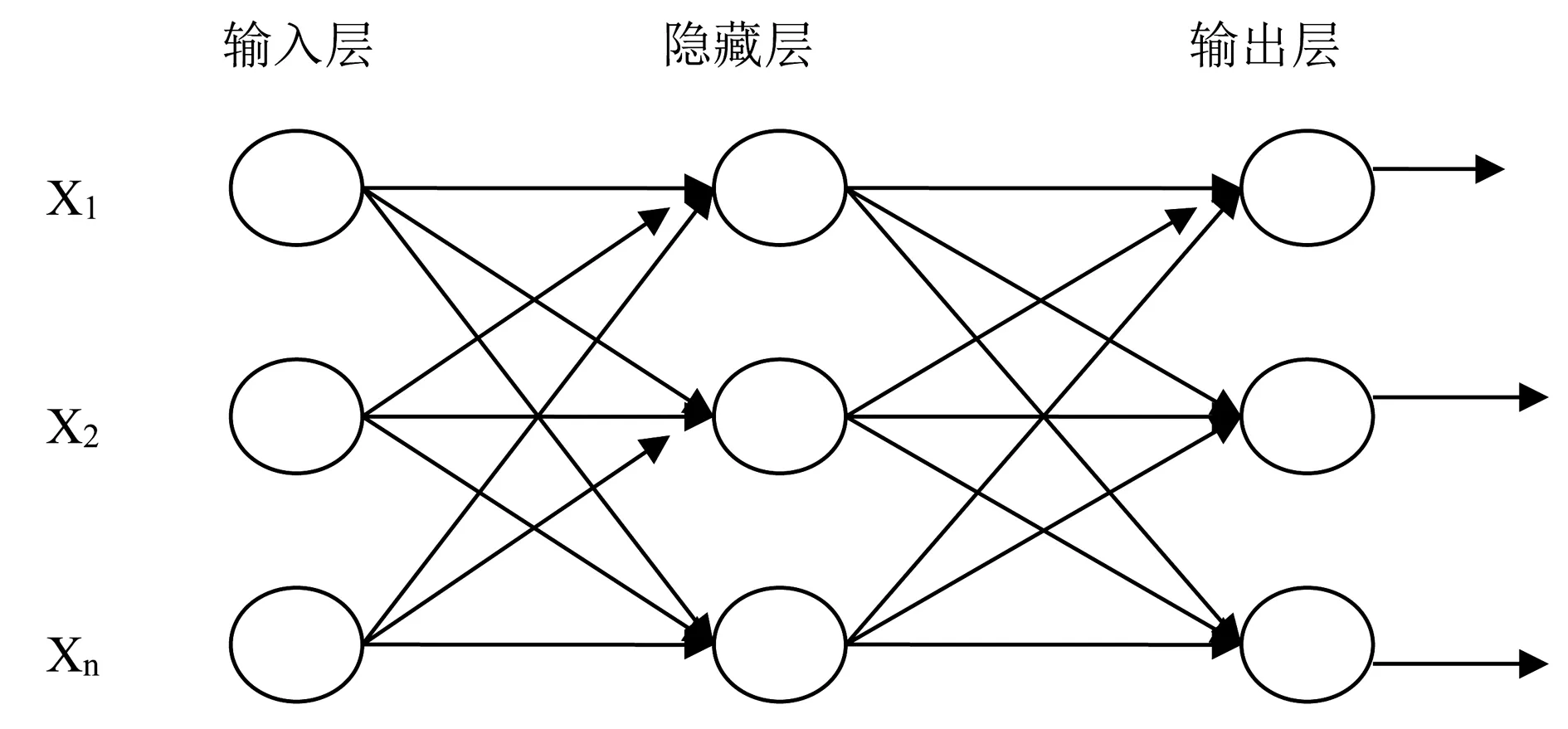
圖2 BP神經(jīng)網(wǎng)絡(luò)拓?fù)浣Y(jié)構(gòu)
BP神經(jīng)網(wǎng)絡(luò)分為輸入層、隱藏層、輸出層,通過(guò)反向?qū)W習(xí),調(diào)整權(quán)值和閾值,傳遞函數(shù)為S型函數(shù),訓(xùn)練中進(jìn)行歸一化,實(shí)現(xiàn)輸出量連續(xù)地分布在0~1,其基本思想為信號(hào)向前傳播和誤差向后傳播。Matlab中,BP神經(jīng)網(wǎng)絡(luò)的訓(xùn)練函數(shù)為train函數(shù)。訓(xùn)練前設(shè)置訓(xùn)練參數(shù),函數(shù)包括net.trainparam.epochs函數(shù):設(shè)置訓(xùn)練步數(shù);net.trainparam.show函數(shù):顯示訓(xùn)練結(jié)果間隔步數(shù);net.trainparam.time函數(shù):訓(xùn)練時(shí)間的設(shè)置;net.trainparam.goal函數(shù):訓(xùn)練的目標(biāo)精度;net.trainparam.min_grad函數(shù):訓(xùn)練允許的最小梯度值。
實(shí)現(xiàn)訓(xùn)練的基本函數(shù)為:[net,tr]=train(net,p,t),其中,p是輸入樣本矢量集,t是目標(biāo)樣本矢量集。
3 基于BP神經(jīng)網(wǎng)絡(luò)的大豆種子外觀品質(zhì)檢測(cè)
3.1 特征參數(shù)的降維處理
在特征提取環(huán)節(jié)中,提取了圖像顏色特征27個(gè),形狀特征8個(gè),紋理特征4個(gè),共39個(gè)特征參數(shù)作為反映的外觀特點(diǎn)的基本特征參數(shù),這些工作的完成,為種子質(zhì)量的檢測(cè)奠定了基礎(chǔ)。若將這些特征參數(shù)都作為BP神經(jīng)網(wǎng)絡(luò)的訓(xùn)練,則訓(xùn)練極易出現(xiàn)訓(xùn)練速度慢、網(wǎng)絡(luò)癱瘓的問(wèn)題。去除特征參數(shù)中一些次要項(xiàng)是必要手段,通過(guò)主成分析法(PCA)實(shí)現(xiàn)主要特征參數(shù)的選擇,使特征不僅數(shù)量減少,還具有獨(dú)立性和可靠性。
在Matlab中進(jìn)行主成分析的函數(shù)選用Princomp函數(shù),通過(guò)函數(shù)消除特征參數(shù)中的一些相關(guān)項(xiàng),分析步驟如下:計(jì)算相關(guān)系數(shù)矩陣;計(jì)算特征值和特征向量;計(jì)算主成貢獻(xiàn)率和累積貢獻(xiàn)率;計(jì)算主成分載荷。
Princomp函數(shù)實(shí)現(xiàn)如下:
PC=princomp(X)
[PC,SCORE,latent,tsquare]=princomp(X)
[PC,SCORE,latent,tsquare]=princomp(X)對(duì)數(shù)據(jù)矩陣X進(jìn)行主成分分析,給出各主成分PC、輸出得分SCORE、X的方差矩陣的特征值latent和每個(gè)數(shù)據(jù)點(diǎn)的統(tǒng)計(jì)量tsquare。根據(jù)主成分析得出的數(shù)據(jù)相關(guān)性表明,特征參數(shù)中不同顏色系統(tǒng)下的特征的獨(dú)立性不強(qiáng),經(jīng)過(guò)分析最終得到29個(gè)特征為主要參數(shù),保證了特征參數(shù)的獨(dú)立性和可靠性。
3.2 構(gòu)建BP神經(jīng)網(wǎng)絡(luò)
確定BP神經(jīng)網(wǎng)絡(luò)的網(wǎng)絡(luò)層和每層中神經(jīng)元的數(shù)目以及選擇初始權(quán)值和學(xué)習(xí)速率,激活函數(shù)選用S函數(shù),具體步驟如下:
采用主成分析法進(jìn)行特征參數(shù)的降維處理(上一節(jié)已做處理),將互相獨(dú)立的29個(gè)特征參數(shù)作為神經(jīng)元的輸入。
建立輸入矩陣,該矩陣的訓(xùn)練樣本數(shù)量為800,即800粒不同品種的大豆種子,200粒樣本作為測(cè)試集。
為了提高訓(xùn)練的速度,采用歸一化矩陣作為輸入矩陣,歸一化之后數(shù)據(jù)分布區(qū)間為[-1,1],通過(guò)函數(shù)premnmx實(shí)現(xiàn),Matlab程序語(yǔ)言為:[Pn,minp,maxp,Tn,mint,maxt]=premnmx(P,T),其中,minp,maxp代表原始輸入P中的最小和最大值;mint,maxt代表原始輸出T中的最小和最大值。
建立神經(jīng)元網(wǎng)絡(luò),調(diào)用 newff 函數(shù),網(wǎng)絡(luò)的輸入層為29 個(gè)神經(jīng)元,輸出層個(gè)數(shù)為 1 個(gè)節(jié)點(diǎn);Matlab程序語(yǔ)言為net=newff(MaxMinp,[s1,s2],{‘tansig’,‘logsig’},‘trainlm’),對(duì)應(yīng)層之間的映射關(guān)系和優(yōu)化函數(shù)實(shí)現(xiàn)網(wǎng)絡(luò)的訓(xùn)練。
網(wǎng)絡(luò)訓(xùn)練測(cè)試。
網(wǎng)絡(luò)的主要訓(xùn)練程序如下:
clear all;
p= xlsread(‘biao2.xls’);
p=p’;
t= xlsread(‘biao7.xls’);
t=t’;
[pn,minp,maxp,tn,mint,maxt]=premnmx(p,t);
xlswrite(‘maxp.xls’,maxp);
xlswrite(‘minp.xls’,minp);
xlswrite(‘maxt.xls’,maxt);
xlswrite(‘mint.xls’,mint);
[R,Q]=size(pn)
net=newff(minmax(pn),[s1,s2],{‘tansig’,‘purelin’},‘trainlm’);
%
net.trainParam.show=100;
net.trainParam.lr=0.2;
net.trainParam.mc=0.9
net.trainParam.epochs=2 000;
net.trainParam.goal=1e-6;
[net,tr]=train(net,pn,tn);
Y=sim(net,pn);
iw1=net.IW{1};
b1=net.b{1};
lw2=net.LW{2};
b2=net.b{2};
save netkohler net ;
由此建立了識(shí)別大豆種子質(zhì)量的輸入層神經(jīng)元個(gè)數(shù)為29的BP神經(jīng)網(wǎng)絡(luò)。
3.3 大豆種子四類病害識(shí)別研究
3.3.1 蟲(chóng)蝕病害的識(shí)別研究
如圖3為蟲(chóng)蝕大豆種子圖像,大豆種子蟲(chóng)蝕顆粒表面粗糙,形狀不規(guī)則,呈現(xiàn)鋸齒狀態(tài),顆粒顏色呈現(xiàn)深褐色。在蟲(chóng)蝕病害的識(shí)別中,選擇大豆種子圖像的顏色特征和形狀特征進(jìn)行識(shí)別。

圖3 蟲(chóng)蝕顆粒圖像
程序語(yǔ)言如下:
clear all
load(‘D:work netkohler.mat’);
test=xlsread(‘biao.xls’);
test=test’;
maxp=xlsread(‘maxp.xls’);
minp=xlsread(‘minp.xls’);
maxt=xlsread(‘maxt.xls’);
mint=xlsread(‘mint.xls’);
testn=tramnmx(test,minp,maxp);
S=sim(net,testn);
S = postmnmx(S,mint,maxt);
S=S’;
xlswrite(‘biao5’,[S]);
訓(xùn)練結(jié)果保存,選取200粒大豆種子,包括100粒蟲(chóng)蝕顆粒種子,100粒飽滿大豆種子作為測(cè)試集,測(cè)試訓(xùn)練網(wǎng)絡(luò)的識(shí)別率,測(cè)試部分結(jié)果如表1所示。

表1 大豆種子蟲(chóng)蝕顆粒識(shí)別結(jié)果
3.3.2 破碎顆粒的識(shí)別研究
在大豆的采摘、裝車、卸載等過(guò)程中,避免不了大豆種子因碰撞而破損,如圖4所示,破碎大豆種子與飽滿顆粒的大豆種子在顏色上不存在差異,差異主要體現(xiàn)在形狀上,因此圖像中特征選擇主要選取形狀特征進(jìn)行破碎顆粒的識(shí)別研究。

圖4 破碎顆粒圖像
將訓(xùn)練好的網(wǎng)絡(luò)進(jìn)行保存,同樣選用飽滿和破碎顆粒各100粒進(jìn)行測(cè)試,測(cè)試結(jié)果如表2所示。

表2 大豆種子破碎顆粒識(shí)別結(jié)果
破碎顆粒的訓(xùn)練結(jié)果為誤差達(dá)到-0.000 276 167。
3.3.3 霉變病害的識(shí)別研究
大豆種子發(fā)生霉變呈現(xiàn)種子脹大、豆子軟化、顏色加深的狀態(tài),如圖5為霉變大豆種子圖像。

圖5 霉變顆粒圖像
網(wǎng)絡(luò)的訓(xùn)練目標(biāo)為1e-006,即10的-6次方,最終訓(xùn)練誤差達(dá)到了8.53245e-007,測(cè)試結(jié)果如表3所示。

表3 大豆種子霉變顆粒識(shí)別結(jié)果
3.3.4 灰斑病害的識(shí)別研究
灰斑病的圖像進(jìn)行特征提取和選擇后,選用顏色特征,選取均方差最小的網(wǎng)絡(luò)測(cè)試,灰斑病的圖像如圖6所示。

圖6 灰斑顆粒圖像
訓(xùn)練目標(biāo)是1e-006,即10的-6次方,最終訓(xùn)練誤差達(dá)到了6.3295e-007。
同樣選用豆粒進(jìn)行測(cè)試,結(jié)果如表4所示。

表4 大豆種子灰斑顆粒識(shí)別結(jié)果
對(duì)大豆種子常見(jiàn)的四種病害的識(shí)別表明:構(gòu)建的BP神經(jīng)網(wǎng)絡(luò)能夠識(shí)別單類大豆種子病害,并且識(shí)別率較高;除了對(duì)破碎顆粒的識(shí)別率較低為83%外,其他單類缺陷的識(shí)別效果均良好。破碎粒識(shí)別率較差的原因可能是特征選擇造成。
大豆種子多項(xiàng)病害的檢測(cè)。針對(duì)單類大豆種子病害識(shí)別的訓(xùn)練網(wǎng)絡(luò)識(shí)別率較高,但在實(shí)際生產(chǎn)應(yīng)用中往往存在多種病害,因此建立能夠準(zhǔn)確識(shí)別多種病害并存的網(wǎng)絡(luò)是必要的,從而識(shí)別出優(yōu)質(zhì)大豆種子。
試驗(yàn)研究應(yīng)用 MATLAB 提取的大豆的 29個(gè)特征值構(gòu)建神經(jīng)網(wǎng)絡(luò)。構(gòu)建步驟如下:建立輸入矩陣,該矩陣的訓(xùn)練樣本數(shù)量為2 000粒,500粒樣本作為測(cè)試集。為了提高訓(xùn)練的速度,采用歸一化矩陣作為輸入矩陣,歸一化之后數(shù)據(jù)分布區(qū)間為[-1,1]。建立神經(jīng)元網(wǎng)絡(luò),調(diào)用 newff 函數(shù)[5],網(wǎng)絡(luò)的輸入層為29 個(gè)神經(jīng)元,輸出層個(gè)數(shù)為 5 個(gè)節(jié)點(diǎn)。Matlab程序語(yǔ)言為net=newff(MaxMinp,[s1,s2],{‘tansig’,‘logsig’},‘trainlm’),對(duì)應(yīng)層之間的映射關(guān)系和優(yōu)化函數(shù)實(shí)現(xiàn)網(wǎng)絡(luò)的訓(xùn)練。網(wǎng)絡(luò)訓(xùn)練測(cè)試。
參數(shù)的設(shè)置為:迭代步數(shù)為100,最大訓(xùn)練次數(shù)為1 000,學(xué)習(xí)速率為0.2,訓(xùn)練精度為1e-3。樣本數(shù)量較大,為了實(shí)現(xiàn)快速識(shí)別,選用合適的算法是關(guān)鍵,將常用的兩種算法進(jìn)行比較,選用Levenberg-Marquardt算法更為合適。
Fletcher-Reeves 共軛梯度算法。Fletcher-Reeves 共軛梯度算法簡(jiǎn)稱為FR法,根據(jù)已知點(diǎn)梯度形成共軛方向,并沿著此方向搜索到極小值點(diǎn)。對(duì)于初始點(diǎn)X,計(jì)算目標(biāo)函數(shù)f(x)的梯度。試驗(yàn)中設(shè)置迭代步數(shù)為100,最大訓(xùn)練次數(shù)為1 000,學(xué)習(xí)速率為0.2,訓(xùn)練精度為1e-3,訓(xùn)練結(jié)果如圖7所示。

圖7 Fletcher-Reeves 共軛梯度算法
訓(xùn)練結(jié)果為0.104 621,訓(xùn)練目標(biāo)是0.001。
Levenberg-Marquardt 算。Levenberg-Marquardt 算法是一種最優(yōu)化的算法[6],通過(guò)尋找一個(gè)使得函數(shù)值最小的參數(shù)向量實(shí)現(xiàn)訓(xùn)練,使用非線性的最小二乘算法,通過(guò)迭代尋優(yōu)。訓(xùn)練結(jié)果如圖8所示。

圖8 Levenberg-Marquardt算法
試驗(yàn)中設(shè)置迭代步數(shù)為100,最大訓(xùn)練次數(shù)為1 000,學(xué)習(xí)速率為0.2,訓(xùn)練精度為1e-3,訓(xùn)練結(jié)果為0.032 469 3。
試驗(yàn)結(jié)果表明,Levenberg-Marquardt算法的訓(xùn)練誤差更小,訓(xùn)練更精準(zhǔn)。利用Levenberg-Marquardt算法進(jìn)行網(wǎng)絡(luò)的訓(xùn)練,并將剛訓(xùn)練網(wǎng)絡(luò)保存,用飽滿大豆種子、蟲(chóng)蝕顆粒、破碎顆粒、霉變顆粒、灰斑顆粒、不同大豆混雜顆粒各100作為測(cè)試集,測(cè)試結(jié)果如表5所示。
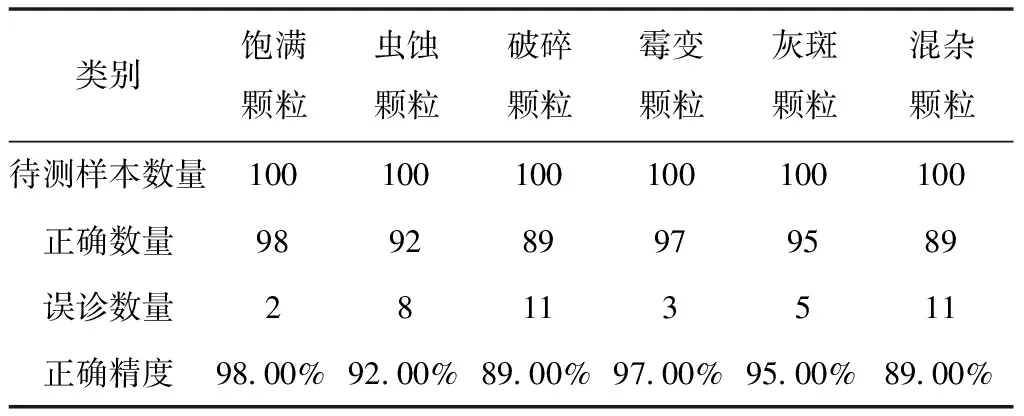
表5 大豆種子灰斑顆粒識(shí)別結(jié)果
4 小結(jié)
以上試驗(yàn)分析了神經(jīng)網(wǎng)絡(luò)及BP神經(jīng)網(wǎng)絡(luò)的結(jié)構(gòu)和學(xué)習(xí)訓(xùn)練過(guò)程,對(duì)特征參數(shù)進(jìn)行了主成分析法降維處理,降低了訓(xùn)練難度,提高了訓(xùn)練精度。采用BP神經(jīng)網(wǎng)絡(luò)的訓(xùn)練和測(cè)試,對(duì)單類大豆種子識(shí)別率很高。針對(duì)實(shí)際生產(chǎn),通過(guò)比較不同共軛梯度算法,采用Levenberg-Marquardt算法訓(xùn)練網(wǎng)絡(luò),誤差更小,達(dá)到了大豆種子多種缺陷的識(shí)別。

