基于機器學習與群智能算法的精車大螺距螺桿切削優化研究*

李 哲 叢瑋琦 付祥夫 田 盛 羅明明

(哈爾濱理工大學高效切削及刀具國家地方聯合工程實驗室,黑龍江 哈爾濱 150080)

大螺距螺桿類零件廣泛應用于重型立式車床以及大型壓力機中，起著緊固、連接、傳遞動力的作用，它的表面質量和精度將影響著機器的加工精度，是影響機床可靠性的重要部件[1]。大螺距螺桿的加工過程中的振動和刀具磨損問題，使得工件表面質量難以保證[2]。

已有研究表明，切削力和切削溫度是導致刀具振動與磨損的主要影響因素[3]。本文通過以切削力和切削溫度為目標，結合加工效率，進行多目標優化，利用優化的切削參數和刀具參數來抑制刀具的振動與磨損，以期改善工件的表面質量。

莊可佳等[4]建立了切削力和材料去除率的預測模型，以最大材料去除率和最小切削力為優化目標，得到最優切削參數組合，實現了鈦合金插銑高效穩定加工的目的。魯娟等[5]應用支持向量機和BP神經網絡結合的方法構建了銑削蠕墨鑄鐵表面粗糙度的預測模型，并對模型的預測精度進行驗證，可以很好地對表面粗糙度進行預測。劉洋等[6]利用神經網絡建立鉆削過程中切削力與切削參數之間的關系模型，與多元線性回歸建立的模型相比，神經網絡建立的模型預測精度更高。盧明明等[7]為了抑制三維橢圓振動切削過程中刀具的振動，改善工件的表面質量，建立表面質量與切削參數之間的數學模型，應用改進后的人工蜂群算法進行切削參數優化，得到更優的工件表面質量。馬廉潔等[8]采用粒子群算法改進BP神經網絡，建立了切削力、刀具利用率的優化目標函數，經過求解后進行實驗驗證，證明參數優化結果有效。Wang Z G等[9]采用遺傳算法對切削過程中材料去除率和表面粗糙度進行多目標優化，得到了最佳工藝參數，降低了工件的表面粗糙度。

以上學者在預測模型建立以及切削優化方面的研究給予本文啟示，對于建立精車大螺距螺桿切削力、切削溫度的回歸預測模型以及后續的參數優化具有參考意義。本文采用基于機器學習方法，以切削參數與刀具參數為變量，建立切削力和切削溫度模型。用群智能算法對建立的模型進行優化求解，最后對優化結果進行實驗驗證。

1 切削實驗及數據提取

1.1 大螺距螺桿精加工車削工藝分析

通常將螺距大于4 mm稱為大螺距螺紋，本文進行研究用到螺桿的螺距為18 mm，為了使切削力在切削刃上均勻分布，降低切削過程中振動的影響，大螺距螺桿在精加工階段采用軸向分層切削工藝，軸向分層切削時左刃或右刃全部參與切削。精車大螺距螺桿工藝如圖1所示。

圖1中，n為主軸轉速，vf為軸向進給速度；ap為切削深度，P為螺距，D1、D2和D分別為工件螺紋的小徑、公稱直徑和大徑，Zli、Zri為左、右刃單次加工余量，hDl、hDr為左、右刃單次加工時的切削厚度，bDl、bDr為左、右刃單次加工時的切削寬度，krl、krr分別為左、右刃切削時的主偏角。

1.2 實驗材料及設備

大螺距螺桿采用CAX6140車床進行加工，工件的材料為45#鋼，相關參數如表1所示，所用的刀具材料為W18Cr4V成型車刀，刀具參數如表2所示，刃口形狀為鈍圓刃，其中刀具后角以及刃口半徑在表3中給出。通過相關研究可知，刀具前角和刃傾角的變化對于切削力、刀具變形以及牙型精度存在影響，同時考慮到刀具的耐磨性和強度這兩個因素，最終確定刀具前角和刃傾角為0°時最能滿足生產加工的實際要求，不需要對其角度進行優化[10]。

表1 大螺距螺桿尺寸

表2 刀具參數

實驗所采用的設備如圖2所示，使用DHDAS5922動態信號測試系統對切削力信號進行采集，用到的傳

感器為PCB三向傳感器，通過THERMO VISION A40

熱像儀對切削區的切削溫度進行測量。

1.3 實驗方案及結果

通過切削實驗獲取不同參數條件下的切削力、切削溫度數值，考慮到切削參數和刀具參數的切削方案如表3所示。

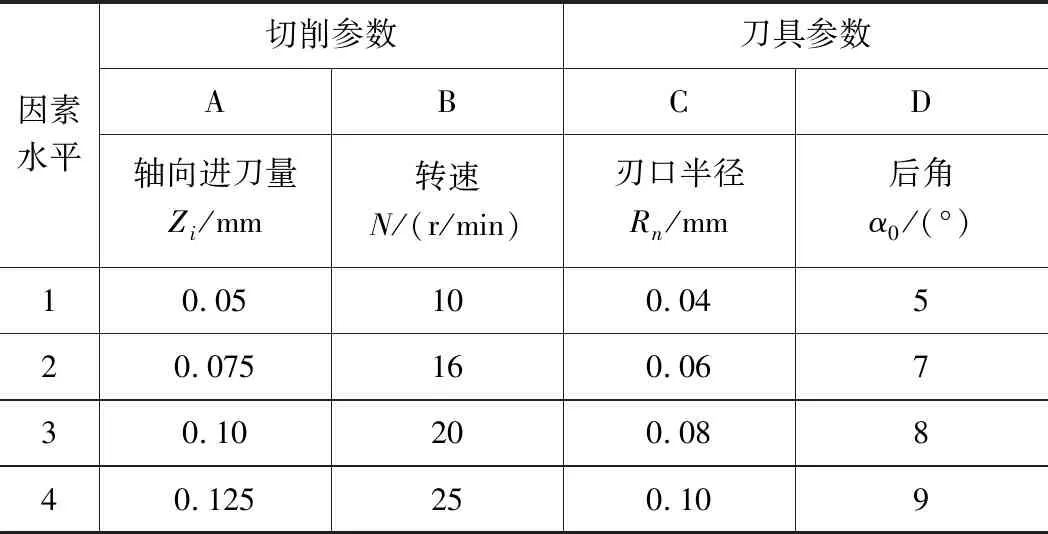
表3 正交試驗因素水平表

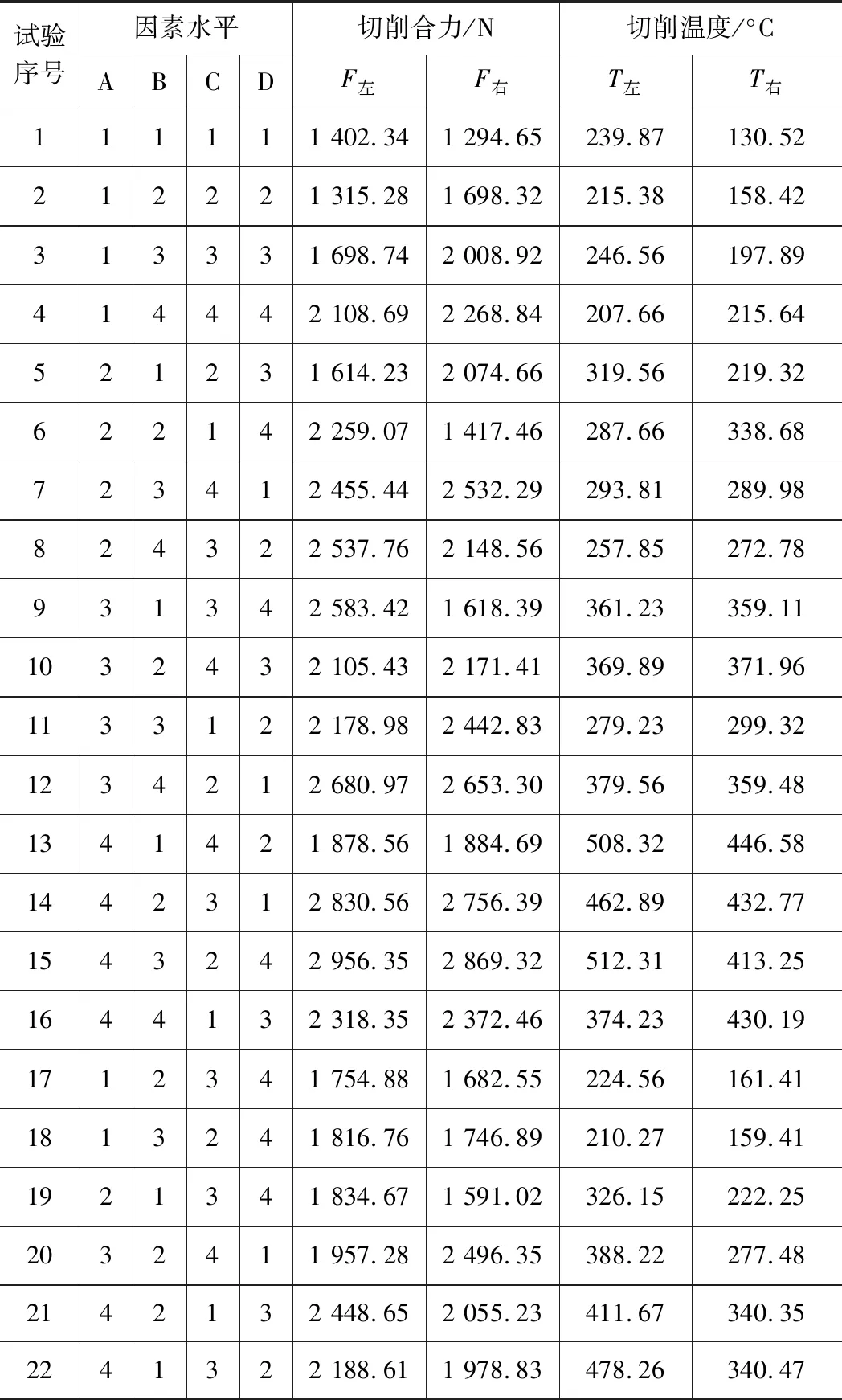
表4 實驗數據表

建立對應的切削參數與切削力、切削溫度的正交表，如表4所示，其中編號1～16為正交試驗組，用于回歸模型的建立；編號17～22為不同于正交試驗組的切削方案，作為預測組，用于對模型的預測效果進行檢驗。F左為左刃受到的切削合力，簡寫F左。

2 切削力與切削溫度建模

2.1 支持向量機回歸建模

支持向量機(SVM)可以用來解決分類以及回歸建模的問題，通過不同的核函數類型而完成對數據的回歸分析，建立輸入量與輸出量之間的關聯模型。經過對各項參數不同時的回歸效果進行比較，選用支持向量機的類型為ε-SVR，核函數類型為多項式核函數，設置ε-SVR的損失函數C的值為默認值1，損失函數w的值為0.1，核函數中的gamma函數的值為1。

2.2 回歸結果比較

為了證明機器學習在回歸分析中的精準性，同時采用傳統的回歸方法對數據進行擬合，獲得經過不同方法得到的切削力、切削溫度的擬合及預測情況如圖3和圖4所示。

得到切削力、切削溫度的擬合誤差分析如表5，表6所示，其中包括擬合與預測的平均誤差與最大誤差。

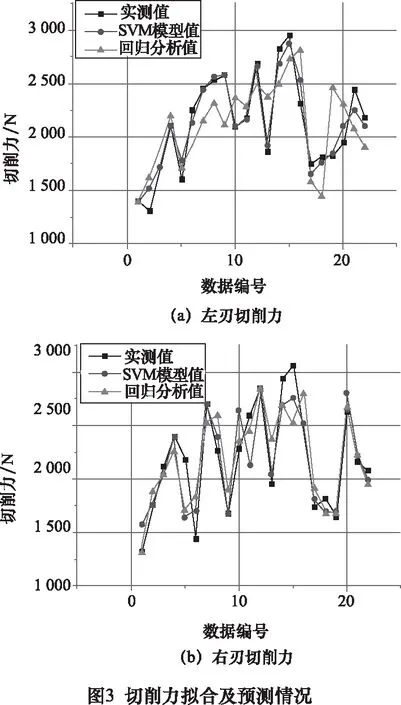
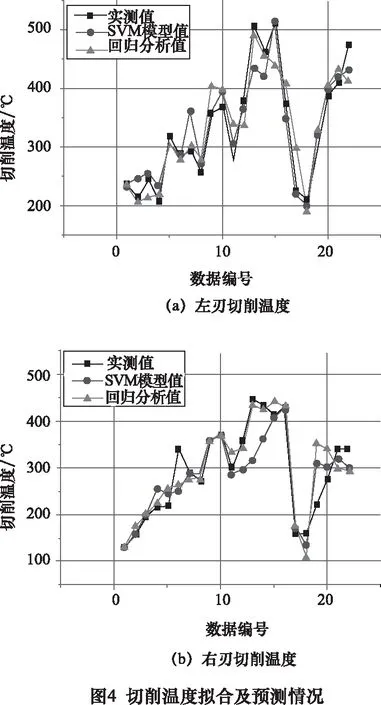
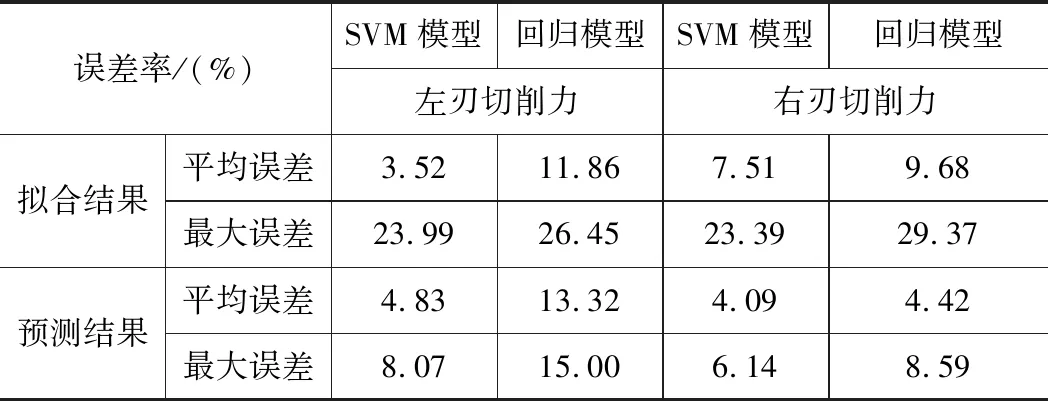
表5 切削力擬合誤差分析表

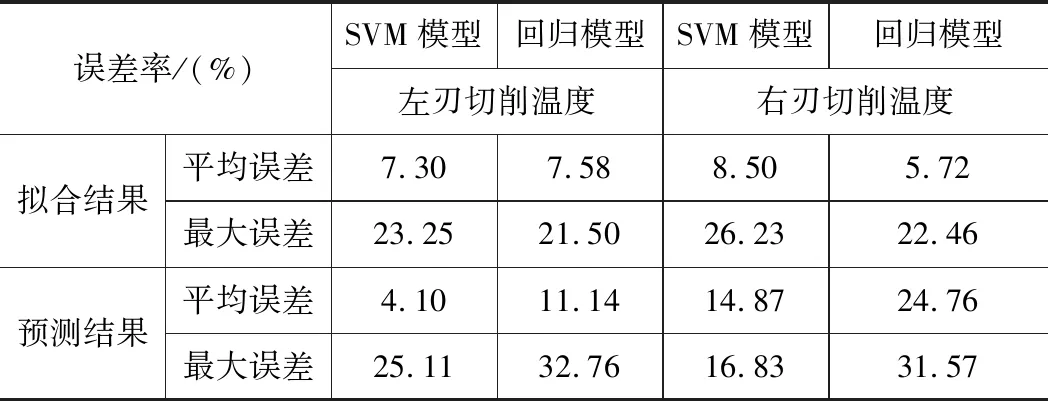
表6 切削溫度擬合誤差分析表

經過上述分析最終確定，支持向量機擬合后得到的模型更優，擬合與預測精度高，可以更好地反映切削參數與切削力、切削溫度之間的關系。

3 基于群智能算法的參數優化

3.1 多目標優化方程的求解

多目標優化中的難點是目標間的權重分配問題，本文基于MATLAB軟件，編寫出含有Pareto最優解的人工蜂群算法與粒子群算法的程序。多個目標同時處于最優解時即為Pareto最優解，也就是指資源分配的一種理想狀態。處于這種狀態下的解集為資源的最優分配，如果在這時想獲得某個目標的更優值，則會破壞資源分配的理想狀態，進而導致其他目標不再是最優解[11]。本文就是基于Pareto最優解理論進行的參數優化，解決了在多目標優化存在的目標間沖突的問題。

結合切削實驗以及以往切削加工中常用的參數范圍，最終確定參數優化的約束條件如下：

(1)主軸轉速約束條件：10 r/min≤n≤25 r/min。

(2)軸向進刀量約束條件：0.05 mm≤f≤0.125 mm。

(3)刀具后角約束條件：5°≤α≤9°。

(4)鈍圓刃口半徑約束條件：0.04 mm≤R≤0.10 mm。

將切削力與切削溫度作為優化目標，與此同時還需要考慮到材料去除率這一指標[12]。材料去除率如式(1)所示，最終確定優化目標方程如式(2)和(3)。

Q=v×ap×f

(1)

式中:v為切削速度，ap為切深，D為工件直徑，n為主軸轉速，v=π×D×n/1 000。

(2)

(3)

采用人工蜂群算法和粒子群算法進行多目標優化求解，算法相關參數的設置如表7所示。

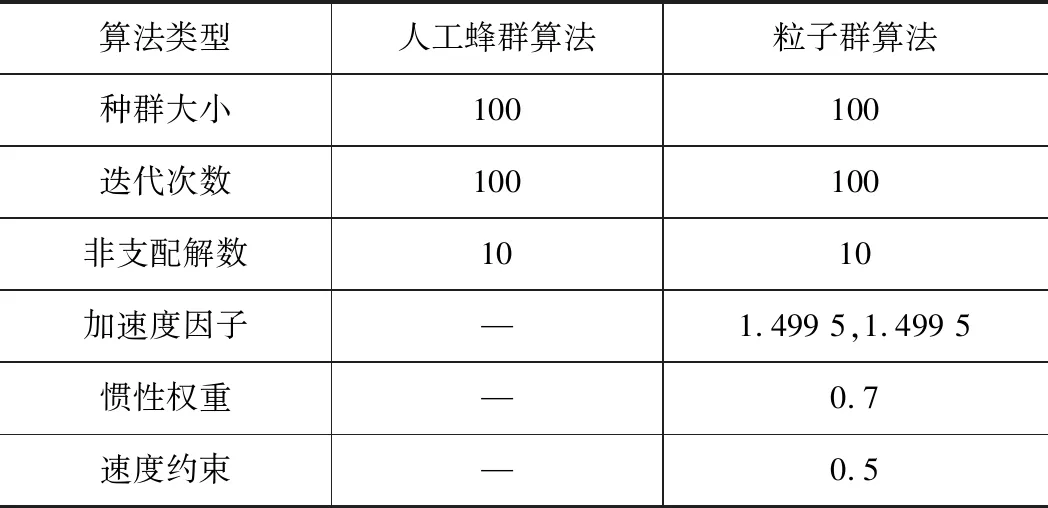
表7 算法相關參數

3.2 優化結果比較

經過參數優化求解后，得到人工蜂群算法和粒子群算法求解出的Pareto前沿分布如圖5和圖6所示。

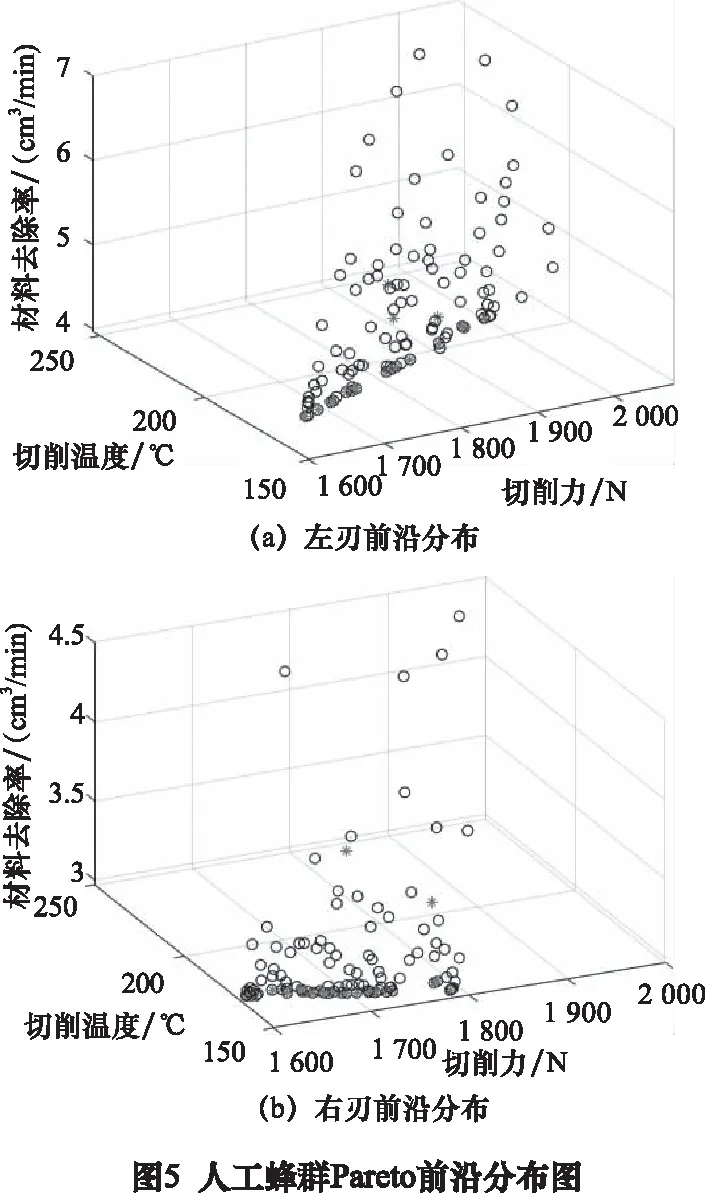
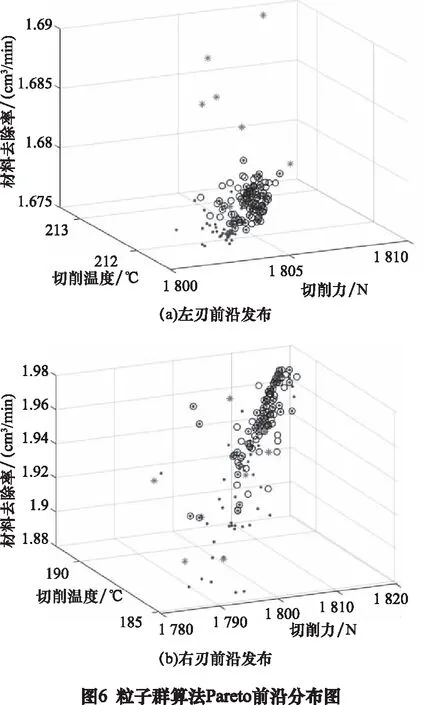
從二者的Pareto前沿分布圖中，提取出對應的前沿值，對不同算法的求解性能進行比較，采用求解時間、MID和SNS值3個指標進行評價，其中MID[13]代表Pareto前沿值與最小理想適應度值(0,0,0)的距離，SNS代表非支配解的分散水平，計算公式如(4)和(5)所示。

(4)

(5)

式中：N代表非支配解的個數，f1i、f2i、f3i代表Pareto前沿值中，第i個非支配解的3個適應度值。MID的值越小越好，該值越小，表明Pareto前沿值更靠近最理想適應度值。SNS表示Pareto非支配解的分散程度，數值越大，說明Pareto前沿值越分散。

經過計算后，得到兩種算法的各項性能指標如表8所示。

表8 算法的性能指標

最終選擇性能相對較好的人工蜂群算法求解出的參數作為精車大螺距螺桿的最優切削參數。確定左刃切削最佳參數為：轉速n=20 r/min，進給量f=0.05 mm，刀具后角α=6°，刀具刃口半徑R=0.06 mm；右刃切削最佳參數為：轉速n=16 r/min，進給量f=0.05 mm，刀具后角α=6°，刀具刃口半徑R=0.04 mm。

3.3 驗證實驗

為了驗證優化得到刀具參數和切削參數的有效性，需進行驗證實驗。工件參數和刀具參數如表1和表2所示，實驗儀器如表3所示，經過優化后的刀具參數(后角、刃口半徑)以及切削參數得到了更有效的值，相關參數在表9中列出。具體的切削方案如表9所示，其中方案一的刀具參數經過優化，方案二的切削參數經過優化，方案三為刀具結構和切削參數優化后的最優值，方案四為上文正交實驗方案中的參數，以此作為對照，對優化效果進行驗證。

對加工完的工件進行取樣處理，沿著軸線方向，從切入端向切出端依次標記，利用線切割機床將標記樣塊取下，利用超景深顯微鏡測量其左右螺紋面的表面粗糙度值，通過采集多次測量數據，對每個取樣的粗糙度值求取平均值，最終獲取螺紋面粗糙度參數測量結果。如圖7所示為螺桿表面粗糙度的測量方法。

表9 切削方案

提取出測量得到的表面粗糙度數值，得到不同切削方案下的樣塊左、右螺紋面粗糙度值，如圖8所示。

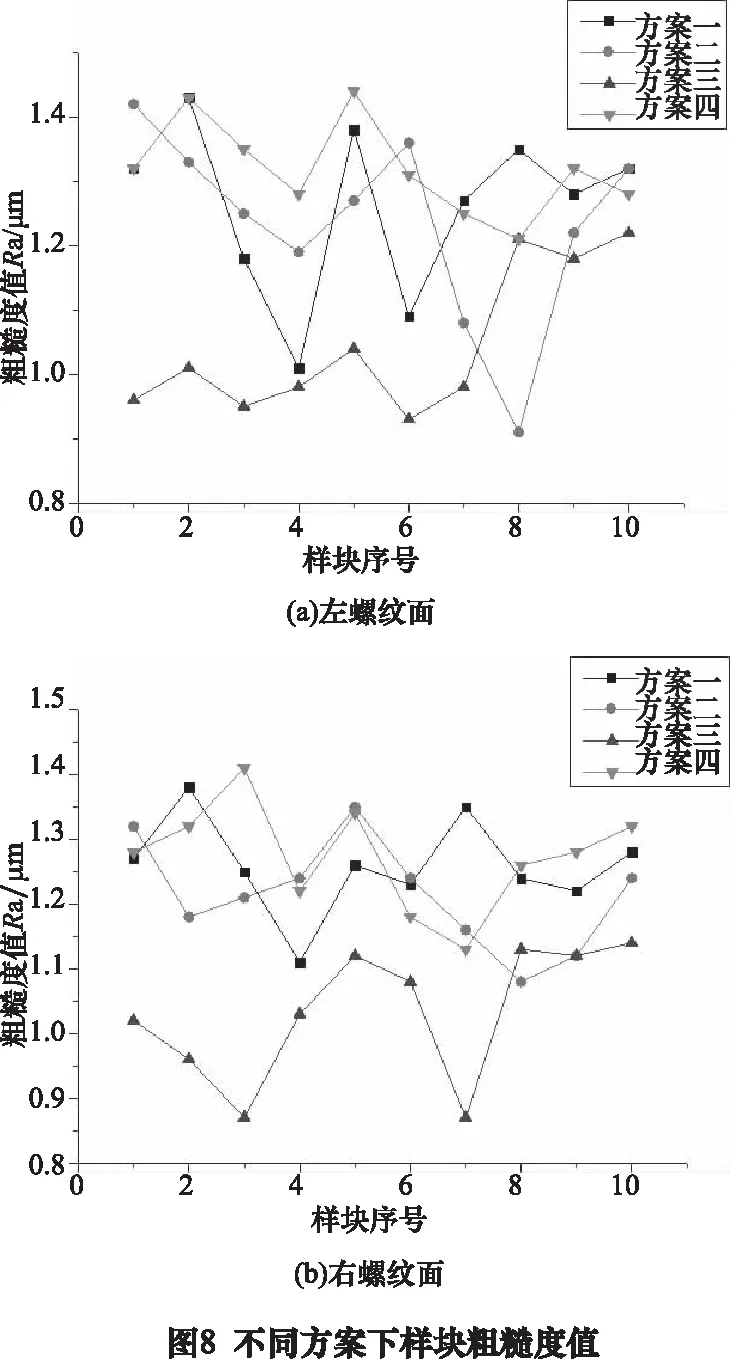
不同切削方案下左右螺紋面粗糙度平均值如圖9所示。

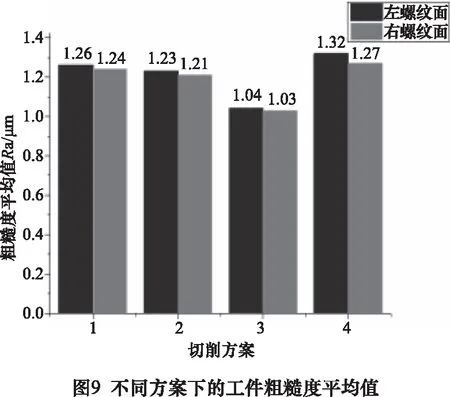
對通過不同切削方案得到的工件樣塊表面粗糙度平均值分析可知，經過切削參數優化后的方案三，獲得的工件樣塊表面粗糙度值更小，證明切削優化有效，經過切削優化后得到的工件表面質量得到改善。

4 結語

(1)運用支持向量機算法，對不同切削參數對應的切削力、切削溫度數值進行訓練，建立了擬合精度更高的回歸預測模型。

(2)采用人工蜂群算法與粒子群算法對切削力、切削溫度、材料去除率的多目標優化方程進行求解，得到切削參數和刀具參數的最優值；通過對不同算法的求解時間、MID值、SNS值這3項性能指標進行比較，確定人工蜂群算法的優化結果為最優解。

(3)進行精車大螺距螺桿驗證實驗，對獲得的工件表面粗糙度的測量結果進行對比，發現選用優化后的參數進行加工，工件表面粗糙度降低了20%，可以獲得更好的工件表面質量。