平行砂輪磨削圓弧頭立銑刀后刀面的軌跡算法*
唐 軍 馬忠寶 羅 斌 江 磊
(西南交通大學機械工程學院,四川 成都 610031)
圓弧頭立銑刀作為整體式立銑刀的一種類型,廣泛應用于復雜形狀零件的自由曲面加工制造,具有材料切除速率高和加工表面質量好的優點[1-2]。圓弧頭后刀面是圓弧頭立銑刀關鍵的結構之一,主要用于減少刀具和工件之間的摩擦,對刀具的使用壽命影響極大[3]。其磨削工藝的加工質量將直接影響圓弧頭立銑刀刃線和回轉輪廓的精度。立銑刀后刀面按刀具結構分為周刃后刀面和端刃后刀面。對于周刃后刀面,Pham T T等[4]根據形狀不同分為平面型、偏心型和凹面型3種形式,其中偏心型后刀面具有較大的刀尖角,刀尖強度大,具有良好的切削性能和加工表面質量[5]。平面型后刀面刃口強度介于凹面型和偏心型之間,應用最為普遍。李國超等[6]對上述3種形式的后刀面進行了刃磨工藝分析,給出了3種周刃后刀面刃磨砂輪初始姿態的求解模型;孫長富等[7]利用端截面游動坐標系法和幾何描述法對周刃平面型后刀面進行了建模計算;李光業等[8]描述了用碗形砂輪端面和平行砂輪周邊分別磨削周刃平面型后刀面的加工工藝分析,給出了磨削時砂輪刀位數學模型。針對端刃后刀面,劉建軍等[9]基于提出的圓弧頭通用刃線數學模型,研究了立銑刀端齒后刀面的磨削加工工藝分析并計算出了砂輪的運動軌跡和軸矢量;張瀟然等[10]針對圓弧頭立銑刀端齒后刀面后角和寬度的約束等問題,定義了一種后刀面約束曲線實現對端齒后角及后刀面寬度的控制。綜上,目前的磨削工藝主要側重于采用碗形砂輪端面進行平面型后刀面磨削,且對端刃和周刃后刀面磨削工藝研究是分段進行的,導致刀刃連接區域不光滑。
針對上述問題,本文研究了采用平行砂輪圓周面作為磨削區域的磨削工藝,并提出了周刃和端刃連續加工的圓弧頭立銑刀后刀面磨削軌跡算法。該算法不僅可加工周刃偏心型后刀面,而且通過周刃和端刃后刀面的磨削姿態連續變換,保證了后刀面的光滑過渡,提高了磨削加工效率、表面質量和精度。
1 圓弧頭立銑刀刀刃曲線建模
1.1 周刃建模
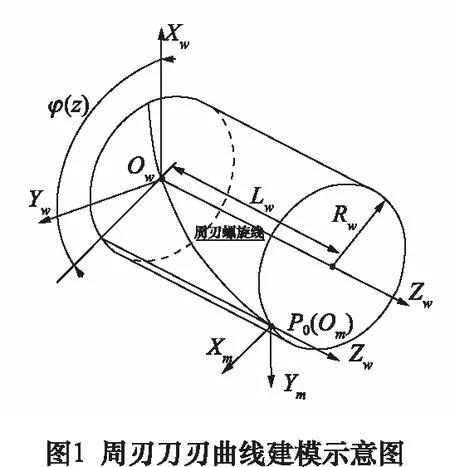
周刃刀刃曲線模型在許多文獻中均有描述[11-12]。本文建立以刀具回轉軸為Zw軸,以周刃起點所在的端面為XwOwYw平面,圓心為原點Ow的工件坐標系Ow-XwYwZw,如圖1所示。以Zw軸的坐標值z為自變量,則周刃上刀刃點P0坐標可表達為
(1)
式中:Rw為刀具回轉半徑;Lw為周刃長度;φ(z)表示點P0相對于Xw軸繞Zw軸的回轉角度。
1.2 端刃建模
建立以刀具回轉軸為Zd軸,以圓弧回轉體的底面為XdOdYd平面,以其圓心為原點Od的端刃坐標系Od-XdYdZd。則其轉換到工件坐標系的變換矩陣Td-w為:
(2)
本文將端刃曲線分為3個部分,分別在端刃坐標系下進行描述:
(1)圓弧回轉面曲線部分
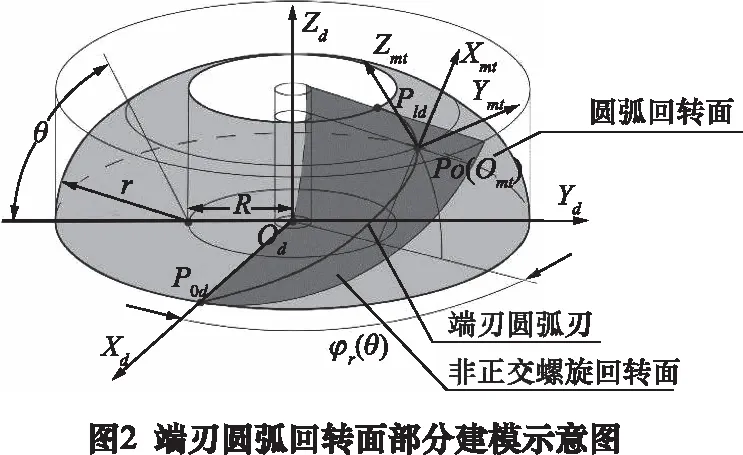
定義為由圓弧回轉面與非正交螺旋面求交線獲得的曲線P0dP1d,如圖2所示。則該段曲線上刀刃點P0坐標可表達為:
(3)
式中:自變量θ為緯度角;R為圓弧中心距;r為端刃圓弧半徑;φr(θ)表示刀刃點P0處回轉角。
(2)平面曲線部分
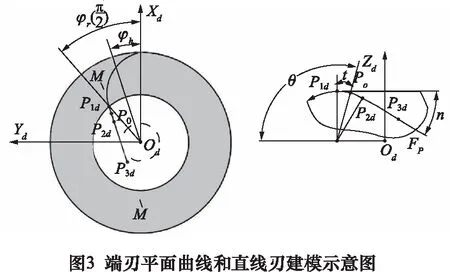
定義為在平面M上的一段圓弧曲線P1dP2d。如圖3所示。由式(3)可得圓弧回轉面末點P1d的坐標表達式,則該段曲線上刀刃點P0坐標可表達為:
(4)
式中:φh為表示平面M與Xd軸的夾角;η為直線刃內傾角。
(3)直線刃部分
定義為在平面M上的一直線段P2dP3d,如圖3所示。根據公式(4)可得平面曲線末點P2d的坐標表達式和切矢量Fp,引入自變量t,則該段曲線刀刃點P0坐標可表達為:
PP0d=PP2d+t·FP,0≤t≤lh0
(5)
式中:lh0為端刃直線刃長度。
1.3 后刀面坐標系及轉換
為了方便描述后刀面幾何參數和計算磨削軌跡,本文根據刀刃曲線模型,定義如下坐標系:
(1)周刃坐標系
定義為跟隨周刃的活動坐標系Om-XmYmZm,如圖1所示。其以周刃曲線上的點P0為坐標原點Om,以點P0對應的回轉體母線切線為Zm軸,以點P0對應的圓周切線為Ym軸。則有周刃坐標系轉換到工件坐標系的變換矩陣Tm-w為:
式中自變量z的取值范圍同公式(1)。
(2)圓弧回轉面坐標系
定義為跟隨圓弧回轉面曲線的活動坐標系Omt-XmtYmtZmt,如圖2所示。其以圓弧回轉面曲線上的點P0為坐標原點Omt,以點P0對應的回轉體母線切線為Zmt軸,以點P0對應的圓周切線為Ymt軸。則有圓弧回轉面坐標系轉換到端刃坐標系的變換矩陣Tmt-d為:
(7)
式中:自變量θ的取值范圍同公式(3)。
(3)平面曲線坐標系
定義為跟隨平面曲線的活動坐標系Ots-XtsYtsZts,如圖3所示。其為將圓弧回轉面曲線末點的坐標系Omt-XmtYmtZmt繞Ymt軸旋轉刀刃點P0對應的角度t,然后平移到平面曲線上的P0點得到。其中t的取值范圍為[0,η]。則有平面曲線坐標系轉換到端刃坐標系的變換矩陣Tts-d為:
(8)
式中:自變量θ的取值范圍同公式(4)。
(4)直線刃坐標系
定義為跟隨直線刃的活動坐標系Oms-XmsYmsZms,如圖4所示。其以直線刃磨削點P0為坐標原點Oms,Zms軸以平行于平面曲線末點的Zts軸,Yms軸平行于平面曲線末點的Yts軸。則有直線刃坐標系轉換到端刃坐標系的變換矩陣Tms-d為:
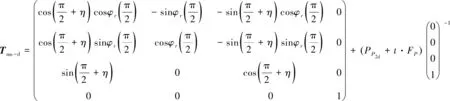
(9)
式中:自變量t的取值范圍同式(5)。
2 砂輪磨削后刀面軌跡計算
2.1 砂輪磨削姿態定義
為了方便計算和保證磨削的連續性,周刃和端刃后刀面的砂輪磨削姿態均根據刀刃曲線建模定義在對應的坐標系下。
(1)周刃偏心型后刀面的磨削姿態
根據周刃偏心型后刀面的磨削原理[6],令砂輪圓心Og在平面XmZm內,定義砂輪端面在平面XmZm內的投影與Xm軸的夾角為α(其由螺旋角β和周刃后角λm決定),如圖5所示。
(2)端刃圓弧回轉面后刀面的磨削姿態
如圖5所示,令砂輪圓心Og在位于平面XmtZmt內,定義砂輪圓周面在平面XmtZmt內的投影與Zmt軸的夾角為緯度角θ,且砂輪端面在平面XmtYmt內的投影與Ymt軸的夾角為圓弧回轉面后角λmt。
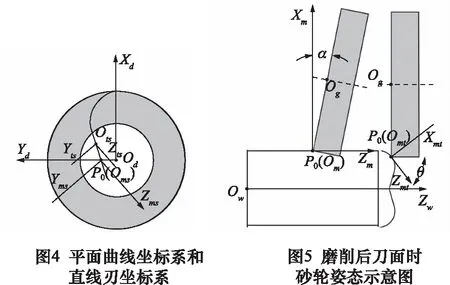
(3)端刃平面曲線和直線刃后刀面的磨削姿態
針對端刃平面曲線后刀面,令砂輪圓心Og位于Zts軸上,并且砂輪端面在平面XtsYts內的投影與Yts軸的夾角為平面曲線后角λts。
同理,針對直線刃后刀面,令砂輪圓心Og位于Zms軸上,并且砂輪端面在平面XmsYms內的投影與Yms軸的夾角為直線刃后角λms,如圖6所示。

2.2 后刀面連接處的砂輪磨削姿態過渡
根據上述磨削姿態定義可知,周刃和圓弧回轉面后刀面部分砂輪磨削姿態不一致。因此為了保證磨削的連續進行,需要設置砂輪磨削姿態的過渡。周刃末點即為端刃起點,該點處的周刃坐標系與圓弧回轉面坐標系重合。因此在此處坐標系下設置過渡方式為砂輪端面在平面XmtZmt內的投影與Xmt軸的夾角逐漸從α變為零,在平面XmtYmt內的投影與Ymt軸的夾角逐漸從零變化到圓弧回轉面后角λmt。如圖7所示。

2.3 砂輪磨削軌跡計算
砂輪磨削軌跡計算分別在對應的后刀面活動坐標系下進行,包括砂輪端圓中心點坐標Og和砂輪軸矢量Fg的計算。為了便于加工,可應用公式(2)和公式(6) ~ (9)將砂輪軌跡轉換到工件坐標系下表達。
(1)周刃后刀面
根據磨削姿態定義,并考慮到周刃到圓弧回轉面部分后刀面的過渡設置,可得在砂輪端圓中心點Og在周刃坐標系下的坐標可表達為:
Og_m=
(10)
式中:Rg為砂輪端圓半徑。
其砂輪軸矢量Fg在周刃坐標系下可表達為:
Fg_m=
(11)
(2)圓弧回轉面部分后刀面
根據砂輪磨削圓弧回轉面后刀面姿態定義,則有砂輪端圓中心點Og在圓弧回轉面坐標系下可表達為:
(12)
其砂輪軸矢量Fg在圓弧回轉面坐標系下可表達為:
(13)
(3)平面曲線部分后刀面
根據砂輪磨削平面曲線后刀面姿態定義,則有砂輪端圓中心點Og在平面曲線坐標系下可表達為:
(14)
其砂輪軸矢量Fg在平面曲線坐標系下可表達為:
(15)
(4)直線刃部分后刀面
定義直線刃后刀面的法矢為Fg0。當磨削直線刃部分后刀面時,為了防止砂輪與其他刀刃發生干涉,砂輪可繞矢量Fg0旋轉砂輪擺角μ。添加砂輪擺角后,砂輪軸矢量不變,同時對砂輪擺角μ進行線性過渡保證連續性,其表達為:
(16)
則砂輪端圓中心點Og坐標在直線刃坐標系下可表達為
(17)
其砂輪軸矢量Fg在直線刃坐標系下可表達為:
(18)
3 算法驗證
為了驗算所提出的砂輪磨削軌跡算法,本文進行了如圖8所示的流程驗證。其中圓弧頭后刀面砂輪磨削軌跡的計算和機床NC程序的獲取,是在VC++環境開發一套算法模塊來實現的。輸入圓弧頭后刀面相關幾何參數和工藝參數,根據提出的砂輪磨削軌跡算法,輸出其刀位軌跡文件;再以刀位軌跡文件為輸入,根據坐標變換進行后置處理,輸出數控機床的NC程序。其后置處理過程本文由于篇幅省略。
三維仿真則使用Vericut8.0來實現,選擇四刃圓弧頭立銑刀進行磨削軌跡仿真,其仿真數據及結果如表1~2。
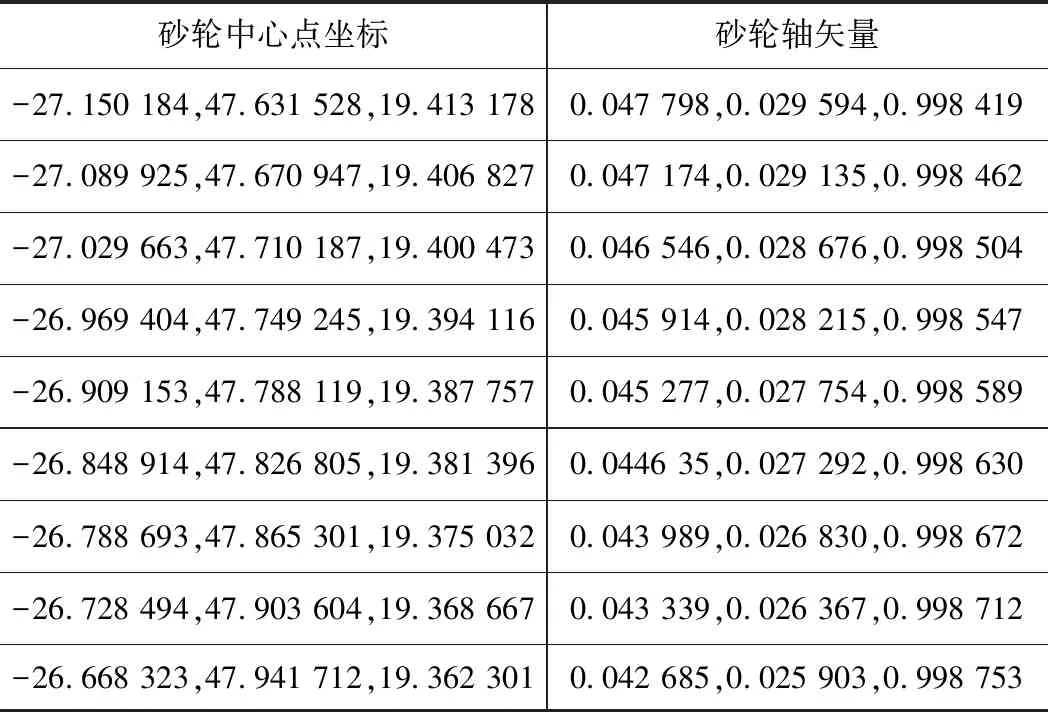
表2 部分磨削軌跡運算結果
在Vericut8.0中進行磨削仿真的結果如圖9所示。


在精利MD3015五軸聯動數控工具磨床上進行實際加工,并利用刀具檢測儀PG-1000進行刀具結構參數測量,結果如圖10所示。

4 結語
(1)建立了一種分段式且能保證各段之間光滑過渡的圓弧頭立銑刀刀刃曲線模型。
(2)根據周刃偏心型后刀面形成原理,將其磨削方式擴展到端刃部分,提出了一套保證砂輪姿態連續變換的周刃和端刃后刀面的砂輪磨削軌跡算法。
(3)通過磨削仿真和實際加工,驗證了該算法的正確性和有效性。

