高速列車橫向蛇行失穩的EEMD-CNN-LSTM預測方法

方明寬， 寧 靜， 陳春俊

(1. 西南交通大學機械工程學院，四川 成都 610031; 2. 軌道交通運維技術與裝備四川省重點實驗室，四川 成都 610031)

0 引 言

隨著我國高鐵的發展，其分布越來越廣泛，速度也在逐步提升，列車運行的安全性和穩定性就顯得尤為重要。而列車的橫向蛇行失穩，嚴重威脅到列車的安全運行。鐵道車輛的蛇行運動是一種自激運動，由于車輪踏面具有錐度，車輛運行過程中會出現左右輪徑不同從而產生蛇行運動[1]。車輛蛇行運動穩定性直接影響車輛的非線性臨界速度。高速車輛一旦發生蛇行運動失穩后，不僅會惡化車輛的運行性能，降低旅客的舒適度，使車輛各零部件上的動載荷增大，而且輪對會嚴重地撞擊鋼軌，損傷車輛及線路，甚至會造成脫軌事故[2]。

關于蛇行失穩，目前國內比較通用的定義是根據TB10761—2013《高速鐵路工程動態驗收技術規范》[3]和TB/T 3188—2007《鐵道客車行車安全監測診斷系統技術條件》[4]，判定高速列車轉向架橫向失穩的條件是轉向架構架橫向加速度信號經過0～ 10 Hz濾波后，其峰值連續6次以上（包括6次）達到或超過 8～ 10 m/s2的極限值。Souza A F D[5-6]等通過描述函數法研究列車蛇行運動，提出了蛇行失穩的發生經歷了正常、小幅蛇行和大幅蛇行3個過程。當列車發生蛇行運動，若列車運行速度不高，蛇行運動頻率低于車輛自振頻率時，列車車體、構架、轉向架的蛇行運動各振型的幅值會不斷減小，即蛇行運動收斂，此時，車輛的蛇行運動是穩定的，且幅值衰減越快，穩定的程度就越高。當列車以較高的速度運行，蛇行運動頻率與車輛自振頻率接近時，其振幅不斷增大，即發生了蛇行失穩，且幅值增大越快，失穩的程度就越嚴重。因此小幅蛇行有小幅收斂和小幅發散兩種演變趨勢。

隨著特征提取方法的不斷改善，越來越多的特征提取方法應用到高速列車橫向失穩分析中，崔萬里[7]通過樣本熵理論以及等距映射算法（isometric feature mapping，ISOMAP）對信號進行特征提取，然后通過最小支持向量（the least square support vector machine，LS-SVM）進行特征識別達到較好的效果。葉運廣[8-9]通過MEEMD進行特征提取與特征識別亦取得良好的效果。然而這些方式提取特征方式的計算過程復雜，從而導致其處理速度較慢，此外忽略了小幅蛇行的變化狀態。

基于以上問題，本文提出基于EEMD-CNN-LSTM橫向失穩預測方法。通過選取EEMD最優模態作為CNN-LSTM模型的預處理，能夠減少CNNLSTM的參數，使得計算模型更容易收斂。該方法結合了EEMD與CNN-LSTM優點，相對于傳統的特征提取方法，計算速度快，泛化能力更強，因此更加適用于高速列車這一類的復雜振動信號。

1 EEMD-CNN-LSTM算法原理

1.1 EEMD

EEMD是EMD的改進算法，其基本思想為通過添加白噪聲輔助信號來使得信號極值點分布均勻，并克服EMD分解中出現模態混疊的缺點。主要步驟如下：

1)將具有正態分布的輔助白噪聲信號加入待分解信號x(t)中得到X(t)；

2)將X(t)進行EMD分解，得到固有模態IMF分量；

3)重復步驟1)和2)，每次加入強度相同的白噪聲；

4)對 IMF 分量求平均值，得到最終 IMF 分量。

1.2 選取最優模態方法

本文基于信號的能量特征與計算模態相關系數方法提出挑選最優模態的算法，其綜合考慮了模態相關系數和能量特征兩個因素，因此相對于單一指標更為有效。

1.2.1 計算 EEMD 分解后的模態能量特征

長度為m的原始數據，通過EEMD分解為n階模態，并將模態降噪后得到模態矩陣C=[c1,c2,···,，大小為 n×m，其能量特征 E為1×n的向量，E=[e1,e2,···,en]，計算方式為：

1.2.2 計算 EEMD 模態的相關系數

長度為m的信號x經過EEMD分解后的得到n階模態，模態矩陣 C =[c1,c2,···,cn]，各階模態與x相關系數向量 R =[r1,r2,···,rn]，具體計算方法如下：

1.3 1D-CNN

一維卷積網絡 (one-dimensional convolutional neural network，1D-CNN)[10]其基本原理與普通的CNN類似，其主要區別在于1D-CNN卷積方向只有一個，而普通的CNN卷積方向有兩個，因此1DCNN主要用來建立時間序列模型，廣泛的應用于故障診斷中。其卷積運算為：

式中：X——輸入特征向量；

W——一維卷積核；

b——偏置量；

f——激活函數。

1.4 LSTM

LSTM（long-short-term memory）改善了 RNN梯度爆炸與梯度消失等問題，進而廣泛應用于構建序列模型。其算法原理見文獻[11]。

2 基于EEMD-CNN-LSTM高速列車橫向蛇行失穩預測方法

如圖1所示，基于EEMD-CNN-LSTM高速列車橫向蛇行失穩預測方法的具體步驟如下：

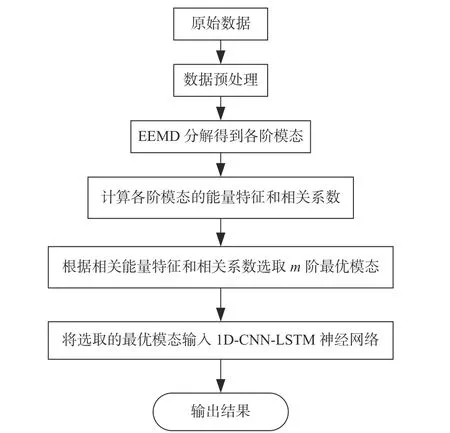
圖1 EEMD-CNN-LSTM高速列車橫向蛇行失穩預測方法

1)獲取數據并進行預處理。

2)使用EEMD算法分解預處理數據，得到固有模態IMF。

3)根據式(1)、(2) 分別提取固有模態的能量特征和計算固有模態的相關系數。

4)根據步驟3）計算得到的相關系數和能量特征的分布規律挑選最優的固有模態。

5)將每個樣本數據的最優固有模態按順序排列為二維矩陣。

6)將步驟5）構造完的矩陣輸入CNN-LSTM神經網絡并輸出結果。

3 實驗驗證與分析

3.1 實驗數據說明

本文所用的實驗數據來源于某高速動車的橫向轉向架實測數據。由于判定高速列車轉向架橫向失穩的條件是轉向架構架橫向加速度信號經過0～ 10 Hz濾波后，其峰值連續6次以上（包括6次）達到或超過8～ 10 m/s2的極限值。因此對原始數據采用0～ 10 Hz低通濾波，并進行250 Hz重采樣預處理，重采樣在保留原始數據的信息條件下去掉不必要的數據點，從而減少計算量。從中挑取100組驗證數據。其變化特征分為4種，分別為蛇行失穩、小幅發散、小幅收斂、正常。樣本數量一共100組，其中60組用于訓練，40組用于測試。

圖2與圖3分別為高速列車構架橫向加速度的小幅蛇行收斂和小幅蛇行發散的演變過程，根據工程經驗，選取樣本的數據輸入長度為300，即采取1.2 s的數據作為模型輸入。

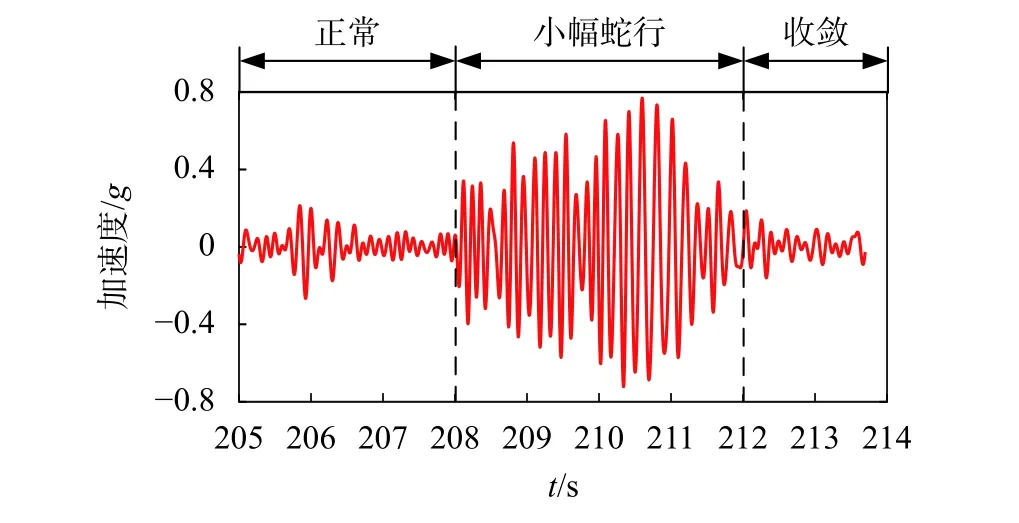
圖2 小幅蛇行收斂演變過程

圖3 小幅蛇行發散演變過程

3.2 實驗的結果與分析

圖4為對100個測試樣本進行EEMD分解后，計算各階模態與原始信號的相關系數，得到分布圖。從圖中可以看出在2，3，4階模態的相關系數較大，但是在2階和4階模態中出現了很多負值，即表現為負相關，這對模態的選擇有較強的干擾。圖5為各階模態能量特征分布圖，其能量主要集中在第3階模態中，而其他模態分布處于相對較低水平。圖6為通過本文提出的各階模態關聯度J分布圖，可以看出，J的較大值（>0.5）集中分布在 2、3、4階模態。其綜合考慮了相關系數與能量特征這兩個因素，能夠較好地選擇出最優模態。

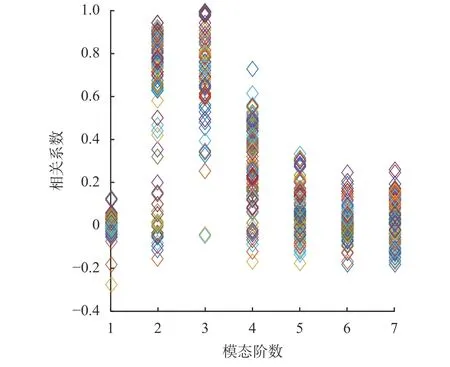
圖4 各階模態相關系數分布圖

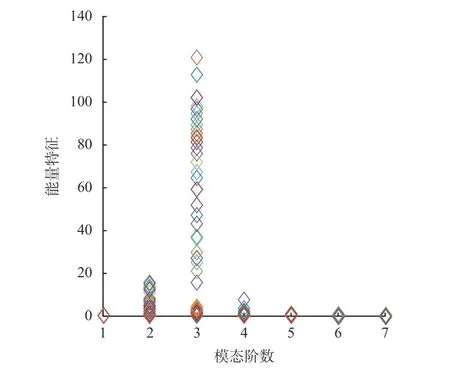
圖5 各階模態能量特征分布圖

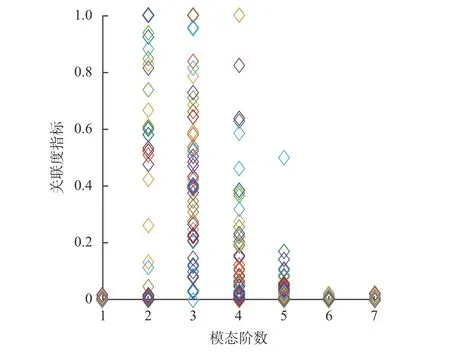
圖6 各階模態關聯度指標J分布圖

圖7為J的最大值統計圖，可以看出J的最大值主要分布在2、3、4階模態中。因此根據圖5，圖6可以得出；本實驗數據經過EEMD分解后，其2、3、4階模態包含原始數據的最主要信息，故將2、3、4階模態作為神經網絡模型的輸入數據。

圖7 指標J的最大值所在模態統計圖

表1為經過調試后的EEMD-CNN-LSTM神經網絡模型的基本結構與具體參數，其輸出維度中的None表示樣本數，即該維度會隨著輸入樣本數的變化而變化，因此無法給出具體值。

表1 EEMD-CNN-LSTM神經網絡結構

表2 為 EEMD-CNN-LSTM 與 CNN-LSTM 和EEMD-SVD-LTSA[12]3種方法的預測結果，可以看出EEMD-CNN-LSTM最優，能夠較好地識別所有變化特征，而CNN-LSTM方法次之，對蛇行收斂的識別能力較差。CNN-LSTM的神經網絡結構與表1結構相同，其主要區別為輸入時沒有對原始信號進行EEMD分解，而是直接將預處理數據輸入模型中。通過這兩種方法的比較結果說明EEMD能夠較好地分離高速列車轉向架橫向加速度信號特征，同時也說明了本文所提出挑選EEMD最優模態算法的有效性。EEMD-SVD-LTSA的識別能力最差，無法準確區分蛇行收斂與蛇行發散特征，說明該方法泛化能力較差，難以適應信號較為復雜的變化規律，這也從側面說明了神經網絡應用在高速列車構架橫向加速度分析的優越性。

表2 預測分類結果 %

表3比較了3種方法的計算速度，其結果為統計20組樣本的計算時間，然后取平均值。通過比較發現，EEMD-CNN-LSTM與CNN-LSTM的計算速度明顯優于EEMD-SVD-LTSA。而CNN-LSTM由于不需要進行EEMD的預處理，因此其計算速度比EEMD-CNN-LSTM更快，但是在本數據集中，其分類效果比EEMD-CNN-LSTM差。因此在滿足計算速度的條件下，EEMD-CNN-LSTM在本數據中的表現優于其他兩種方法。

表3 計算的時間

4 結束語

為了能夠預測高速列車是否會發生橫向蛇行失穩，本文提出EEMD-CNN-LSTM方法，利用該方法分析小幅蛇行的演變趨勢，從而達到預測列車橫向蛇行失穩。根據實驗結果，可以得出以下結論：

1)本文提出的篩選EEMD最優模態方法有效，能夠與CNN-LSTM預測方法相結合。

2)本文提出的EEMD-CNN-LSTM優于CNNLSTM和EEMD-SVD-LTSA，說明了該方法的有效性。