基于遺傳算法管制員崗位排班
張旭





摘要:排班問題是一個重要的組合優化問題[2],每種特定情況下的排班都有各自不同的解決手段。本文在考慮到管制員排班過程中的各種限制條件的情況下提出一種基于排班時長公平性的遺傳算法[4]管制員排班模型。經過實驗改進算法程序能夠在幾分中之內得出一個周期內的具體排班。
一、管制員排班的特點
在民航系統中,管制員是守護安全的第一線人員,由于崗位的特殊性,他的崗位排班與人員的資質直接相關,在現場運行過程中由于人員的資質不相同,相應的個人排班代碼也不盡相同(如領班代碼只能由具有領班資質的人值守)。隨著各種限制要求的增加,人工排班過程中不時會出現顧此失彼的情況,本文綜合上述考慮,從人員搭配,人員資質,平均時長,特定日期代碼需求,上下半夜教員排班五個方面著手建立遺傳算法排班模型。
二、管制員排班模型
2.1 排班限制條件分析
日常排班過程中,首先要考慮的是管制員的資質問題,現有參與排班的管制員資質大致如下:領班,教員,管制員,新放單管制員,部分放單管制員。每種資質所對應的代碼集合都不一樣,在實際排班中用不同的代碼字符表示。人員特定日期的代碼需求可以預先在代碼表中體現出來,此過程體現在預排班中。每類資質人員的排班代碼和人員搭配有不同的要求。本文主要的排班目標為,整體管制員工作小時數最平均,盡量避免連續大夜,滿足上下半夜均有教員,滿足資質搭配要求,滿足個人的輪空需求這五個方面進行排班,求解多目標條件下的極值[3]。
算法模型
其中表示相應的權重系數,fs表示小時數的方差,fn表示連續大夜的罰值函數,fp表示滿足人員代碼需求的罰值函數,fj表示滿足上下半夜教員排班的罰值函數,fm表示人員資質搭配的罰值函數。
其中表示每個人的排班周期內的小時數總數,表示排班的周期內的平均小時數。
其中表示第i為管制員的相鄰兩個代碼,為判斷函數,若果為兩個連續大夜則返回1,否則為0。
其中分別為排班表和特定需求表,為判斷函數,如果ScheduleTable里面特定 位置的與Personneeds中相應位置的相同則返回0,否則返回1。
其中表示教員資格的人數,分別表示第i時段的教員代碼集合,上半夜代碼集合,下半夜代碼集合。為判斷函數,如果Gi中的代碼既在patternS里面又在patternX里面則表示上下半夜都有教員,則返回1,否則返回0。
其中分別表示不能搭配的人員的代碼對集合和排班代碼中相互搭配的代碼對集合。為判斷函數,如果在中則返回1,否則為返回0。
對于遺傳算法函數的松弛函數的確定,通過
綜上所述:整體基于遺傳算法的管制員排班模型為下:
2.2 算法復雜性分析
根據排列組合原理計算可以得到,N位排班人員在T周期之內排班的解空間大小為,從中可以看出隨著排班周期和人數的增加解空間的大小呈指數增加,傳統的算法很難在有限的時間內求得滿意解,因此選擇啟發式算法。根據遺傳算法的特點,本文針對管制員算法的特定,設計了相關的遺傳算法。算法能夠在5分中之內求得滿足條件的滿意解,大大減少了排班的人力成本 。通過跟現場的各個小組的排班人員的調查分析了解到。正常情況下制訂一個有特定需求的排班,平均需要花費1~2小時,有時候甚至需要更長的時間。并且由于口算的局限性,很難保證同時滿足多個限制條件。
2.3 遺傳算法設計
考慮到排班過程中,每天的代碼都是相同的,所以每個在產生初始種群的過程中,我們根據實際的排班要求隨機產生每天的排班,也就是排班表中的一列的數據(遺傳基因),然后通過循環來產生一個周期內的排班表(染色體)。在常規的遺傳算法的運算過程中,交叉操作是為了產生新的優良的個體,變異操作是為了防止算法過早的陷入局部最優解。一旦在初始種群確定之后,整個種群的基因就基本上是確定的了,交叉操作并不能保證整個搜索的遍歷性,因此本文中,變異也作為產生新個體的一個重要的手段,因此在本文中設置的變異概率要遠遠大于常規遺傳算法的變異概率。
產生初始種群,本文將每一個可能的排班表作為一個遺傳父本。
其中表示第i個人第j時段的代碼。
關于遺傳算法的設計的基礎知識在[1]已經有較為詳細的描述,本文采用類似的遺傳算法編碼方法。本文直接將每個排班表作為父本,進行算法操作。算法交叉操作
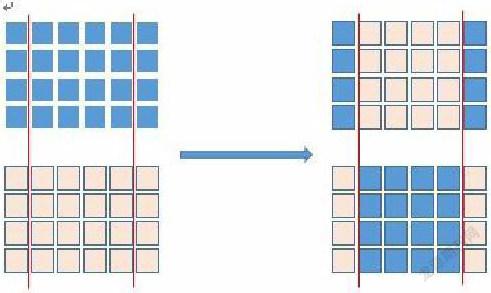
本文采用兩點交叉法。為了能夠使得遺傳向著較好的方向進行,更快地逼近最優解。在算法運算過程中再加入一些特殊的點交叉具體過程如下圖
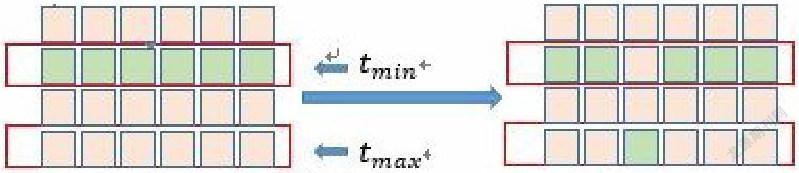
變異過程示意圖:
算法分析:
根據每個系數的設置我們可以看出適應度函數值的跨度比較大。從1000~10。這樣在遺傳算法的執行過程中,很可能會使得函數過早地陷入局部最優解。因此在算法在執行過程中有很大的可能性較早的陷入局部最優解。因此,本文在算法執行過程中設置了一個操縱算法——偽變異過程。在計算過程中將小時數最多的人的一個大夜代碼與小時數最少的對應位置的代碼互換。如圖所示
為了能夠較好地,較全面地搜索到最優解,設置變異地概率在50%以上。
算法檢驗
在本算法設計過程中,產生新的遺傳個體的產生并不是主要通過交叉過程獲得,而是通過隨機的變異過程來獲得。因此實驗中變異的概率要設置在50%以上,才能很好的保證算法的遍歷性。
上圖是一個預排班表,列表示排班周期為9,排班人數為13人。字符O表示人員的代碼需求,實際排班中表示輪空代碼,不能搭配人員序號組合為[9 13;7 13]。右側為算法排班結果,本次實驗用時178秒。
三、分析與展望
雖然本文針對具體的管制員排班進行分析,但是文中所提到的編碼手段對于此類排班都是有效的,通過適當方式的編程方式能夠實現在一分鐘之內就能得到較滿意的解。罰值函數的確定和罰值函數系數的確定是遺傳算法能否有效搜索的重要條件。文中所給出的系數都是通過參考罰值函數的值,然后預估一個較合適的系數,再通過多次試驗不斷改進得出的,并沒有確定罰值函數系數的計算公式,這是在未來研究的一個方向,如果能夠確定準確的罰值函數系數組合,那么算法的收斂速度和搜索的精度就會大大的提高,排班結果也會更好。
參考文獻:
[1] 武廣號, 文毅, 樂美峰. 遺傳算法及其應用[J]. 應用力學學報, 2000, 23(6):9-10.
[2] 孫宏. "航空公司飛機排班問題:模型及算法研究." 西南交通大學, 2003.
[3] 胡毓達. 實用多目標最優化[M]. 上海科學技術出版社, 1990.
[4] https://baike.baidu.com/item/%E9%81%97%E4%BC%A0%E7%AE%97%E6%B3
(民航局運行監控中心 北京 100010)

