雙高箱雙層集裝箱運輸體系弓網動力學性能研究

呂青松

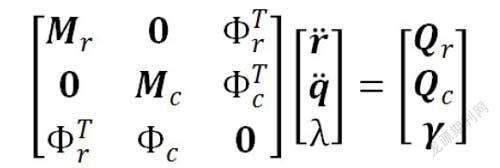
摘 要：鐵路機車車輛運行時，弓網系統的受流質量主要受到弓網系統動力學影響。雙高箱雙層集裝箱運輸體系下的接觸網高度超過了現有國內接觸網導線高度的最大值，以雙高箱雙層集裝箱運輸體系的試驗線金甬鐵路為例，接觸網導線高度為6 685 mm。為了研究受電弓與在滿足雙高箱雙層集裝箱運輸體系下的接觸網的動力學相互作用關系，結合弓網耦合動力學分析了和諧電力機車和CRH2型車兩種工況下弓網動力學性能。結果表明：機車受電弓和動車受電弓在接觸導線高度為6 685 mm下，接觸壓力最小值和統計最小值均大于零，但隨著速度的提高（從160 km/h提高至200 km/h）弓網受流質量開始惡化，標準差增大，統計最小值均小于20 N，但并未出現失壓狀況，弓網系統動力學和受流質量總體上滿足條件要求。

關鍵詞：受電弓;接觸網;受流質量;弓網系統動力學

0 引言

近年來，我國經濟發展進入新時代，全社會對鐵路集裝箱運輸潛在需求很大，加之國家出臺一系列政策鼓勵促進包括集裝箱和多式聯運在內的快速發展，目前我國已將高速鐵路、重載鐵路、雙高箱集裝箱運輸作為交通強國鐵路先行的重要支撐點，從戰略高度上將雙高箱集裝箱運輸作為打造一帶一路，陸港通道，江海聯運的重要品牌。因此，開展雙高箱集裝箱運輸體系研究，為我國鐵路雙高箱集裝箱運輸提供可借鑒的成果并積累可推廣的經驗具用重要意義。

列車運行過程中所需能量通過接觸網與受電弓系統傳輸。通過列車上的受電弓滑板與鐵路線路上的接觸線的滑動接觸實現接觸網向列車的能量傳輸。從目前我國現有的技術標準和國內既有鐵路接觸網導線高度上來說，接觸網最大高度均沒有高于6 500 mm。以金甬鐵路為例，接觸網導線高度達到了6 685 mm。目前，國內外對于接觸網導線為6 685 mm條件下的弓網動力學性能和弓網受流質量均無研究，因此，開展雙高箱雙層集裝箱運輸體系弓網動力學性能研究，為我國鐵路雙高箱集裝箱運輸提供必要的技術支持是十分必要的。

本文主要針對電力機車和動車組上的受電弓與滿足雙高箱雙層集裝箱運輸體系的接觸網取流時，研究影響弓網動力學性能的因素。分析電力機車和動車組兩種模式下的受電弓與接觸網的動力學性能，以及對弓網受流性能的影響，為鐵路雙高箱集裝箱運輸體系提供基礎數據和參考依據。

1 弓網系統動力學模型

1.1 接觸網模型

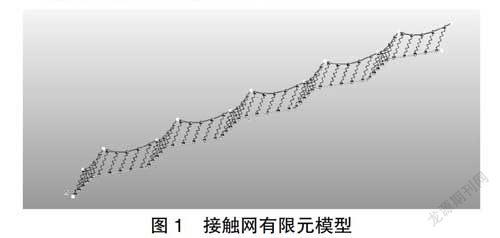
接觸網模型采用有限單元法進行直接建模，接觸網采用簡單鏈型懸掛形式，通過定義接觸網各部件在空間的幾何位置及拓撲關系，得到其幾何模型，接觸線和承力索采用梁單元進行模擬，吊弦在實際工作環境中，傳遞的壓縮力非常小，通常采用只受拉不受壓的非線性彈簧單元來模擬。最后，通過對接觸網的有限元劃分，從而建立接觸網的有限元模型，再通過有限元組裝技術，得到系統的質量陣M，阻尼陣C，剛度陣K以及外載荷列陣F，從而建立接觸網的運動微分方程：

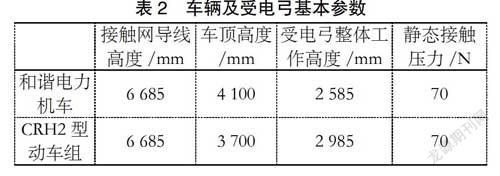
本文基于金甬鐵路接觸網系統的結構及參數，見表1，接觸網導線高度為6 685 mm，接觸網結構高度為：1 400 mm，通過在ANSYS-APDL中編制接觸網有限元模型，進行單元劃分，通過ANSYS的靜態計算器，得到接觸網的靜態構型。

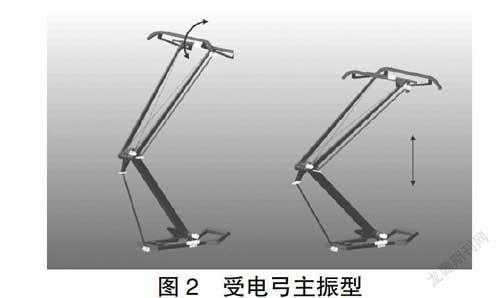
1.2 受電弓模型

進行弓網耦合動力學仿真時，受電弓模型通常可采用集中質量模型、多剛體模型以及剛柔混合模型等。本文采用多剛體模型進行研究，多體動力學計算軟件Recurdyn基于相對坐標法開發，對于多剛體系統的計算具有計算效率和精度的優勢，本文將采用Recurdyn進行受電弓多剛體建模。

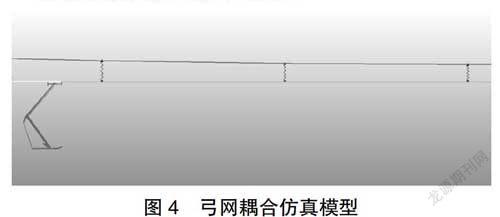
1.3 弓網耦合模型

對于弓網接觸問題，通常采用罰函數法進行模擬，采用線性彈簧模擬弓網間的接觸剛度，受電弓與接觸網之間通過接觸壓力耦合在一起，將受電弓與接觸網的動力學方程組合在一起，構成弓網耦合系統動力學方程：

2 弓網系統動力學分析

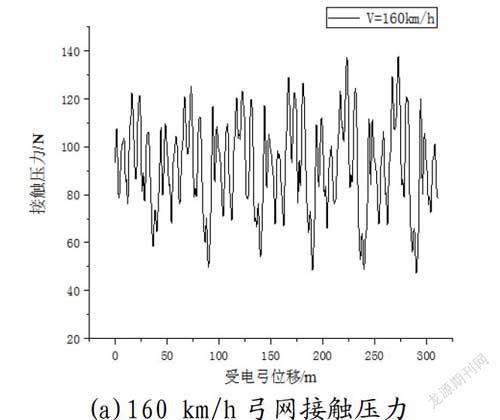
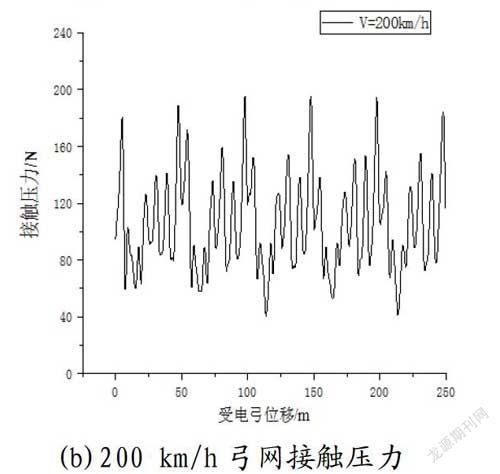
文中主要針對CRH2型動車組及和諧電力機車上的受電弓與滿足雙高箱雙層集裝箱運輸體系下的接觸網（接觸網導線高度6 685 mm）受流時的弓網耦合動力學進行分析，CRH2型動車組上的受電弓工作高度為2 985 mm，和諧電力機車上的受電弓工作高度為2 585 mm。

本文研究了CRH2型動車組分別在160 km/h、200 km/h

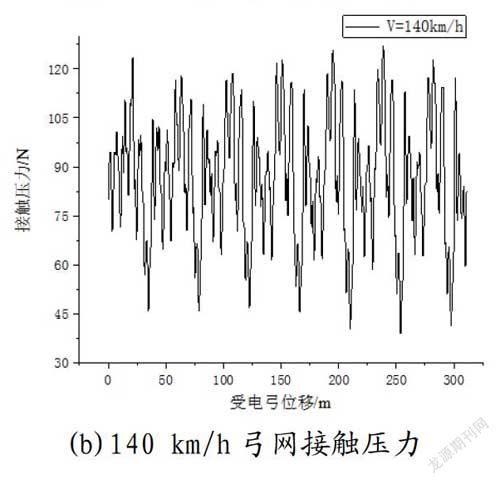
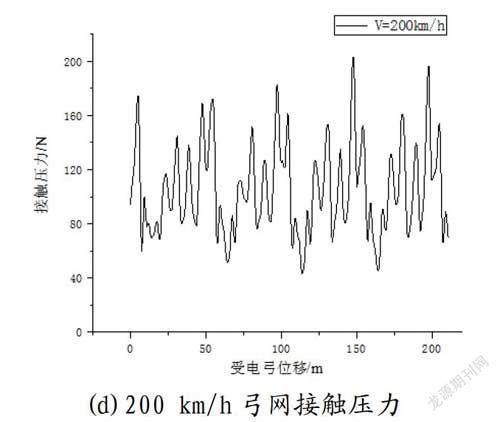
兩個不同速度等級下、和諧電力機車分別在120 km/h、140 km/h、160 km/h、200 km/h四個不同速度等級下的動力學性能。

2.1 CRH2型動車組仿真研究結果

2.2 和諧電力機車仿真研究結果

2.3 接觸壓力統計值

對仿真工況下的接觸壓力進行統計，得到如表3弓網受流性能對比統計指標：

2.4 結語

從弓網耦合系統動力學計算機仿真技術研究角度分析，機車受電弓和動車受電弓在滿足雙高箱雙層集裝箱運輸體系下的接觸導線高度（6 685 mm），接觸壓力最小值和統計最小值均大于零，變異系數均大于1/3，并未出現失壓狀況，弓網系統動力學和受流質量總體上滿足條件要求。但隨著速度的提高（從160提高至200）弓網受流質量開始惡化，標準差增大。

參考文獻：

[1]T.X.WU，M.J.BRENNAN.Basic Analytical Study of Pantograph-catenary System Dynamics[J].Vehicle System Dynamics：International Journal of Vehicle Mechanical and Mobility，1998（30）：443-456.

[2]李豐良，李敏，唐建湘.受電弓的建模與參數測試[J]. 中南大學學報，2006，37（1）：194-199.

[3]梅桂明，張衛華.受電弓/接觸網系統動力學模型及特性[J].交通運輸工程學報，2002，2（1）：20-25.

[4]周寧，李瑞平，張衛華.基于負弛度法的接觸網建模與仿真[J].交通運輸工程學報，2009，9（4）：28-32.

[5]張衛華，沈志云.受電弓動力學研究[J].鐵道學報，1993，

15（1）：23-30.

[6]ZHANG W H，MEI G M，WU X J and CHEN L Q.A study on dynamic behaviour of pantographs by using Hybrid simulation method[J].Rail and Rapid Transit，2005， 219（3）：189-199.

[7]周寧，張衛華.基于受電弓彈性體模型的弓網動力學分析[J].鐵道學報，2009，31（6）：26-32.

[8]Ning ZHOU，Wei-hua ZHANG，Rui-ping LI.Dynamic performance of a pantograph-catenary system with the consideration of the appearance characteristics of contact surfaces[J].Journal of Zhejiang University-SCIENCE A （Applied Physics & Engineering），2011，12（12）：913-920.