梁拱組合體系橋梁自振頻率參數敏感性分析

袁霖宇

（廣東省交通規劃設計研究院集團股份有限公司，廣東 廣州 510507）

橋梁結構的振動特性反映結構整體的固有特性[1～3]，是進行橋梁結構振動控制，抗震、抗風設計及預測復雜動力荷載作用下結構動力響應的基礎。由于施工的不可預知性、材料加工的不確定性以及模型簡化等因素，僅按設計圖紙建立橋梁結構有限元模型并不能真實反映結構的受力狀態，導致計算得到的結構動力特性不準確。大跨度鋼箱拱橋是山區、跨河及景觀要求較高的地區最為常見的一種橋型，上飛燕式梁拱組合橋梁[4～5]作為一種新型的鋼箱系桿拱橋，結構體系復雜，有必要了解橋梁各結構參數對結構自振頻率和固有頻率的影響，為后續設計及管養提供參考。

本文以某上飛燕式梁拱組合橋為研究對象，采用有限元類比的方法，從彈性模量、構件的質量密度、吊桿的索力誤差等方面進行動力特性的參數敏感性[6～7]分析，全面綜合研究該體系橋梁結構動力特性與各因素之間的關系。

1 工程概況

某上飛燕式梁拱組合橋總體跨徑布置為40 m+120 m+40 m，橋梁標準橫斷面寬30.5 m；拱圈為矩形鋼箱斷面結構，拱軸線為二次拋物線形，橋梁矢跨比1∶4，橋面吊桿間距6 m，共設置16對吊桿；風撐結構為“X”形。橋梁從立面上看為上飛燕式造型，從橫斷面上看為門式造型。見圖1和圖2。

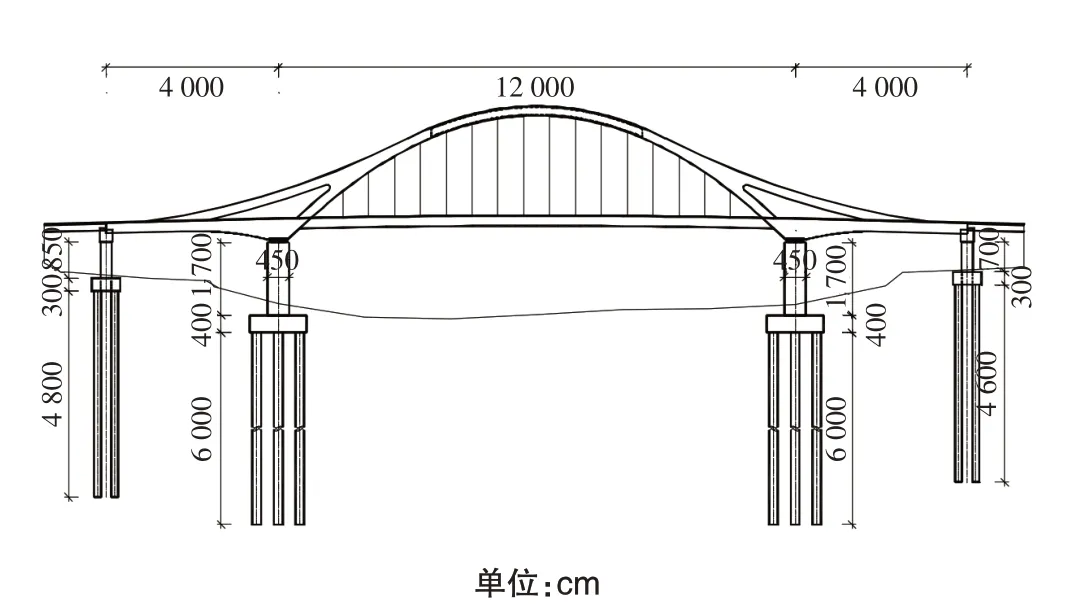
圖1 橋梁總體布置

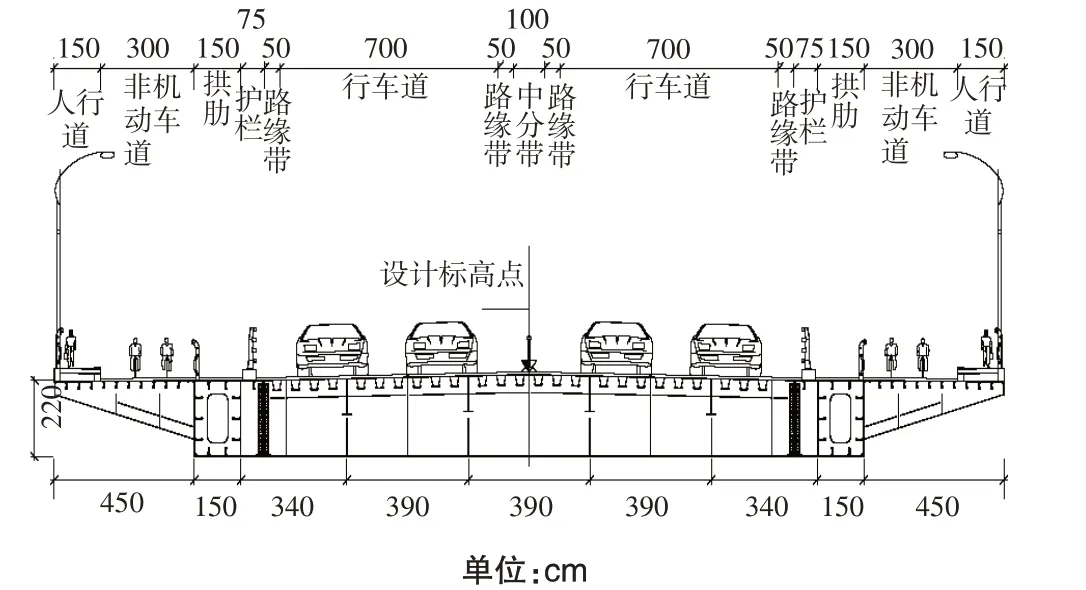
圖2 標準橫斷面

2 模型的建立

采用MIDAS Civil軟件建立全橋有限元模型，劃分1 568個單元、1 353個節點，其中鋼箱梁、鋼拱圈、風撐等均采用梁單元模擬，吊桿采用桁架單元模擬；橋面約束體系按實際支座位置進行布置并耦合相應自由度。模型中結構自重、二期恒載等均按實際質量分布進行模擬；車道及人群荷載按JTGD 60—2015《公路橋涵設計通用規范》進行施加；結構整體升溫30℃，整體降溫-25℃，同時考慮溫度梯度影響。見圖3。

圖3 橋梁結構有限元模型

3 動力特性分析

采用子空間迭代法進行分析[8～9]，見表1和見圖4。

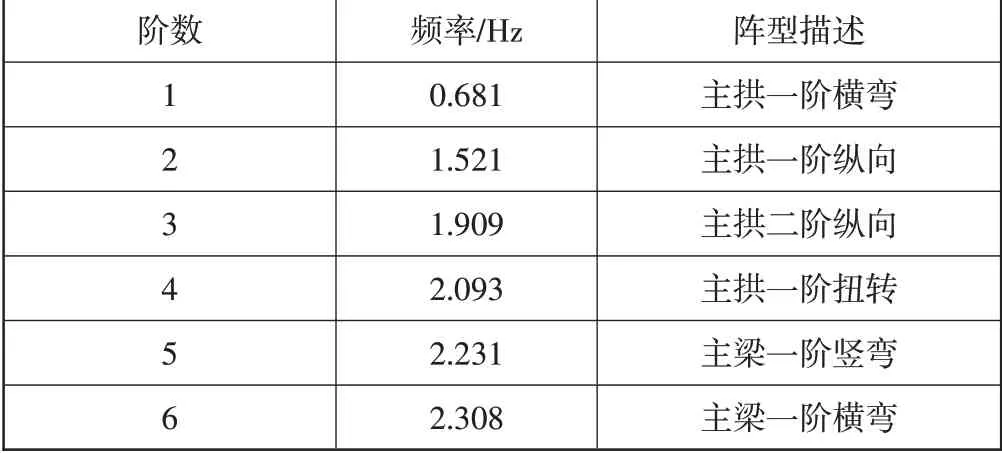
表1 自振頻率及陣型

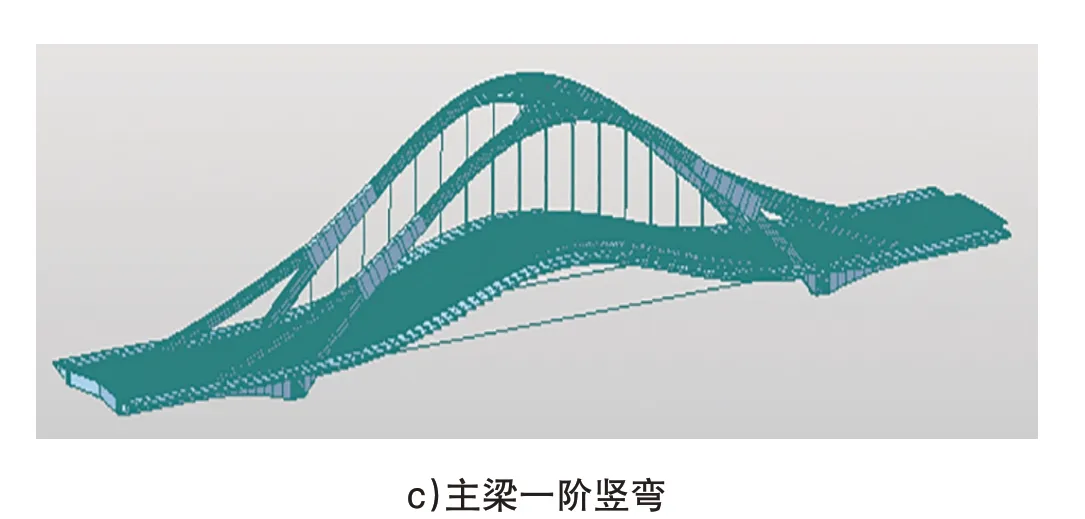
圖4 橋梁主要陣型

1）橋梁一階頻率為0.681 Hz，陣型為主拱橫向彎曲，充分體現了梁拱組合體系橋梁柔性特征，與常規的拱橋特點一致。

2）橋梁陣型排列依次為主拱一階橫彎、主拱一階縱彎、主梁一階豎彎、主梁一階橫彎，各陣型排列合理；各階頻率相差較大，之間不易出現耦合振動。

3）第一階陣型為拱圈橫向彎曲，與該橋僅在拱圈頂部設置風撐有較大關系，同時第一階頻率為0.681 Hz，與第二階陣型頻率差別較大，表明該橋拱圈橫向剛度較弱，需加強風撐設計及穩定性驗算。

4 結構參數敏感性

敏感性是評估結構動力特性受結構影響程度的一種手段，已成為當下的研究熱點。該上飛燕類型橋梁是典型的三元結構，活載分布的構件為主梁、橫梁和橋面板，力的傳遞構件是吊桿，而重要的承重構件是拱肋和主梁。

眾所周知，結構的動力特性與結構的質量密度及彈性模量有較大關系。主拱和主梁的彈性模量和質量密度在該體系橋梁整體動力特性中占有重要地位，由于構件制造的尺寸誤差、施工的不確定性等因素，主梁的實際質量會與設計圖紙的質量有誤差，同時吊桿施工過程中索力也會有一定的誤差，因此，有必要研究該體系橋梁彈性模量、質量密度、吊桿張拉力對結構固有頻率的敏感性。

4.1 彈性模量

主梁及主拱彈性模量按0.5、0.75、1.00、1.25、1.25倍數進行變化。隨著主梁彈性模量的增加，一階頻率幾乎沒有變化；二階頻率從1.101 Hz變化至1.830 Hz，增加了66.2%；三階頻率從1.483 Hz變化至2.228 Hz，增加了50.2%；四階頻率從1.645 Hz變化至2.365 Hz，增加了43.7%；五階頻率從1.721 Hz變化至2.396 Hz，增加了39.2%；六階頻率從1.929 Hz變化至2.799 Hz，增加了45.1%。隨著主拱彈性模量的增加，二階、六階頻率幾乎沒有變化；一階頻率從0.487 Hz變化至0.824 Hz，增加了69.1%；三階頻率從1.777 Hz變化至2.200 Hz，增加了23.8%；四階頻率從1.823 Hz變化至2.227 Hz，增加了22.2%；五階頻率從1.981 Hz變化至2.322 Hz，增加了17.2%。見圖5。

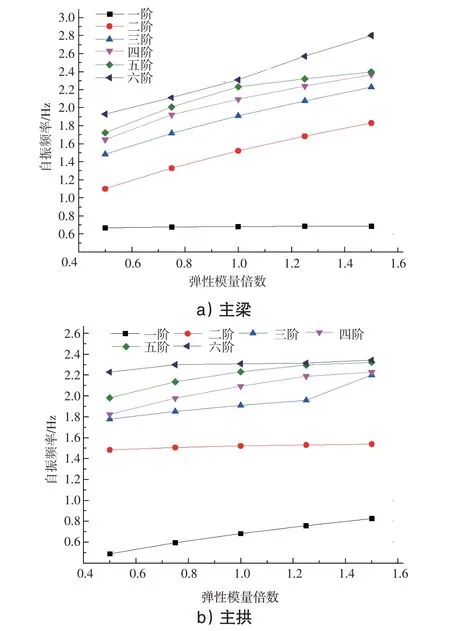
圖5 彈性模量對自振頻率的影響

彈性模量能顯著改變上飛燕式梁拱組合橋的自振頻率，隨著彈性模量增加，相應的頻率增加且主梁彈性模量影響程度要比主拱彈性模量要大。

4.2 質量密度

主梁及主拱質量密度按0.5、0.75、1.00、1.25、1.25倍數進行變化。隨著主梁質量密度的增加，一階頻率幾乎沒有變化；二階頻率從2.022 Hz變化至1.244 Hz，減少了38.4%；三階頻率從2.343 Hz變化至1.611 Hz，減少了31.2%；四階頻率從2.452 Hz變化至1.836 Hz，減少了25.1%；五階頻率從2.957 Hz變化至1.861 Hz，減少了37.1%；六階頻率從3.114 Hz變化至1.884 Hz，減少了39.4%。隨著主拱質量密度的增加，二階、五階、六階頻率幾乎沒有變化；一階頻率從0.947 Hz變化至0.551 Hz，減少了41.8%；三階頻率從2.028 Hz變化至1.811 Hz，減少了10.7%；四階頻率從2.284 Hz變化至1.836 Hz，減少了19.6%。見圖6。

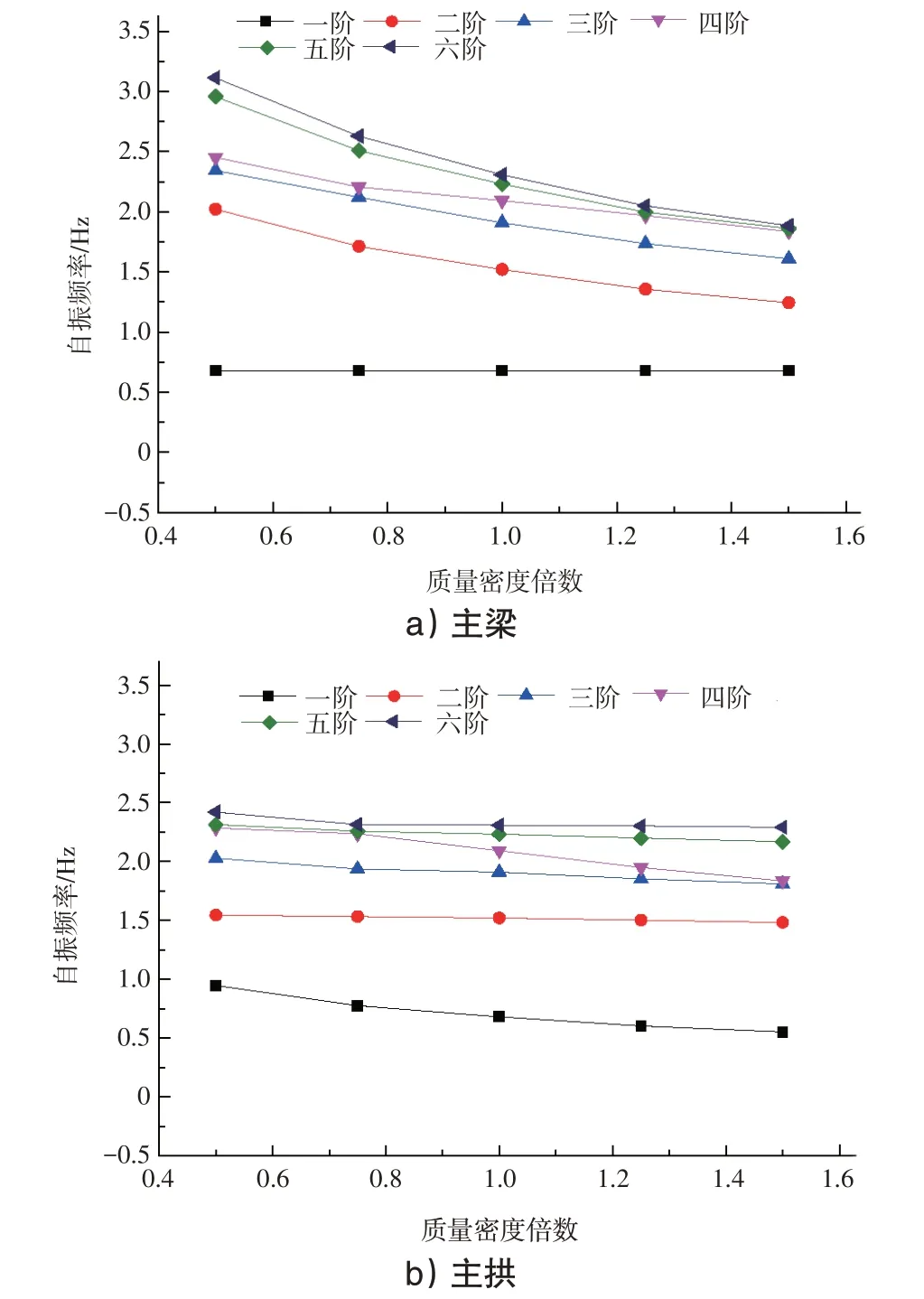
圖6 質量密度對自振頻率的影響

質量密度能顯著改變上飛燕式梁拱組合橋梁的自振頻率，隨著質量密度的增加，相應的頻率減小且主梁質量密度影響程度要比主拱質量密度要大。

4.3 吊桿力誤差

吊桿力按0.95、1.00、1.05倍數進行變化。吊桿力對橋梁自振頻率幾乎沒有影響，設計中可忽略吊桿力的影響。見圖7。

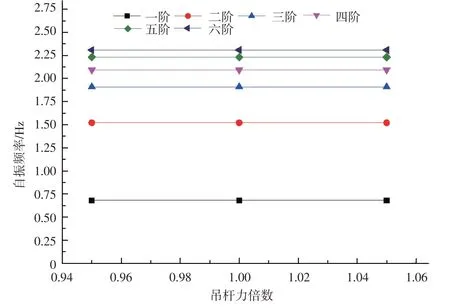
圖7 吊桿力倍數對自振頻率的影響

5 結論

1）上飛燕式梁拱組合體系橋梁陣型排列依次為主拱一階橫彎、主拱一階縱向彎曲、主梁一階豎彎、主梁一階橫彎，各陣型排列合理，各頻率之間相差較大，不易出現耦合振動。

2）彈性模量能顯著改變上飛燕式梁拱組合橋的自振頻率，隨著彈性模量增加，相應的頻率增加且主梁彈性模量影響程度要比主拱彈性模量要大。

3）質量密度能顯著改變上飛燕式梁拱組合橋的自振頻率，隨著質量密度的增加，相應的頻率減小且主梁質量密度影響程度要比主拱質量密度要大。

4）吊桿力對自振頻率幾乎沒有影響，設計中可忽略吊桿力對自振頻率的影響。