非線性分類模型在高速公路邊坡監測中的應用

陶 虎

(廣西交投科技有限公司，廣西 南寧 530000)

0 引言

高速公路邊坡是破壞主體自然結構并對其進行防護形成的人造結構，沿線邊坡極易受到地質條件和環境因素的影響而失穩，造成滑坡、塌方、落石等災害，對沿線公路造成巨大的破壞，對通行車輛和人員的安全造成嚴重威脅。因此在高速公路邊坡監測中，如何準確有效預測邊坡形變發生，掌握邊坡的地質變化和發展趨勢，是高速公路養護管理部門在災害發生前提前做好邊坡防護防治、交通警示疏導等措施，減少人員財產經濟損失的關鍵。

高速公路邊坡監測的實際目的是進行邊坡形變預測，對邊坡形變后期的發展做出及時、準確的預判[1]。邊坡的形變發展是從蠕動、快速滑動到滑坡的過程，此過程中一些可監測的地質參數(例如邊坡位移量、地聲、應力、地下水量位等)也會隨之變化。地質參數變化受多重因素影響，存在非線性和不確定性，如何利用地質參數進行有效、準確的邊坡形變計算預測是非常必要的。

目前，邊坡形變計算預測方法主要有兩類[2]：(1)定性分析法，通過綜合參考邊坡周邊的各種影響因素，及時評判邊坡形變趨勢，分析預測其發展變化，典型的方法有工程地質條件比對法和地質參數因子分析法；(2)定量分析法，對地質形變參數采用數學統計、模糊綜合評判模型或非線性分類模型等方法進行計算，以獲得形變趨勢預測數據。目前邊坡形變預測沒有存在普適性的方法。依據邊坡的地質條件和氣候環境，建立合適的邊坡形變計算預測模型對邊坡形變進行有效預測，是邊坡監測工作的關鍵內容。

本文針對廣西地區特有的地質條件和氣候環境，依托泉南高速公路柳州至南寧段監測項目，應用具備分析非線性和不確定性分類問題的模糊神經網絡模型和支持向量機算法對邊坡地質參數進行計算，獲取地質參數與邊坡形變安全系數的擬合回歸函數，以獲得邊坡形變安全系數的變化趨勢，判斷邊坡安全性，為邊坡防護防治提供科學依據。

1 非線性分類算法模型

1.1 支持向量機算法模型

支持向量機(support vector machines，SVM)是基于VC維理論[3-4]和追求結構化風險最小原理[5]逐步發展而來的機器學習算法。在統計樣本量較少的前提下，能夠獲得十分出色的統計規律模型[6]。在非線性分類模型中分類問題，假設樣本集：(Xi，yi)(i=1，2，3，…，N，y∈{-1，1})，X∈Rn，其中參數y確定正負樣本子集X+、X-，能將樣本由原始的低維度空間映射到高維度空間，使樣本集在維度特征空間具有線性可分的特征。SVM的數學模型中希望得出一個擬合函數f(x)使其分類樣本盡可能接近真實情況。這個模型中以f(x)為中心構造一個距離為γ間隔的分類平面，如圖1所示。

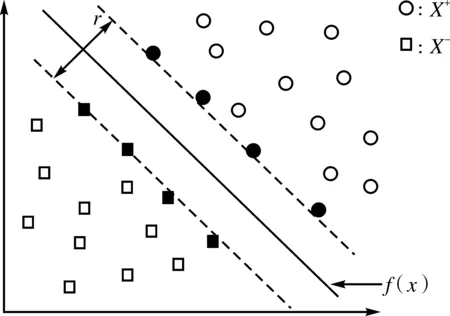
圖1 最優分類超平面示意圖

設一個變量w*和一個常量c*，則約束式擬合函數可寫成判別函數形式：

(1)

其中式(1)向量w*具有最小范數：

(2)

引入松弛變量(ξi，ξi*)，優化判別目標公式為：

(3)

(4)

引入Lagrange乘子法求解二次規劃問題，Lagrange方程式為：

(5)

根據目標函數的約束條件可以得到支持向量機的擬合函數為：

(6)

為了將非線性分類通過特征空間映射到高維度特征空間中進行線性問題求解，因此引入了核函數K(Xi，Xj)代替線性問題中的內積運算：

(7)

1.2 模糊神經網絡模型

模糊神經網絡(FuzzyNeuralNetwork，FNN)模型是綜合了模糊系統和神經網絡的互補優勢性，使該模型具有自主學習、自動識別、自適應模糊化處理等優勢。該模型主要思想為對神經網絡輸入信號模糊化處理，將其轉化為模糊系統的輸入信號和權值。在FNN模型中，實現學習和優化權值系數是算法的關鍵。而基于網絡自適應模糊神經系統(AdaptiveNetwork-basedFuzzyInferenceSystem，ANFIS)則融合了神經網絡學習算法和模糊系統的推理優勢，其原理是給定輸入/輸出的數據集，構造出模糊網絡模型(支持T-S型系統)[7]，利用最小二乘法和單獨反向傳播對系統隸屬函數的參數進行調節。ANFIS模型網絡結構主要有輸入/輸出的變量和空間劃分，判斷規則條數和隸屬度函數個數等部分，它可以對模型的可調整參數進行調整，以此來得到最佳輸出[10]。模糊神經網絡的典型結構如圖2所示。

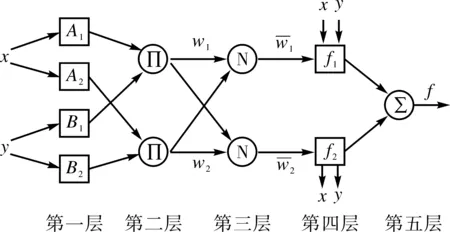
圖2 模糊神經網絡結構圖

在構造模糊網絡模型過程中，將原有模型轉化為自適應網絡模型，從而建立T-S型系統的模糊學習過程。自適應網絡模型為多層的前饋網絡結構。網絡的輸入層主要是將輸入信號模糊化，該層為輸入變量的隸屬函數層，節點i的輸出函數為：

(8)

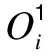
嘉善田歌是民歌藝術的一種特殊表現形式，歸屬于口傳類非物質文化遺產。它們都是口口相傳，并沒有物質性和符號性載體，跟隨著傳承者生而生亡而亡。因此，保護傳承者，對此類非物質文化遺產的保護傳承就顯得尤為重要了。傳承者，即繼承、操縱和創作嘉善田歌的歌手和民間藝人等，是傳承主體的核心。而傳播者和接受者可以被定義成傳播嘉善田歌音樂文化的社會個體或群體，它們可能是一個人，也有可以是一個組織團體，如文化企業、公益社團、媒體和政府等。

首層主要是把模型訓練的評價質變數據傳播到下一層[8]。第二層是對上層傳遞的信號進行乘積運算，結果輸出得到每條規則的適用度，可表達為：

(9)

式中：每個節點i的輸出代表第i條規則的可信度。

第三層是對每條規則的適用度歸一化處理，第i個節點計算第i條規則的ωi占全部規則ω之和的比值為：

(10)

第四層是計算模糊規則輸出，每個節點i均為自適應節點，其輸出結果為：

(11)

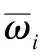
第五層是固定節點，是匯總所有輸入信息計算總輸出：

(12)

ANFIS的輸出結果可在確定前件參數基礎上使用后件參數的線性組合表示[12]：

(13)

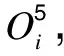
2 監測數據

高速公路邊坡地質穩定性的影響因素多樣，但在實際邊坡監測中邊坡形態的不穩定性發展主要是由內摩擦角φ、重度參數γ、粘聚力c、邊坡角度α、邊坡滑動面與坡面高度H、空隙水壓力ρ等邊坡截面結構因素共同作用造成的[9]。因此本文選取主要影響邊坡地質穩定性因子的實時監測數據，應用非線性分類模型算法計算各參數與邊坡形變安全系數A的擬合回歸函數，獲得A的變化趨勢，來判斷邊坡的安全性。高速公路上常見的邊坡截面結構如圖3所示。

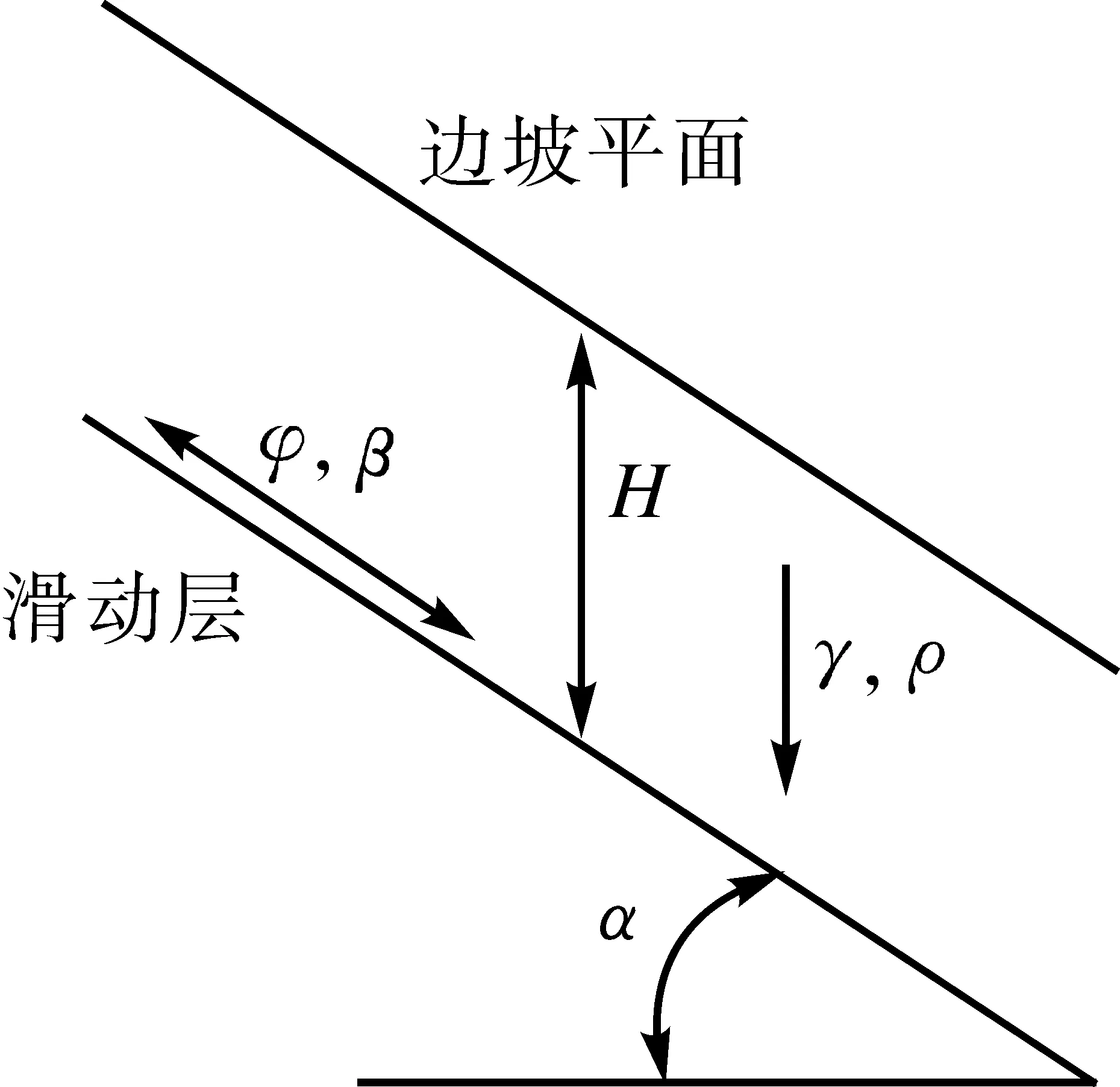
圖3 邊坡截面結構模型示意圖

預測模型的性能與訓練樣本密切相關，訓練樣本需考慮樣本長度與全面性。它們直接影響著模型學習速度、仿真能力以及能否全面反映監測參數與A的因果關系。A劃分為3個等級即穩定、變形、滑坡，并分別賦予值A∈(1，2，3)。本文選取的樣本為泉南高速公路柳州至南寧段共5個邊坡監測點獲得數據40組。其中訓練樣本數據30組(穩定20組，變形5組，滑坡5組)，測試樣本數據10組(如表1所示)。

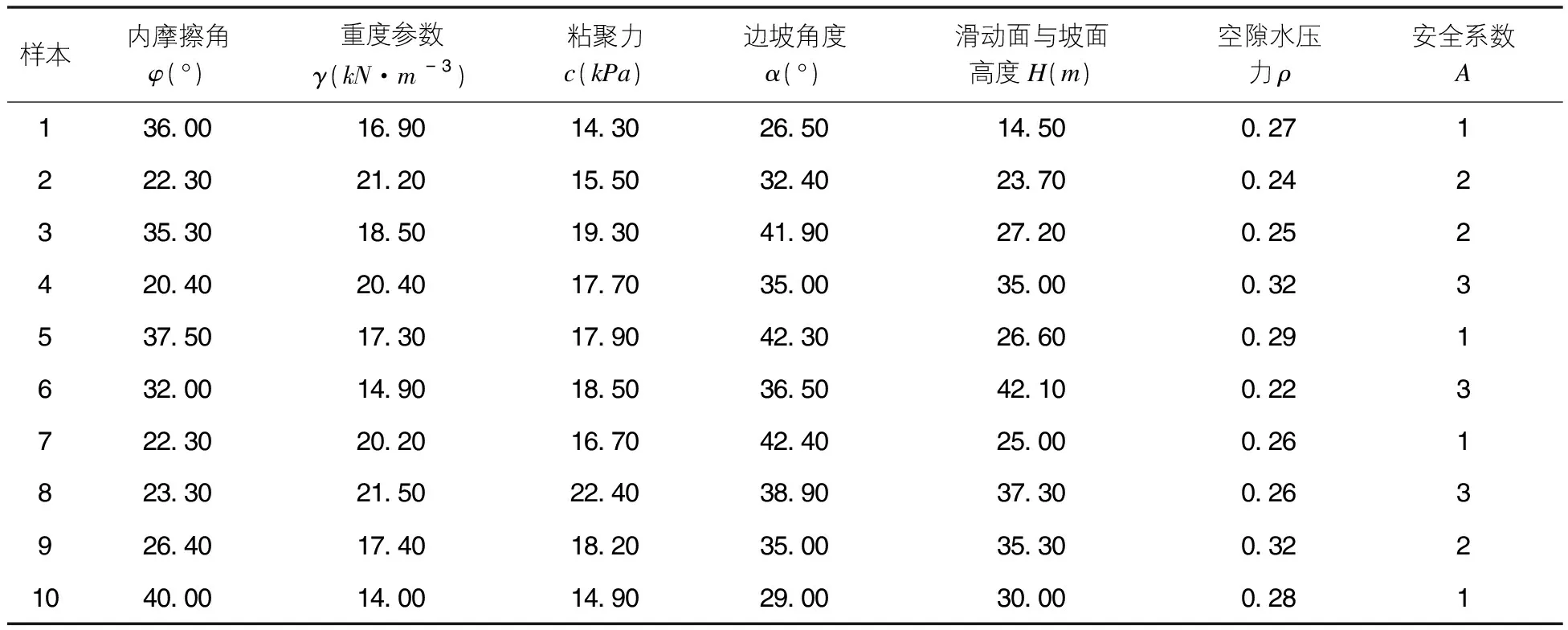
表1 模型測試樣本表

因樣本組存在奇異性，所以對樣本數據進行歸一化處理，公式如式(14)所示：

y=(ymax-ymin)·(x-ymin)/(xmax-xmin)+ymin

(14)

3 模型分類測試結果分析

本文使用MATLAB軟件中的SVM和ANFIS工具包對邊坡監測數據樣本進行模擬測試。SVM模型的核函數選擇更適合分析復雜非線性分類模型的高斯徑向基核函數[7]，該核函數的核半徑為1。ANFIS模型分類器采用了6個輸入節點、1個輸出節點，動量因子選擇為0.5，學習效率為0.1，訓練模型具有良好的誤差收斂性能。使用兩種模型對10組數據進行計算預測得到安全系數結果如表2所示，測試結果誤差比對如圖4所示。

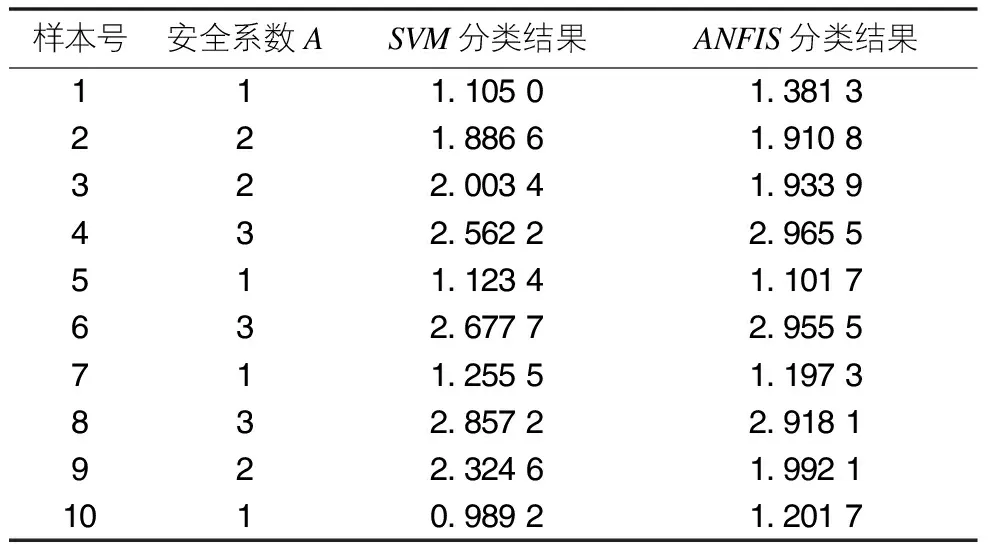
表2 模型分類測試結果比對表

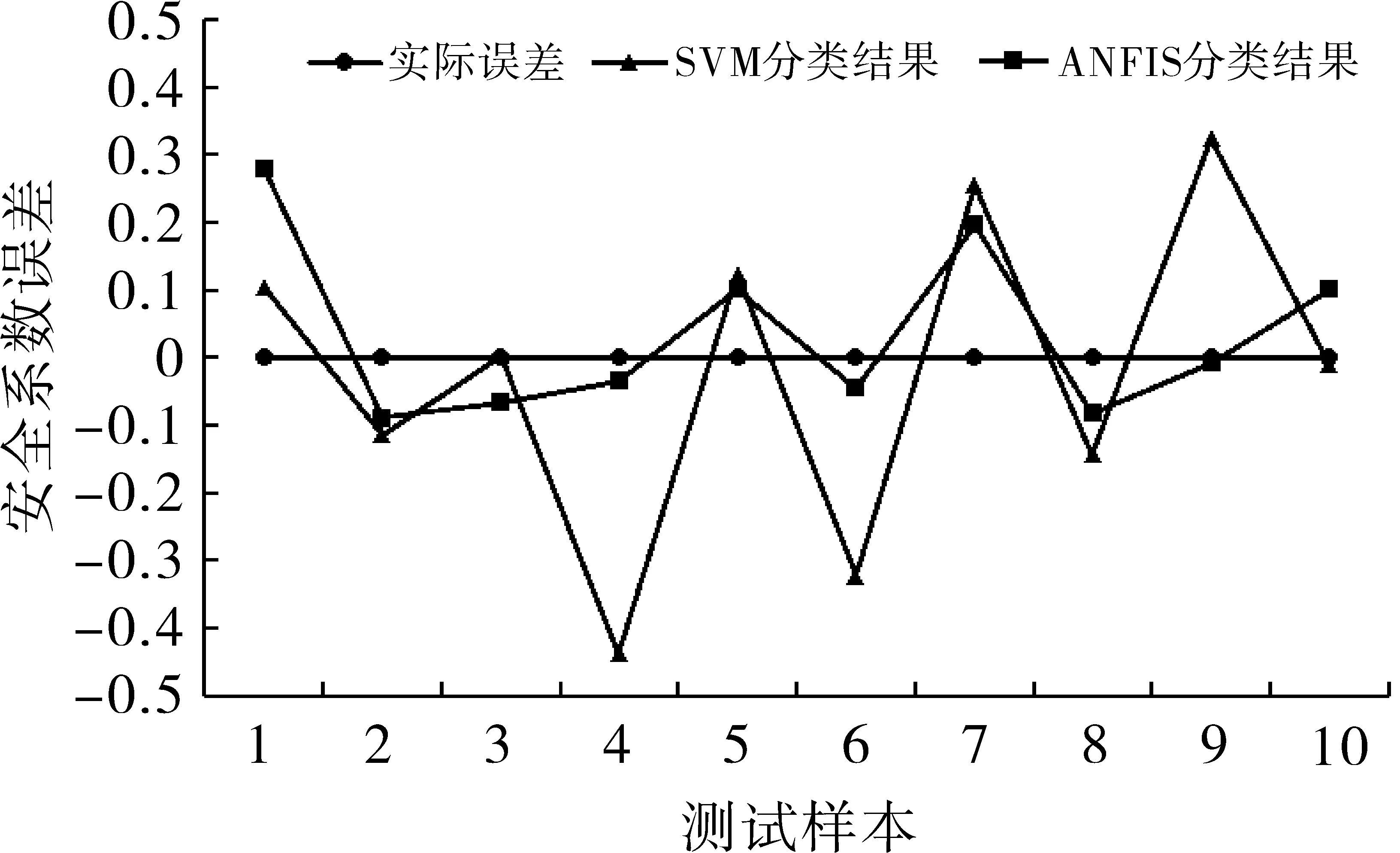
圖4 模型測試誤差比對示意圖

得出SVM分類模型計算預測的安全系數最大誤差值為0.437 8，平均誤差偏差值為0.186 0；ANFIS分類模型計算預測的安全系數最大誤差為0.281 3，平均誤差偏差0.107 8。誤差分析結果表明，ANFIS分類模型的測試結果比SVM分類模型的測試結果更加接近實際誤差，ANFIS分類模型計算預測結果誤差有相對較好的收斂性，可獲得更為相對準確的安全系數預測結果。

4 結語

本文依托泉南高速公路柳州至南寧段邊坡監測項目，針對廣西地質條件和氣候環境，應用常用的SVM分類模型和ANFIS分類模型，在邊坡地質監測數據與邊坡安全系數之間建立一種更有效的、誤差可收斂的數據計算預測模型，采用30個訓練樣本組和10個測試樣本組進行計算預測，并對其結果進行誤差分析比較，得出結論如下：

(1)本文采用非線性分類模型探索邊坡地質監測參數與安全系數的相關性，驗證了非線性分類模型在邊坡監測中應用的有效性。

(2)本文對邊坡形變安全系數計算預測，得出ANFIS分類模型可以獲得相對更為準確的預測結果。

(3)本文僅對廣西的地質和氣候條件進行測試，不同區域的地質類型和氣候條件下，計算預測結果可能存在較大差異性，后續需探究其他分類模型和監測參數的適宜性。