簡(jiǎn)支轉(zhuǎn)連續(xù)小箱梁?jiǎn)瘟红o載試驗(yàn)方法研究

韋宗志，王希瑞，唐洪泉

(廣西交科集團(tuán)有限公司，廣西 南寧 530007)

0 引言

隨著我國(guó)國(guó)民經(jīng)濟(jì)的快速發(fā)展，對(duì)交通運(yùn)輸基礎(chǔ)設(shè)施的需求日益增加。橋梁作為交通網(wǎng)絡(luò)的重要連接樞紐，需要承擔(dān)日益增加的交通量及荷載[1]。簡(jiǎn)支轉(zhuǎn)連續(xù)小箱梁結(jié)構(gòu)由于其具有良好的受力特點(diǎn)、較快的施工速度、成熟的施工技術(shù)等優(yōu)勢(shì)，被廣泛應(yīng)用于橋梁的建設(shè)中。在施工過(guò)程中，由于受到各種因素的影響，可能會(huì)出現(xiàn)與設(shè)計(jì)不一致的缺陷[2]。單梁靜載試驗(yàn)作為評(píng)價(jià)施工質(zhì)量的有效手段，根據(jù)《公路橋梁荷載試驗(yàn)規(guī)程》(JTG/T J21-01-2015)判斷其是否滿足設(shè)計(jì)要求[3]。

目前，對(duì)簡(jiǎn)支梁橋的單梁進(jìn)行了大量的靜載試驗(yàn)研究[4-6]。簡(jiǎn)支轉(zhuǎn)連續(xù)小箱梁在體系轉(zhuǎn)換前后具有不同的受力特點(diǎn)，對(duì)這種類型的橋梁進(jìn)行單梁靜載試驗(yàn)時(shí)，需要將體系轉(zhuǎn)換后的受力狀態(tài)等效成相應(yīng)的荷載施加到單梁上。然而，針對(duì)簡(jiǎn)支轉(zhuǎn)連續(xù)小箱梁?jiǎn)瘟红o載試驗(yàn)的試驗(yàn)方法研究相對(duì)較少。

本文依托柳州經(jīng)合山至南寧高速公路的長(zhǎng)聯(lián)特大橋，提出簡(jiǎn)支轉(zhuǎn)連續(xù)小箱梁?jiǎn)瘟红o載試驗(yàn)的試驗(yàn)方法，基于應(yīng)力等效原則綜合考慮了不同階段的荷載效應(yīng)。

1 工程概況

長(zhǎng)聯(lián)特大橋位于柳州經(jīng)合山至南寧高速公路。該橋梁采用左右分幅結(jié)構(gòu)，上部結(jié)構(gòu)均采用先簡(jiǎn)支后連續(xù)預(yù)應(yīng)力混凝土小箱梁，橋墩采用矩形蓋梁柱式墩或矩形實(shí)體墩，橋臺(tái)采用樁柱式橋臺(tái)，基礎(chǔ)采用鉆孔灌注樁基礎(chǔ)。該橋左線全長(zhǎng)1 125.00 m，橋跨組合為8×(3×40)m+(4×40)m；右線全長(zhǎng)1 205.00 m，橋跨組合為6×(3×40)m+3×(4×40)m。該橋的設(shè)計(jì)荷載等級(jí)為公路-Ⅰ級(jí)，設(shè)計(jì)時(shí)速為100 km/h。左線橋面總寬度為13.00～15.40 m，右線橋面總寬度為13.00 m。本文依托的工程選取第26跨外邊梁為試驗(yàn)梁，如圖1、圖2所示。

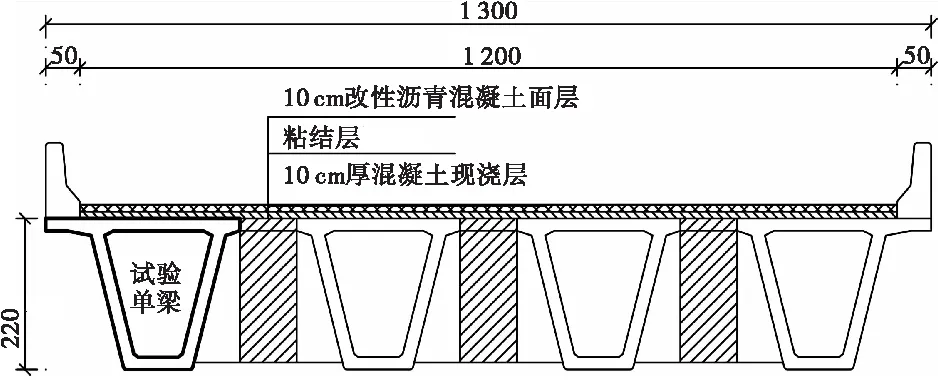
圖1 標(biāo)準(zhǔn)橫斷面圖(cm)

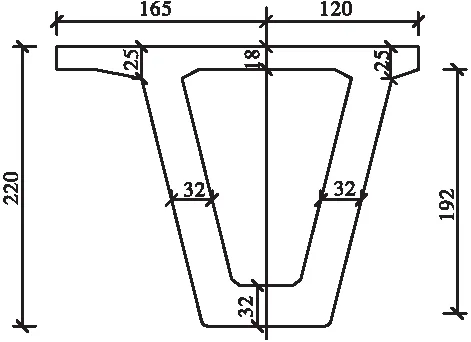
(a)梁端截面構(gòu)造圖

(b)跨中截面構(gòu)造圖

2 基于有限元和等效應(yīng)力原則的試驗(yàn)方法研究

2.1 有限元模型的建立

簡(jiǎn)支轉(zhuǎn)連續(xù)小箱梁在施工過(guò)程中，首先將預(yù)制好的裸梁安裝在臨時(shí)支座上，此時(shí)橋梁處于簡(jiǎn)支的受力狀態(tài)；然后現(xiàn)澆兩片梁之間的現(xiàn)澆帶，拆除臨時(shí)支座，完成體系轉(zhuǎn)換，橋梁的受力特點(diǎn)發(fā)生改變。由于單梁靜載試驗(yàn)往往是在小箱梁預(yù)制后還未安裝就位前進(jìn)行的，試驗(yàn)時(shí)需按照橋梁體系轉(zhuǎn)換后的實(shí)際運(yùn)營(yíng)狀態(tài)進(jìn)行加載。

為了準(zhǔn)確地確定試驗(yàn)控制荷載以及合理的加載方案，根據(jù)簡(jiǎn)支轉(zhuǎn)連續(xù)小箱梁的主要受力階段建立三種類型的Midas Civil有限元模型，分別是小箱梁裸梁模型M-1、包含一半濕接縫和橫隔板現(xiàn)澆帶的小箱梁?jiǎn)瘟耗Ｐ蚆-2以及整聯(lián)的單梁模型M-3，如圖3所示。其中，小箱梁裸梁模型M-1與擬加載的試驗(yàn)梁完全一致。

圖3 單梁有限元模型圖

2.2 基于等效應(yīng)力原則的試驗(yàn)荷載確定

預(yù)制試驗(yàn)梁在架設(shè)就位后，需要承受不同施工階段的荷載。本文分別建立有限元模型M-1、M-2及M-3，用于計(jì)算不同階段的荷載產(chǎn)生的荷載效應(yīng)。并根據(jù)等效應(yīng)力原則，確定在M-1裸梁模型上控制荷載。等效應(yīng)力原則就是通過(guò)在M-1模型上調(diào)整施加的荷載，使箱梁底緣應(yīng)力保持不變，此時(shí)得到的荷載效應(yīng)即作為測(cè)試截面的控制荷載效應(yīng)。

M-1模型為裸梁模型，用于計(jì)算濕接縫現(xiàn)澆部分和橫隔板現(xiàn)澆部分對(duì)跨中截面產(chǎn)生的彎矩效應(yīng)。橫隔板現(xiàn)澆自重G1根據(jù)實(shí)際位置以集中荷載的形式施加到模型上，產(chǎn)生的跨中最大彎矩為M1=76.23kN·m。翼緣板濕接縫現(xiàn)澆部分自重G2以均布荷載作用在主梁，產(chǎn)生的跨中最大彎矩為M2=368.55kN·m。

M-2模型在M-1模型基礎(chǔ)上，建立了濕接縫現(xiàn)澆部分和橫隔板現(xiàn)澆部分，主要用于分析梁端現(xiàn)澆部分G3產(chǎn)生的荷載效應(yīng)。將梁端現(xiàn)澆部分以均布荷載施加在M-2模型上，得到跨中彎矩效應(yīng)M3′=-20.72kN·m，箱梁底緣應(yīng)力σ3=-0.03MPa。由于實(shí)際加載的試驗(yàn)梁是M-1模型，根據(jù)等效應(yīng)力原則，在M-1模型上施加-0.11kN·m的均布荷載，使箱梁底緣應(yīng)力達(dá)到σ3=-0.03MPa，此時(shí)跨中彎矩為M3=-20.6kN·m。

M-3模型是在M-2模型基礎(chǔ)上建立的連續(xù)梁?jiǎn)瘟耗Ｐ停炷连F(xiàn)澆層、瀝青橋面鋪裝和防撞墻以均布荷載G4施加在單梁模型上，得到跨中最大彎矩為M4′=1 290.70kN·m，箱梁底緣應(yīng)力為σ4=1.94MPa。根據(jù)梁底應(yīng)力相等的原則，在M-1模型施加均布荷載，得到跨中彎矩M4=1 266.30kN·m。同時(shí)，在M-3模型上計(jì)算車輛荷載G5產(chǎn)生的彎矩效應(yīng)。依據(jù)橋梁橫斷面布置、主梁截面尺寸以及車道數(shù)量，采用剛接板梁法計(jì)算試驗(yàn)梁的荷載橫向分布系數(shù)，得到車輛荷載產(chǎn)生的跨中彎矩為M5′=2 943.01kN·m，箱梁底緣應(yīng)力為σ5=4.43MPa。同樣，根據(jù)梁底應(yīng)力相等的原則，得到M-1模型中跨中彎矩為M5=2 886.03kN·m。

綜合考慮每個(gè)階段產(chǎn)生的荷載效應(yīng)作為試驗(yàn)荷載的理論依據(jù)，通過(guò)將M-1、M-2及M-3模型分析得到的二期恒載和移動(dòng)荷載產(chǎn)生的跨中彎矩效應(yīng)進(jìn)行組合，得到本文單梁靜載試驗(yàn)跨中截面控制彎矩為4 576.51kN·m。

3 單梁靜載試驗(yàn)

3.1 加載方案

《公路橋梁荷載試驗(yàn)規(guī)程》(JTG/TJ21-01-2015)對(duì)荷載試驗(yàn)的荷載效率ηq規(guī)定如式(1)所示。

(1)

式中：Ss——試驗(yàn)荷載在控制截面產(chǎn)生的最大彎矩效應(yīng)值；

S——控制荷載在控制截面產(chǎn)生的最大彎矩效應(yīng)值；

μ——規(guī)范取用的沖擊系數(shù)。

對(duì)于交竣工荷載試驗(yàn)，規(guī)范規(guī)定荷載效率ηq取值范圍是0.85～1.05。

試驗(yàn)加載采用長(zhǎng)度為12m的鋼筋堆載，布置在跨中12m長(zhǎng)度范圍內(nèi)，加載鋼筋每捆重量為2 850kg。加載布置如圖4所示。

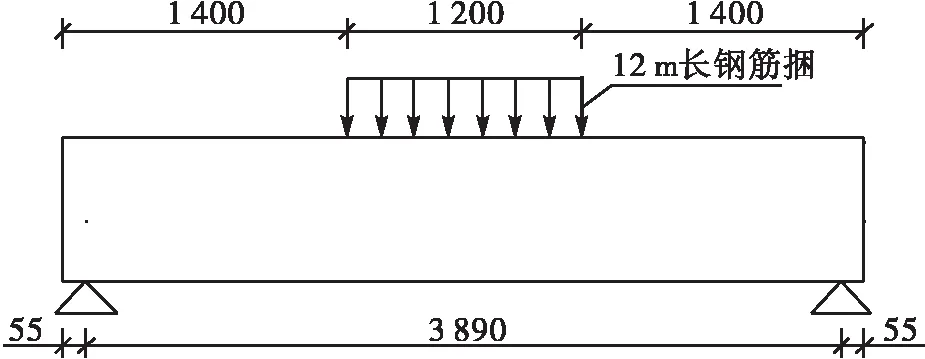
圖4 加載示意圖(cm)

經(jīng)過(guò)計(jì)算，共需要加載20捆鋼筋，試驗(yàn)荷載產(chǎn)生的彎矩為4 599.50kN·m，此時(shí)的加載效率ηq為1.005，滿足規(guī)范的要求。為了保證加載過(guò)程中橋梁結(jié)構(gòu)的安全，采用分級(jí)加載的方式進(jìn)行加載。本次加載共分為7個(gè)工況，具體情況如表1所示。

表1 分級(jí)加載試驗(yàn)統(tǒng)計(jì)表

3.2 測(cè)點(diǎn)布置

本次單梁靜載試驗(yàn)選取跨中截面(L/2)、四分點(diǎn)截面(L/4、3L/4)及支點(diǎn)截面進(jìn)行測(cè)試。跨中截面布置應(yīng)變和位移測(cè)點(diǎn)；四分點(diǎn)截面布置位移測(cè)點(diǎn)；支點(diǎn)截面布置位移測(cè)點(diǎn)進(jìn)行支座壓縮測(cè)試。具體的測(cè)點(diǎn)布置如圖5所示。圖中 “▃”表示應(yīng)變測(cè)點(diǎn)，“▲”表示位移(撓度)測(cè)點(diǎn)。

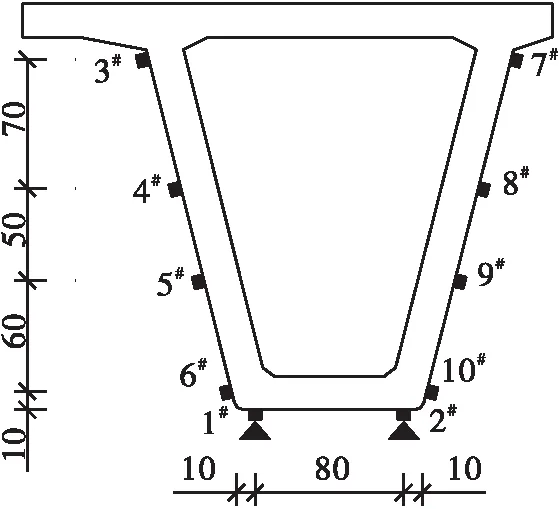
(a)L/2截面應(yīng)變和撓度測(cè)點(diǎn)布置

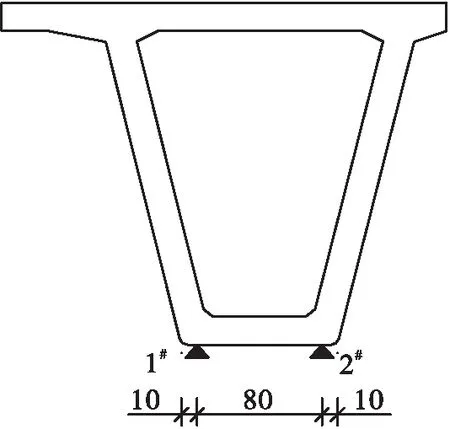
(b)L/4、3L/4、支點(diǎn)截面撓度測(cè)點(diǎn)布置

3.3 應(yīng)變測(cè)試結(jié)果

當(dāng)試驗(yàn)荷載全部施加在單梁上時(shí)，單梁L/2截面應(yīng)變實(shí)測(cè)值和計(jì)算值如表2所示。

表2 滿載條件下跨中截面應(yīng)變?cè)囼?yàn)值與理論值對(duì)比表

從表2中可以看出，單梁跨中截面各測(cè)點(diǎn)的應(yīng)變?cè)囼?yàn)值均小于理論計(jì)算值，校驗(yàn)系數(shù)變化范圍是0.52～0.73，表明試驗(yàn)梁的強(qiáng)度滿足設(shè)計(jì)要求。各測(cè)點(diǎn)的相對(duì)殘余應(yīng)變值在2%～10%之間，不超過(guò)規(guī)范要求的20%，說(shuō)明單梁結(jié)構(gòu)處于彈性工作狀態(tài)。箱梁左右兩側(cè)均布置了應(yīng)變測(cè)點(diǎn)，沿梁高度變化的應(yīng)變分布分別如圖6和圖7所示。

圖6 箱梁左側(cè)沿梁高應(yīng)變分布擬合圖

圖7 箱梁右側(cè)沿梁高應(yīng)變分布擬合圖

由圖6和圖7可以看出，沿箱梁高度范圍內(nèi)，左、右兩側(cè)應(yīng)變均呈線性變化趨勢(shì)，說(shuō)明截面受力特點(diǎn)符合平截面假定。將趨勢(shì)線進(jìn)行線性擬合，左、右兩側(cè)中性軸高度分別為1.356 3m和1.332 6m，而理論計(jì)算值為1.335 8m。實(shí)測(cè)值與理論值基本吻合，也可以說(shuō)明單梁處于彈性工作狀態(tài)。

3.4 撓度測(cè)試結(jié)果

當(dāng)試驗(yàn)荷載全部施加在單梁上時(shí)，單梁各截面的撓度實(shí)測(cè)值和計(jì)算值如表3所示。由表3可以看出，撓度的校驗(yàn)系數(shù)范圍在0.55～0.69之間，滿足規(guī)范中<1的要求，試驗(yàn)梁結(jié)構(gòu)的剛度符合設(shè)計(jì)要求。各測(cè)點(diǎn)的相對(duì)殘余撓度值在3%～10%之間，不超過(guò)規(guī)范要求的20%，也可以說(shuō)明單梁結(jié)構(gòu)處于彈性工作狀態(tài)。從圖8中可以看出，沿梁長(zhǎng)度方向，實(shí)測(cè)撓度變化曲線無(wú)異常值，與理論計(jì)算撓度曲線變化規(guī)律一致。

表3 滿載條件下跨中截面撓度試驗(yàn)值與理論值對(duì)比表

圖8 試驗(yàn)梁撓度實(shí)測(cè)值和計(jì)算值曲線圖

4 結(jié)語(yǔ)

本文依托柳州經(jīng)合山至南寧高速公路的長(zhǎng)聯(lián)特大橋，提出簡(jiǎn)支轉(zhuǎn)連續(xù)小箱梁?jiǎn)瘟红o載試驗(yàn)的試驗(yàn)方法，得到的主要結(jié)論如下：

(1)針對(duì)簡(jiǎn)支轉(zhuǎn)連續(xù)小箱梁?jiǎn)瘟红o載試驗(yàn)控制荷載的確定方法展開(kāi)了理論研究，利用MidasCivil軟件建立模型，考慮了不同受力階段的荷載效應(yīng)，進(jìn)而基于等效應(yīng)力原則確定試驗(yàn)的控制荷載。

(2)跨中應(yīng)變校驗(yàn)系數(shù)變化范圍是0.52～0.73，滿足規(guī)范中<1的要求；相對(duì)殘余應(yīng)變值在2%～10%之間，不超過(guò)規(guī)范規(guī)定的20%，且實(shí)測(cè)中性軸與理論中性軸基本吻合，說(shuō)明試驗(yàn)單梁的強(qiáng)度滿足設(shè)計(jì)要求，加載過(guò)程中處于彈性工作階段。

(3)單梁L/4截面、L/2截面、3L/4截面各測(cè)點(diǎn)的撓度校驗(yàn)系數(shù)范圍是0.55～0.69，測(cè)點(diǎn)的相對(duì)殘余撓度值在3%～10%之間，說(shuō)明試驗(yàn)單梁的剛度符合設(shè)計(jì)要求。