隨機路面激勵下的汽車振動模型分析

蔣欣

（武漢理工大學，湖北 武漢430070）

1 緒論

車輛行駛中，路面不平輸入給予車身不同頻率的激勵，當激勵頻率接近或等于人體器官敏感頻率段時，會引起共振，降低司乘人員的乘坐舒適性。隨著乘用車數量快速增長，道路安全事故呈不斷上升趨勢，尤其操縱穩定性差的車輛易在急轉彎、緊急制動和加速、高速駕駛時發生側翻。懸架系統作為車輛底盤的重要組成部分，其性能對于車輛的乘坐舒適性及操縱穩定性有著至關重要的影響。汽車減震系統的目地是讓汽車在不同平順度的路面上均不產生較大顛簸幅度，使駕駛員和乘客都獲得良好舒適感。減震系統的好壞直接影響乘客及駕駛員對一輛車的滿意度，所以對于一個車企來說進行減震系統的開發與研究是相當必要的。通常路面不平度是汽車振動的基本輸入，解決在隨機不平度的路面激勵下的整車機器零部件振動問題是提高汽車行駛時的平順性、可靠性以及安全性的重要基礎。本文以牛頓第二定理為基礎建立微分方程，從而建立整車的四自由度線性力學平面模型，同時把路面的不平度設置為變量，以模擬汽車在不同路面上行駛。

2 建立數學模型

2.1 假設條件

由于建立的是半車振動模型，為了方便建立微分方程所以作出以下假設：車輪左右兩側的運動狀態相同，汽車車身質量分布均勻，車輪沒有相對于車身的前后位移。以上三條假設為基礎，可將整車運動狀態簡化為圖1中的CAD模型，其物理量含義如表1所示。

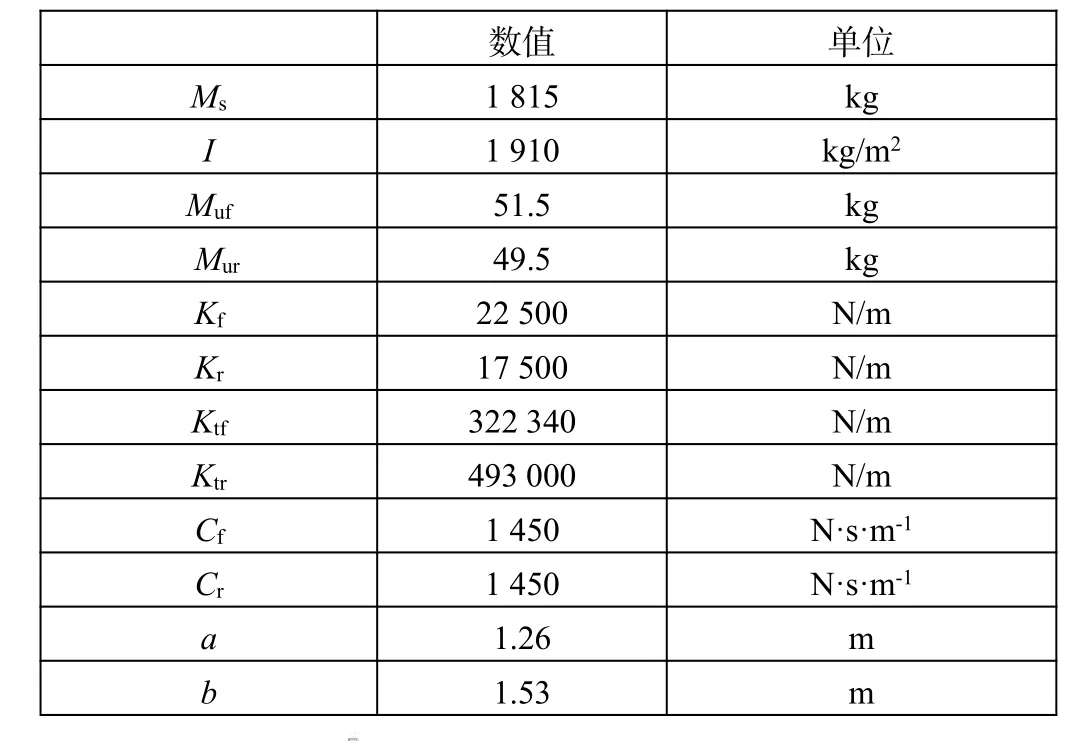
表1 某汽車參數

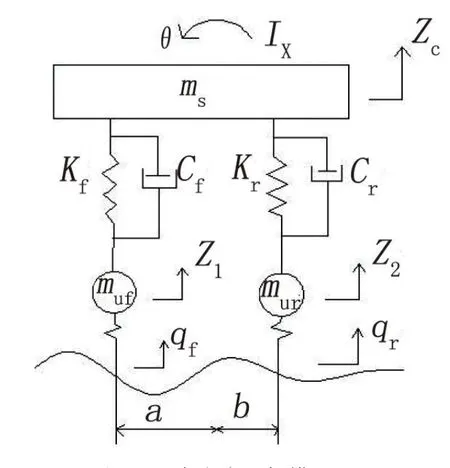
圖1 四自由度懸架模型

2.2 車身模型建立

顯然，如果簡單地根據牛頓第二定律，利用四個微分方程去搭建仿真模型是十分復雜而且難以操作的。下面推導出微分方程的矩陣形式，利用矩陣的形式去搭建仿真模型，使得模型復雜程度大大降低。由四個微分方程可以較為簡單地得到微分方程的矩陣形式：

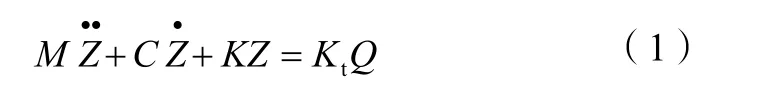
式（1）中：M為質量陣；C為阻尼陣；K為剛度陣；Z為輸出向量；Kt為輪胎剛度陣；Q為激勵向量。

具體矩陣如下所示：

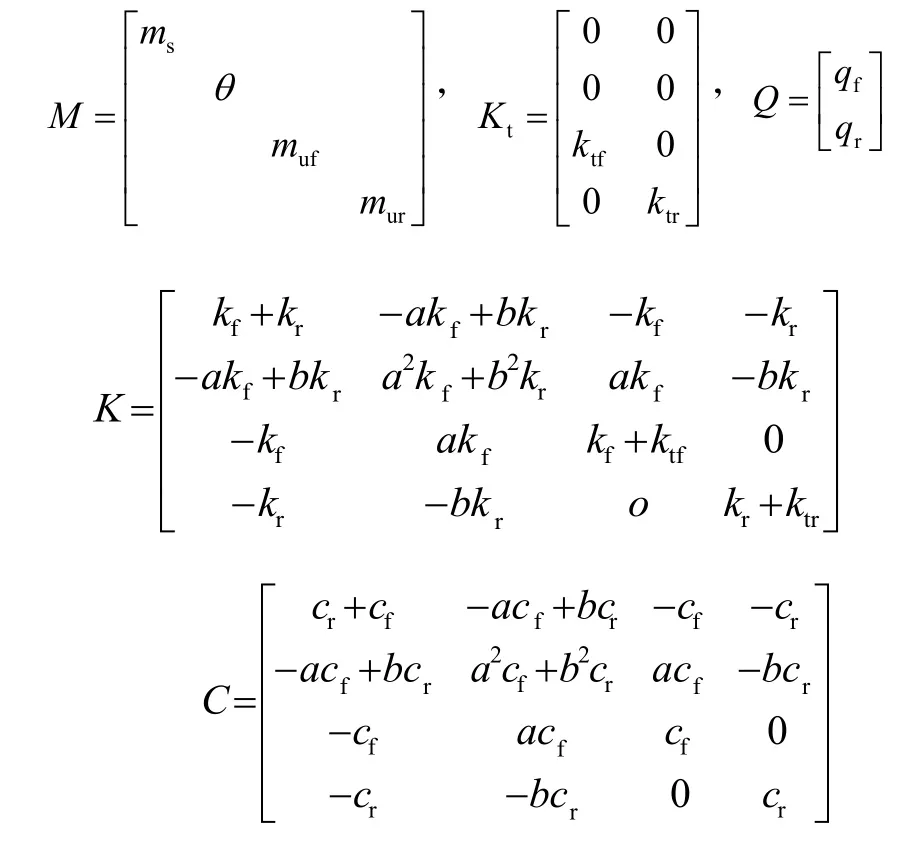
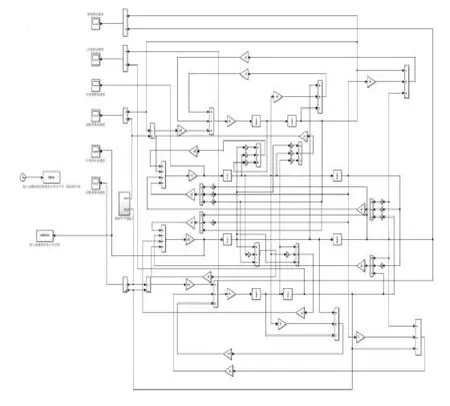
圖2 Simulink四自由度模型

2.3 路面模型

利用Simulink中的白噪聲和延時模塊即可搭建出一個簡單的路面模型，其模型如圖3所示。

3 仿真分析

3.1 車身仿真結果

車身仿真結果如圖4～圖7所示，不難看出，該車的前懸架的震動幅度與頻率要大于后懸架，且相較于后懸架，前懸架振幅的峰值會相比提前0.1 s左右，符合汽車行駛時的真實情況。

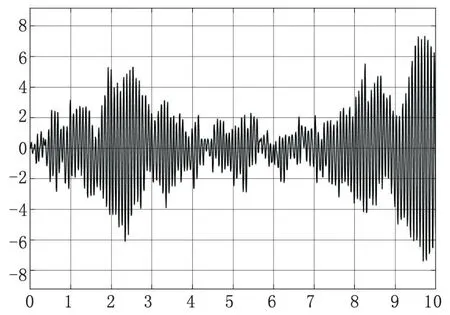
圖4 車身俯仰加速度圖

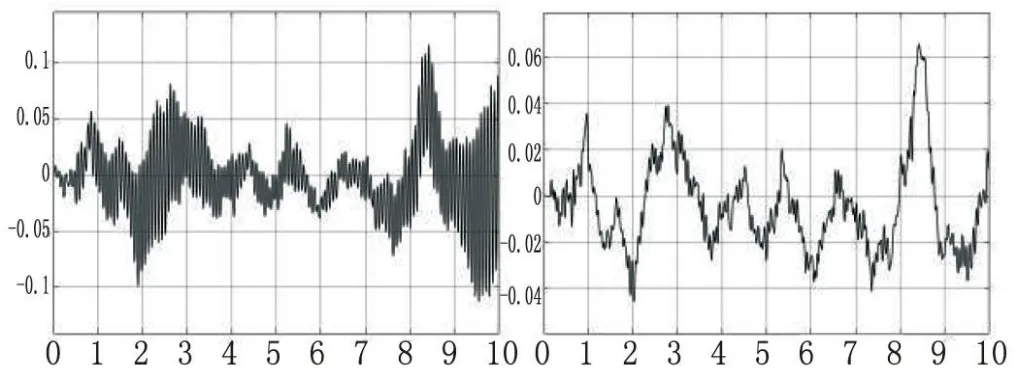
圖5 前后輪胎動撓度圖

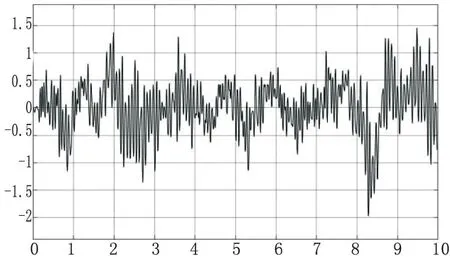
圖6 車身質心豎直方向加速度

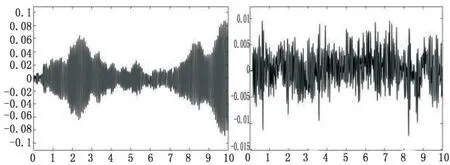
圖7 前后懸架動撓度圖

3.2 幅頻特性

此時微分方程可寫為Mx′′+Cx′+Kx=Kt*q。可以利用MATLAB中的eig函數求特征值特征向量，inv函數取逆。特征值即為固有頻率，特征向量為主振型。接下來通過取拉氏變換求出傳遞函數。

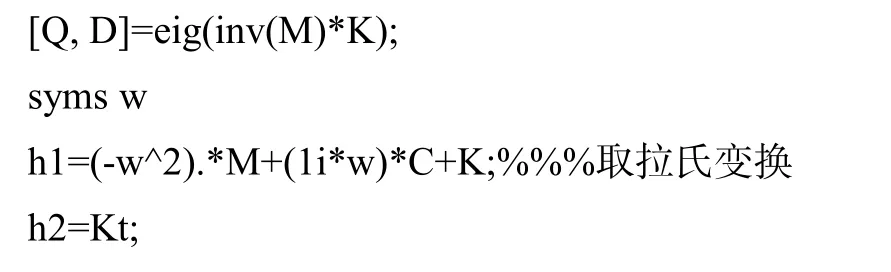
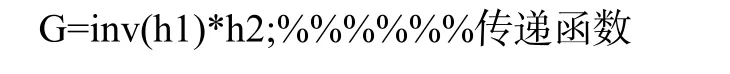
車身垂直振動和車身俯仰運動對前后輪的激勵傳遞函數如圖8所示。

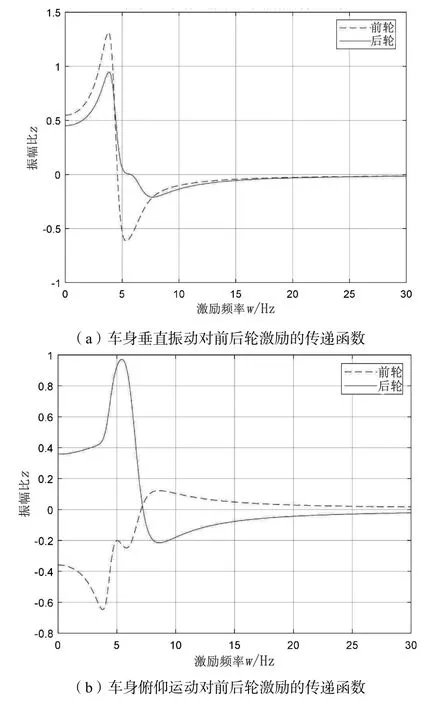
圖8 車身垂直振動和俯仰運動對前后輪激勵的傳遞函數

3.3 改進方案

方案的目標為通過目標函數來降低車身豎直方向上的加速度，最大程度上滿足汽車行駛時的平順性要求。本文主要通過改變前后懸架剛度來改變汽車行駛時的平順性。

約束條件：①前后懸架設計的靜撓度為fc=0～0.30 m，所以前后懸架的剛度極限約束為mfg/0.30≤Kf，mrg/0.30≤Kr，其中mf和mr分別為前后懸架的質量，g為重力加速度。②要滿足汽車平順性要求，乘用轎車為了改善后座的舒適性，常使后懸架的偏頻低于前懸架偏頻，此時有Kf/Kr>mf/mr。所以可以設定改進后的前后懸架剛度分別為Kf=20000，Kr=18000。為了使改進前后的對比更加直觀與清晰，引入了加速度均方根值的汽車性能指標概念。

利用MATLAB程序的運求得改進前和改進后的加速度均方根值分別為accjf=0.4720，accjf2=0.4629。可以看出，在盡量不影響懸架動行程和輪胎上下位移的情況下，改進后車身加速度均方根值減小，車輛行駛時的平順性和乘坐的舒適性得到了改善。

4 結果討論

由圖8可以得知，該車型在前輪的激勵對車身垂直振動的影響較大，后輪的激勵對車身俯仰振動的影響較大。路面激勵為4.8 Hz時，車身垂直振幅和后輪路面振幅比達到最大值；路面激勵為5.1 Hz時，車身俯仰振幅和后輪路面振幅比達到最大值。根據幅頻特性曲線可知，在行車過程中避免路面激勵出現在[3 Hz，10 Hz]的區間內可有效提高舒適性。

5 結語

建立車輛的四自由度模型，模擬道路輸入，運用MATLAB及Simulink進行仿真設計，對車輛懸架系統進行了隨機輸入仿真分析，得到了汽車行駛時懸架的基本參數以及改進前后仿真曲線。以便車輛參數設計人員在設計階段預測車輛的行駛平順性，及時調整參數。文中選擇的四自由度平面模型只考慮了前后輪的輸入，與三維模型相比，不能反映汽車的側傾運動，得到的仿真曲線不能準確反映懸架特性，也不能反映車輛的操縱穩定性能，因此有必要進一步優化分析。本文中利用仿真模型繪制出了前后輪的幅頻特性，得到的結果與事實相符，進一步說明了模型的正確性。本文僅討論了改變汽車懸架剛度來改善汽車行駛時的平順性，但所給出的程序可以仿真任何參數變化之后車輛行駛時懸架數據的變化以及與初始值所做的對比，具有一定的普遍性。因此，為了改善汽車行駛時的平順性，該模型對實際工程中的懸架模擬設計具有一定的參考價值。