基于存貸利差和常彈性方差模型的最優(yōu)投資策略

蔡江佳,李 全

（寧波大學 數(shù)學與統(tǒng)計學院,浙江 寧波 315211）

在實際的金融市場中,由于經(jīng)典的幾何布朗運動模型不能很好地反映市場波動的不對稱性,因此幾十年來許多研究學者提出了各種不同的金融模型來刻畫風險資產的價格動態(tài).Cox 等[1]首次提出了常彈性方差模型,并給出了該模型下的期權價值.在最優(yōu)投資領域,Gao[2]假定風險資產價格滿足常彈性方差模型,并利用Legendre 轉換、對偶定理和變量變換技術得到了退休前和退休后的最優(yōu)投資策略.與Gao[2]研究的問題不同,張初兵等[3]考慮了常彈性方差模型下確定繳費型養(yǎng)老金的最優(yōu)投資問題.夏迪等[4]假設風險資產價格服從常彈性方差模型,但考慮了市場中存在交易成本,得到了風險資產與無風險資產的最優(yōu)投資組合.異質貼現(xiàn)是一種重要的非恒定貼現(xiàn),它描述一個事實,即決策者對從消費和遺產中得到的效用進行貼現(xiàn)是不一樣的,因此Li 等[5]在常彈性方差模型的基礎上進一步考慮了異質貼現(xiàn)這一因素,并得到了最優(yōu)投資策略.同樣假定風險資產價格滿足常彈性方差模型,但Li 等[6]考慮了家庭消費支出為隨機情形時的最優(yōu)資產配置問題.

上述文獻都是在常彈性方差模型下進行研究,且假定存款利率與貸款利率相同.然而,存貸利率可以調節(jié)社會資金的供給與需求,存貸利率的不同很大程度上影響著投資者的收益.常浩等[7]針對不同的借貸利率,根據(jù)投資者的風險偏好,分別采用了三種不同的效用函數(shù),運用動態(tài)規(guī)劃方法得到了最優(yōu)投資策略.常浩等[8]在借貸利率不同的基礎上,將負債過程引入到投資組合問題中,考慮了均值-方差模型下的最優(yōu)投資問題,并給出了有效前沿的解析表達式.王偉等[9]考慮了指數(shù)效用和不同借貸利率情形下確定繳費型養(yǎng)老金的最優(yōu)投資問題.甘少波[10]研究了在不同借貸利率和均值方差準則下確定繳費型養(yǎng)老金的最優(yōu)投資問題.與已有文獻相比,郭文旌等[11]進一步考慮了交易費用,研究了交易費用對最優(yōu)投資策略的影響.高若嘉[12]也考慮了存貸利差情形,但其研究的是家庭最優(yōu)投資消費和人壽保險問題.本文假定借貸利率不同,且風險資產價格服從常彈性方差模型.與甘少波[10]的研究不同,本文研究指數(shù)效用和對數(shù)效用下的最優(yōu)投資問題.

1 金融市場模型

1.1 資產價格動態(tài)過程

式中,r、R分別為無風險利率、貸款利率,且R﹥r.引入符號(x)-=- min(x,0),則上述動態(tài)過程可以寫為

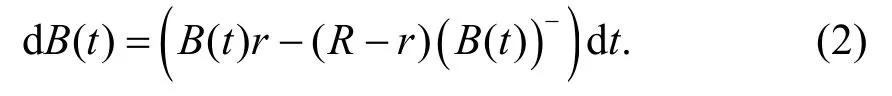
另一種資產是風險資產,將其看成為股票S.S(t)表示該股票在t時刻的價格,假設股票的價格過程滿足常彈性方差模型,該股票的價格動態(tài)過程滿足

式中:μ為股票的預期收益率;b為彈性參數(shù)且b﹤ 0;σS b(t)為股票的波動率,即在t時刻,股票的波動率受到股票價格的影響.

1.2 財富動態(tài)過程

假設投資者在t時刻投資于股票的資金數(shù)量為π(t),用X(t)表示投資人t時刻的財富,則投資在無風險資產上的資金為X(t) -π(t).如果π(t) ﹤ 0,表示賣空股票.如果X(t) -π(t) ≥ 0,表示投資者不需要從銀行借款;如果X(t) -π(t) ﹤ 0,則表示需要從銀行借入資金,借入的資金為因此,財富過程滿足如下微分方程:

其中U(x) 是效用函數(shù).

定義問題(5)的值函數(shù)為

其中邊界條件H(T,x,s) =U(x).

根據(jù)隨機控制理論,得到如下 Hamilton-Jacobi-Bellman (HJB)方程:

式中:H t,H x,Hs為H(t,x,s)關于變量t,x,s的一階導數(shù);H xx,Hss為H(t,x,s)關于變量x,s的二階導數(shù);Hxs為H(t,x,s)關于變量x,s的混合偏導數(shù).

定義集合θ= {(t,x) ? [0,T] ×R|x-π(t) ≥ 0},于是上述HJB 方程可以表示為

對式(8)關于π(t)求導,利用一階最優(yōu)條件可得

解方程(9)得到最優(yōu)投資策略π*(t):

為了計算方便,定義變量δ,當(t,x)?θ時,有δ=r;當(t,x)?θ時,有δ=R.則HJB 方程(8)可以改寫為

結合式(10)和變量δ可得

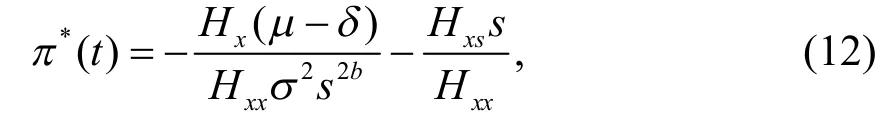
再將式(12)代入HJB 方程(11),可得如下微分方程:

由式(12)可知,為了得到最優(yōu)投資策略π*(t)的顯式表達式,需要解方程(13).

2 模型求解

在經(jīng)濟學中,指數(shù)效用和對數(shù)效用是最常用的兩種效用函數(shù).分別求解指數(shù)效用和對數(shù)效用函數(shù)下的最優(yōu)投資策略.

2.1 指數(shù)效用函數(shù)

假設U(x) 為指數(shù)效用函數(shù),即效用函數(shù)滿足下式:

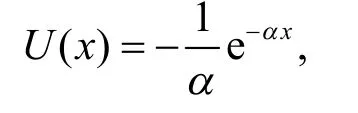
其中α﹥ 0是風險厭惡系數(shù).

投資者的目標是使得終端財富的期望效用達到最大,即

定理1指數(shù)效用函數(shù)下最優(yōu)投資策略為

最優(yōu)值函數(shù)為

其中C(t)和D(t)分別為

證明首先猜測最優(yōu)值函數(shù)H(t,x,s)滿足如下方程:

對式(15)的兩邊關于變量t,x,s分別求一階和二階導數(shù),得

其中Ct是C(t)關于時間t的一階導數(shù),Dt是D(t)關于時間t的一階導數(shù).

將方程(16)代入HJB 方程(13),整理可得

由方程(17)可以看出,只有當變量s-2b的系數(shù)為0 時方程才可以成立,所以得到如下兩個微分方程:

求解方程(18)和(19)可以得到

再將Hx、Hxs、Hxx、C(t)的表達式代入最優(yōu)投資策略式(10),可得

由于借貸的界限為x-π*(t)=0,定義借貸曲線ν(t)的表達式為:

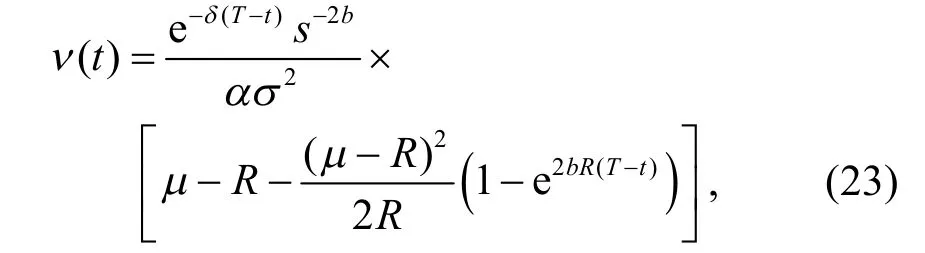
其中θ= {(t,x) ? [ 0,T] ×R|x≥ν(t)},即x≥ν(t)時,投資者不需要貸款;相反,當x﹤ν(t)時,投資者需要貸款,且貸款的金額為

2.2 對數(shù)效用函數(shù)

假定投資者的效用函數(shù)U(x) 是對數(shù)效用函數(shù),即

同樣,投資者的目標是使得終端財富的期望效用達到最大,即

且滿足邊界條件H(T,x,s)= lnx.

定理2對數(shù)效用函數(shù)下的最優(yōu)投資策略為

根據(jù)該變換,可以得到如下關系式:

將式(30)代入式(13)和(12)中,分別得到微分方程和最優(yōu)投資策略π*(t):

現(xiàn)令效用函數(shù)為U(x)= lnx,x﹥ 0,利用Legendre 轉換,可得

引入關于t,s的函數(shù)f(t,s)和關于時間t的函數(shù)q(T-t).再令

將式(36)代入式(33)得到

其中qt(T-t)是q(T-t)關于時間t的一階導數(shù),f t,ftt是f(t,s)關于時間的一階導數(shù)和二階導數(shù).對方程(37)分離變量可得如下兩個微分方程:

再求解微分方程式(38)和(39),得

由于借貸的界限為x-π*(t)=0,定義借貸曲線ν1(t)的表達式為:

得到θ= {(t,x) ? [0,T] ×R|x≥ν1(t)},即x≥ν1(t)時,投資者不需要貸款;相反,x﹤ν1(t)時,投資者需要貸款,且貸款的金額為

3 結論分析與數(shù)值算例

3.1 結論分析

定理1 表明:當投資者的效用函數(shù)滿足指數(shù)效用,且其財富和借貸曲線之間的關系滿足x≥ν(t)時,投資者的最優(yōu)投資策略為式(14)中的第一式;若x﹤ν(t),則為式(14)的第二式.此時投資者需要從銀行借款,借款的金額應為.另外還可以從定理1 發(fā)現(xiàn):(1)借貸曲線與風險厭惡系數(shù)α有負相關關系,即隨著α增大,借貸曲線在減小,這表明風險厭惡系數(shù)α越大,相應的借貸界限會越低,在同樣的財富下,投資者會更愿意向銀行借款;(2)借貸曲線是時間T的減函數(shù),投資期限越長,借貸曲線的值就會越低,從而在其他參數(shù)值一樣的情況下,投資者就會向銀行借款;(3)風險資產的波動率參數(shù)b是借貸曲線的減函數(shù),因為參數(shù)b越大,說明風險資產的波動率就會越大,所以借款曲線在增大.

從定理2 可以得到,當投資者的效用函數(shù)滿足對數(shù)效用函數(shù)時,借貸曲線與各參數(shù)的關系和定理1 中一樣.

3.2 數(shù)值算例

通過數(shù)值計算來分析模型主要參數(shù)對效用函數(shù)為對數(shù)函數(shù)的最優(yōu)投資策略π*(t)的影響,其中取R=0.05,μ=0.06,b=-0 .5,σ= 0.08,x=10,s=2.最優(yōu)投資策略的參數(shù)影響如圖1～3 所示.

圖1 參數(shù)x、μ 對最優(yōu)投資策略的影響

從圖1 可以發(fā)現(xiàn)μ、x與最優(yōu)投資策略之間呈正相關關系.因為μ表示風險資產的預期回報率,當μ逐漸增大時,表示投資在風險資產上的收益會增大,從而投資者愿意加大對風險資產的投資.另外,當投資者的初始財富越多時,投資者自然會增加風險資產的投資數(shù)量,即x越大,最優(yōu)投資策略的值越大.從圖2 中可以得到最優(yōu)投資策略隨著σ、R的增大而減小.σ是風險資產的波動率,波動率越大,說明風險資產的價格波動就會越大,投資者的目標是為了獲得最大的收益,所以隨著σ的增大自然會減少對風險資產的投資.此外,R是貸款的利率,貸款利率越高,投資者越不愿意貸款,因此會減少對風險資產的投資.最后從圖3 可以看到π*(t)和參數(shù)b是負相關的系.從風險資產的價格動態(tài)可知風險資產價格的波動率是關于其價格的一個函數(shù),也就是說價格也會影響波動率.當b小于0 時,參數(shù)b越大則風險資產的波動率就會越小,因此股票價格的市場風險越小,投資者自然選擇加大對風險資產的投資.

圖2 參數(shù)σ、R 對最優(yōu)投資策略的影響

圖3 參數(shù)s、b 對最優(yōu)投資策略的影響

4 結論

本文研究了基于存貸利差和常彈性方差模型的最優(yōu)投資組合問題,通過HJB 方程和最優(yōu)一階條件,得到了指數(shù)效用和對數(shù)效用函數(shù)下最優(yōu)投資策略的解析解.結果表明:(1)投資者是否借貸是由借貸曲線和投資者的財富x共同決定的;(2)在指數(shù)效用函數(shù)下,隨著風險厭惡系數(shù)α和時間t的增大,投資者的借貸曲線在減小;(3)在對數(shù)效用函數(shù)下,借貸曲線與風險厭惡系數(shù)α和時間t均無關,僅與投資者的財富和風險資產的價格有關;(4)在指數(shù)效用函數(shù)和對數(shù)效用函數(shù)下,參數(shù)b均與借貸曲線呈負相關關系.