基于CFSFDP算法的邊緣電力數據異常檢測

張哲敏，李琪林，嚴 平，成貴學

(1.上海電力大學計算機科學與技術學院，上海 200090；2.四川省電力公司計量中心，四川 成都 610045)

0 引 言

如今，隨著智能電網的發展，電力系統中產生的數據量也不斷增多。但安裝在發電、輸電、配電、用電各個環節各種類型的計量裝置和系統，由于外部干擾等原因，會不可避免地出現異常數據，及時有效地檢測出異常數據能夠保障電力系統的穩定性和安全性。各種離群點檢測算法能夠檢測出那些與正常數據行為或特征屬性差別較大的異常數據或行為，有利于降低安全風險，減少經濟損失。

目前，已經有一些文獻研究了電力數據領域的異常值檢測算法。它們可以大致分為基于距離的異常值檢測、基于密度的異常值檢測和基于聚類的異常值檢測等。基于距離的異常值檢測方法由EM Knorr、RT NG[1]等人在20世紀末提出，該方法認為與大多數樣本的距離都大于某個固定閾值的點就是異常值點。但這種方法不能判斷含有密度不同的多個類簇的數據集。基于密度的異常值檢測的原理認為正常樣本點所處的類簇密度要高于異常點樣本所處的類簇密度。最具有代表性的是基于局部異常因子(local outlier faction, LOF)的異常值檢測方法[2]。基于聚類的異常檢測其目標是將數據點按照一定的規則劃分到某一類中，而異常值檢測的目標不屬于任何簇的樣本點k均值聚類算法，據此與正常樣本點進行區別。目前，主要的基于聚類的異常值檢測k均值聚類算法采用k-means和DBSCAN(density-based spatial clustering of applications with noise)算法進行聚類[3-4]。文獻[5]針對傳統電量數據異常檢測方法的不足，提出了一種基于三次指數平滑模型和DBSCAN聚類的電量數據異常檢測方法。文獻[6]采用一種基于孤立森林的異常檢測算法，實現大規模電能量數據的異常檢測。文獻[7]將DBSCAN和LOF算法相結合，即KDBLOF，將k近鄰(k-nearest neighbors，KNN)思想引入到DBSCAN中，解決了原DBSCAN參數確定困難的問題。

電力數據經采集后會將所有數據上傳至集中式數據中心，再使用異常值檢測算法做數據清洗，其中異常數據的傳輸會造成大量的帶寬浪費。在邊緣端進行異常值檢測，可以減少異常數據傳輸，節省帶寬資源。但邊緣端一般不具備較高計算能力的計算處理單元，所以需要復雜度低的算法。

基于密度峰值的快速聚類(clustering by fast search and find of density peaks，CFSFDP)算法是Alex Rodriguez[8]在2014年于《Science》上提出的一種快速尋找聚類中心的聚類算法，具有簡潔、高效、參數少的特點，十分適合在邊緣計算平臺中使用。目前，已有不少研究將該算法應用于電力數據異常檢測。文獻[9]利用 KNN思想重新定義局部密度和距離，將CFSFDP用于電力大數據的異常值檢測，但該方法需要人為設置經驗參數，不具有普適性。文獻[10]采用LOF算法和CFSFDP算法相結合的聚類算法進行電力數據異常值檢測，彌補了CFSFDP算法對于局部密度變化大的數據識別能力弱的缺點；但該方法是通過人工選擇決策圖來實現聚類中心選取，存在主觀因素的影響。

下面將CFSFDP算法應用于電力數據的異常檢測，并提出了一種異常點的選擇策略來實現異常點的自動選擇。所提方法避免了原算法需要通過決策圖人工輸入來實現聚類,再從聚類后的數據中尋找異常點的繁瑣步驟，降低了算法的冗余性并提高了尋找異常值的效率。

1 CFSFDP算法

CFSFDP算法在所提方法中主要基于兩個重要的假設思想：一是假設聚類中心相較于其他的樣本點局部密度較高，且被局部密度較低的點包圍；二是假設各類簇聚類中心之間的距離較遠。為了實現這2種假設，定義了兩種度量方法。

第一個定義是每個點的局部密度，對于每個點i，它的局部密度ρ(i)的表示有2種方法，其中：式(1)為截止距離法；式(2)為核距離方法，適用于數據量較小的數據樣本。

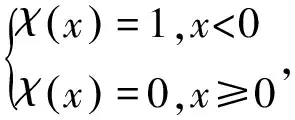
第二個定義是每個點距離高密度點的距離。對于每個點i，它距離高密度點的距離δ(i)的定義公式為

根據定義，只有局部密度較大或者全局最大的點，δ(i)才能夠足夠大。

CFSFDP算法計算局部密度ρ和更高密度距離δ，將數據集映射成二維圖并構造一個決策圖(如圖1所示)。在決策圖中，ρ和δ都很大的點(靠右靠上的點)即為聚類中心。在選擇聚類中心后，再將剩余點分配給距離最近的聚類中心完成聚類。

圖1 CFSFDP算法決策

CFSFDP算法能夠在不確定聚類數目時快速地找到聚類中心，但只適用于特定結構的數據集。對于一些稀疏的數據集，如果經驗參數設置不當，可能會取得較差的效果。此外，由于選取聚類中心時采用人為框圖框選聚類中心的方式，存在主觀因素，不同的選取會得到不同的結果，增加了算法冗余性的同時也不利于實現算法的批量自動化應用。

2 基于CFSFDP算法的異常值檢測

2.1 CFSFDP檢測異常值思路

根據CFSFDP算法提出的假設，從異常值檢測的角度來看，可以認為局部密度較低且距離高密度點較遠的樣本點為異常值點。雖然異常值點距離密度較高的點的距離較正常樣本點遠，但聚類中心之間的距離同樣也很遠。如果此時該聚類中心的局部密度不夠大，很有可能在人工選擇異常值時出現將聚類中心誤劃分為異常值的情況。對此，引入了一個離群值的概念，將樣本點的異常度進行量化，方便進行異常值的選擇。

對于每個點i，它的離群值λi的定義公式為

當點i的局部密度ρi等于0時，此時離群值λi為無窮大，可以直接定義點i為異常值點。其他情況下，λi越高，點i成為異常值點的概率越大。

2.2 異常值點自動選擇策略

通過離群值的定義，為了找出異常值點，可以將離群值大于一定標準的點定義為異常值點。但該標準通常為人工指定，仍然存在主觀因素的影響，所以制定了以下策略來實現異常值點的自動選取。

將所有樣本點按照離群值進行降序排列，取出前m%的點得到離群值排列圖，如圖2所示。可以看出，雖然離群值整體呈現下降趨勢，但下降的程度有所不同，前面下降得快，后面下降得慢。即前半部分離群值相差大、不穩定，可以認為是異常值點；后半部分因為趨向穩定，離群值下降緩慢，可以認為是正常點。在下降程度發生最大變化的點是離群值總體下降由急變緩的拐點。拐點前的是異常值點，拐點后的是正常樣本點。

圖2 離群值降序排列

當表示下降趨勢時，可以采用斜率進行表示，即

式中，ki，m表示區間[i,i+m]內的離群值λ變化率，該參數描述了這一區間λ的總體變化趨勢。

對于某點前后下降趨勢，可以用與前一點線段的斜率和后一點線段的斜率的比值來表示。

第一個點的下降趨勢默認為0，且當該點的離群值與后一點相同時，該點的變化趨勢與前一點相同。計算所有點的變化趨勢比值，繪制出圖3所示的變化率趨勢圖。拐點為使變化率k取得最大值時的點。

圖3 變化率趨勢

得到拐點后，可將拐點前的所有點，視為異常值點，使用CFSFDP算法尋找異常值點的具體步驟如下：

1)根據dc確定每一個點的局部密度ρi和距離δi。 2)計算每個點的離群值λi并從高到低排序。

3)取樣本點前m%的點計算變化趨勢ki。m為經驗參數，一般選擇5%～10%。

4)取使k取得最大值的拐點x。

5)挑選出拐點之前的點{1,2…,x}作為異常值點。

3 仿真驗證

采用2017年1月至10月某公司的日用電數據作為研究對現象，采樣間隔為15 min。用戶日用電數據作為電力數據的一種，經常因為電能表故障和傳輸異常等原因，造成上傳數據存在異常。但在電力數據的異常值檢測場景中，異常值所占比例遠低于正常對象。因此，只提取了數據集中的部分數據，使得最終實驗數據中異常值與正常值的比值滿足異常值檢測的一般要求。并且，為了衡量用電數據異常檢測算法的有效性，采用的數據提前進行了人工標注，即異常數據已經被標識，方便檢驗異常檢測算法的效果。

在預處理階段對數據進行了降維和歸一化處理，是為了消除因為量綱不同和數量級差距所帶來的影響，且可以加快算法的識別速度。按照式(7)對數據進行歸一化處理。

(7)

為了評估基于CFSFDP尋找異常值算法的性能，與DBSCAN直接檢測異常值、局部異常因子LOF算法進行了對比試驗。DBSCAN直接檢測異常值是先對數據進行聚類，獲得不同的類簇；然后求取各個類簇聚類中心間的距離，如果距離過大則認為是異常用電數據。這里設置DBSCAN的參數ρ為0.2。

將算法檢測出的異常值與數據樣本的真實標簽作對比，計算并選取檢測率(detection rate)和誤檢率(false positive rate)作為算法評價標準，檢測率和誤檢率的計算公式如下：

(8)

(9)

檢測率和誤檢率的實驗結果如圖4、圖5所示。由圖可以看出：1)基于CFSFDP算法的異常檢測在檢測異常值時總體檢測率較高，誤檢率較低，明顯優于直接利用DBSCAN算法檢測異常值和利用局部異常因子算法LOF檢測異常值；2)對于不同月份的檢測樣本，直接利用DBSCAN算法的異常檢測算法的檢測率和誤檢率不同且波動較大，這是因為算法對不同數據樣本具有獨特性，DBSCAN只適用于部分樣本。相對地，基于CFSFDP算法的異常檢測就具有較好的適應性，對于不同月份的數據都能維持一個很高的檢測率和很低的誤檢率，變化不大。其中部分月份檢測率較其他月份有所降低，原因為該月平均用電量較其他月份有差別，需要提取更多該月樣本進行單獨檢測。

圖4 檢測率實驗結果

圖5 誤檢率實驗結果

同時，基于CFSFDP算法的異常檢測還具有快速查找異常值的特點。在實驗內存為8 GB、CPU為1.6 Hz的運行條件下，3種算法的計算耗時如表1所示。

表1 3種算法的計算時間

從表1可以看出，基于CFSFDP算法的異常檢測運行時間是比其他兩種算法都要短。這不僅證明了基于CFSFDP算法的異常檢測可以減少計算量，具有快速找到異常值的特點，而且證明了其對大規模數據集具有更好的適應性。

綜上，所提出的基于CFSFDP算法的異常檢測同時具有檢測率高、誤檢率低和運行時間少的特點。在電力生產、調度和決策過程中，可以起到良好的監督防范作用。在用戶防竊電方面也能為電力企業提供有力的依據，能夠更好地為電力生產和電力繳費服務。

4 結 語

上面對于電力數據的異常檢測問題進行了研究，提出了一種基于CFSFDP聚類算法的電力數據異常值檢測方法。該方法基于原本的密度峰值快速搜索算法提出的兩點有關于聚類中心的假設，設立了離群值指標，在該指標的判斷下尋找異常值點，實現了異常值點的快速尋找。同時根據離群值下降趨勢，提出一種不需要進行人工選擇的自動選擇異常值點的策略，避免了進行人工選擇時主觀因素的影響。通過對比該方法與利用DBSCAN直接尋找異常值和利用局部異常因子LOF尋找異常值的方法，發現該方法能夠有效、快速地尋找出異常值點，且該算法復雜度低，耗時短，適合作為邊緣設備檢測電力數據的算法。