小樣本條件下裝備作戰效能評估問題研究*

張家賓

（91404部隊 秦皇島 066000）

1 引言

在武器裝備發展建設過程中，裝備性能試驗的測試及評估分析對于裝備的改進、提升及指導部隊的作戰使用都具有重大意義。作戰效能評估一般指武器裝備在相應的作戰背景下，針對具體的作戰對手構建近似于實戰的、逼真的試驗環境，綜合進行作戰能力的評估。評估結果可以識別并評估裝備的設計和使用缺陷，為新裝備作戰使用提出建議，為裝備的列裝定型提供決策，同時在裝備的作戰適用性、體系貢獻率和作戰效能方面給出結論。作戰效能的評估方法眾多，包括層次分析法、ADC法、指數法等，每種方法均需要構建作戰能力指標體系并將指標定量化。對能力指標的定量化需要基礎數據做支撐，但長期以來由于兵力短缺、靶標保障困難、復雜環境難以構設等因素限制，作戰效能評估一直面臨著樣本量不足的問題。通過一次或少量幾次試驗也很難獲得一些復雜環境、邊界條件下的試驗數據，無法用概率統計的方法進行試驗結果的評估。針對上述問題，一般根據原始數據或小樣本的數據特征擴充樣本量，在大的數據基礎上再進行后續能力特征分析。

對于處理小樣本數據條件下的能力特征問題，工程上已經有很長的應用經驗。傳統的數據樣本量擴充方法按是否存在先驗信息即了解數據的統計規律信息大致分為兩類。對于有先驗信息的數據樣本可以采用Bayes方法擴充樣本量。對于不了解數據特征規律的樣本量，一般選用Bootstrap方法來擴充樣本量［1］。由于作戰試驗獲取的數據多為無統計規律的數據，文章采用的是Bootstrap方法進行樣本量擴充，下面介紹其基本數學原理，并針對存在的適用性問題引入改進的Bootstrap方法。

2 兩種樣本量擴充方法的數學原理

2.1 Bootstrap方法

Bootstrap方法是一個傳統小樣本量擴充方法，該方法為一個再抽樣過程，通常也稱為計算機增強型統計推斷過程。該方法是在小樣本分析中經常使用該方法，其基本原理通過數理統計方法構建基于現有小樣本數據的統計分布，對樣本的統計分布規律參數進行評估，將小樣本問題轉化為大樣本問題，其一般步驟如下［2～3］。

取試驗中所得原始試驗數據樣本序列為X=(x1，x2，…，xn)，該樣本數據量有限，我們稱該樣本為原始樣本。

令xi～F(x)，i=1，2，…，n，

F(x)為經驗分布函數。

由這些原始樣本構造的經驗分布函數一般形式如下：

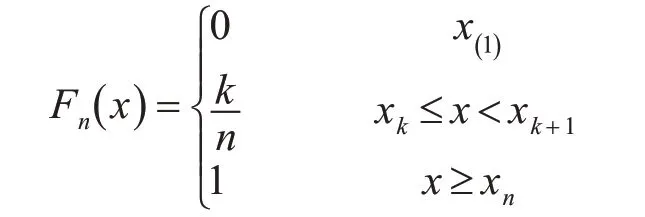
其中，x(1)≤x(2)≤…≤xn是一組順序統計量，是x1，x2…，xn按從小到大排列后得到的數據序列。

利用上述經驗分布函數Fn來構造N組新的樣本數據，即抽取新的試驗樣本，方法如下：

取區間為0～M（M?n），η為計算機產生的隨機數（η取整數且具有獨立性、均勻性）。

令i=η%n，

在觀測值中找到對應下標為i的樣本xi作為新生成樣本x*，則x*為所需的新的隨機樣本序列值。

這N組新樣本為

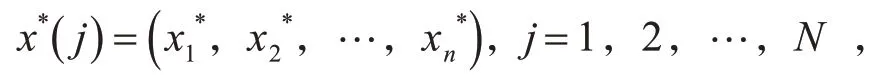
我們稱這些樣本為自助樣本。

引入Rn如下：

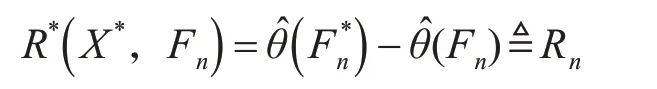
Θ為樣本分布的特征值，θ^為特征值估計。由于根據小樣本試驗很難求出θ(F)，上式中用θ^(F)近似代替θ(F)。

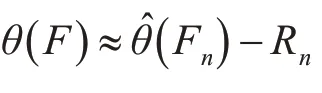
Bootstrap方法是通過構造經驗分布函數，再利用隨機數挑選構建新的樣本序列。對新構建的統計序列進行參數估計，積累參數估計的值，統計參數的分布規律進而得到樣本的參數估計值。該方法原理清晰，計算步驟簡單，是實際的樣本數據擴充中經常用到的方法，但由于該方法為樣本的重復再抽樣，所以導致所生成的自助樣本中原樣本點的重復率偏高，最終的參數估計不準確。針對該問題引入下面的Bayes Bootstrap方法。

2.2 Bayes Bootstrap方法

引入Bayes Bootstrap的數據生成方法，對上述Bootstrap的樣本擴充方法進行部分改進，使得擴充后數據對原始樣本點的重復率降低［5～9］。其數學原理如下。

設原始樣本為X=( )x1，x2…，xn，該樣本量是有限的，則利用Bayes Bootstrap方法生成自助樣本的方法步驟如下。

取服從于Dirichlet分布的隨機變量：

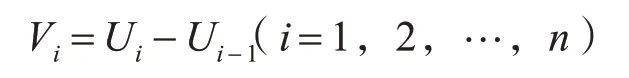
其中U0，U1，U2，…，Un-1為服從于（0，1）均勻分布的隨機數，取U0=0，Un=1。

那么有

V1+V2+…+Vn=1

則該樣本的平均值估計為

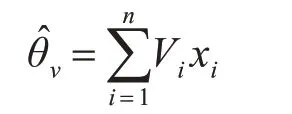
重復上述步驟，逐步得到均值和方差的平均值。

Bayes Bootstrap方法通過構造服從于Dirichlet分布的隨機變量，使新生成樣本為原始樣本按隨機概率生成，然后通過多次迭代來生成自助樣本，使得新樣本中原樣本點出現率大大降低，一定程度上消除了新樣本的偏向性特征，在樣本數據擴充方面比改進前更有優勢。

3 模型驗證及效果對比分析

給出已知分布規律的小樣本數據，利用上述兩種方法模型分別進行數據樣本擴充并計算分布特征的估計值，然后進行對比，分析兩種方法的實際應用效果。

取服從于正態分布N（2，1）的樣本數據列為（1.7586，2.3192，2.3129，1.1351，1.9699，1.8351，2.6277，3.0933，3.1093，1.1363）

利用Bootstrap方法擴充原始樣本的數據量，若將數據擴充為100組，利用Matlab畫出統計的直方圖如圖1所示。

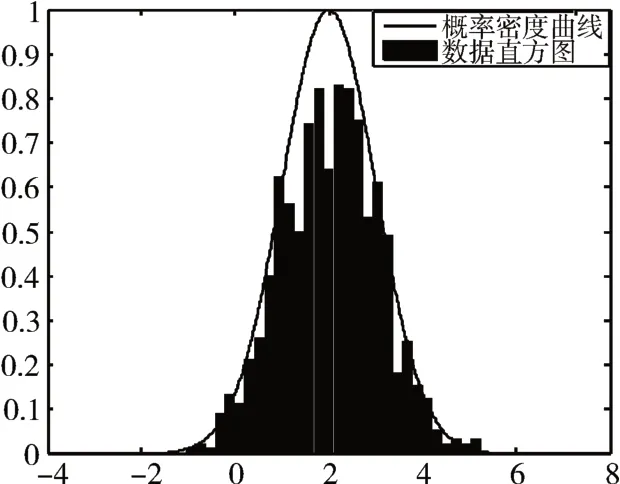
圖1 自助樣本統計特性驗證圖

從圖上可以看出新生成的樣本分布近似接近于原分布的特征。為進一步對比兩者的參數估計效果。分別用Bootstrap、Bayes Bootstrap方法擴充原始樣本生成自助樣本，并對新樣本做均值參數估計和區間估計，取0.95的置信度，計算結果如表1所示。

表1 兩種方法所做參數估計和區間估計對比表

對比兩種方法在對小樣本數據的特征值估計方面的效果，兩種方法產生的估計特征值和原始分布相比均值誤差分別為0.0052、0.0032，區間估計長度分別為0.0082、0.0070。兩種方法得到的誤差值都在誤差范圍內，樣本都服從相應參數下的正態分布，表明兩種方法在對小樣本條件下的參數估計都符合原分布特點。同等條件下，改進的Bayes Bootstrap方法比Bootstrap方法，均值參數估計誤差更小，區間估計長度更短，表明改進的Bayes Bootstrap方法在小樣本參數估計方面能更精確。這也驗證了改進方法通過多次迭代生成的自助樣本，使得新樣本中原樣本點出現率大大降低，從而使參數估計效果更有優勢。

4 對空攔截能力作戰效能評估研究

將Bayes Bootstrap方法應用于某艦艇參加作戰試驗鑒定時對空攔截能力的作戰效能評估。由于試驗成本、兵力短缺、環境構設復雜等因素限制，對空攔截試驗數據采集不充分，為提高試驗結果置信度、增加對空攔截能力考察的全面性并綜合考評裝備系統的效能，考慮通過Bayes Bootstrap方法擴充樣本量，在大樣本量下進行數據分析及參數估計，迭代若干次參數估計的數值后取平均值來確定最終的參數值。

對空攔截的作戰效能評估應首先構建對空攔截作戰能力指標體系。體系的建立應以艦艇的使命任務為牽引，從裝備的性能指標出發，綜合考慮作戰樣式、作戰對手及作戰環境等因素。結合本艦性能特征分析上述因素后，從艦艇對空信息感知、指揮控制、打擊概率、毀傷效果等方面進行考慮［10～12］，構建該型水面艦艇能力指標如圖2所示。

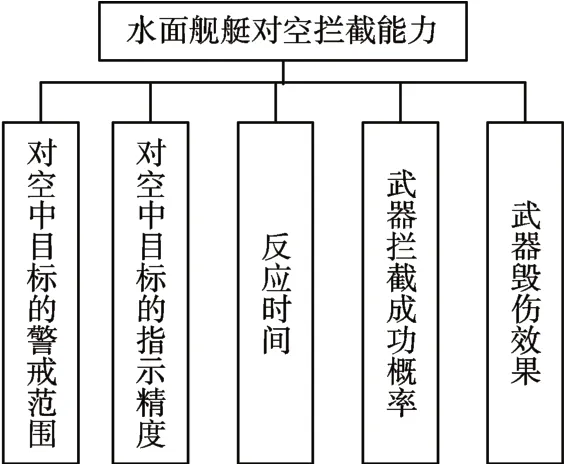
圖2 對空能力指標圖

作戰效能評估可以采用指數評估法、層次分析法、ADC法等，此次評估采用最常用的指數法。該方法首先需對評估體系中的各項指標進行量化，然后進行各指標間的權重分配計算，最后進行指標權重的加權和確定最終的評估值。

以上述指標中的精度指標為例，將對空探測距離精度值（RMS）按距離分段，在不同航次的同一距離段，對測量值和真值進行數據處理獲得在各個航次下，探測距離精度值如下：

（0.05，0.06，0.08，0.03，0.10，0.07，0.05）

考慮到能力指標的正比例關系，對精度值進行正比例處理得到：

（0.95，0.94，0.92，0.97，0.90，0.93，0.95）

利用上述的Bayes Bootstrap方法對精度樣本進行擴充并分析精度樣本的特征值。

原始樣本數據為

X=(x1，x2…，xn)=(0.95，0.94，0.92，0.97，0.90，0.93，0.95)

取服從于（0，1）均勻分布的隨機數序列U0，U1，U2，…，Un-1為

（0，0.13，0.22，0.38，0.55，0.62，0.70，0.91，1）

那么有服從于Dirichlet分布的隨機變量

V1，V2，…，Vn=Ui-Ui-1=(0.13，0.09，0.16，0.17，0.07，0.08，0.21，0.09)

滿足：

V1+V2+…+Vn=1

計算該樣本的平均值參數估計為

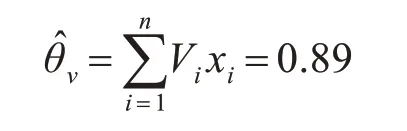
樣本方差估計為

重復上述步驟五次，進行迭代，最終得到平均值和方差值的估計值見表2。

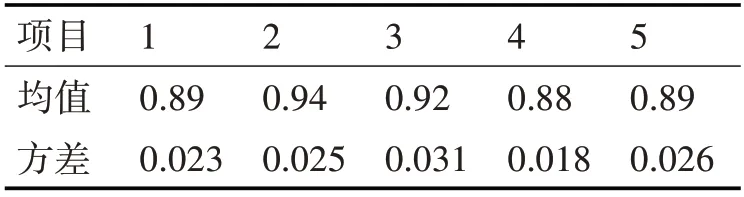
表2 五次平均值和方差迭代表

對五組數據取平均值后最終的均值和方差的為

同理，根據上述方法可以得到對空攔截能力指標體系內其他指標經Bayes Bootstrap方法處理后得到的估計值，令計算得到的各指標能力值為Ki（其中i為指標個數）。指數法進行作戰效能評估還需要進行各指標權重的計算，一般利用專家打分法確定體系內各指標的權重ωi并經過判斷矩陣檢驗其一致性，則該型水面艦艇最終的作戰效能評估結果為

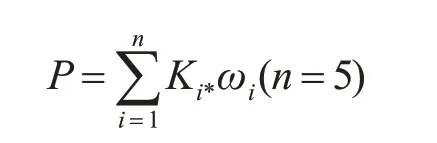
評估結果是在相應作戰背景下，對作戰對手的能力評價，對部隊有針對性的改進戰法、提高訓練效果具有重要的指導意義。

5 結語

針對作戰效能評估處理中一直存在的樣本量不足的問題，文章對比了傳統的Bootstrap和改進的Bayes Bootstrap樣本擴充方法，驗證了Bayes Bootstrap方法在參數估計和區間估計方面的精確性，并將該方法成功應用于某型艦艇的對空攔截能力的作戰效能評估中，提高了結果的置信度。但該模型并不能應用于成敗型試驗（即10問題）的效能評估，而該類試驗往往為導彈射擊等高消耗試驗，對其作戰效能評估具有重大的參考意義，這也是下一步要研究的方向。