基于EEMD-多尺度排列熵-SVM的小電流系統故障選線仿真*

林海濤 曹春誠

（國網呼倫貝爾供電公司 呼倫貝爾 021100）

1 引言

我國的配電網主要應用小電流系統，又稱為中性點不直接接地系統。在小電流接地系統中，單相接地故障發生的概率較高，2h～3h不能排除故障的話，將會帶來更加嚴重的后果，影響電網正常運行。小電流系統發生故障時，故障信號微弱，線路上的電流變化不明顯，零序電流也呈現出復雜的非線性f和非平穩性，給故障選線帶來困難［1～4］。

目前國內外故障選線主要分為兩大類，一是利用穩態信號的大小和相位方向進行故障選線；二是利用暫態信號的突變量、大小、相位、能量進行選線。相對于穩態故障選線法，暫態信號的信息量更加豐富，故障特征也更加明顯，因此暫態選線法得到更多的認可，目前的選線方法有信號注入法，通過電壓互感器向線路注入特定頻率的信號完成選線，但是注入法受到高阻接地限制；零序電流幅值法，利用故障時零序電流幅值最大完成選線，但是在諧振接地系統中，該方法失效；小波變換法，根據小波變換的分頻特性，將信號投影到小波頻帶上，根據頻帶上信號的大小和極限的比較，判斷故障線路［5～7］，在中性點不接地和消弧線圈接地系統中得到應用，但是短路時暫態信號有隨機性，如果暫態信號太小，小波分析法會有很大的誤差。受過渡電阻干擾，信號對突變信號干擾影響也比較大；Prony算法此算法分析小電流系統的故障電流有很好的普適性，當小電流系統發生單相接地故障時，故障電流的幅值、頻率、阻尼系數等參數和故障的特征有很好的相關性，該算法可以分析直流分量的阻尼和高頻率分量的頻率，通過這樣的特征就可以實現故障選線了，但是Prony算法需要很大的計算量，而且對微機的性能具有較高的要求；行波法故障測距用的是故障的時候所產生的行波信號，當線路發生故障時，會在線路兩端傳遞暫態行波信號，其中包括單端法和雙端法，行波法在分支少和較長線路的輸電線路具有很好的適應性，但是如果配電線路結構復雜，分支多的短線路，則識別會困難，而且需要很多行波檢測設備，經濟成本也會很高，因此在配電網中行波法很難適用［8～11］。

提出EEMD-多尺度排列熵-SVM選線方法。EEMD算法是通過對原始多次加入白噪聲之后在進行EMD分解，將所得結果平均得到各個固有模態函數，EEMD算法抑制了EMD算法的模態混淆問題，通過EEMD算法對信號分解，可以得到從高頻到低頻的固有模態函數，并且所得結果相比于EMD算法更具有固有模態函數性質。多尺度排列熵是一種動力學突變檢測方法，可以對信號復雜程度分析較為理想，可以充分分析信號的特征。SVM對解決非線性、高維度樣本分類，分類效果良好。

用EEMD對各線路的零序電流進行精細的分解，得到各固有模態函數，用多尺度排列熵計算各線路的固有模態函數各個尺度下的排列熵，將計算出來的多尺度排列熵作為SVM的輸入，通過SVM輸出的分類標簽判斷故障線路。

2 EEMD分解方法

由于EMD算法處理暫態信號時會受到突變干擾，出現模態混淆問題，使所得的固有模態函數分量失去信號本身的物理意義。而EEMD算法通過添加不同的高斯白噪聲和多次集合平均克服了EMD的模態混淆問題。具體步驟如下。

1）在信號x（t）疊加高斯白噪聲ni（t），其中高斯白噪聲的均值為零，標準差為信號x（t）的0.2倍，即：

2）用EMD算法分解X（t），得到各固有模態函數分量，即：

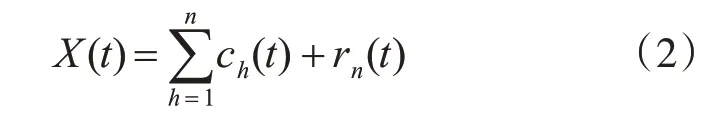
其中，ch（t）為EMD第一次分解得到的h個固有模態函數分量，rn為余項。

3）在x（t）中再次加入高斯白噪聲，重復上述步驟1）、步驟2）。

4）重復步驟k次，會得到k組IMF分量，將所得結果平均。得到的固有模態是按照高頻到低頻順序排列的。

3 多尺度排列熵

多尺度排列熵是對排列熵的一種改進，首先需要對時間序x（i）列粗粒化，即：

式中，s代表尺度因子，ys（j）代表多尺度下的時間序列，對時間序列進行重構得到：

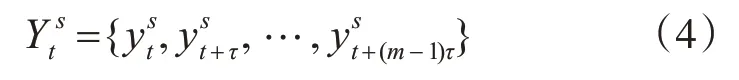
其中，m代表嵌入維數，τ代表延遲時間。將（4）按照升序排列，則多尺度時間序列有m！種排列方式，計算各個尺度下時間序列的概率：

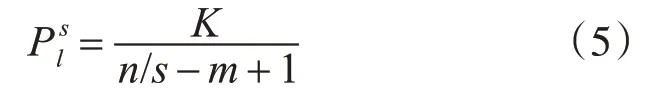
其中，K代表每種類型出現的次數，則各尺度下的排列熵為

將式（6）歸一化，即：

多尺度排列熵可以衡量時間序列的復雜程度，不同故障情況下，各個零序電流的時間序列測度設不同的。小電流系統故障時，會產生各線路不對稱運行，會產生零序電流，用EEMD算法對零序電流分解，得到各個固有模態分量，取各個線路分解后的固有模態函數，計算多尺度排列熵。其中粗粒化過程十分關鍵，即尺度因子的選擇尤為重要，通過多次實驗發現，尺度因子取5時，實驗效果最佳。計算出來的多尺度排列熵作為SVM的輸入。文中采用遺傳算法改進的SVM。

4 GA-SVM算法

SVM可以解決非線性、高維度樣本的分類，對于小電流系統故障各線路的信號多尺度排列熵有良好的分類效果。SVM需要構造一個分類超平面：

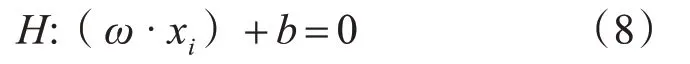
通過相應的約束條件得到分類間隔：

在對樣本完成分類時，需要加入從松弛變量和懲罰因子，得到最優的超平面：

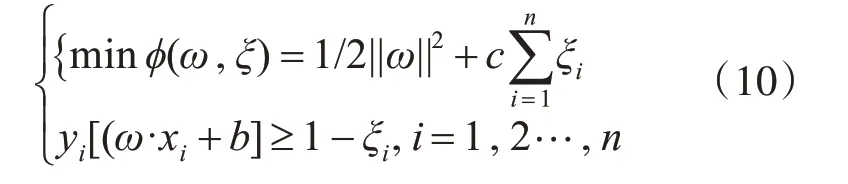
其中，ξ為松弛變量，c為懲罰因子，x，y為輸入樣本。

RBF為SVM的核函數，其中的盛飯系數和核參數都需要進行優化，本文采用遺傳算法對其進行優化。遺傳算法具有自適應全局搜索能力，是模擬生物界遺傳和進化而得到的算法，通過遺傳算法對SVM進行優化可以使得SVM分類更加準確，提高故障選線能力。具體步驟如下：

1）通過對懲罰系數和核參數編碼，生成初始種群。

2）用多尺度排列熵作為樣本對SVM進行訓練，得到分類結果，計算分類的準確程度，建立適應度函數。

3）滿足停止條件時，得到優化后的懲罰系數和核參數，如果所得結果不滿足，進行下一次遺傳迭代。

5 仿真驗證

配電系統選擇四條線路，線路長度分別為10km、25km、35km、40km，系統采用經消弧線圈接地方式，其中采用10%的過補償，因此取消弧線圈的電感L=0.9459H，線路的正序和零序參數如下所示。

R1=0.01273Ω/km，R0=0.3863Ω/km

L1=0.9337mH/km，L0=4.1264mH/km

C1=12.74nF/km，C0=7.751nF/km

假設線路1的A相在出線的20km處發生接地故障，且接地電阻為50Ω，各線路零序電流如圖2所示。

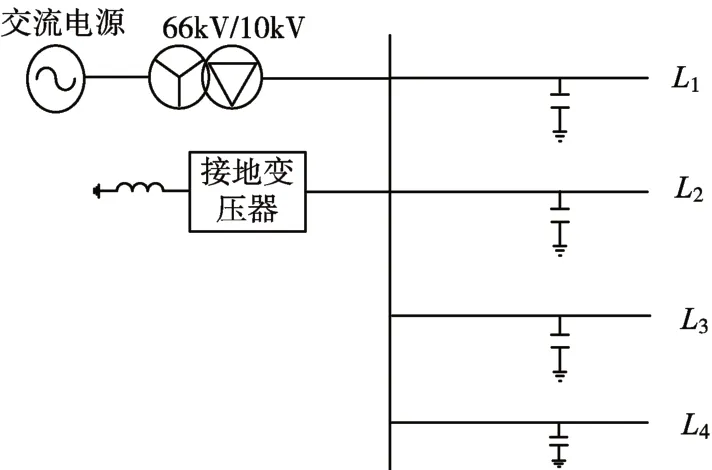
圖1 配電系統仿真模型

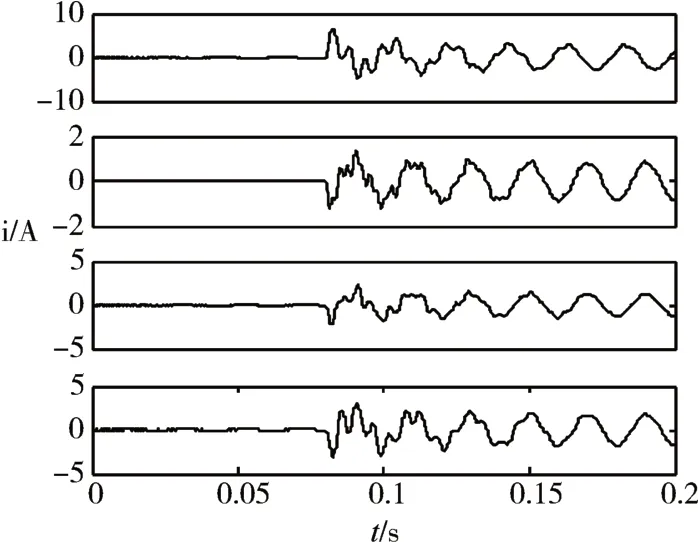
圖2 障后各線路零序電流

圖2是故障后各線路零序電流，線路1為故障線路，可以看出線路1零序電流的極性與其余線路相反，且線路1零序電流幅值為其余線路零序電流之和。用EEMD算法對各線路零序信號分解如圖3所示。

圖3是各個線路零序電流EEMD分解的結果，可以看出分解的結果逐漸的變平滑，選取IMF4、IMF5疊加各線路的特征量，計算各線路固有模態函數的多尺度排列熵，所得結果如圖4所示。

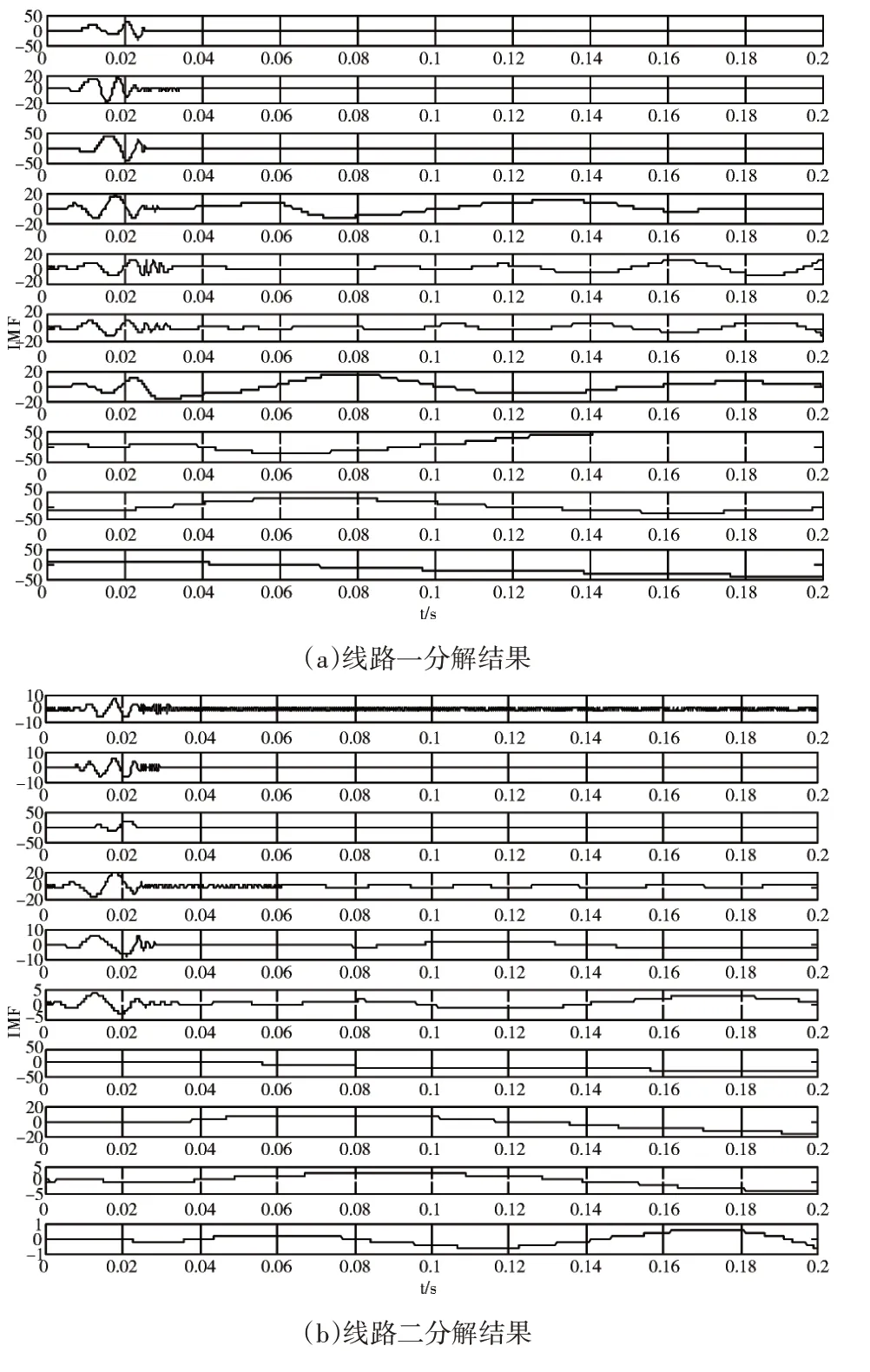
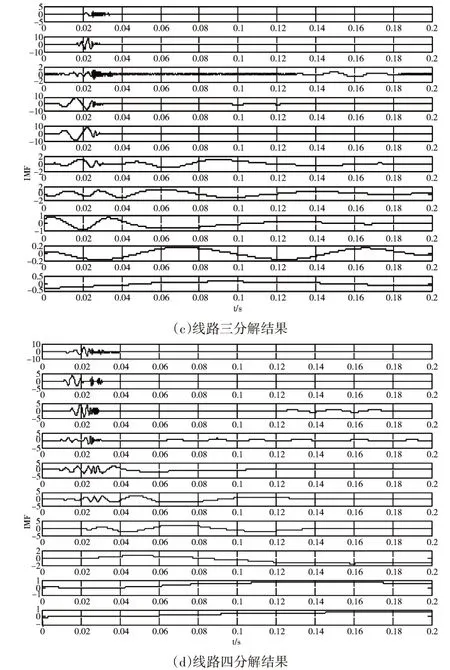
圖3 EEMD分解結果

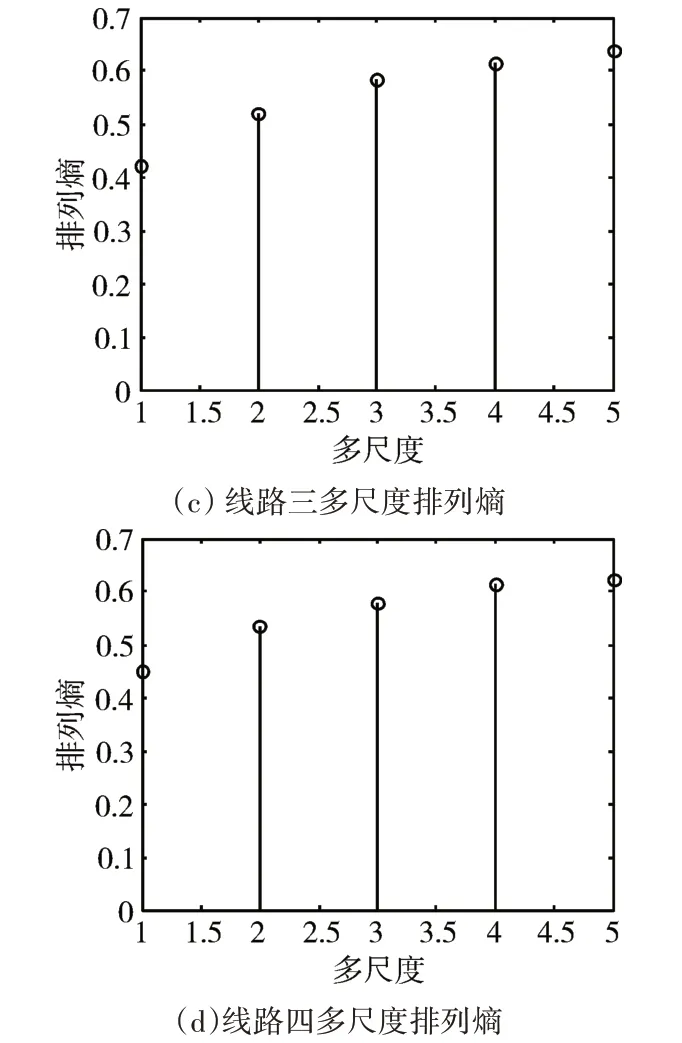
圖4 各線路多尺度排列熵

采用遺傳算法優化SVM對所提取得多尺度排列熵進行分類，對樣本進行分類標簽，其中故障線路設為1，正常線路設為2。

將圖4的多尺度排列熵輸入到已經訓練好的GA-SVM中。其中遺傳算法的種群規模取為100，迭代300次，交叉概率為0.6，變異概率為0.3。算法從線路1到線路4的輸出結果分別為1，2，2，2。則線路一為故障線路，與初始設置的故障線路一致。

因為實際中高阻接地情況較為普遍，補充1000Ω接地實驗。

圖5是高阻接地故障后各線路零序電流，線路1為故障線路，可以看出線路1零序電流的極性與其余線路相反，且線路1零序電流幅值為其余線路零序電流之和。用EEMD算法對各線路零序信號分解如圖6所示。

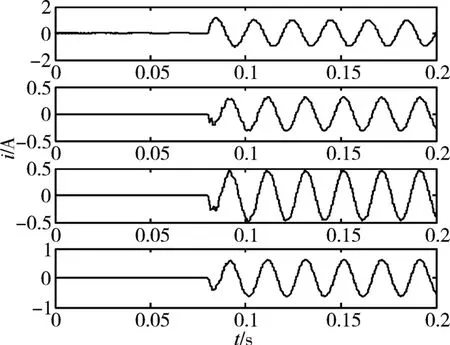
圖5 故障后各線路零序電流

圖6是各個線路零序電流EEMD分解的結果，可以看出分解的結果逐漸的變平滑，選取IMF4、IMF5疊加作為各線路的特征量，計算各線路第一固有模態函數的多尺度排列熵，所得結果如圖7所示。

圖6 EMD分解結果

圖7 線路多尺度排列熵

采用遺傳算法優化SVM對所提取得多尺度排列熵進行分類，輸出結果分別為1、2、2、2。則線路一為故障線路，與初始設置的故障線路一致。

故障線路、合閘時間、短路距離的不同對選線結果都會產生影響，為此都進行了仿真實驗，結果如表1所示，從表中可以看出，本文所提出的選線方法并沒有出現錯選或者漏選，對故障選線有較高的可靠性。

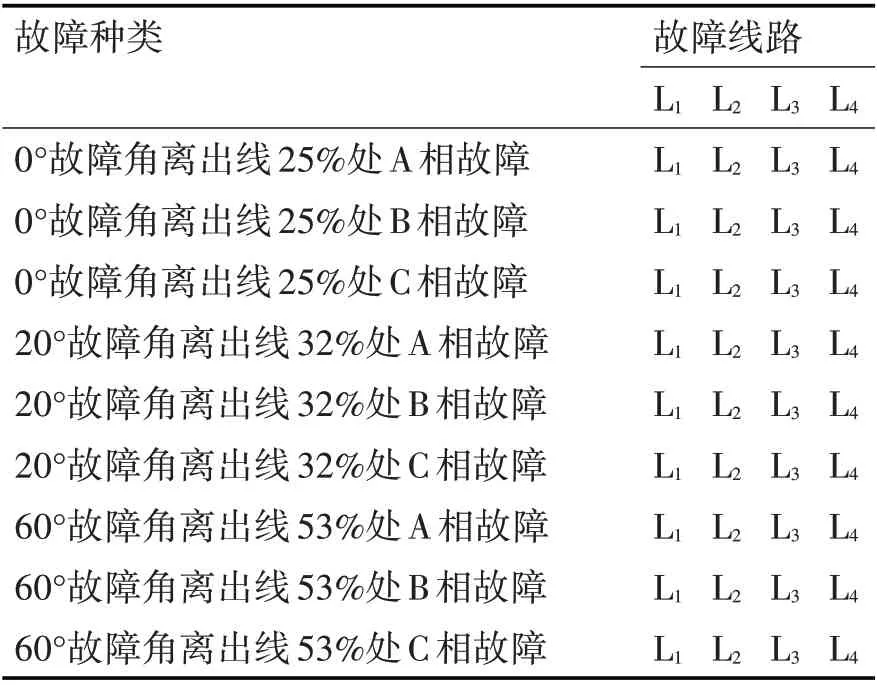
表1 同情況故障選線

6 結語

結合了EEMD-多尺度排列熵-SVM算法完成了小電流系統單相接地故障選線，EEMD算法抑制了模態混淆問題，消除了零序電流的噪聲和干擾，通過計算多尺度排列熵，得到SVM的輸入，通過SVM輸出的標簽作為故障判據完成故障選線，經仿真實驗表明方法準確、簡單，沒有出現誤判。