一種可信任的大容量無載體信息隱藏方案

杜耀剛 楊自力 張艷碩 王澤豪

1(北京電子科技學院 北京 100070)

2(西安電子科技大學通信工程學院 陜西 西安 710071)

3(數據通信科學技術研究所 北京 100191)

0 引 言

信息隱藏技術[1-3]分為嵌入式信息隱藏技術[4-5]和無載體信息隱藏技術[6-8]。無載體信息隱藏技術的研究領域主要有基于文本[9-10]和基于圖像兩個方向。目前在圖像方面進行的無載體信息隱藏方案，大多數集中在如何利用圖像的特征變化規律來進行信息的隱藏設計。如將圖像進行3×3分塊，然后通過每塊像素值按一定規則進行比較產生秘密比特信息[11]；又或者將圖像分塊之后通過比較子塊像素值變化方向來產生秘密比特信息[12]。這其中存在許多問題，如信息隱藏圖像在傳輸過程中受到攻擊或者刻意篡改，那么接收方就會提取出錯誤的秘密信息。同時這些方案每幅圖像只能與固定的隱秘信息進行對應，如果要傳輸大量秘密信息則需要大量的圖像，這就將產生不小的存儲負擔。而且這些方案的隱藏容量相對較低，還有很大的提升空間。

針對以上問題，本文提出了一種既能驗證圖像完整性，同時減少系統存儲資源消耗并且有很高隱藏容量的無載體信息隱藏方案。該方案是基于線性碼[13]的生成矩陣和校驗矩陣思想結合混沌映射理論以及迭代線性方程組[14]設計的無載體信息隱藏系統。方案通過提取圖像的像素值，然后經過設計的系統的一系列變換來確定圖像與密文信息的對應規則。信息發送方和接收方分別通過無載體信息隱藏系統可確定需要發送的圖像信息和接收的密文信息。該方案創新性地將混沌加密算法嵌入到線性碼理論中形成一種新的信息隱藏算法，使得信息在隱藏過程中具有混沌加密算法的隨機性和安全性，同時具有線性碼的可驗證性。另外與圖像對應的秘密信息在算法的實現過程中形成了相比于其他算法容量大的特點，并且由于兩者之間的動態關聯性，大大減少了信息庫的存儲資源消耗。

1 線性碼原理

圖像在傳遞的過程中可能會遭受到攻擊方刻意的篡改或者數據缺失，這樣就會導致接收方解密出錯誤的信息。為了避免出現這種情況，方案利用線性碼的可驗證性對信息進行認證。

現有一個有限域Fq，若q=pn，其中p為素數。則稱其n維向量空間為Qn，也記作Rn。

定義1若C是一個[n,k]線性碼，則C也一定是有限域Fq上的n維線性空間Rn中的一個k維線性子空間。

定義2一個k×n矩陣G,其行向量構成的基底若能經過線性組合表示[n,k]線性碼C中的任何碼字即：

C={aG|a∈Qk}

則稱矩陣G為線性碼C的生成矩陣。若G=(Ik,P)是標準型的矩陣,即Ik是k×k的單位矩陣,則每個碼字的前k個符號用來表示信息位,后面的n-k個符號用來表示校驗位。

定義3若C是一個[n,k]線性碼,那么其對偶碼C⊥為:

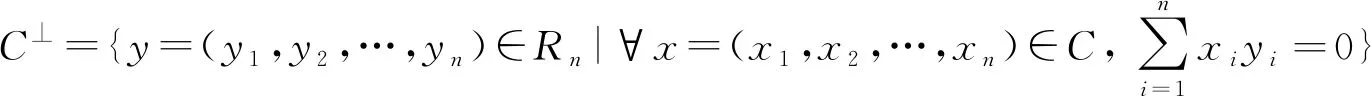
2 混沌映射理論

混沌系統是指在一個確定性系統中，存在隨機的不規則的運動，其行為表現為不確定性、不可重復性、不可預測性，這就是混沌現象。針對這種現象產生了多種混沌映射系統：一維Logistic映射、二維Henon映射、三維Lorenz映射等。本文采用的是一維Logistic混沌映射[15]對信息進行加密。

Logistic混沌映射從數學形式上看是一種相對簡單的混沌系統，但卻具有極其復雜的動力學行為，在選定合適的初始條件下，產生的混沌序列是非周期的、不收斂的、無法預測的。其數學表達式如下：

xk+1=μxk(1-xk)

(1)

式中：μ為系統參數，根據輸出需求可以確定對應的k值，0<μ≤4，xk∈(0，1)。如果初始參數發生變化，那么對應的混沌序列也會跟著發生變化，且這種變化是無規律的。因此，確保了加密系統的安全性。本文方案初始參數x0取值為0.5，通信雙方通過協商之后在3.57≤μ≤4之間選取一樣的μ值來輸出混沌序列。

3 無載體信息隱藏簡介

無載體信息隱藏的提出是針對傳統的嵌入式信息隱藏難以抵抗發展迅速的各類隱寫分析算法[16-18]的檢測。而難以抵抗檢測的根本原因是嵌入式的信息隱藏方式改變了載體信息，雖然嵌入方式是采用載體信息的冗余度進行的，可以讓人無法通過感官系統察覺出來，但是卻逃不過隱寫分析算法的檢測。

無載體信息隱藏技術依然需要載體進行信息的傳輸，與以往的信息隱藏方式不同的是，它沒有改變載體信息，而是利用載體本身具有的特征按照一定的規則來構成與秘密信息的對應聯系，以此來達到傳輸秘密信息的目的。當然，為了增加安全性會對特征信息進行量化加密處理。無載體信息隱藏技術利用的傳輸載體是原始的、未作改變的，因此不會引起攻擊者的懷疑，也不會被各類隱寫分析算法檢測出來。由于具有出眾的保密通信優勢，這項技術受到了大量專家的重視。

4 無載體信息隱藏方案

本節給出了所提的具體無載體信息隱藏實現方案，該方案是通過對選取的圖像進行像素值的處理，得到對應的像素矩陣，然后對像素值的二進制矩陣利用線性碼的校驗原理作可驗證運算，之后對生成的矩陣信息與經過混沌加密的參數矩陣一起構建迭代線性方程組，然后利用經過迭代線性方程組變換得到的矩陣信息與公開的矩陣信息一起得到最終傳輸的隱秘信息，最后利用坐標信息即可在信息庫中找到相應的密文信息。發送方通過以上方案的步驟得到密文信息與圖像的對應關系，然后根據要傳輸的密文信息找到對應的圖像進行發送，接收方接收到圖像之后，根據方案的步驟進行處理就可得到對應的隱秘矩陣信息，進而得到密文信息，并可對信息的完整性進行驗證。方案的具體步驟先后分為圖像處理、參數生成與發送、信息提取和完整性驗證四部分。

4.1 圖像處理

一幅灰度圖像，可由r0×s0個像素pij(1≤i≤r0,1≤j≤s0)所構成，因此可以將圖像用一個矩陣M來表示, 其中pij為圖像的組成像素值。

設有m幅傳輸圖像，其對應的像素矩陣為r0×s0的矩陣Mi(i=1,2,…,m)。本文的任務即將這m個傳輸圖像提取像素值通過矩陣生成算法用m個矩陣來表示。

4.2 參數生成與發送

步驟1按照線性碼理論隨機生成一個s0×n0的標準型生成矩陣G(Gij∈[0,1])，對矩陣Mi(i=1,2,…,m)，按式(2)計算對應的Si(i=1,2,…,m)。

Si=MiGi=1,2,…,m

(2)

此時根據生成矩陣G的校驗位矩陣提取出對應在Si(i=1,2,…,m)上的驗證矩陣Ji(i=1,2,…,m)，根據定義2可知驗證矩陣Ji(i=1,2,…,m)為Si(i=1,2,…,m)的后面n-k列形成的矩陣。

Mi來自于圖像的像素值作模二運算生成的二進制矩陣，本方案選用的生成矩陣G是標準型的矩陣，能最后對圖像的完整性進行有效的檢驗。

步驟2根據需求設置n個初始未經加密的參數矩陣Bi(i=1,2,…,n)和選定初始值μ之后由式(1)產生混沌序列進而轉化的混沌矩陣L，對參數矩陣Bi(i=1,2,…,n)按式(3)得到加密參數矩陣Ci(i=1,2,…,n)。

Ci=Bi⊕Li=1,2，…，n

(3)

定義如下矩陣序列：

S1,S2，…，Sm,C1,C2，…，Cn,D0,D1，…，Dn+m

其中，Di(i=0,1,…,n+m)是通過在它之前的n+m個矩陣進行運算而得到。即：

(4)

步驟3根據需要設置矩陣Ti(i=1,2,…,N)，其中1≤N≤m+n，然后計算Ki(i=1,2,…,N)：

Ki=Di-Tii=1，2，…，N

(5)

合并Ki(i=1,2,…,N)得到映射矩陣Yi(i=1,2,…,N)，找出密文信息在映射矩陣上對應的坐標信息Zi(i=1,2,…,N)，即可實現無載體信息隱藏。

步驟4將信息G,Bi(i=1,2,…,n),Ji(i=1,2,…,m),Ti(i=1,2,…,N),Zi(i=1,2,…,N)公開。混沌加密系數μ通過可靠信道傳送給接收方。

4.3 信息提取

秘密接收方接收到圖像之后對圖像進行解析生成矩陣Mi(i=1,2,…,m)，由式(2)和公開的生成矩陣G，可計算得Si(i=1,2,…,m)。再由得到的混沌加密系數μ得到混沌矩陣L，由公開的Bi(i=1,2,…,n)按式(3)得到加密參數矩陣Ci(i=1,2,…,n)，結合式(4),可將S1,S2，…，Sm,C1,C2，…，Cn轉化為：

(D0,D1,…，Dn+m)T=Q(S1,S2，…，Sm,C1,C2，…，Cn)T

(6)

式中：系數a通過式(4)合并同類項得到。此刻也就能解出Di(i=0,1,…,n+m)。最后通過公開的矩陣Ti(i=1,2,…,N)，結合式(5)，可計算出秘密矩陣Ki(i=1,2,…,N)，之后變換得到映射矩陣Yi(i=1,2,…,N)，由坐標信息Zi(i=1,2,…,N)即可找到在信息庫中對應的密文信息。

4.4 完整性驗證

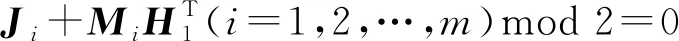
5 方案實現

本文選取的三幅實驗圖像——lena、baboon、airplane均為512×512灰度圖像，如圖1所示。

圖1 實驗用圖

5.1 發送方

將lena、baboon、airplane三幅實驗用圖的像素調整為8×8之后，其像素矩陣分別如圖2所示。

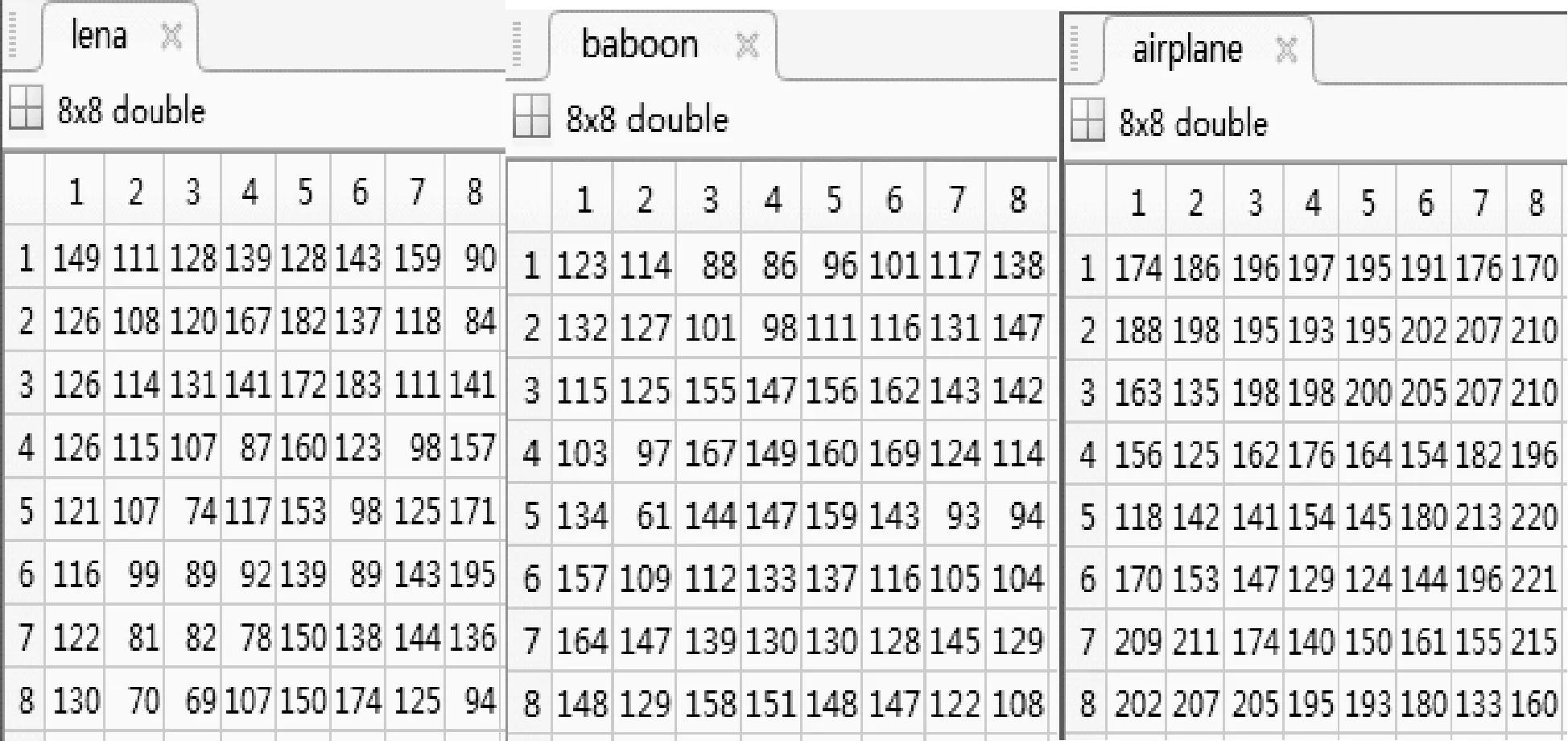
圖2 lena,baboon,airplane像素矩陣(8×8)

對以上像素矩陣值模2取余生成二進制矩陣Mi(i=1,2,3)分別如圖3所示。

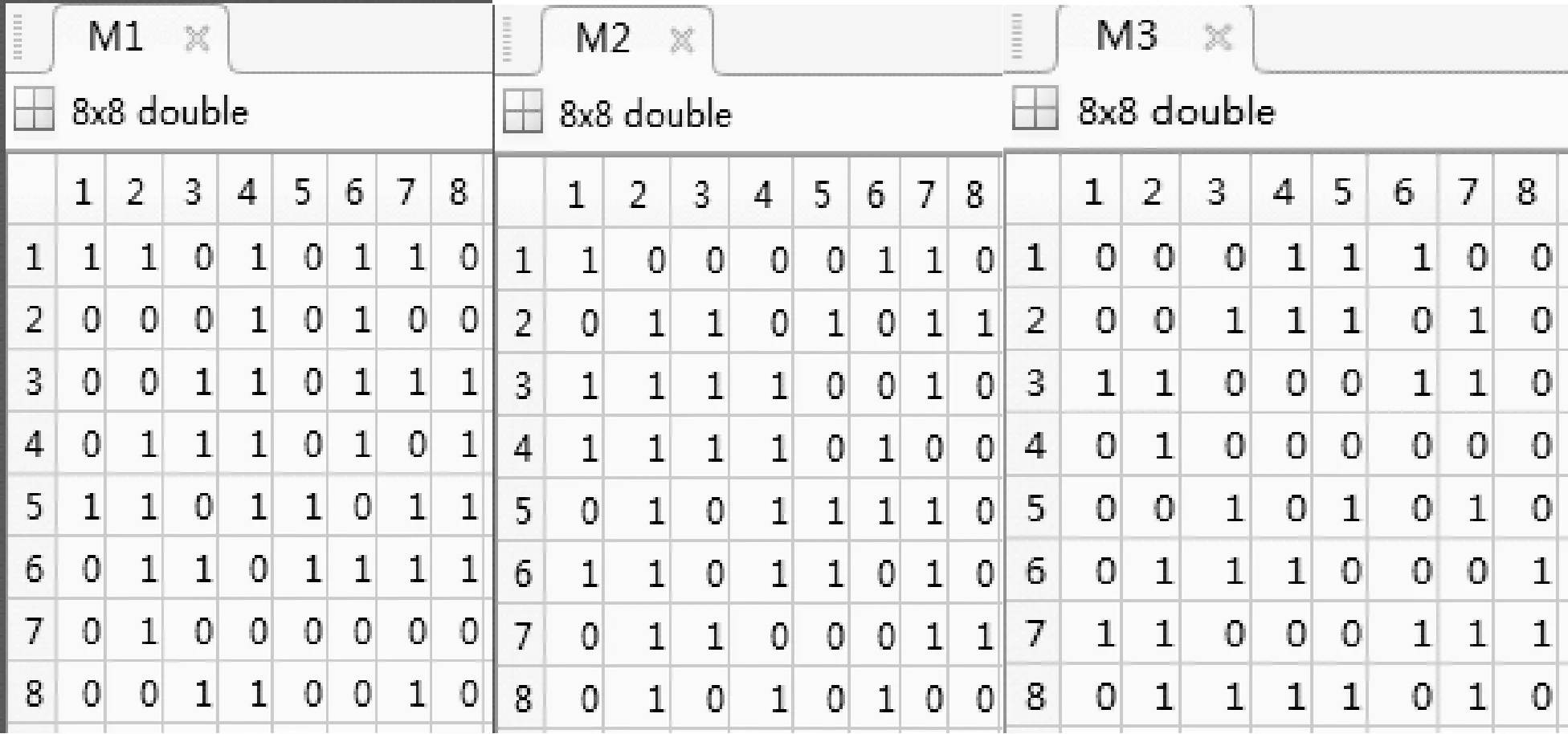
圖3 lena,baboon,airplane二進制矩陣(8×8)

然后構造一個標準型生成矩陣G(8×9)，如圖4所示。

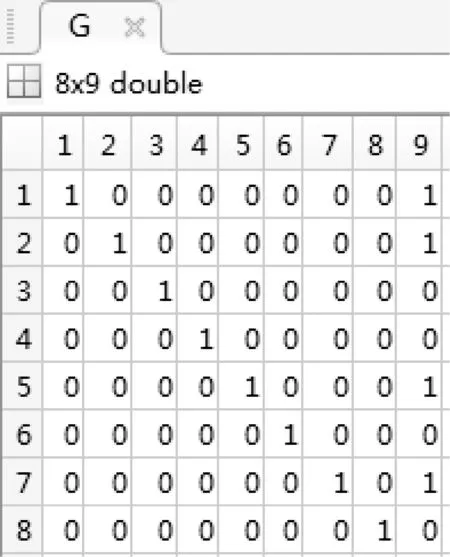
圖4 生成矩陣G(8×9)

由式(2)可得Si(i=1,2,3)如圖5所示。

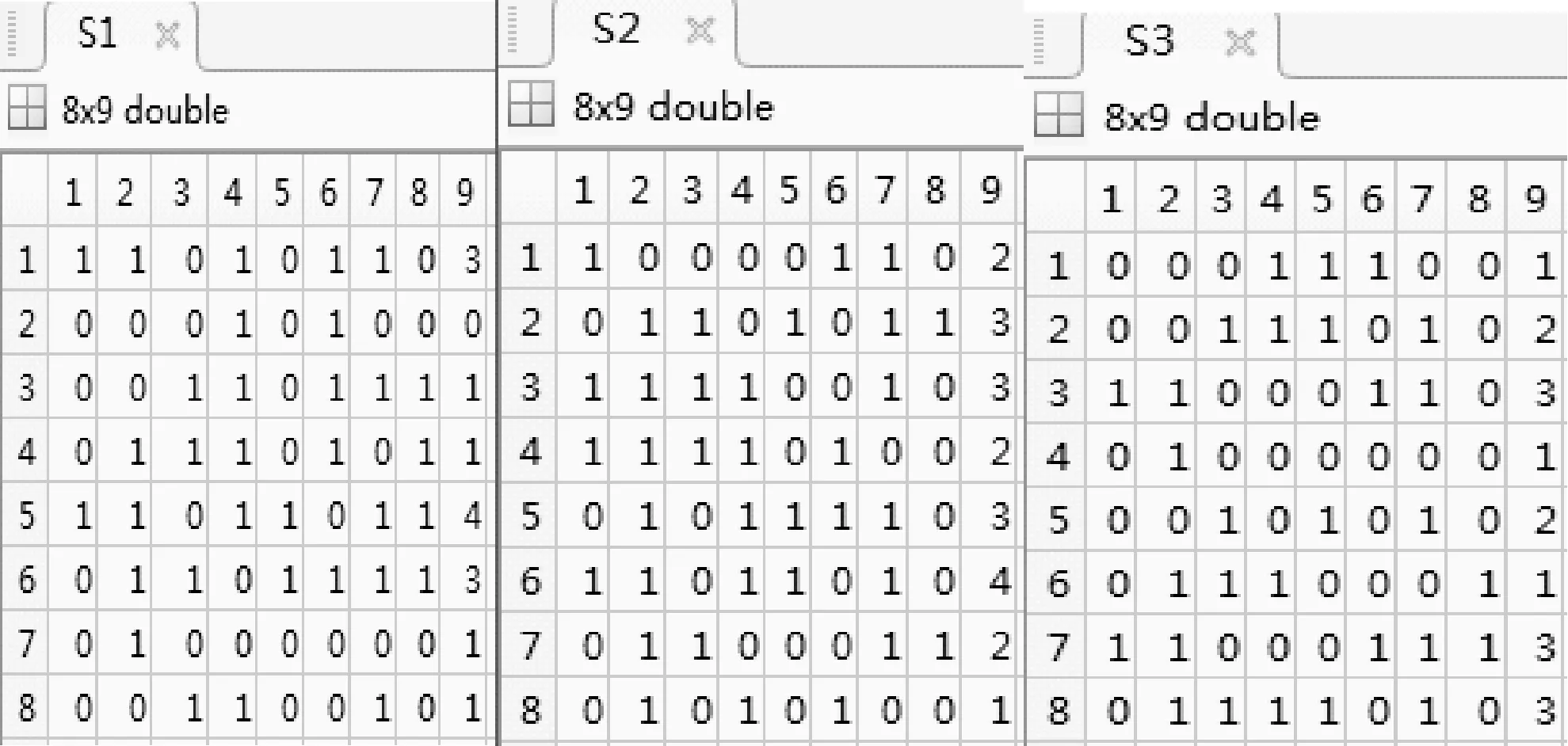
圖5 矩陣Si(i=1,2,3)(8×9)

由于傳送的圖像為3幅，因此，設置矩陣Bi(i=1,2)，如圖6所示。

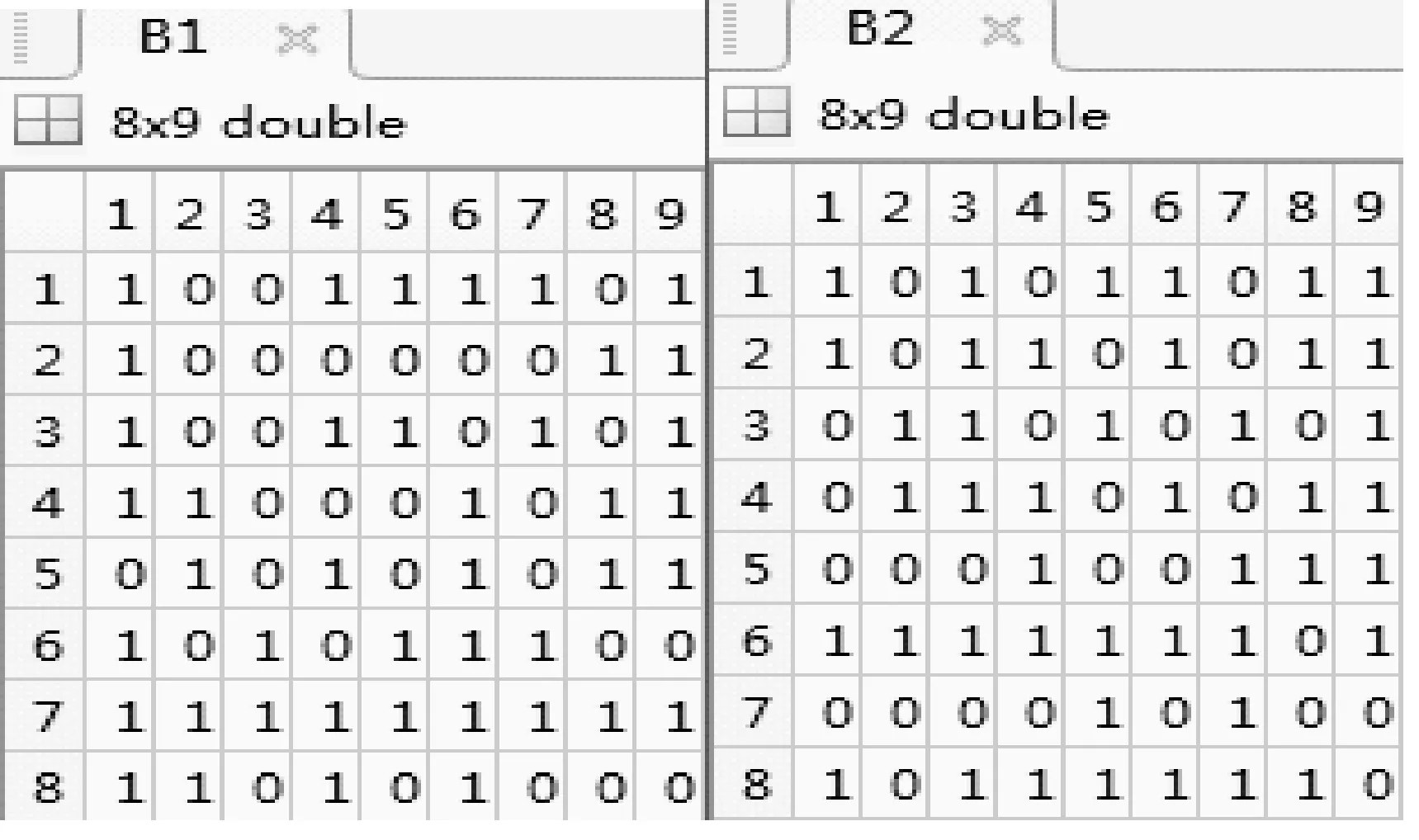
圖6 矩陣B1,B2(8×9)

根據傳輸的μ值取3.8和式(1)可得到對應的混沌序列轉化的混沌矩陣L如圖7所示。

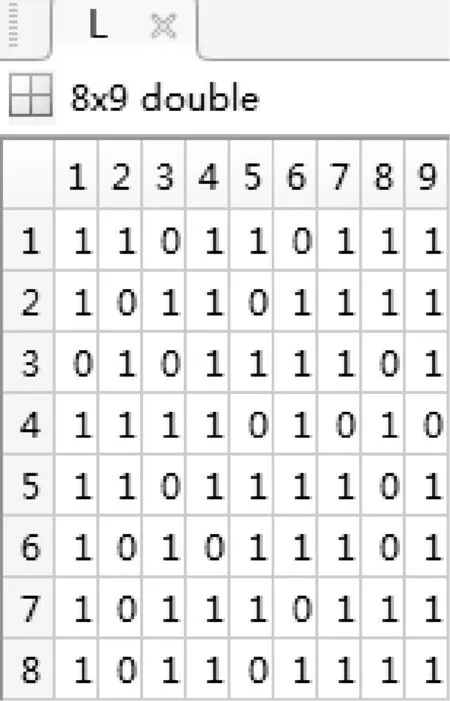
圖7 矩陣L(8×9)

根據Bi(i=1,2)，混沌矩陣L和式(3)，可求得參數矩陣Ci(i=1,2)如圖8所示。

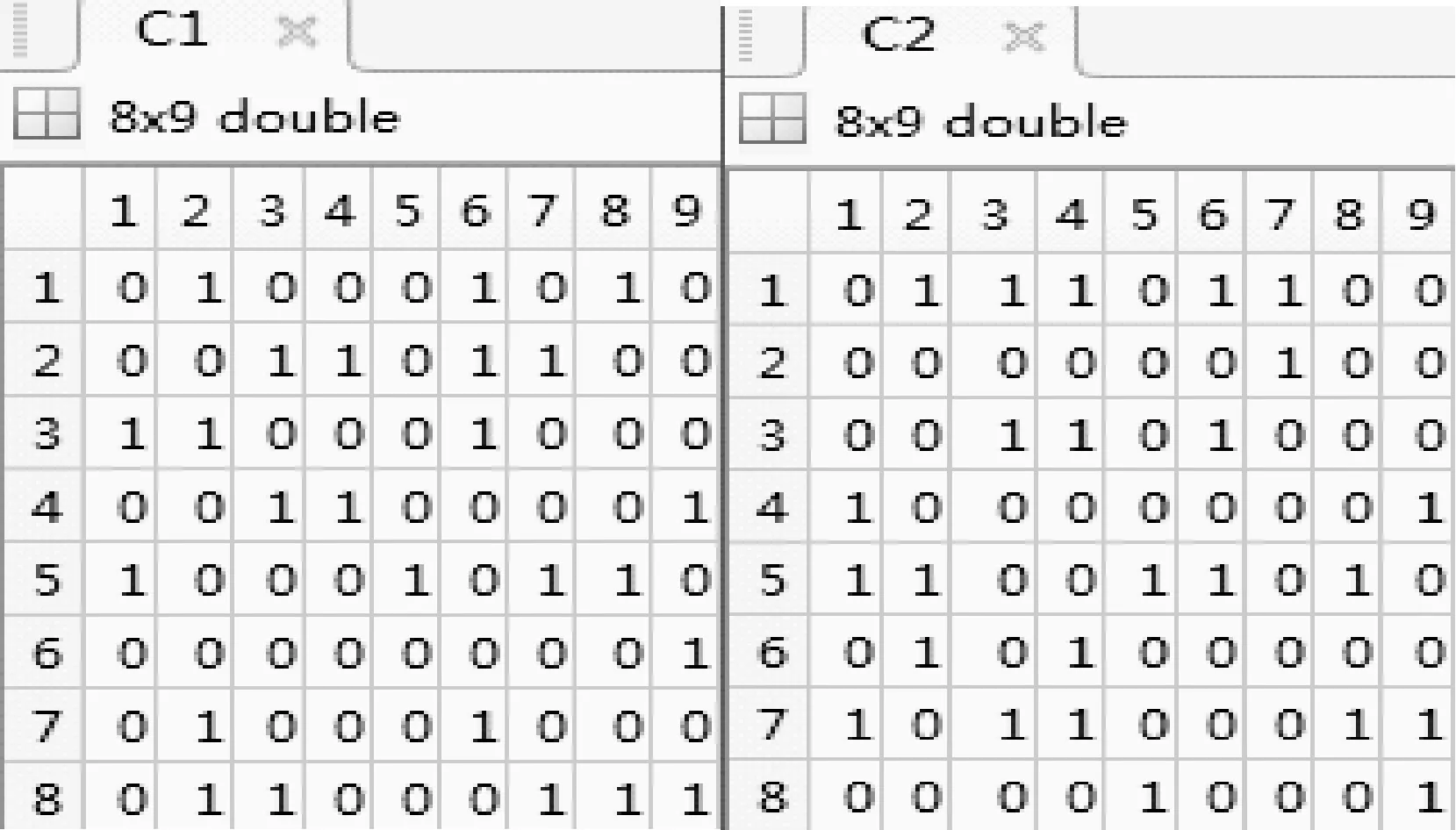
圖8 矩陣C1,C2(8×9)

根據Si(i=1,2,3)、Ci(i=1,2)和式(4),可求得Di(i=0,1,…,5)如圖9所示。

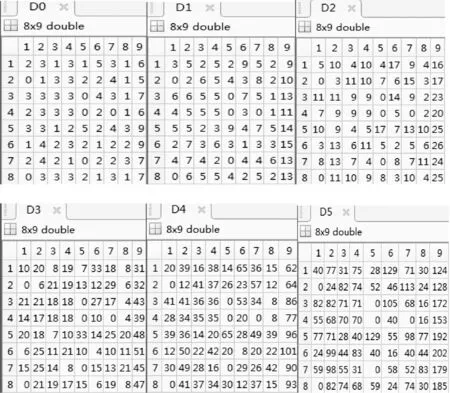
圖9 矩陣Di(i=0,1,…,5)(8×9)

設置生成兩個8×9矩陣T1、T2如圖10所示。

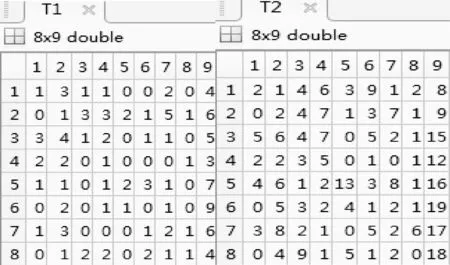
圖10 矩陣T1,T2(8×9)

由式(5)可得K1、K2如圖11所示。

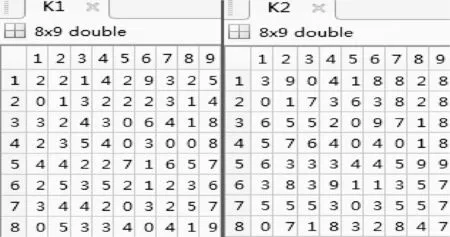
圖11 矩陣K1,K2(8×9)

將矩陣K1、K2每三位信息合并生成映射矩陣信息Y1、Y2如圖12所示。

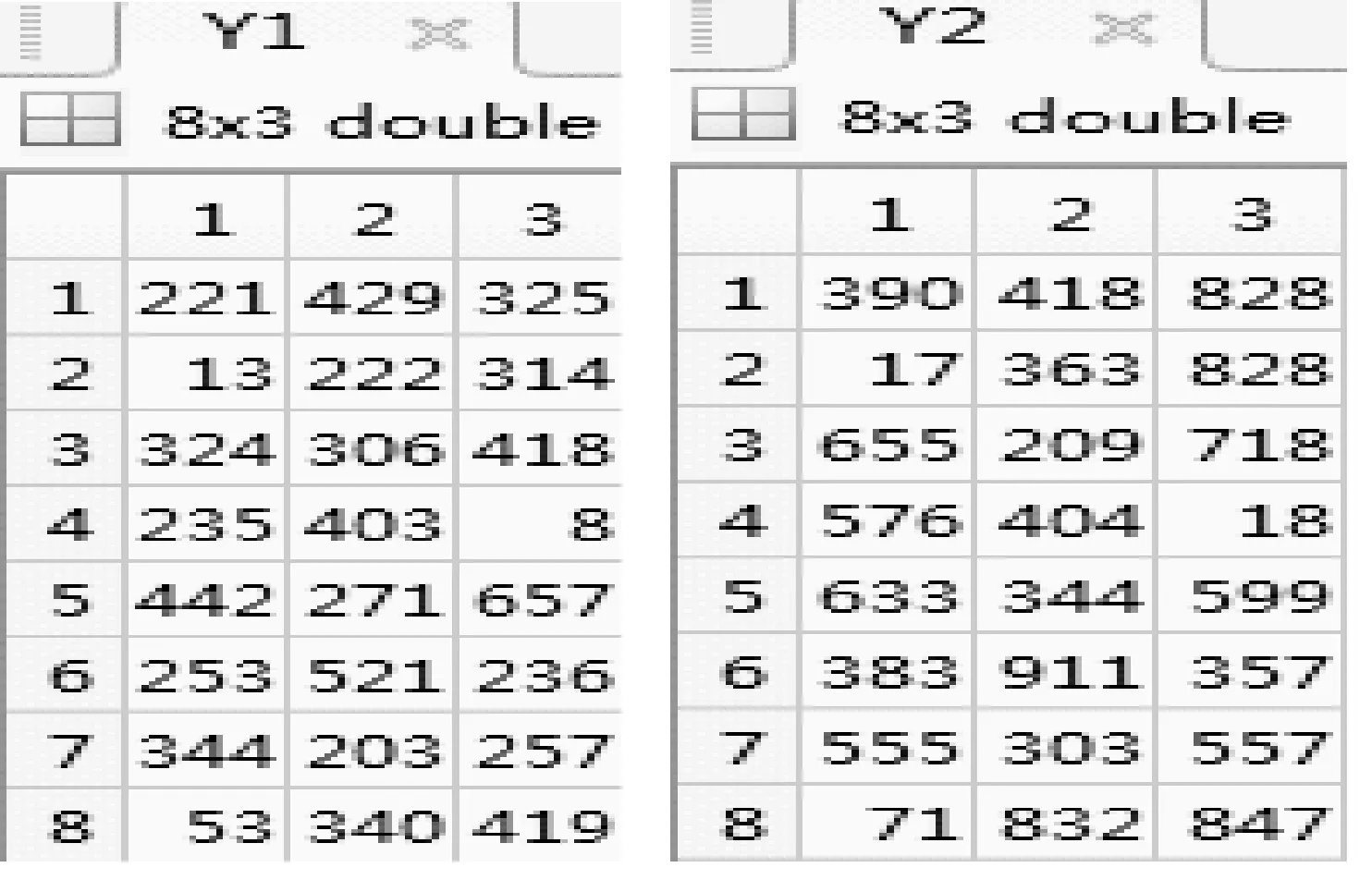
圖12 矩陣Y1,Y2(8×3)

若傳輸的信息為“北京”，而信息庫的對應關系為“北”?“013”，“,京”?“018”，則找到在矩陣中對應的坐標信息Z1=(2,1),Z2=(4,3)，至此，公開G、T1、T2、B1、B2、Z1、Z2,然后將圖像發送給信息接收方，混沌系數μ通過可靠信道傳輸，信息發送的步驟完成。

5.2 接收方

秘密接收方接收到圖像之后對圖像進行解析生成矩陣Mi(i=1,2,…,m),由式(2)和公開的生成矩陣G，可計算得Si(i=1,2,…,m)。再由接收到的混沌加密系數μ通過混沌映射變換由公開的Bi(i=1,2,…,m)也就能計算得到Ci(i=1,2,…,n)，結合式(4),這時本文可以解出Di(i=0,1,…,n+m)。最后通過公開的Ti(i=1,2,…,N)，結合式(5)，可計算出加密矩陣Ki(i=1,2,…,N),然后可對應得到映射矩陣Yi(i=1,2,…,N),根據得到的坐標信息Zi(i=1,2,…,N)，參照信息庫即可得到傳輸的密文信息如圖13所示。

圖13 密文信息

信息完整性驗證，由于生成矩陣G為標準型矩陣G=(Ik,P)，因此在本方案中其校驗矩陣為：

H1=[11001010]

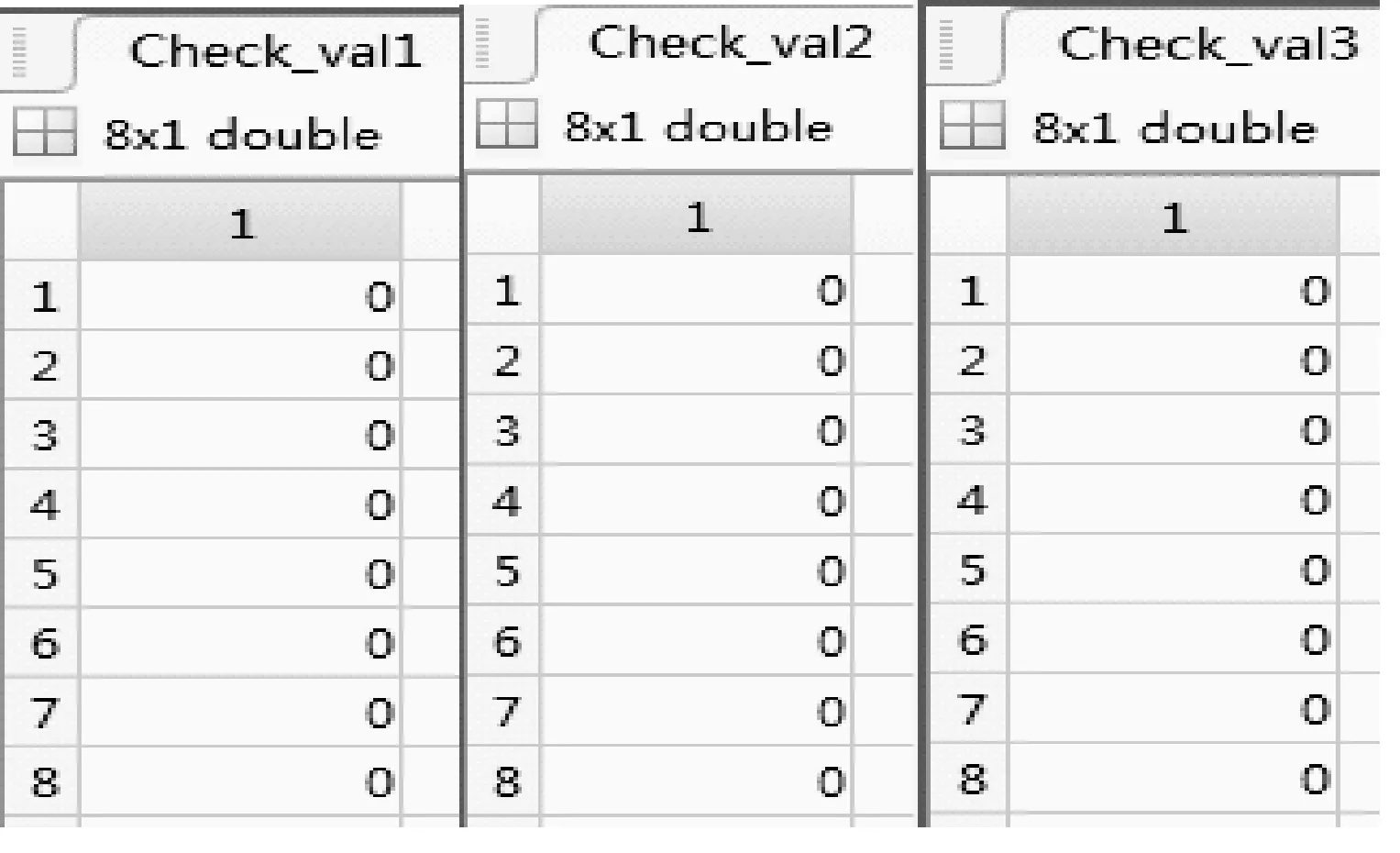
圖14 Mi(i=1,2,3)校驗結果正確

假設由于傳輸過程中圖像遭到信息的篡改或破壞，進而導致Mi(i=1,2,3) 中一個或多個出現變動，例如圖像lena信息被篡改導致M1中出現錯誤，如圖15所示。

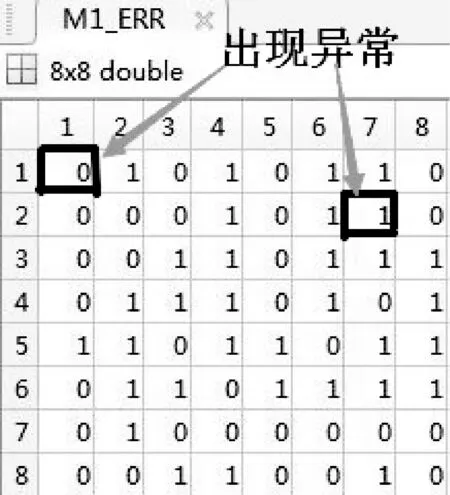
圖15 M1黑框中數據出現錯誤

那么，J1+M1HTmod 2后得到的校驗結果就不再是0，可以判斷接收數據出現錯誤，如圖16所示。

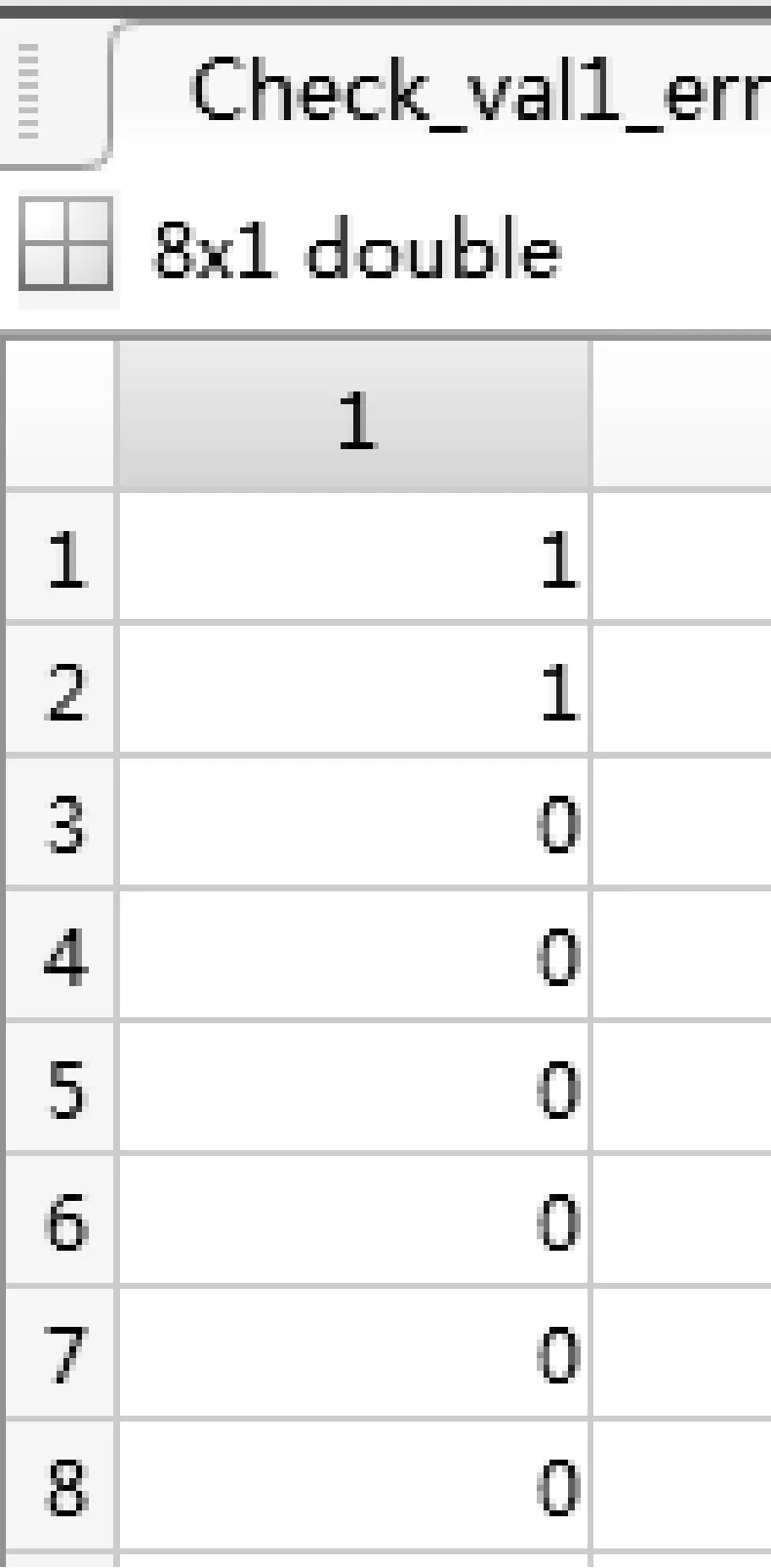
圖16 錯誤的M1導致錯誤的校驗值

6 方案特性分析

6.1 隱藏容量分析

該方案是通過對3幅圖像進行像素值處理，得到對應的3個像素矩陣，然后對像素矩陣利用線性碼的校驗原理作可驗證處理。之后對生成的矩陣信息與經過混沌加密的參數矩陣一起構建迭代線性方程組，利用迭代線性方程組得到的矩陣信息與公開的矩陣信息一起獲得最終要傳輸的隱秘矩陣信息，然后根據矩陣的坐標信息找到與信息庫對應的密文信息。方案采用的是利用3幅圖像進行傳輸，最終解密出2個秘密信息矩陣的形式進行信息的傳輸。另外本方案的圖像分割方式是采用8×8的像素值矩陣進行，為了便于與其他方案進行對比，本文采用3×3的形式進行計算。故解密出的信息矩陣形式是3×4，由于十進制信息矩陣每個值代表3比特的二進制信息，因此平均每幅圖片最后可表示的比特值信息是:

3×4×3×2÷3=24 bit

與其他方案對比信息如表1所示。

表1 隱藏容量對比

由表1對比可知，本文方案相比于其他兩種方案在隱藏容量上有了較大的提高，隱藏容量是文獻[11]方案的四倍，比文獻[12]方案隱藏容量提升三分之一。

6.2 可驗證性分析

為了防止秘密信息在傳遞過程中遭遇毀壞或篡改而導致接收方無法察覺進而解密出錯誤信息，本文設計了一個可信任的無載體信息隱藏方案，需要根據線性碼理論中的生成碼和校驗碼的思想，在解密信息的過程中加入生成矩陣和校驗矩陣進行完整性的驗證，驗證步驟如下：

步驟1通過信息發送方公開的生成矩陣G，根據定義3可得到對應的校驗矩陣H1。

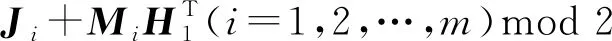
表2 可驗證性對比

6.3 安全性分析

該方案在信息的加解密的過程中引入了迭代線性方程組的形式使得信息被解密的難度加大，同時將混沌映射加密系統嵌入到加解密過程中，使得系統具有了混沌映射的隨機性、混沌特性,攻擊方無法找出其中的輸入輸出關系，若攻擊方無法得到正確的混沌加密系數，則根本進行不了解密操作，故本文方案具有很強的安全性。

6.4 存儲資源消耗分析

本文方案由于將圖像的像素值矩陣作為加解密信息的一環，與設置的混沌加密矩陣Ci(i=1,2,…,n)一起導出最終的秘密信息矩陣。同一幅圖像，與不同的參數矩陣Ci(i=1,2,…,n)將對應的是不同的秘密信息矩陣，故圖像與秘密信息矩陣是動態關聯的。一幅圖像將可以表示大量的隱秘信息，而傳統無載體信息隱藏系統，圖像與隱秘信息是一對一的關系。因此本文方案能大大減少無載體信息隱藏系統的存儲資源消耗。

7 結 語

本文提出了一種利用線性碼的生成矩陣和校驗矩陣思想結合迭代方程組以及混沌映射加密設計的無載體信息隱藏方案。該方案能在接收方收到圖像信息之后對圖像信息的完整性進行驗證，避免提取出錯誤的信息。而一般的無載體信息方案則無法抵抗來自攻擊方對信息的無差別攻擊引起的解密誤差。并且方案采用了迭代方程組以及混沌映射系統結合的方式，使得系統的安全性和隨機性很高。因此這是一個可信任的無載體信息隱藏方案，同時該方案有著很大的隱藏容量提升，隱藏容量是文獻[11]方案的四倍，相比文獻[12]方案提升三分之一。并且方案的圖像信息與密文信息是動態關聯的關系，大大減少了系統的存儲資源消耗。